| Autor |
Nachricht |
TomW
Gast
|
 TomW Verfasst am: 13. Feb 2014 16:21 Titel: Schwarzes Loch |
 |
|
Meine Frage:
Meine Frage dreht sich um die Schwarzen Löcher.
Kann es sein, dass es die eigentlich gar nicht gibt?!
Ich stelle mir vor, ich stehe auf der Erde und beobachte, wie ein riesiger Stern kollabiert. Er zieht sich immer weiter zusammen und sein Radius nähert sich dem Schwarzschildradius an... aber gleichzeitig steigt auch die Zeitdehnung immer weiter an, ich sehe also durch mein Teleskop, wie sich das Zusammenziehen immer weiter verlangsamt und verlangsamt.
Am Ereignishorizont (= Schwarzschildradius) selbst wäre die Zeitdilatation unendlich groß - die Zeit steht still. Folglich nähert sich der Sternradius aus meiner (Erden-)Sicht asymptotisch dem Schwarzschildradius an, erreicht ihn aber erst nach unendlich langer Zeit - auf gut Deutsch, nie.
Mit anderen Worten: Die Dinger, die wir immer als "Schwarze Löcher" bezeichnen (inklusive Ereignishorizont, der keine wirkliche Grenze ist, Vakuum im Inneren und einer punktförmigen Singularität), sind in Wirklichkeit nur kollabierende Sterne, die bis in alle Ewigkeit kurz davor stehen, Schwarze Löcher (mit obigen Eigenschaften) zu werden, diesen Zustand aber nie erreichen können.
Macht das Sinn?
Meine Ideen:
Einerseits klingt das zwar logisch, aber dafür, dass das Innere von Schwarzen Löchern immer so emsig diskutiert wird, scheint mir ein rein theoretisches Gebilde ein bisschen zu wenig als Gegenstand solcher Diskussionen.
Irgendwo habe ich gelesen, dass hineinfallende Körper den Schwarzschildradius durch ihre Masse zu sich ziehen und somit in endlicher Zeit verschluckt werden... aber das bezog sich auf sehr große Massen (z.B. Sterne).
Oder hat es etwas damit zu tun, dass ein Gravitationsfeld rein theoretisch unendliche Reichweite hat und sich somit der Erdbeobachter ebenfalls darin befindet (folglich auch solchen Effekten wie der Zeitdilatation ausgeliefert ist)?
Ich hoffe, jemand weiß, wo hier mein Denkfehler liegt... schon mal danke im Voraus!
|
|
 |
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18088
|
| TomS Verfasst am: 13. Feb 2014 17:57 Titel: |
|
|
Aus Sicht eines weit genug außen stehenden, stationären Beobachters verhält es sich so wie du sagst. Aber für den mit hineinfallenden Beobacher entsteht der Horizont in endlicher Eigenzeit, und der hineinfallenden Beobachter erreicht wiederum in endlicher Zeit die sich bildende Singularität.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5044
|
| DrStupid Verfasst am: 13. Feb 2014 18:17 Titel: Re: Schwarzes Loch |
|
|
| TomW hat Folgendes geschrieben: | | Am Ereignishorizont (= Schwarzschildradius) selbst wäre die Zeitdilatation unendlich groß - die Zeit steht still. Folglich nähert sich der Sternradius aus meiner (Erden-)Sicht asymptotisch dem Schwarzschildradius an, erreicht ihn aber erst nach unendlich langer Zeit - auf gut Deutsch, nie. |
Dein Fehler besteht darin, dass Du den Ereignishorizont als statisch ansiehst. Tatsächlich dehnt er sich aufgrund der hineinfallenden Masse aber aus und verschluckt sie auch für einen außenstehenden Beobachter in endlicher Zeit.
Richtig ist Deine Argumentation aber für die Singularität. Die kann sich aufgrund der immer größer werdenden Zeitdilatation tatsächlich nicht bilden. Wenn ein in das Loch fallender Beobachter auf wundersame Weise überleben könnte, würde er das Zentrum nie erreichen und sich statt dessen irgendwann im leeren Raum wiederfinden, weil das Loch verdampft ist.
|
|
|
Günther
Anmeldungsdatum: 23.11.2010
Beiträge: 305
|
| Günther Verfasst am: 13. Feb 2014 18:50 Titel: Re: Schwarzes Loch |
|
|
| DrStupid hat Folgendes geschrieben: |
Richtig ist Deine Argumentation aber für die Singularität. Die kann sich aufgrund der immer größer werdenden Zeitdilatation tatsächlich nicht bilden. Wenn ein in das Loch fallender Beobachter auf wundersame Weise überleben könnte, würde er das Zentrum nie erreichen und sich statt dessen irgendwann im leeren Raum wiederfinden, weil das Loch verdampft ist. |
Wirklich? In Koordinatenzeit klebt der Freifaller am Horizont, in seiner Eigenzeit erreicht er relativ schnell die Singularität, wie TomS schon geschrieben hat.
|
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5044
|
| DrStupid Verfasst am: 13. Feb 2014 19:02 Titel: Re: Schwarzes Loch |
|
|
| Günther hat Folgendes geschrieben: | | In Koordinatenzeit klebt der Freifaller am Horizont |
Nur wenn der Horizont statisch wäre. Das ist er aber nicht wenn die Masse des Schwarzen Loches wächst.
| Günther hat Folgendes geschrieben: | | in seiner Eigenzeit erreicht er relativ schnell die Singularität, wie TomS schon geschrieben hat. |
Das Loch verdampft aber noch schneller.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18088
|
| TomS Verfasst am: 13. Feb 2014 19:20 Titel: Re: Schwarzes Loch |
|
|
| DrStupid hat Folgendes geschrieben: | | TomW hat Folgendes geschrieben: | | Am Ereignishorizont (= Schwarzschildradius) selbst wäre die Zeitdilatation unendlich groß - die Zeit steht still. Folglich nähert sich der Sternradius aus meiner (Erden-)Sicht asymptotisch dem Schwarzschildradius an, erreicht ihn aber erst nach unendlich langer Zeit - auf gut Deutsch, nie. |
Dein Fehler besteht darin, dass Du den Ereignishorizont als statisch ansiehst. Tatsächlich dehnt er sich aufgrund der hineinfallenden Masse aber aus und verschluckt sie auch für einen außenstehenden Beobachter in endlicher Zeit. |
Das ist ja nicht unbedingt ein Fehler. Wenn keine weitere Materie hineinfällt (den Beobachter ausgenommen) dann ist der Horizont nach Bildung statisch, so wie die gesamte Raumzeit außerhalb des Horizontes.
| DrStupid hat Folgendes geschrieben: | | Günther hat Folgendes geschrieben: | | in seiner Eigenzeit erreicht er relativ schnell die Singularität, wie TomS schon geschrieben hat. |
Das Loch verdampft aber noch schneller. |
Man kann das ja explizit berechnen. Der freie Fall ins schwarze Loch kann z.B. einige Stunden Tage dauern, das Verdampfen länger als das Alter des Universums. Der Beobachter erreicht also die Singularität in endlicher und vergleichsweise kurzer Eigenzeit.
Ich reiche Beispiele nach
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18088
|
| TomS Verfasst am: 13. Feb 2014 19:26 Titel: |
|
|
Wir haben die Rechnung auch hier im Forum schon diskutiert. Allerdings ist der folgende Link doch noch besser: Theoretische Physik: Relativitätstheorie und Kosmologie
Die Eigenzeit für den Fall vom EH zum Zentrum ist also ca. von der Größenordnung der Lichtlaufzeit.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 13. Feb 2014 19:31, insgesamt einmal bearbeitet |
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5044
|
| DrStupid Verfasst am: 13. Feb 2014 19:30 Titel: Re: Schwarzes Loch |
|
|
| TomS hat Folgendes geschrieben: | | Wenn keine weitere Materie hineinfällt |
Dann hätten wir keinen Gravitationskollaps.
| DrStupid hat Folgendes geschrieben: | | Der freie Fall ins schwarze Loch kann z.B. einige Stunden Tage dauern, das Verdampfen länger als das Alter des Universums. |
In jeweils welchem Bezugssystem?
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18088
|
| TomS Verfasst am: 13. Feb 2014 19:39 Titel: Re: Schwarzes Loch |
|
|
| DrStupid hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Wenn keine weitere Materie hineinfällt |
Dann hätten wir keinen Gravitationskollaps. |
Doch. Ein isolierter genügend größer Stern gibt Materie und Strahlung ab und schrumpft dabei. Ab einem bestimmten Zeitpunkt, wenn genügend Materie innerhalb des Schwarzschildradius enthalten ist, bildet sich der Ereignishorizont. Die noch außerhalb befindliche Materie wird zumindest teilweise ebenfalls den EH überqueren (der dabei wächst) und ins SL fallen.
Theoretisch ist jedoch ein exakt sphärisch symmetrischer Kollaps denkbar, bei dem sich der EH genau dann bildet, wenn die gesamte Materie den Schwarzschildradius gerade überschritten hat. Dann wäre der EH ab seiner Bildung statisch.
Aber auch im allgemeinen Fall wäre der EH im ansonsten leeren Raum statisch.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5044
|
| DrStupid Verfasst am: 13. Feb 2014 19:54 Titel: Re: Schwarzes Loch |
|
|
| TomS hat Folgendes geschrieben: | | Die noch außerhalb befindliche Materie wird zumindest teilweise ebenfalls den EH überqueren (der dabei wächst) und ins SL fallen. |
Genau darum geht es hier. TomW war der Meinung, dass diese Materie den EH aus Sicht eines außenstehenden Beobachters erst nach unendlich langer Zeit erreicht. Tatsächlich schafft sie es aber in endlicher Zeit, weil der EH ihr entgegen kommt.
| TomS hat Folgendes geschrieben: | | Theoretisch ist jedoch ein exakt sphärisch symmetrischer Kollaps denkbar, bei dem sich der EH genau dann bildet, wenn die gesamte Materie den Schwarzschildradius gerade überschritten hat. Dann wäre der EH ab seiner Bildung statisch. |
Hier geht es darum, was während des Kollaps pasiert und nicht danach. Während des Kollaps kann man den EH auch in diesem Fall schwerlich als statisch bezeichnen. Bis kurz vor Schluss existiert er gar nicht und dann ist er plötzlich da. Dynamischer geht es gar nicht.
| TomS hat Folgendes geschrieben: | | Aber auch im allgemeinen Fall wäre der EH im ansonsten leeren Raum statisch. |
Darum geht es hier aber nicht.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18088
|
| TomS Verfasst am: 13. Feb 2014 20:09 Titel: |
|
|
Du kannst dich ja als Beobachter auf die Oberfläche der kollabierenden Materie setzen und mit ihr zusammen ins sich bildende SL stürzen (nehmen wir der Einfachheit halber an, dass es sich um eine Kugel aus drucklosem Staub handelt, der im freien Fall kollabiert).
Die Oberfläche erreicht den sich bildenden EH in endlicher (sehr kurzer) Zeit, und für den weiteren Kollaps gilt das oben gesagt.
Da sich die Materie vollständig innerhalb einer kollabierenden Kugelschale befindet, mit der du frei fällst, findet der Kollaps in einer (im Außenraum) statischen Raumzeit statt. Und du bemerkst das Auftreten des EHs nicht, egal ob er schon existiert wenn du ihn überquerst oder ob er sich in dem Moment bildet, in dem du ihn überquerst.
Die einzige Dynamik besteht darin, dass die Außenraumlösung sozusagen nach innen wächst, während die Innenraumlösung schrumpft. Aber für den frei fallenden Beobachter ist das Auftreten bzw. Entstehen des Horizontes in nichts von einer statischen Raumzeit zu unterscheiden.
Anyway: der freie Fall geht flott, das Verdampfen nicht ;-)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5044
|
| DrStupid Verfasst am: 13. Feb 2014 20:54 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | Du kannst dich ja als Beobachter auf die Oberfläche der kollabierenden Materie setzen und mit ihr zusammen ins sich bildende SL stürzen |
Ja, das kann man machen, aber es ging ausdrücklich um die Beschreibung aus Sicht eines außenstehenden Beobachters.
| TomS hat Folgendes geschrieben: | | Anyway: der freie Fall geht flott, das Verdampfen nicht ;-) |
Da Du die Frage oben nicht beantwortet hast, stelle ich sie hier nochmal: Aus wessen Sicht?
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18088
|
| TomS Verfasst am: 13. Feb 2014 23:02 Titel: |
|
|
Nun der freie Fall wie gesagt in der Eigenzeit des frei fallenden Beobachters.
Das Verdampfen zunächst natürlich aus der Sicht des stationären, außenstehenden Beobachters (die Berechnungen werden üblicherweise für den asymptotischen Beobachter im Unendlichen durchgeführt, aber sie gelten mit der üblichen Korrektur der gravitativen Zeitdilatation auch für einen Beobachter bei endlichem Radius).
Ich weiß, was jetzt dein Argument sein wird: damit ist noch nichts über den frei fallenden Beobachter innerhalb des EH gesagt. Da hast du zunächst recht, ich denke aber, mir fällt noch ein Argument ein, dass auch dieser nicht vor dem Erreichen der Singularität das "Verdampfen" erlebt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomW
Gast
|
| TomW Verfasst am: 14. Feb 2014 15:31 Titel: |
|
|
Vielleicht muss ich das noch einmal klarer formulieren:
Es geht mir NICHT darum, was ein in das Loch fallender Beobachter erlebt.
Es geht mir NICHT darum, mit welcher Geschwindigkeit ein Steinbrocken in das Loch fällt, oder was der Ereignishorizont tut, sondern darum, wie der Ereignishorizont aus Sicht des Erdenbewohners überhaupt entstehen kann, wenn es doch aufgrund der Zeitdehnung unendlich lange dauern müsste, bis die Sternoberfläche ihn unterschreitet.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18088
|
| TomS Verfasst am: 14. Feb 2014 15:57 Titel: |
|
|
Gut.
Also zunächst mal noch eine Bemerkung zu DrStupid: mir tatsächlich nicht klar, wie man zeigen kann, dass ein innerhalb des EHs gefangener Beobachter die Singularität erreicht, bevor das SL vollständig verdampft. Gründe:
1) ich kenne keine semiklassische Lösung der ART für "dM/dt < 0 plus Strahlung" (die bekannten SL-Lösungen gehen ja von dM/dt = 0 aus)
2) ich kenne erst recht keine semiklassische Lösung für dieses Szenario, die den Innenraum mit einschließt
3) zu lösen wäre die Geodätengleichung des Beobachters d.h. sein x(s), sowie die Lösung für den Horizont d.h. R(t), jeweils in geeigneten Koordinaten; zu zeigen wäre, ob x(s) den Horizont bei R(t) schneidet oder nicht; ohne (2) ist das nicht lösbar
4) ich finde kein Argument, das ohne diese mathematische Betrachtung auskommt
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18088
|
| TomS Verfasst am: 14. Feb 2014 15:59 Titel: |
|
|
| TomW hat Folgendes geschrieben: | | Es geht mir ... darum, wie der Ereignishorizont aus Sicht des Erdenbewohners überhaupt entstehen kann, wenn es doch aufgrund der Zeitdehnung unendlich lange dauern müsste, bis die Sternoberfläche ihn unterschreitet. |
Zunächst ist die Definition von „Ereignishorizont“ nicht ganz einfach. Die bekannteste Definition lautet (grob), dass es sich um eine lichtartige, geschlossene Fläche handelt, aus der keine zeit- oder lichtartige Kurve entkommen kann. Vereinfacht gesprochen: Licht kann den EH nie verlassen.
Das Problem ist das Wörtchen „nie“, denn dies bedeutet, dass die Eigenschaft der Raumzeit, einen EH zu enthalten, erst in der unendlich fernen Zukunft festgestellt werden kann. Man muss eben unendlich lange warten, um sicher zu wissen, dass tatsächlich nie etwas herauskommt.
Das bedeutet nun, dass der Horizont als solchen nicht lokal definiert ist. Es gibt keine Vorschrift, was ein Beobachter in der Nähe oder am EH tun sollte (messen sollte), um herauszufinden, dass ein EH vorliegt. D.h. auch dass dein | TomW hat Folgendes geschrieben: | | aus Sicht des Erdenbewohnes |
extrem problematisch ist.
Die theoretischen Physiker haben sich ein neues Konzept überlegt, das des sogenannten „isolierten Horizontes“ IH, das eine formal korrekte Beschreibung von „Licht kann den IH nie verlassen“ liefert, die am IH selbst anwendbar ist. Das bedeutet, wir können dein Problem wohl so umformulieren:
„Es geht mir darum, wie aus Sicht eines außenstehenden Beobachters eine Raumregion entstehen kann, wenn es doch aufgrund der Zeitdilatation (aus Sicht eines außenstehenden Beobachters) unendlich lange dauern müsste, bis die kollabierende Materie vollständig in dieser Raumregion enthalten ist.“
Die einfachste Lösung der ART, die einen Gravitationskollaps mit Horizont beschreibt, ist der sogenannte Oppenheimer-Snyder-Kollaps. Hier handelt es sich um eine endliche Kugel aus drucklosem Staub, der radial und freien fallend ins Zentrum stürzt. Im Außenraum der Kugel gilt die Schwarzschild-Lösung (so wie für jede statische, kugelsymmetrische Raumzeit). Ein mit der Oberfläche der Kugel frei mitfallender Beobachter erreicht in endlicher Eigenzeit das Zentrum (dass hinter ihm ein Horizont entsteht merkt er nicht). Die Raumzeit im Außenraum ist statisch, allerdings bewegt sich die Grenzfläche zwischen Außen- und Innenraum d.h. die Kugeloberfläche nach innen. Uns interessiert wie ein außenstehender Beobachter bei festem Radius R diese nach innen stürzende Kugelschale mit Radius r(t), dr/dt < 0 wahrnimmt.
Eine recht gute Darstellung findest du hier in Abbildung 3: http://people.bu.edu/pbokulic/blackholes/
Wir nehmen an, dass der mit fallende Astronaut in regelmäßigen Abständen Lichtblitze von der Oberfläche der kollabierenden Kugel radial nach außen sendet. Zunächst erreichen diese den außenstehenden Beobachter in regelmäßigen Abständen; allerdings werden die Abstände aufgrund der Zeitdilatation immer größer, und die Frequenz des Lichtes wird immer stärker rotverschoben. In dem Moment, wo der Astronaut den sich bildenden Horizont erreicht, (Abb. 3: d.h. wo die durchgezogene die gestrichelte Linie schneidet), werden Rotverschiebung und Zeitdilatation unendlich. Das radial nach außen abgestrahlte Licht bleibt am Horizont gefangen (Abb. 3: d.h. die Lichtstrahlen laufen senkrecht nach oben entsprechend der gestrichelten Linie). Der Horizont ist eine lichtartige Fläche, d.h. radial auslaufende Lichtstrahlen bewegen sich auf dem Horizont.
„aus Sicht eines außenstehenden Beobachters“ scheint das aus dieser Richtung kommende Licht plötzlich zu verschwinden, d.h. es wird im Zuge des Gravitationskollaps eine absolut schwarze, wachsende Scheibe auftreten.
„wie … eine Raumregion entstehen kann, wenn es doch aufgrund der Zeitdilatation … unendlich lange dauern müsste, bis die kollabierende Materie vollständig in dieser Raumregion enthalten ist.“
Der Horizont ist jeweils gerade sie groß, wie durch die im Inneren befindliche Materie definiert. Es liegt ein kontinuierlicher Zufluss an Materie durch den Horizont vor. Der Horizont wächst, weil die Materie in im freien Fall überquert und dadurch zur Masse im Inneren beiträgt. Der Schwarzschildradius ist direkt proportional zur enthaltenen Masse.
Um also zu argumentieren, dass sich das SL tatsächlich bildet, betrachtet man den frei fallenden Staub. Nur um zu berechnen, was der außenstehende Beobachter wahrnimmt, nimmt man dessen Position ein,
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5044
|
| DrStupid Verfasst am: 14. Feb 2014 17:29 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | Also zunächst mal noch eine Bemerkung zu DrStupid: mir tatsächlich nicht klar, wie man zeigen kann, dass ein innerhalb des EHs gefangener Beobachter die Singularität erreicht, bevor das SL vollständig verdampft. |
Versuchen wir es doch mal anders herum: Wie lange dauert der freie Fall aus Sicht eines außenstehenden Beobachters (ohne Berücksichtigung von Signallaufzeiten)? Kann man das halbwegs sinnvoll beantworten?
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18088
|
| TomS Verfasst am: 15. Feb 2014 00:18 Titel: |
|
|
der freie Fall bis zum EH dauert aus Sicht des außenstehenden Beobachters unendlich lange
die Zeit bis zur Verdampfung dauert nur endlich lange; die Schlussfolgerung, dass das SL verdampft, bevor der Astronaut den EH erreicht, ist aber trotzdem falsch
der Astronaut überquert den EH in endlicher Eigenzeit; wenn er genau zu diesem Zeitpunkt ein Lichtsignal radial nach außen schickt, dann verbleibt dieses natürlich am EH, solange dieser existiert; im Moment der vollständigen Zerstrahlung verschwindet der Horizont und das gefangene Lichtsignal - evtl. mit dem Photo des Astronauten - wird zeitgleich mit dem letzten Lichtblitz der Hawkingstrahlung wieder sichtbar; der außenstehende Beobachter sieht also in sehr ferner Zukunft den Astronaut im Moment des Überquerens des EHs zusammen mit allen anderen Lichtsignalen einfallender Objekte seit der Bildung des EH; das Innere des EHs bleibt natürlich weiterhin unbeobachtbar; das Argument gilt natürlich nur, wenn der Astronaut nicht zu spät startet bzw. wenn das SL groß genug ist
d.h. aber nur, dass meine Argumentation zwar beweist, dass der Astronaut trotz Hawkingstrahlung den EH überquert und dass dies entgegen des Szenarios ohne Hawkingstrahlung tatsächlich sichtbar wird; es heißt jedoch noch nicht, dass der Astronaut nach der Überquerung des EH auch die Singularität vor der Zerstrahlung erreicht
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5044
|
| DrStupid Verfasst am: 15. Feb 2014 00:39 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | der freie Fall bis zum EH dauert aus Sicht des außenstehenden Beobachters unendlich lange |
Ich glaube wir reden aneinander vorbei. Ich spreche vom der Erreichen der Singularität im Zentrum des Schwarzen Loches. Das Erreichen und Überqueren des EH steht außer Frage. Wenn man die Ausdehnung des EH berücksichtigt, geschieht das für den außenstehenden Beobachter sogar in endlicher Zeit.
| TomS hat Folgendes geschrieben: | | die Zeit bis zur Verdampfung dauert nur endlich lange; die Schlussfolgerung, dass das SL verdampft, bevor der Astronaut den EH erreicht, ist aber trotzdem falsch |
Ich versuche es zu verstehen, aber es gelingt mir nicht. Wie soll der Astronaut irgend etwas erreichen (egal was), wenn er dazu länger braucht, als es existiert?
| TomS hat Folgendes geschrieben: | | der Astronaut überquert den EH in endlicher Eigenzeit; wenn er genau zu diesem Zeitpunkt ein Lichtsignal radial nach außen schickt, dann verbleibt dieses natürlich am EH, solange dieser existiert; im Moment der vollständigen Zerstrahlung verschwindet der Horizont und das gefangene Lichtsignal - evtl. mit dem Photo des Astronauten - wird zeitgleich mit dem letzten Lichtblitz der Hawkingstrahlung wieder sichtbar; |
Warum erst dann? Wandert es mit dem schrumpfenden Horizont nach innen?
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18088
|
| TomS Verfasst am: 15. Feb 2014 01:10 Titel: |
|
|
| DrStupid hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | der freie Fall bis zum EH dauert aus Sicht des außenstehenden Beobachters unendlich lange |
Ich glaube wir reden aneinander vorbei. Ich spreche vom der Erreichen der Singularität im Zentrum des Schwarzen Loches. |
Du kannst keine für den Außenstehenden gültige Zeitkoordinate angeben. Ich kenne jedenfalls keine Koordinaten, die am EH regulär sind und (!) die eine übliche Zeitkoordinate enthalten, d.h. deren Metrik bzgl. Raum und Zeit diagonal sind.
Schau mal hier, evtl. findet sich da was.
http://en.wikipedia.org/wiki/Eddington%E2%80%93Finkelstein_coordinates
| DrStupid hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | die Zeit bis zur Verdampfung dauert nur endlich lange; die Schlussfolgerung, dass das SL verdampft, bevor der Astronaut den EH erreicht, ist aber trotzdem falsch |
Ich versuche es zu verstehen, aber es gelingt mir nicht. Wie soll der Astronaut irgend etwas erreichen (egal was), wenn er dazu länger braucht, als es existiert? |
Es geht nicht ums Erreichen (das wird mittels Eigenzeit diskutiert, sondern um das Sehen des Erreichens. Meine Erklärung findest so oder so ähnlich bestimmt auch im Internet. Was ist denn daran unklar?
| DrStupid hat Folgendes geschrieben: | Ich | TomS hat Folgendes geschrieben: | | der Astronaut überquert den EH in endlicher Eigenzeit; wenn er genau zu diesem Zeitpunkt ein Lichtsignal radial nach außen schickt, dann verbleibt dieses natürlich am EH, solange dieser existiert; im Moment der vollständigen Zerstrahlung verschwindet der Horizont und das gefangene Lichtsignal - evtl. mit dem Photo des Astronauten - wird zeitgleich mit dem letzten Lichtblitz der Hawkingstrahlung wieder sichtbar; |
Warum erst dann? Wandert es mit dem schrumpfenden Horizont nach innen? |
Ja, sozusagen. Der Horizont ist eine lichtartige Fläche. Er "besteht" genau aus den radial nach außen laufenden lichtartigen Geodäten. D.h. dass ein Lichtsignal, das direkt am EH radial nach außen abgestrahlt wird, am EH verbleibt (das besagen auch die gekippten Lichtkegel in den bekannten Graphiken)
Die ganze Diskussion leidet natürlich darunter, dass man für die Metrik keine exakte Lösung hat. Ich habe inzwischen eine semiklassische Näherung gefunden, aber sie sieht extrem kompliziert aus.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomW
Gast
|
| TomW Verfasst am: 15. Feb 2014 08:19 Titel: |
|
|
Also...
| Zitat: | | Es gibt keine Vorschrift, was ein Beobachter in der Nähe oder am EH tun sollte (messen sollte), um herauszufinden, dass ein EH vorliegt. |
Wenn ein Astrophysiker sagt, wir haben an der Stelle abc ein Schwarzes Loch gefunden, außerdem an der Stelle def und an der Stelle ghi (was ja wohl heißt, dass man einen Ereignishorizont (=schwarzen Fleck) oder die Auswirkungen starker Gravitation gefunden hat), dann ist es das, was ich mit Schwarzes Loch bzw Ereignishorizont meine.
In deinem Link steht auch ein interessanter Absatz, der meine Frage gut beschreibt:
| Zitat: | Notice that the matter never crosses the event horizon, regardless of how long one waits, and thus one might be inclined to think that a "true" black hole will never have time to form. For this reason, early researchers in general relativity thought that we needn't be concerned about black hole singularities, and they referred these collapsed objects as "frozen stars" (see Thorne et al. 1986).
However, we now know that this picture is too limited. |
Eine verständliche Erklärung habe ich aber auch nicht gefunden...
Das Beispiel mit den Lichtstrahlen übernehme ich jetzt einfach mal. Ich stelle mir vor, auf der Oberfläche des Sterns strahlt eine Lichtquelle nach außen, und der weit entfernte Beobachter untersucht diese Lichtwellen. Beim Zusammensturz werden die Wellen immer stärker rotverschoben, da sich die Sternoberfläche asymptotisch dem Schwarzschildradius (also der Position des theoretischen EHs) annähert. Die Wellenlänge steigt und steigt, und auch die Maßzahl z für die Rotverschiebung - aber damit das Licht verschwinden würde, müsste z unendlich groß werden - was aber erst nach unendlich langer Zeit geschehen kann, ebenso wie das Erreichen des Schwarzschildradius. Ich kann mir also nicht vorstellen, warum dann diese Lichtwellen auf einen Schlag abbrechen sollten.
| Zitat: | | In dem Moment, wo der Astronaut den sich bildenden Horizont erreicht |
aber meine These ist ja, dass er ihn gar nicht erreichen kann!
| Zitat: | der freie Fall bis zum EH dauert aus Sicht des außenstehenden Beobachters unendlich lange
die Zeit bis zur Verdampfung dauert nur endlich lange; die Schlussfolgerung, dass das SL verdampft, bevor der Astronaut den EH erreicht, ist aber trotzdem falsch |
Den Satz verstehe ich ehrlich gesagt nicht.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18088
|
| TomS Verfasst am: 15. Feb 2014 09:29 Titel: |
|
|
| TomW hat Folgendes geschrieben: | | Zitat: | | Es gibt keine Vorschrift, was ein Beobachter in der Nähe oder am EH tun sollte (messen sollte), um herauszufinden, dass ein EH vorliegt. |
Wenn ein Astrophysiker sagt, wir haben an der Stelle abc ein Schwarzes Loch gefunden, außerdem an der Stelle def und an der Stelle ghi (was ja wohl heißt, dass man einen Ereignishorizont (=schwarzen Fleck) oder die Auswirkungen starker Gravitation gefunden hat), dann ist es das, was ich mit Schwarzes Loch bzw Ereignishorizont meine. |
Ist schon OK. Mir ging es nur darum, dass weder der Astrophysiker noch du eine Möglichkeit hat, durch irgendein lokales Experiment festzustellen, dass "hier und jetzt" ein Horizont vorliegt. Das spielt aber für das folgende kaum eine Rolle.
| TomW hat Folgendes geschrieben: | | Zitat: | | In dem Moment, wo der Astronaut den sich bildenden Horizont erreicht |
aber meine These ist ja, dass er ihn gar nicht erreichen kann! |
Schau dir doch mal das Raumzeit-Diagramm in dem Link an. Du kannst weitere Linien wie die "collapsing matter" zeichnen und mit "free-falling astronauts" beschriften. Du siehst für jede Linie, wie sie den EH schneidet. Man kann berechnen, dass wenn der Astronaut aus endlicher Höhe fällt, dass für ihn eine endliche Eigenzeit vergeht (bis zum EH sowie bis zum Zentrum). Also erreicht und überquert er aus seiner Sicht den EH. Und das ist zunächst, was zählt.
Nun kann man zwei weitere Betrachtungsweisen einführen.
Man kann den Fall des Astronauten in einem Koordinatensystem beschreiben, in dem die Zeitkoordinate der Eigenzeit eines Außenstehenden entspricht. Gemessen in dieser Zeit erreicht der Astronaut den Horizont in unendlich/endlich ferner Zukunft, wenn man das Problem ohne/mit Hawkingstrahlung analysiert.
Die letzte Perspektive wäre die Beobachtung des von Astronauten ausgesandten Lichtes durch einen Außenstehenden. Das Licht erreicht den Außenstehenden in unendlich/endlich ferner Zukunft (die obige Zeitkoordinate plus die Lichtlaufzeit), wiederum wenn man das Problem ohne/mit Hawkingstrahlung analysiert.
| TomW hat Folgendes geschrieben: | | Zitat: | der freie Fall bis zum EH dauert aus Sicht des außenstehenden Beobachters unendlich lange
die Zeit bis zur Verdampfung dauert nur endlich lange; die Schlussfolgerung, dass das SL verdampft, bevor der Astronaut den EH erreicht, ist aber trotzdem falsch |
Den Satz verstehe ich ehrlich gesagt nicht. |
Der Satz beschreibt das Paradoxon, das sich ergibt, wenn man die beiden Szenarien ohne / mit Hawkingstrahlung unzulässig kombiniert. Die Lösung ohne Hawkingstrahlung ist klar: der Astronaut erreicht den EH (aus Sicht des Außenstehenden) in unendlich ferner Zukunft, das SL existiert unendlich lange. Die Lösung mit Hawkingstrahlung hatte ich dann im Folgenden beschrieben: die Lösung lautet: der Astronaut erreicht den EH (aus Sicht des Außenstehenden) in endlich ferner Zukunft, sein Bild beim Überqueren des EHs wird zeitgleich mit der Strahlung des endgültigen Verdampfens wieder sichtbar (das Bild bzw. das Licht bleibt für die Zeit der Existenz des SL am EH "gefangen")
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomW
Gast
|
| TomW Verfasst am: 15. Feb 2014 10:28 Titel: |
|
|
| Zitat: | | Die Lösung mit Hawkingstrahlung hatte ich dann im Folgenden beschrieben: die Lösung lautet: der Astronaut erreicht den EH (aus Sicht des Außenstehenden) in endlich ferner Zukunft |
Aber wie beeinflusst die Hawking-Strahlung die Tatsache, wann jemand aus Sicht des Außenstehenden in ein Schwarzes Loch stürzt?
Ansonsten würde - jetzt mal aus der Sicht des Astronauten auf dem kollabierenden Stern - während der extrem kurzen Zeit, in der der Beobachter auf den Schwarzschildradius zustürzt, die gesamte Geschichte des Kosmos in rasendem Zeitraffer vor seinen Augen ablaufen - und bis er den EH erreicht hat, sieht er vielleicht, wie dieser sich bereits zerstrahlt oder es gibt einen Big Rip, der das Loch zerreißt...
|
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5044
|
| DrStupid Verfasst am: 15. Feb 2014 14:41 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | Du kannst keine für den Außenstehenden gültige Zeitkoordinate angeben. |
Dann lautet die Anwort auf meine obige Frage aber nicht, es dauert unendlich lange, sondern es lässt sich nicht sinnvoll beantworten.
| TomS hat Folgendes geschrieben: | | Es geht nicht ums Erreichen (das wird mittels Eigenzeit diskutiert, sondern um das Sehen des Erreichens. |
Wenn es nur um das Sehen ginge, dann wäre die Sache sehr einfach. Der Beobachter sieht nie, wie der Astronaut die Singularität erreicht, aber er sieht das Schwarze Loch verdampfen. Das hilft uns aber nicht wirklich weiter, weil es mir nicht um das ging, was der Außenstehende sieht, sondern was der Astronaut erlebt. Die Sicht des Astronauten hilft dabei leider genausowenig, solange wir nicht wissen, wie er die Verdampfung des Loches erlebt. Die Frage ist, ob der schrumpfende EH ihn genauso wieder freigibt, wie er ihn bei der Expansion verschluckt hat.
| TomS hat Folgendes geschrieben: | | DrStupid hat Folgendes geschrieben: | | Wandert es mit dem schrumpfenden Horizont nach innen? |
Ja, sozusagen. Der Horizont ist eine lichtartige Fläche. |
Das heißt doch aber erstmal nur, dass das Licht auf einem stationären Horizont verbleibt, aber nicht notwendigerweise, dass es sich mit einem expandierenden oder schrumpfenden Horizont mitbewegt.
| TomW hat Folgendes geschrieben: | | bis er den EH erreicht hat, sieht er vielleicht, wie dieser sich bereits zerstrahlt oder es gibt einen Big Rip, der das Loch zerreißt... |
Zunächst würde er "sehen", wie der EH sich ausdehnt und ihn verschluckt. Aber dann greift Deine Argumentation. Aus Sicht des Astronauten würde der EH im selben Augenblick wieder schrumpfen und die Frage ist, was dabei mit ihm passiert.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18088
|
| TomS Verfasst am: 15. Feb 2014 16:01 Titel: |
|
|
| TomW hat Folgendes geschrieben: | | Aber wie beeinflusst die Hawking-Strahlung die Tatsache, wann jemand aus Sicht des Außenstehenden in ein Schwarzes Loch stürzt? |
Ohne Hawkingstrahlung existieren das SL und der EH (aus Sicht des Außenstehenden) unendlich lange; mit Hawkingstrahlung existieren das SL und der EH (aus Sicht des Außenstehenden) nur endlich lange.
Ich habe eigtl. alles erklärt, was notwendig ist. Verstehst du nicht, was ich geschrieben habe? Verstehst du das RZ-Diagramm in dem Link? Sind dir Formeln lieber?
| TomW hat Folgendes geschrieben: | | Ansonsten würde während der extrem kurzen Zeit, in der der Beobachter auf den Schwarzschildradius zustürzt, die gesamte Geschichte des Kosmos in rasendem Zeitraffer vor seinen Augen ablaufen |
Nein. Warum spekulierst du jetzt über andere Themen, während die erste Frage noch nicht geklärt ist?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18088
|
| TomS Verfasst am: 15. Feb 2014 16:52 Titel: |
|
|
| DrStupid hat Folgendes geschrieben: | | Dann lautet die Antwort auf meine obige Frage aber nicht, es dauert unendlich lange, sondern es lässt sich nicht sinnvoll beantworten. |
Ich verstehe nicht, was du meinst. Hatte ich das bzgl. des Sturzes ins Zentrum geschrieben? Dann war es entweder unsauber formuliert, oder es handelt sich um ein Missverständnis.
| DrStupid hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Du kannst keine für den Außenstehenden gültige Zeitkoordinate angeben. |
Dann lautet die Antwort auf meine obige Frage aber nicht, es dauert unendlich lange, sondern es lässt sich nicht sinnvoll beantworten. |
Also nochmal:
Die Zeit, die für den Außenstehenden verstreicht, bis der Astronaut den EH erreicht, ist unendlich/endlich lange, wenn du ohne/mit Hawkingstrahlung argumentierst. Dafür ist die Schwarzschild-Zeitkoordinate geeignet.
Wie lange es dauert, bis der Astronaut aus Sicht des Außenstehenden die Singularität erreicht, müsste in anderen Koordinaten formuliert werden. Ich kenne keine, die dafür geeignet wären (weil man nicht mehr von einer globalen Zeit sprechen kann, wenn Terme der Form dx dt auftreten), aber das bedeutet nicht, dass es prinzipiell keine gibt. Was man sagen kann ist, dass es in einer global gültigen Koordinate abc so und so lange dauert. Aber ob abc eine sinnvolle „Zeit“ ist, ist eine andere Frage.
Hoffe, damit ist das klar.
| DrStupid hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Es geht nicht ums Erreichen (das wird mittels Eigenzeit diskutiert, sondern um das Sehen des Erreichens. |
Wenn es nur um das Sehen ginge, dann wäre die Sache sehr einfach. |
Für die Frage von TomW ging es ums „Sehen bis zum EH“.
| DrStupid hat Folgendes geschrieben: | | Der Beobachter sieht nie, wie der Astronaut die Singularität erreicht, aber er sieht das Schwarze Loch verdampfen. |
Ja.
| DrStupid hat Folgendes geschrieben: | | Das hilft uns aber nicht wirklich weiter, weil es mir nicht um das ging, was der Außenstehende sieht, sondern was der Astronaut erlebt. |
Dir nicht, aber TomW schon.
| DrStupid hat Folgendes geschrieben: | | Die Frage ist, ob der schrumpfende EH ihn genauso wieder freigibt, wie er ihn bei der Expansion verschluckt hat. |
Ja, das habe ich schon verstanden, das war deine Frage. Ich habe auch versucht, sie zu beantworten, und ich habe festgestellt, dass ich es ggw. nicht kann:
| TomS hat Folgendes geschrieben: | … mir ist tatsächlich nicht klar, wie man zeigen kann, dass ein innerhalb des EHs gefangener Beobachter die Singularität erreicht, bevor das SL vollständig verdampft. Gründe:
1) ich kenne keine semiklassische Lösung der ART für "dM/dt < 0 plus Strahlung" (die bekannten SL-Lösungen gehen ja von dM/dt = 0 aus)
2) ich kenne erst recht keine semiklassische Lösung für dieses Szenario, die den Innenraum mit einschließt
3) zu lösen wäre die Geodätengleichung des Beobachters d.h. sein x(s), sowie die Lösung für den Horizont d.h. R(t), jeweils in geeigneten Koordinaten; zu zeigen wäre, ob x(s) den Horizont bei R(t) schneidet oder nicht; ohne (2) ist das nicht lösbar
4) ich finde kein Argument, das ohne diese mathematische Betrachtung auskommt |
| TomS hat Folgendes geschrieben: | | … es heißt jedoch noch nicht, dass der Astronaut nach der Überquerung des EH auch die Singularität vor der Zerstrahlung erreicht |
| TomS hat Folgendes geschrieben: | | Die ganze Diskussion leidet natürlich darunter, dass man für die Metrik keine exakte Lösung hat. |
| DrStupid hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | DrStupid hat Folgendes geschrieben: | | Wandert es mit dem schrumpfenden Horizont nach innen? |
Ja, sozusagen. Der Horizont ist eine lichtartige Fläche. |
Das heißt doch aber erstmal nur, dass das Licht auf einem stationären Horizont verbleibt, aber nicht notwendigerweise, dass es sich mit einem expandierenden oder schrumpfenden Horizont mitbewegt. |
Doch, genau das heißt es, und zwar trivialerweise.
Der Horizont ist, unabhängig von seiner „Dynamik“, eine lichtartige Fläche. Er besteht aus der Gesamtheit aller lichtartigen Geodäten, die das Zentrum des SLs nie erreichen (man muss eigtl. mathematisch betrachtet andere Definitionen benutzen, wie isolierte Horizonte o.ä., aber das spielt hier keine Rolle). Jedenfalls ist der Horizont als lichtartige Fläche definiert, und daher bewegen sich die Lichtstrahlen trivialerweise auf dieser lichtartigen Fläche, einfach weil sie so definiert ist.
| DrStupid hat Folgendes geschrieben: | | Aber dann greift Deine Argumentation. |
Das wissen wir nicht (dazu wissen wir noch zu wenig über die RZ-Geometrie im Inneren eines schrumpfenden EHs)
| DrStupid hat Folgendes geschrieben: | | Zunächst würde er "sehen", wie der EH sich ausdehnt und ihn verschluckt. … Aus Sicht des Astronauten würde der EH im selben Augenblick wieder schrumpfen und die Frage ist, was dabei mit ihm passiert. |
Was wir wissen ist, dass wenn der Astronaut genügend rechtzeitig in ein genügend großes SL fällt, er den EH sicher vor dessen Zerstrahlung überquert. Und wir wissen, dass wenn der Astronaut genügend spät in ein genügend kleines SL fällt, aus seiner Sicht das SL und damit der EH vor dem Erreichen des EH verschwindet.
Was wir ohne eine (zumindest semiklassische) Lösung Einsteingleichungen unter Berücksichtigung der Hawkingstrahlung nicht wissen ist, wie genau der EH schrumpft und wie sich das insbs. auf die Geometrie und damit die Geodäte des Astronauten im Innenraum auswirkt.
Die Argumentation im Außenraum beruht bisher auf der Annahme, dass man den schrumpfenden EH sozusagen als zeitlich rückwärts laufenden Film des wachsenden EHs ansehen kann. Das ist aber ziemlich sicher nicht vollständig richtig. Der zeitlich wachsende EH ist eine exakte, die sogenannten Snyder-Oppenheimer-Lösung. Für den schrumpfenden EH kenne ich keine allgemein akzeptierte Lösung. Die Snyder-Oppenheimer-Lösung beschreibt kollabierenden Staub, für den schrumpfenden EH müsste man aber einfallende Materie negativer Energie ansetzen. Das ist sicher etwas ganz anderes.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 15. Feb 2014 19:46, insgesamt einmal bearbeitet |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18088
|
|
|
TomW
Gast
|
| TomW Verfasst am: 15. Feb 2014 20:46 Titel: |
|
|
OK - wenn ich gerade mordsmäßig auf der Leitung stehe, tut's mir leid, ich machs nicht mit Absicht.
Die Aussage
| Zitat: | | Die Lösung ohne Hawkingstrahlung ist klar: der Astronaut erreicht den EH (aus Sicht des Außenstehenden) in unendlich ferner Zukunft, das SL existiert unendlich lange. Die Lösung mit Hawkingstrahlung hatte ich dann im Folgenden beschrieben: die Lösung lautet: der Astronaut erreicht den EH (aus Sicht des Außenstehenden) in endlich ferner Zukunft, sein Bild beim Überqueren des EHs wird zeitgleich mit der Strahlung des endgültigen Verdampfens wieder sichtbar (das Bild bzw. das Licht bleibt für die Zeit der Existenz des SL am EH "gefangen") |
habe ich jetzt so verstanden:
Bedingung A: Keine Hawkingstrahlung
-> Folge 1: Astronaut erreicht EH aus Sicht des weit entfernten Beobachters erst nach unendlich langer Zeit
-> Folge 2: SL existiert unendlich lange, da es nicht zerstrahlt
Bedingung B: Hawkingstrahlung (= Realität):
-> Folge 1: Astronaut erreicht EH auch aus Sicht des weit entfernten Beobachters nach endlicher Zeit
-> Folge 2: Loch verdampft nach endlicher Zeit
Wenn ich das irgendwie falsch verstanden habe, korrigiere mich bitte.
Dass das Loch durch die Hawkingstrahlung nach endlicher Zeit verdampft, ist mir vollkommen klar. Nur Folge 1 verstehe ich nicht: Warum der Astronaut durch die Existenz von Hawkingstrahlung in endlicher Zeit den EH erreicht.
|
|
|
Günther
Anmeldungsdatum: 23.11.2010
Beiträge: 305
|
| Günther Verfasst am: 16. Feb 2014 10:24 Titel: |
|
|
| TomS hat Folgendes geschrieben: |
Die Zeit, die für den Außenstehenden verstreicht, bis der Astronaut den EH erreicht, ist unendlich/endlich lange, wenn du ohne/mit Hawkingstrahlung argumentierst. Dafür ist die Schwarzschild-Zeitkoordinate geeignet.
|
Verläuft denn der Lichtkegel nicht ohne/mit Hawkingstrahlung gleichermaßen am Ereignishorizont tangential? Dann allerdings würde ich erwarten, daß das Kriterium dafür, wann der Astronaut aus der Sicht der entfernten Beobachters den EH erreicht, nicht von der Hawkinstrahlung abhängt, sondern nur davon, ob er ihn in seiner Eigenzeit überquert.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18088
|
| TomS Verfasst am: 16. Feb 2014 11:20 Titel: |
|
|
| TomW hat Folgendes geschrieben: | | Warum der Astronaut durch die Existenz von Hawkingstrahlung in endlicher Zeit [aus Sicht des Außenstehenden] den EH erreicht. |
Der wesentliche Punkt ist, dass der EH bei Berücksichtigung der Hawkingstrahlung nur endlich lange existiert. Damit liegt anschließend wieder eine globale Zeitkoordinate gültig; und damit bleibt auch das Licht nicht unendlich lange "gefangen".
Ich denke, man muss hier wieder sauber zwischen der Zeitkoordinate des externen Beobachters und der Wahrnehmung der Lichtstrahlen durch diesen unterscheiden.
(1) Wenn der EH nach endlicher Zeit verschwindet und man sich das gleichsam als rückwärtslaufenden Film der Entstehung des EH vorstellt, dann sollte wieder eine globale Zeitkoordinate existieren, gemäß der der fallende Astronaut den EH bzw. das zeitliche Ende der Existenz des EH erreicht.
(2) Dass damit sein Bild auch wieder sichtbar wird, setzt zudem voraus, dass in diesem Moment die Lichtkegel nach außen kippen und zugleich mit der letzten Hawkingstrahlung auch die "gefangenen Bilder" freigeben.
(1) ist natürlich eine Annahme, da man die Lösung nicht exakt kennt. Aber ich denke, die Annahme ist vernünftig.
(2) ist eine noch wesentlich weitergehende Annahme. Auch diese ist jedoch sinnvoll, denn wenn man die Sichtbarkeit des letzten Lichtblitzes voraussetzt, dann darf man auch das Sichtbarwerden der "gefangen Bilder" annehmen.
Ich schlage jedoch vor, dass wir diese Spekulationen über das Ende des SLs einstellen, denn wir wissen ziemlich sicher, dass hier die semiklassischen Gleichungen ungültig werden. Wir reden also über mathematische Gleichungen, deren physikalische Relevanz hier sicher nicht mehr gegeben ist.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomW
Gast
|
| TomW Verfasst am: 16. Feb 2014 16:44 Titel: |
|
|
| Zitat: | | Der wesentliche Punkt ist, dass der EH bei Berücksichtigung der Hawkingstrahlung nur endlich lange existiert. Damit liegt anschließend wieder eine globale Zeitkoordinate gültig; und damit bleibt auch das Licht nicht unendlich lange "gefangen". |
Ach so - wenn du also sagst,
| Zitat: | | der Astronaut erreicht den EH (aus Sicht des Außenstehenden) in endlich ferner Zukunft |
dann ist damit gemeint, dass er den EH in dem Moment erreicht, in dem das Schwarze Loch endgültig zerstrahlt (und der EH damit verschwunden ist) - sowohl aus seiner als auch aus der Sicht des Außenstehenden.
Das heißt aber dann im Umkehrschluss, solange das Loch noch nicht zerstrahlt ist, kann der Astronaut den EH nicht erreichen - und somit auch beispielsweise das Loch nicht "füttern". Also sind die Behauptungen vom "alles verschlingenden und dadurch immer weiter anwachsenden" SL Unsinn?
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18088
|
| TomS Verfasst am: 16. Feb 2014 18:29 Titel: |
|
|
| TomW hat Folgendes geschrieben: | … wenn du also sagst,
| Zitat: | | der Astronaut erreicht den EH (aus Sicht des Außenstehenden) in endlich ferner Zukunft |
dann ist damit gemeint, dass er den EH in dem Moment erreicht, in dem das Schwarze Loch endgültig zerstrahlt |
aus Sicht des Außenstehenden sozusagen ja
| TomW hat Folgendes geschrieben: | | … sowohl aus seiner Sicht |
Nein. Warum? Aus seiner Sicht kann er den EH nach relativ kurzer Zeit erreichen, während die Zerstrahlung in sehr ferner Zukunft stattfinden wird.
Die Eigenzeit des Astronauten und die Koordinatenzeit des Außenstehenden haben wenig miteinander zu tun. Insbs. ist die Transformation zwischen beiden singulär am EH, d.h. was für den Außenstehenden in unendlich ferner Zukunft stattfindet, findet für den frei fallenden Astronauten in endlicher Eigenzeit statt.
| TomW hat Folgendes geschrieben: | | Das heißt aber dann im Umkehrschluss, solange das Loch noch nicht zerstrahlt ist, kann der Astronaut den EH nicht erreichen ... |
Aus Sicht des Außenstehenden - ja. Aus seiner Sicht - nein.
| TomW hat Folgendes geschrieben: | | Also sind die Behauptungen vom "alles verschlingenden und dadurch immer weiter anwachsenden" SL Unsinn? |
Nein. Definitiv nicht. Die in das SL fallende Materie überquert in endlicher Eigenzeit den EH, d.h. aus Sicht der Materie stimmt das schon mal. Aus Sicht des Außenstehenden kommt die Materie dem EH innerhalb endlicher Zeit fast beliebig nahe (@DrStupid: wir hatten mal ausgerechnet, dass die Zeitintervalle von ausgesandten Lichtblitzen nur logarithmisch divergieren). Für die Gravitationswirkung eines SLs auf den Außenstehenden ist es übrigens gleichgültig, ob die Materie den EH überschritten hat oder nicht. Die Schwarzschildlösung für rotationssymmetrische, statischen Raumzeiten führt (jetzt nicht in der ART sondern in der Newtonschen Näherung) auf ein Gravitationspotential der Form ~ GM/r; ein Beobachter bei R > r spürt genau dieses Gravitationspotential, wobei M die gesamte Masse bezeichnet, die sich näher am Zentrum befindet als er; und wobei es egal ist, ob diese Masse M den EH vollständig überschritten hat oder nicht. Und nicht zuletzt muss man auch berücksichtigen, dass durch die hineinstürzende Masse das SL, d.h. der EH, wächst. Das bedeutet aber, dass Masse knapp außerhalb des EH auch für den außenstehenden Beobachter bedeutet, dass der EH sich sozusagen nach außen beult, der Masse entgegen.
Ich habe den Eindruck, dass dir das auch ohne Hawkingstrahlung noch nicht so ganz klar ist.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomW
Gast
|
| TomW Verfasst am: 17. Feb 2014 06:25 Titel: |
|
|
| Zitat: | TomW hat Folgendes geschrieben:
… wenn du also sagst,
Zitat:
der Astronaut erreicht den EH (aus Sicht des Außenstehenden) in endlich ferner Zukunft
dann ist damit gemeint, dass er den EH in dem Moment erreicht, in dem das Schwarze Loch endgültig zerstrahlt
aus Sicht des Außenstehenden sozusagen ja |
Ah, ja. Gut.
| Zitat: |
TomW hat Folgendes geschrieben:
… sowohl aus seiner Sicht
Nein. |
Das kann aber schlecht sein, oder?
Wenn die beiden Ereignisse - Astronaut erreicht EH und SL zerstrahlt - aus Sicht des Beobachters zur gleichen Zeit und am gleichen Ort stattfinden (also praktisch ein einziges Ereignis sind), dann muss das ja auch für alle anderen Beobachter der Fall sein, den Astronauten eingeschlossen.
| Zitat: | | Aus seiner Sicht kann er den EH nach relativ kurzer Zeit erreichen, während die Zerstrahlung in sehr ferner Zukunft stattfinden wird. |
Das ist ja kein Widerspruch, im Gegenteil.
Wenn sich der Astronaut dem EH annähert, geht seine Uhr von außen gesehen langsamer und langsamer. Umgekehrt geht aus der Sicht des Astronauten die Uhr des Beobachters immer schneller und schneller.
Ich stelle mir vor, der Beobachter hat ausgerechnet, wann das Loch zerstrahlt und einen Countdown eingestellt. Dieser setzt natürlich bei einer extrem hohen Zahl an, da
| Zitat: | | die Zerstrahlung in sehr ferner Zukunft stattfinden wird. |
Aus Sicht des Astronauten beschleunigt dieser Countdown jedoch immer weiter und weiter, je näher er dem EH kommt, der Zähler rast auf null zu, und in dem Moment, in dem der Countdown auf null springt und das Loch zerstrahlt, erreicht er den verschwindenden EH.
| Zitat: | | Für die Gravitationswirkung eines SLs auf den Außenstehenden ist es übrigens gleichgültig, ob die Materie den EH überschritten hat oder nicht. |
Das hatte ich schon vermutet - die Masse ist nun mal da.
| Zitat: | | der EH sich sozusagen nach außen beult, der Masse entgegen. |
Natürlich wächst der Radius des EH durch hineinfallende Massen, aber er kann sich doch schlecht prophylaktisch ausdehnen - wenn er die Masse, die er für dieses Ausdehnen bräuchte, erst durch eben dieses Ausdehnen bekommen kann.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18088
|
| TomS Verfasst am: 17. Feb 2014 06:58 Titel: |
|
|
| TomW hat Folgendes geschrieben: | | Wenn die beiden Ereignisse - Astronaut erreicht EH und SL zerstrahlt - aus Sicht des Beobachters zur gleichen Zeit und am gleichen Ort stattfinden (also praktisch ein einziges Ereignis sind), dann muss das ja auch für alle anderen Beobachter der Fall sein, den Astronauten eingeschlossen. |
Das ist aber nicht so.
Aus Sicht des Außenstehenden wird das Erreichen des Horizontes mit einer am Horizont singuläreren Zeitkoordinate beschrieben. Und das Zerstrahlen des SLs dürfte in der Raumzeit insgs. ebenfalls zu pathologischen Effekten führen. Nach dem Erreichen des EHs in endlicher Eigenzeit bleibt das Bild des Beobachters am (langsam schrumpfenden) Horizont "gefangen", es wird gemeinsam mit dem letzten Licht der endgültigen Zerstrahlung frei, wenn der Horizont bei r=0 konvergiert und verschwindet.
D.h. die Sicht des Außenstehenden bedient sich einer singulären Zeitkoordinate, die des Astronauten einer regulären. In der singulären ist teilweise keine zeitliche Ordnung mehr existent, in der regulären dagegen schon.
| TomW hat Folgendes geschrieben: | | Zitat: | | der EH sich sozusagen nach außen beult, der Masse entgegen. |
Natürlich wächst der Radius des EH durch hineinfallende Massen, aber er kann sich doch schlecht prophylaktisch ausdehnen - wenn er die Masse, die er für dieses Ausdehnen bräuchte, erst durch eben dieses Ausdehnen bekommen kann. |
Doch, das ist so.
Stell dir vor, dass anstelle des Astronauten eine dünne Kugelschale aus Staub (wie wir sie zu Beginn diskutiert hatten) in das SL der Masse M mit Schwarzschildradius R = R(M) stürzt. Die Kugelschale der Masse dm erreiche einen Radius R+dr. Nun sei dr gerade so bemessen, dass die neue Masse M+dm gerade einen Schwarzschildradius R+dr habe. D.h. die Masse M+dm, d.h. die Masse M des SLs plus die Masse dm der Kugelschale befinde sich innerhalb des neuen Schwarzschildradius R+dr. Man kann ja explizit berechnen, dass R(M+dm) = R+dr ist, d.h. tatsächlich dass der EH (infinitesimal) nach außen wächst, wenn die (infinitesimale) Masse dm ihm bis auf dm nahekommt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18088
|
| TomS Verfasst am: 17. Feb 2014 13:00 Titel: |
|
|
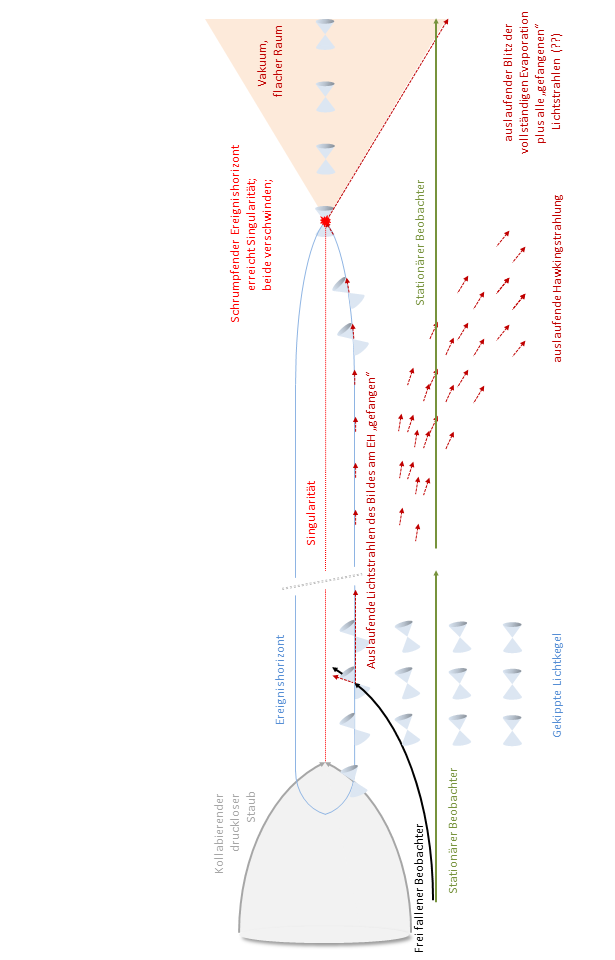
So, ich habe jetzt mal ein eigenes Raumzeitdiagramm erstellt, in dem u.a. die Geschichte des Astronauten darsgestellt ist. Ich habe dabei gezichnet, was aus Hawkings semiklassischer Näherung folgt, deren Ergebnisse wir hier diskutiert hatten. Man beachte jedoch, dass das Ende des SLs sowie die damit verbundene Strahlung sicher nicht mehr im Rahmen der semiklassischen Näherung von Hawking beschrieben werden kann.
Ich hoffe, auf der Basis wird nun einigermaßen klar, wie man sich den Verlauf vorstellen muss.
| Beschreibung: |
| Raumzeitdiagramm des schwarzen Lochs |
|
| Dateigröße: |
52.9 KB |
| Angeschaut: |
4911 mal |
|
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomW
Gast
|
| TomW Verfasst am: 17. Feb 2014 15:10 Titel: |
|
|
| Zitat: | | dass der EH (infinitesimal) nach außen wächst, wenn die (infinitesimale) Masse dm ihm bis auf dm nahekommt. |
Ah, ich glaube, jetzt wird's so langsam.
Das heißt also, dass in dem Moment, an dem sich die hineinstürzende Masse weit genug angenähert hat, um den "gemeinsamen" Schwarzschildradius zu überschreiten, sich praktisch ein neuer Ereignishorizont über sie stülpt.
| Zitat: | | D.h. die Sicht des Außenstehenden bedient sich einer singulären Zeitkoordinate, die des Astronauten einer regulären. In der singulären ist teilweise keine zeitliche Ordnung mehr existent, in der regulären dagegen schon. |
Dann schicke ich den Astronauten mal in den Ruhestand und konzentriere mich wieder ganz auf den Beobachter...
Der Beobachter könnte diesen Moment, an dem der Astronaut verschluckt wird (den gemeinsamen Schwarzschildradius erreicht), also rein theoretisch berechnen. Dann müssten in diesem Moment die sowieso schon stark gedehnten Lichtwellen des Hineinfallenden abrupt abbrechen, oder nicht? Damit wäre aber das "Verschwinden" des Hineinstürzenden von außen weit vor der Zerstrahlung zu sehen (wenn er nicht gerade in letzter Minute reinstürzt).
Die Zeichnung ist nicht schlecht, danke. Ich freue mich natürlich, dass sich jemand so viel Mühe macht!
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18088
|
| TomS Verfasst am: 17. Feb 2014 16:49 Titel: |
|
|
| TomW hat Folgendes geschrieben: | | Das heißt also, dass in dem Moment, an dem sich die hineinstürzende Masse weit genug angenähert hat, um den "gemeinsamen" Schwarzschildradius zu überschreiten, sich praktisch ein neuer Ereignishorizont über sie stülpt. |
sic est
| TomW hat Folgendes geschrieben: | | Der Beobachter könnte diesen Moment, an dem der Astronaut verschluckt wird (den gemeinsamen Schwarzschildradius erreicht), also rein theoretisch berechnen. |
Ja, wenn sich der Beobachter mit der ART auskennt, kann er das berechnen.
| TomW hat Folgendes geschrieben: | | Dann müssten in diesem Moment die sowieso schon stark gedehnten Lichtwellen des Hineinfallenden abrupt abbrechen, oder nicht? |
Was meinst du mit „in diesem Moment“?
| TomW hat Folgendes geschrieben: | | Damit wäre aber das "Verschwinden" des Hineinstürzenden von außen weit vor der Zerstrahlung zu sehen (wenn er nicht gerade in letzter Minute reinstürzt). |
Nein. Das „endgültige Verschwinden“ fällt mit dem Überschreiten des Horizontes zusammen. Bereits vorher wird es ja immer länger dauern, bis die Lichtstrahlen den Beobachter erreichen.
Ich habe nochmal eine andere Zeichnung angefertigt, die eine andere (konforme) Abbildung der Raumzeit in einem sogenannten Penrose-Diagramm zeigt. Die Darstellung hat einige Nachteile; aber der wesentliche Vorteil ist, dass auslaufende (einlaufende) Lichtstrahlen immer und überall einen 45° (-45°) Winkel aufweisen. Man sieht, wieder, dass alle auslaufenden Lichtsignale, die am EH abgestrahlt werden, auf diesem verbleiben. Der EH ist selbst ebenfalls im 45° Winkel gezeichnet, d.h. er entspricht einer lichtartigen Fläche. Was man in dem Bild noch besser erkennt ist, dass die Hawkingstrahlung und das Verdampfen des SLs zu seltsamen Effekten führen, insbs. zu dem doppelten Knick oben, wo jeweils r=0 vermerkt ist. Wie gesagt, in diesem Bereich ist die semiklassische Näherung Hawkings für klassische Raumzeit + freie Quantenfeldtheorie sicher nicht mehr zutreffend.
| Beschreibung: |
|
Download |
| Dateiname: |
Folie2.PNG |
| Dateigröße: |
48.73 KB |
| Heruntergeladen: |
902 mal |
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomW
Gast
|
| TomW Verfasst am: 17. Feb 2014 17:30 Titel: |
|
|
| Zitat: |
TomW hat Folgendes geschrieben:
Dann müssten in diesem Moment die sowieso schon stark gedehnten Lichtwellen des Hineinfallenden abrupt abbrechen, oder nicht?
Was meinst du mit „in diesem Moment“? |
Damit meine ich: Der Beobachter hat zB ausgerechnet, dass die hineinstürzende Masse genau zum Zeitpunkt t den Schwarzschildradius der kombinierten Massen unterschreitet (was ja auch kein Problem ist, da besagte Masse sich schnell beliebig nahe an den alten EH annähert).
Er wartet also diesen Zeitpunkt ab und beobachtet die fallende Masse. Erst erreichen ihn noch stark rotverschobene Lichtwellen, sobald dann die Masse diesen kritischen Radius unterschreitet (diesen Zeitpunkt hat er ja berechnet), wird sie vom neuen EH überstülpt und die Wellen müssten abrupt abbrechen.
Oder meintest du mit | Zitat: | | kann er das berechnen |
dass er den Zeitpunkt aus Sicht des frei Fallenden berechnet?
Die Grafik sieht interessant aus, ich habe aber im Moment keine Zeit, sie genauer anzusehen; ich wollte das hier nur kurz loswerden. Das Diagramm schaue ich mir dann demnächst genauer an.
|
|
|
Günther
Anmeldungsdatum: 23.11.2010
Beiträge: 305
|
| Günther Verfasst am: 17. Feb 2014 18:15 Titel: |
|
|
| TomW hat Folgendes geschrieben: | Das ist ja kein Widerspruch, im Gegenteil.
Wenn sich der Astronaut dem EH annähert, geht seine Uhr von außen gesehen langsamer und langsamer. Umgekehrt geht aus der Sicht des Astronauten die Uhr des Beobachters immer schneller und schneller.
|
Das erste ist richtig, das zweite falsch. Du beschreibst hier die Sicht eines außerhalb des EH stationären Beobachters.
Im Unterschied zu diesem entfernt sich der frei fallenden Astronaut vom entfernten Beobachter (am Horizont mit c), woraus eine Rotverschiebung resultiert. Dazu addiert sich eine gravitative Blauverschiebung, sodaß er
demnach netto eine Rotverschiebung sieht.
Deshalb stimmen auch deine Folgeüberlegungen nicht.
|
|
|
Günther
Anmeldungsdatum: 23.11.2010
Beiträge: 305
|
| Günther Verfasst am: 17. Feb 2014 18:26 Titel: |
|
|
| Günther hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: |
Die Zeit, die für den Außenstehenden verstreicht, bis der Astronaut den EH erreicht, ist unendlich/endlich lange, wenn du ohne/mit Hawkingstrahlung argumentierst. Dafür ist die Schwarzschild-Zeitkoordinate geeignet.
|
Verläuft denn der Lichtkegel nicht ohne/mit Hawkingstrahlung gleichermaßen am Ereignishorizont tangential? Dann allerdings würde ich erwarten, daß das Kriterium dafür, wann der Astronaut aus der Sicht der entfernten Beobachters den EH erreicht, nicht von der Hawkinstrahlung abhängt, sondern nur davon, ob er ihn in seiner Eigenzeit überquert. |
Tom, wie würdest du widerlegen, daß aus der Sicht des Außenstehenden der Astronaut den EH beim Szenario "mit Hawkingstrahlung" ebenfalls in unendlicher Zeit erreicht, sofern dieser den EH in seiner Eigenzeit überquert?
|
|
|
|
|
Registrieren
Login
FAQ
Suchen
