| Autor |
Nachricht |
Xeal
Anmeldungsdatum: 29.05.2007
Beiträge: 243
|
 Xeal Verfasst am: 25. Jun 2007 20:44 Titel: Unwucht einer Scheibe Xeal Verfasst am: 25. Jun 2007 20:44 Titel: Unwucht einer Scheibe |
 |
|
Hallo !
Eine 3 cm dicke, homogene Scheibe mit dem Radius 30 cm und der Masse 5 kg drehe sich mit
w = 10 rad/s um eine Achse, die parallel zu ihrer Achse verläuft und 0, 5 cm von dieser entfernt ist.
(a) Bestimmen Sie die durch diese Unwucht hervorgerufene Kraft auf die Lager.
(b) Wo muss ein Massestück von 100 g auf der Scheibe angebracht werden, um diese Unwucht
auszugleichen?
Wir haben heute in der Gruppe zwei Lösungsansätze zu Aufgabe a besprochen:
1) 
Wobei Mit E_rot jeweils die Rotationsenergien einmal bezüglich der SChwerpunktachse und einmal bezüglich der verschobenen Achse sind.
s: 0,5 cm.
2) Wir haben die Scheibe in zwei Hälften geteilt und als system von zwei Massenpunkten betrachtet. Wobei wir uns für die Gesamtkraft folgendes überlegt haben:

Wobei F_z jweils die Zentripetalkraft ist.
Kann mir jemand ein Feedback zu den beiden Ansätzen geben ?
Gruß
Xeal |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 26. Jun 2007 14:50 Titel: dermarkus Verfasst am: 26. Jun 2007 14:50 Titel: |
 |
|
|
Ich versteh grad nicht so ganz: Wenn ihr diese Ansätze schon besprochen habt, wo ist dann deine Frage? Magst du mal selbst sagen, was du dazu schon verstanden hast, und wo du meinst, dass es bei dir eventuell noch hakt? |
|
 |
Xeal
Anmeldungsdatum: 29.05.2007
Beiträge: 243
|
 Xeal Verfasst am: 26. Jun 2007 16:45 Titel: Xeal Verfasst am: 26. Jun 2007 16:45 Titel: |
 |
|
Tut mir leid, ich vermute meine formulierung war ungeschickt gewählt.
Wir wissen nicht welcher der Ansätze richtig ist und deshalb wollte ich hier mal nachfragen, ob vielleicht jemand sieht, ob die Ansätze richtig oder falsch sind.. |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 27. Jun 2007 14:57 Titel: dermarkus Verfasst am: 27. Jun 2007 14:57 Titel: |
 |
|
Ich finde, auf den ersten Blick sehen die beiden Ansätze schon mal nicht schlecht aus.
Magst du beim ersten Ansatz dazusagen, wie ihr darauf gekommen seid, dass die Kraft F entlang des Weges s konstant sein soll? Was meinst du, wird diese Anahme erfüllt sein, oder magst du lieber erstmal nicht davon ausgehen?
Warum habt ihr beim zweiten Ansatz das Ganze in zwei Teile geteilt, und nicht, zum Beispiel, in 4 oder in 10? Macht das für das Ergebnis der Berechnungen einen Unterschied? Tipp: Was passiert, wenn ihr das ganze in unendlich viele Teile teilt? |
|
 |
Xeal
Anmeldungsdatum: 29.05.2007
Beiträge: 243
|
 Xeal Verfasst am: 27. Jun 2007 15:35 Titel: Xeal Verfasst am: 27. Jun 2007 15:35 Titel: |
 |
|
Hallo !
Wir sind davon ausgegangen, dass die Kraft entlang des Weges Konstant ist, da sich die scheibe ja mit konstanter Winkelgeschwindigkeit bewegt.
Wenn man die Felgen von einem auto auswuchtet, bringt man ja auch nur Gewichte an, die die Kraft auf die Lager dauerhaft kompensiert. Wenn die Kraft nicht konstant wäre, dann müsste man ja während der Fahrt die Auswuchtgewichte abwechselnd anbringen und wieder abmachen..
Zum zweiten Ansatz:
Wir haben die Scheibe in zwei Kreisssegmente geteilt, davon den Schwerpunkt bestimmt und dann das Problem der rotierenden Scheibe in ein Problem der rotierenden Hantel umgewandelt.
Die Zentripetalkräfte der beiden "Hantelmassen" sind entgegengesetzt gerichtet, wobei eine der beiden größer ist. Die resultierende Kraft ist laut unserem Ansatz also die Kraft auf das Lager...
Letztendlich haben wir uns nun für den zweiten Ansatz entschieden, da unserer Meinung nach der Weg im Ansatz 1 gleich 0 ist (die achse wir ja eigentlich gar nicht bewegt).
Problem beim zweiten Ansatz: Als ergebnis bekommen wir eine verschwindent geringe Kraft von ca. 0,033 N (evtl. leichte Rundungsfehler).
in b) haben wir dann so angesetzt, dass die Zentripetalkraft des Auswuchtgewichts genau gleich groß der Kraft auf die Lager sein muss.
Wobei wir dann für den Abstand des Auswuchtgewichts zur Drehachse einen Abstand von 0.456 mm bekommen .....
Das erscheint uns leider wenig realistisch |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 27. Jun 2007 16:05 Titel: dermarkus Verfasst am: 27. Jun 2007 16:05 Titel: |
 |
|
Einverstanden, wenn ihr den Weg im ersten Ansatz als s=0 meint, dann hilft euch dieser Ansatz nichts zum berechnen der Kraft. (Wenn ihr den Weg als den Weg gemeint hättet, den der Mittelpunkt des Rades beim Verschieben von der symmetrischen Position zur Verschobenen Position zurückgelegt hat, dann wäre wiederum die Kraft in Abhängigkeit dieses Weges nicht konstant.)
Für euren zweiten Weg habt ihr durch Ausrechnen ofenbar bereits gemerkt, dass er kein sinnvolles Ergebnis liefert. Habt ihr schon die Vermutung gehabt, dass das daran liegt, dass ihr die Massen der beiden Teile als jeweils im Schwerpunkt des Teiles vereinigt angenommen habt, und dass solche Näherungen bei Drehbewegungen nicht zum Erfolg führen? (Denn bei einem symmetrisch gelagerten Rad kann man ja auch nicht annehmen, dass seine Masse im Schwerpunkt vereinigt sei, das ließe das Tragheitsmoment des Rades ja auf Null schrumpfen.)
Was meinst du zu dem Tipp mit den unendlich vielen Teilen? Erinnert er dich an die Integrale, mit denen man zum Beispiel Trägheitsmomente ausrechnet? |
|
 |
Xeal
Anmeldungsdatum: 29.05.2007
Beiträge: 243
|
 Xeal Verfasst am: 27. Jun 2007 16:31 Titel: Xeal Verfasst am: 27. Jun 2007 16:31 Titel: |
 |
|
an Trägheitsmomente haben wir durchaus gedacht.
Bei diesen Ansätzen kamen wir jedoch auch nur zu widersprüchen mit den Ausgangsbedingungen.
Wir haben beispielsweise über den Drehimpuls angesetzt:
Wir haben zwei Drehimpulse betrachtet:
1) Drehimpuls bzgl. der verschobenen Achse
2) Drehimpuls bzgl. der Achse durch den Schwerpunkt
Wir hätten also dann eine Änderung des Drehimpulses. Die Änderung desDrehimpulses wäre gleich einem Drehoment, was wiederum eine beschleunigung zur Folge hätte. Die Scheibe dreht sich jedoch mit konstanter Geschwindigkeit. Also muss dieser Ansatz auch falsch sein 
Hast du noch einen Tipp ? |
|
 |
cst
Anmeldungsdatum: 16.11.2006
Beiträge: 106
|
 cst Verfasst am: 28. Jun 2007 00:32 Titel: cst Verfasst am: 28. Jun 2007 00:32 Titel: |
 |
|
| dermarkus hat Folgendes geschrieben: |
Was meinst du zu dem Tipp mit den unendlich vielen Teilen? Erinnert er dich an die Integrale, mit denen man zum Beispiel Trägheitsmomente ausrechnet? |
Xeal, das ist doch schonmal ein prima Tipp. Dazu noch einer von mir:
Ein unendlich kleines Massestückchen der Masse 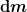 zieht an der Achse mit eine Fliehkraft zieht an der Achse mit eine Fliehkraft

und wegen  und und  kann man kann man  ersetzen. ersetzen. |
|
 |
Xeal
Anmeldungsdatum: 29.05.2007
Beiträge: 243
|
 Xeal Verfasst am: 28. Jun 2007 16:12 Titel: Xeal Verfasst am: 28. Jun 2007 16:12 Titel: |
 |
|
hm ok, das sehe ich ein.
Betrachte ich jetzt als Volumen denn die gesamte Kreissscheibe oder zwei Teile davon ?
Das Volumen kann ich ja leicht ausrechnen, aber wie komme ich dann an dv ?
Muss ich dazu einfach über beide seiten integrieren ? |
|
 |
magneto42
Anmeldungsdatum: 24.06.2007
Beiträge: 854
|
 magneto42 Verfasst am: 28. Jun 2007 22:33 Titel: magneto42 Verfasst am: 28. Jun 2007 22:33 Titel: |
 |
|
|
Ich schlage mal eine alternativen Ansatz vor, der mir einfacher erscheint. Man kann doch das Trägheitsmoment der Rotaionsachse berechnen. Da die Verschiebung von der Mittelachse bekannt ist führt das auf die reduzierte Masse, also die Ersatzmasse, mit gleichem Trägheitsmoment. Dessen Fliehkraft sollte doch die gesuchte Kraft sein. Der zweite Teil der Aufgabe ist dann ein Selbstgänger. |
|
 |
magneto42
Anmeldungsdatum: 24.06.2007
Beiträge: 854
|
 magneto42 Verfasst am: 29. Jun 2007 11:04 Titel: magneto42 Verfasst am: 29. Jun 2007 11:04 Titel: |
 |
|
Sorry, mein Ansatz war wohl nix. Mein Gedankengang über reduzierte Masse und Trägheitsradius führt auf den Holzweg. Besser ist tatsächlich:
 )
Ab zum Integral:

Man schaue hin und erkenne den Schwerpunkt. Damit:

Damit die Unwucht verschwindet muß die Rotationsachse im Schwerpunkt liegen, also:
 |
|
 |
Xeal
Anmeldungsdatum: 29.05.2007
Beiträge: 243
|
 Xeal Verfasst am: 29. Jun 2007 14:51 Titel: Xeal Verfasst am: 29. Jun 2007 14:51 Titel: |
 |
|
so wurde es uns heute auch erklärt  |
|
 |
Fragensteller
Gast
|
 Fragensteller Verfasst am: 24. Aug 2013 03:08 Titel: Erklärung? Fragensteller Verfasst am: 24. Aug 2013 03:08 Titel: Erklärung? |
 |
|
|
Hallo, ist ja sehr lange her. Aber kann mir irgendwer die Lösung erklären? |
|
 |
Systemdynamiker
Anmeldungsdatum: 22.10.2008
Beiträge: 594
Wohnort: Flurlingen
|
 Systemdynamiker Verfasst am: 24. Aug 2013 10:26 Titel: zwei Arten von Unwucht Systemdynamiker Verfasst am: 24. Aug 2013 10:26 Titel: zwei Arten von Unwucht |
 |
|
Man unterscheidet zwei Arten von Unwucht, die statische und die dynamische. Bei der statischen Unwucht liegt der Massenmittelpunkt nicht auf der Drehachse, bei der dynamischen ist die Drehachse nicht Hauptachse des starren Köpres. Im ersten Fall ändert sich der Impulsinhalt und im zweiten Fall der Drehimpulsinhalt des rotierenden Körpers.
Hier handelt es sich um eine statische Unwucht, weil der Massenmittelpunkt nicht auf der Drehachse liegt. Folglich ist die Lagerkraft gleich der Änderungsrate des Impulses. Also Lagerkraft gleich Masse der Scheibe mal Beschleunigung des Massenmittelpunkts der Scheibe. Die Berechnung der Beschleunigung sollte bekannt sein (Kreisbewegung). Beim Auswuchten verschiebt man den Massenmittelpunkt auf die Drehachse.
Siehe auch: https://www.youtube.com/watch?v=LdexQo-xmOg
_________________
Herzliche Grüsse Werner Maurer |
|
 |
Fragensteller
Gast
|
 Fragensteller Verfasst am: 08. Sep 2013 10:15 Titel: Fragensteller Verfasst am: 08. Sep 2013 10:15 Titel: |
 |
|
|
Besten Dank! Insbesondere den Link. |
|
 |
|

















