| Autor |
Nachricht |
ak!!53
Anmeldungsdatum: 12.01.2024
Beiträge: 51
|
 ak!!53 Verfasst am: 05. März 2024 16:09 Titel: Elastischer oder inelastischer Stoß ak!!53 Verfasst am: 05. März 2024 16:09 Titel: Elastischer oder inelastischer Stoß |
 |
|
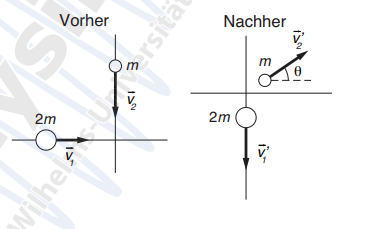
Zwei Bälle mit den Massen m und 2m bewegen sich aus senkrechten Richtungen mit den
Geschwindigkeiten |⃗v1| = v und |⃗v2| = 4v aufeinander zu und kollidieren . Nach
dem Stoß bewegt sich der schwerere Ball nach unten, orthogonal zu seiner ursprünglichen Bewegungsrichtung, mit der Geschwindigkeit |⃗v ′
1| = v. Der leichtere Ball bewegt sich mit einer
Geschwindigkeit ⃗v ′
2 unter einem Winkel θ zur Horizontalen. In dem System gibt es keine Gravitation.
a)Welche Größen sind bei einem
elastischen und einem inelastischen Stoß erhalten?
b) Berechnen Sie den Winkel θ und
den Betrag der Geschwindigkeit |⃗v ′
2|.
c) Stellen Sie die Energiebilanz vor
und nach dem Stoß auf und entscheiden Sie,
ob der Stoß elastisch oder inelastisch ist.
Zu a) habe ich folgendes Geschrieben:
1.Bei einem elastischen Stoß wird die Impulserhaltung berücksichtigt wie auch die E_kin Erhaltung. Daraus folgte 2 Gleichungen, diese vermag ich hier nicht abtippen.
2. Bei einem inelastischen Stoß wird die Impulserhaltungs berücksichtigt aber die E_kin Erhaltung nicht, die kin. Energie wird in verschiedene Formen der Energie umgewandelt wie Wärme und Verformung.
Frage : Ich fand in einem Video im Thumbnail folgende Beziehung noch beim inelastischen Stoß:  Ich bin mir nicht ganz sicher ob diese Beziehung wirklich gilt sag ich mal also lasse ich diese außen vor. Ich bin mir nicht ganz sicher ob diese Beziehung wirklich gilt sag ich mal also lasse ich diese außen vor.
Zu b) Meine Idee und Vorgrehen waren wie folgt:
Aus dem, dass es nicht klar ist, welche Art von Stoß man hat kann man nichts über die E_kin Erhaltung Aussagen.
Aber in beiden Arten von Stößen ist allerdings die Impulserhaltung zu beachten. Da ich 2 Variabeln auszurechnen habe, ist es durchaus klar, dass der Impuls vektoriell zerbrochen werden sollte.
v_2')
v_2')
So, dann habe ich versucht dort eine Beziehung zu finden nach der aufgelöst werden konnte, grade beim Tippen meine ich noch eine gefunden zu haben aber ich mag die nicht jetzt nachprüfen.
Ich habe einen Wert für v_2' erhalten und war so naja zufrieden.
-\sin(\theta)} )
So ich kann mich nun noch an eine andere Stoßaufgabe errinern, wo ich die erhaltene Beziehung in den Anfangsimpuls einsetzte und dann die eigentliche gesuchte Variable bestimmen konnte.
Würde ich hier so vorgehen, würden sich in jeglicher Beziehung die gesuchte Variable erübrigen und damit auch nicht mehr bestimmbar sein. Ist dies also die Lösung ?
Alternativ ist, ich löse nach einer anderen Variable auf, zb. v und setze v dann in den Impulswieder ein und bestimme so mein v_2' .
Ich frage mich dann nur, ob ich dann noch bei der Aufgabe bleibe und nicht einfach versuche rumzurechnen, hoffentlich ist Nachvollziehbar was ich damit ausdrücken möchte.
Zum bestimmen von Theta selbst würde ich eig von der Idee nicht großartig abweichen, ich finde nur, dass es keinen Sinn macht, fragt nich warum, es ist wie ein mulmiges Bauchgefühl.
| Beschreibung: |
|
| Dateigröße: |
23.6 KB |
| Angeschaut: |
4015 mal |
|
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 05. März 2024 17:15 Titel: Re: Elastister oder inelastischer Stoß Myon Verfasst am: 05. März 2024 17:15 Titel: Re: Elastister oder inelastischer Stoß |
 |
|
a): Richtig.
| ak!!53 hat Folgendes geschrieben: | Ich fand in einem Video im Thumbnail folgende Beziehung noch beim inelastischen Stoß:  Ich bin mir nicht ganz sicher ob diese Beziehung wirklich gilt sag ich mal also lasse ich diese außen vor. Ich bin mir nicht ganz sicher ob diese Beziehung wirklich gilt sag ich mal also lasse ich diese außen vor. |
Bei einem vollkommen inelastischen Stoss, wo der grösstmögliche Anteil an kinetischer Energie in andere Energieformen umgewandet wird, bleiben die beiden Stosspartner nach dem Stoss aneinander haften. Das war wohl mit v1'=v2' gemeint.
Zu b): Hier muss der Betrag v2' und der Winkel theta explizit berechnet werden (v2' in Einheiten von v). Wenn Du die Gleichungen für die Impulserhaltung aufstellst mit den unbekannten Komponenten v2x', v2y', kannst Du problemlos nach diesen auflösen. Daraus folgt der Betrag und aus dem Verhältnis v2y'/v2x' der Winkel theta.
|
|
 |
ak!!53
Anmeldungsdatum: 12.01.2024
Beiträge: 51
|
 ak!!53 Verfasst am: 05. März 2024 21:14 Titel: Re: Elastister oder inelastischer Stoß ak!!53 Verfasst am: 05. März 2024 21:14 Titel: Re: Elastister oder inelastischer Stoß |
 |
|
| Myon hat Folgendes geschrieben: | a): Richtig.
| ak!!53 hat Folgendes geschrieben: | Ich fand in einem Video im Thumbnail folgende Beziehung noch beim inelastischen Stoß:  Ich bin mir nicht ganz sicher ob diese Beziehung wirklich gilt sag ich mal also lasse ich diese außen vor. Ich bin mir nicht ganz sicher ob diese Beziehung wirklich gilt sag ich mal also lasse ich diese außen vor. |
Bei einem vollkommen inelastischen Stoss, wo der grösstmögliche Anteil an kinetischer Energie in andere Energieformen umgewandet wird, bleiben die beiden Stosspartner nach dem Stoss aneinander haften. Das war wohl mit v1'=v2' gemeint.
Zu b): Hier muss der Betrag v2' und der Winkel theta explizit berechnet werden (v2' in Einheiten von v). Wenn Du die Gleichungen für die Impulserhaltung aufstellst mit den unbekannten Komponenten v2x', v2y', kannst Du problemlos nach diesen auflösen. Daraus folgt der Betrag und aus dem Verhältnis v2y'/v2x' der Winkel theta. |
Hallo Myon, danke dir, wiedermal, für deine Antwort.
Verstehe ich das richtig, also auch aus deinem Kommentar, dass in der vektoriellen Zerlegung von den beiden Kugeln nach dem Stoß es vollkommen ausreicht in den beiden einzelnen Gleichungen nach der gesuchten Variable aufzulösen ?
Ich denke mir grade folgendes, auch mit dem Begriff des Betrages im Hinterkopf, dass der Betrag die Wurzel aus den beiden Komponenten zum Quadrat ist.
Ah, ich denke ich sehe wie ich zur Lösung komme, undzwar forme ich einfach nach den Unbekannten Variablen um und erhalte somit meine X und Y Komponente um diese im Betrag auszurechnen oder halt darzustellen.
Ich gucke mal wie und was ich dannach für den Winkel erhalten werde, ich wette da gibts dann eine Tangens Beziehung.
Ich edite und melde mich.
|
|
 |
ak!!53
Anmeldungsdatum: 12.01.2024
Beiträge: 51
|
 ak!!53 Verfasst am: 06. März 2024 11:49 Titel: ak!!53 Verfasst am: 06. März 2024 11:49 Titel: |
 |
|
Für die einzelnen Komponenten der Geschwindigkeiten habe ich folgendes raus.


Diese beiden lassen sich als Quadrat erstmal so nicht addieren, da muss man den Bruch erweitern unterhalb der Wurzel. Dann ist durch ein Additionstheorem nur die Geschwindigkeit noch im Zähler aber im Nenner kriege ich nach dem Wurzel ziehen folgendes:

So, beim Winkel dachte ich mir folgendes, da ich quasi die X und Y Komponente von der Geschwindigkeit nach dem Stoß habe, setze ich die einfach in den Tangens ein, weil der sich eben dafür eignet.
Irgendwie sieht das alles ganz holprig aus und ich finde mit dem vorherig bestimmten Komponenten lässt sich wenig arbeiten.
) nach einsetzen, dachte ich mir, dass es Schwachsinn ist, weil ich kann schwer den Winkel einer Funktion ausrechnen mit dem Winkel selbst in einer anderen Funktion eingebettet. Etwas ist mir noch nicht bewusst oder gar bekannt. Ich finde den Nenner des Betrags auch fragwürdig, denn eine Textstelle von Myon verrät mir, dass der Betrag nur von der Geschwindigkeit abhängen kann. nach einsetzen, dachte ich mir, dass es Schwachsinn ist, weil ich kann schwer den Winkel einer Funktion ausrechnen mit dem Winkel selbst in einer anderen Funktion eingebettet. Etwas ist mir noch nicht bewusst oder gar bekannt. Ich finde den Nenner des Betrags auch fragwürdig, denn eine Textstelle von Myon verrät mir, dass der Betrag nur von der Geschwindigkeit abhängen kann.
Sind damit auch unteranderem meine X und Y Komponenten nicht korrekt ?
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 06. März 2024 15:58 Titel: Myon Verfasst am: 06. März 2024 15:58 Titel: |
 |
|
Für die Impulskomponenten in x-Richtung gilt z.B.

Die Gleichung für den Winkel ist dann richtig.
In c) prüfen, ob mit der berechneten Geschwindigkeit v2' die kinetische Energie erhalten ist.
|
|
 |
ak!!53
Anmeldungsdatum: 12.01.2024
Beiträge: 51
|
 ak!!53 Verfasst am: 06. März 2024 17:00 Titel: ak!!53 Verfasst am: 06. März 2024 17:00 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | Für die Impulskomponenten in x-Richtung gilt z.B.

Die Gleichung für den Winkel ist dann richtig.
In c) prüfen, ob mit der berechneten Geschwindigkeit v2' die kinetische Energie erhalten ist. |
Ah okay, also ist es gar nicht Notwendig mit Winkelbeziehungen den eigentlichen Geschwindigkeitsvektor zu zerteilen. Ich schau mal was ich da rauskriege, eig dürften nur die sin und cos Terme wegfallen. Sowas blödes aber auch, einmal musste ich schon den Impuls vektoriell zerlegen aber dort waren die Winkel auch dann gegeben. Mit denen hatte man dann später Verhältnisse bestimmt usw.
|
|
 |
|
|
















