| Autor |
Nachricht |
ak!!53
Anmeldungsdatum: 12.01.2024
Beiträge: 51
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5875
|
 Myon Verfasst am: 23. Feb 2024 17:43 Titel: Myon Verfasst am: 23. Feb 2024 17:43 Titel: |
 |
|
Nur ein paar Bemerkungen:
Neben Impuls und kin. Energie ist noch eine weitere Grösse erhalten. Da nach dem Stoss 3 Grössen unbekannt sind, ist auch noch eine dritte Gleichung notwendig, damit alle Grössen bestimmt sind.
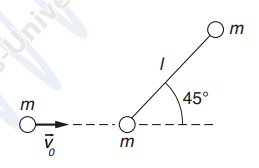
Der Impuls ist noch nicht richtig. In y-Richtung gibt es keine Impulse, wenn sich die Masse m vor dem Stoss parallel zur x-Achse bewegt. Zur kinetischen Energie kommt ein weiterer Term hinzu (an Drehung denken).
Für das Trägheitsmoment musst Du nicht integrieren, Du kannst einfach das Massenträgheitsmoment für einen starren Körper aus Massenpunkten nehmen, siehe hier.
|
|
 |
ak!!53
Anmeldungsdatum: 12.01.2024
Beiträge: 51
|
 ak!!53 Verfasst am: 24. Feb 2024 11:41 Titel: ak!!53 Verfasst am: 24. Feb 2024 11:41 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | Nur ein paar Bemerkungen:
Neben Impuls und kin. Energie ist noch eine weitere Grösse erhalten. Da nach dem Stoss 3 Grössen unbekannt sind, ist auch noch eine dritte Gleichung notwendig, damit alle Grössen bestimmt sind.
Der Impuls ist noch nicht richtig. In y-Richtung gibt es keine Impulse, wenn sich die Masse m vor dem Stoss parallel zur x-Achse bewegt. Zur kinetischen Energie kommt ein weiterer Term hinzu (an Drehung denken).
Für das Trägheitsmoment musst Du nicht integrieren, Du kannst einfach das Massenträgheitsmoment für einen starren Körper aus Massenpunkten nehmen, siehe hier. |
Hi, danke dir für deine Antwort, ich las die gestern Abend abseits meines Schreibtisches. Mir ist folgendes noch eingefallen, dass in der Ekin Gleichung noch die Rotationsenergie vorhanden ist.

Zuvor dachte ich allerdings, dass die 3te fehlende Gleichung eben durch das gleichsetzen der kin. Energie vor dem Stoß = nur der rot. Energie sei. Aber dies würde vorraussetzen, dass zb sich der Stab nicht irgendwie im Raum linear bewegt sonder halt nur um eine feste Achse dreht. Das würde auch meine E_k Erhaltung anders aussehen lassen. Es sei denn ich ersetze die Geschwindigkeiten nach dem Stoß durch eine Winkelgeschwindigkeit. So, dass lässt mich aber immer noch nicht ganz die Aufgabe lösen so ist meine Befürchtung. EDIT" dies geht auch gegen den Aufgabenteil c)"
Beim einsetzen der Rotationsenergie in die kin. E. bleibt mir, momentan, die dritte Gleichung noch unbekannt. Ich versuch mal etwas im Tipler nachzusehen oder im Nolting.
|
|
 |
novae
Gast
|
 novae Verfasst am: 24. Feb 2024 13:50 Titel: novae Verfasst am: 24. Feb 2024 13:50 Titel: |
 |
|
| ak!!53 hat Folgendes geschrieben: |

}{1-2m^2+4m})
|
Die Einheit von v ist m/s. Das kann man hier nicht erkennen
Bei der Drehimpulserhaltung nimmt man als Drehpunkt die Hantelmittelpunkt
dh
 = )
|
|
 |
ak!!53
Anmeldungsdatum: 12.01.2024
Beiträge: 51
|
 ak!!53 Verfasst am: 24. Feb 2024 14:30 Titel: ak!!53 Verfasst am: 24. Feb 2024 14:30 Titel: |
 |
|
| novae hat Folgendes geschrieben: | | ak!!53 hat Folgendes geschrieben: |

}{1-2m^2+4m})
|
Die Einheit von v ist m/s. Das kann man hier nicht erkennen
Bei der Drehimpulserhaltung nimmt man als Drehpunkt die Hantelmittelpunkt
dh
 = ) |
Drehimpulserhaltung ?
Ich muss da einmal den Begriff recherchieren, bezüglich der Geschwindigkeiten die kommen aus den Erhaltungssätze, da mir dort zb die rot. Energie fehlt und eine 3 Gleichung sind diese Ergebnise nicht zu beachten, da einiges an Informationen fehlen zum lösen von c).
Wie ich sehe schreibst, du dass der Drehimpuls am Drehpunkt erhalten bleibt mit halbierung der Gesamtlänge l. Ich werde mich erst morgen leider mit dieser Aufgabe beschäftigen können, daher erwartet nicht ein Antwort vor dem nächsten Tag.
|
|
 |
novae
Gast
|
 novae Verfasst am: 24. Feb 2024 14:48 Titel: novae Verfasst am: 24. Feb 2024 14:48 Titel: |
 |
|
| ak!!53 hat Folgendes geschrieben: |
Wie ich sehe schreibst, du dass der Drehimpuls am Drehpunkt erhalten bleibt |
Jeden beliebigen Punkt kann man als Drehpunkt nehmen. Aber der Hantelmittelpunkt ist am einfachsten. Außerdem soll man omega laut Aufgabenstellung auf den Hantelmittenpunkt (Schwerpunkt) beziehen.
|
|
 |
ak!!53
Anmeldungsdatum: 12.01.2024
Beiträge: 51
|
 ak!!53 Verfasst am: 25. Feb 2024 13:38 Titel: ak!!53 Verfasst am: 25. Feb 2024 13:38 Titel: |
 |
|
So, nach etwas recherche und den Antworten hier. Bin ich zu folgenden Ideen gekommen.
a) Impuls wird erhalten, Ekin wird erhalten (+ Erot) und der Drehimpuls wird erhalten.
Da sich die Hanteln vorher nicht bewegen/drehen ist beim Impuls die Geschwindigkeit der Hantel =0, die kin. Energie = 0 und der Drehimpuls vor der dem Stoß =0.
Das heisst im Umkehrschluss folgendes.
1. 
2. 
3. 
So nun denke ich mir, dass es noch nicht ganz vollständig ist, ich stelle mir folgendes vor, dass die Drehimpulse sich hier zu 0 aufaddieren lassen. Im Umkehrschluss heisst es, dass zb das eine Ende der Hantel einen positiven Drehimpuls hat und die andere Seite einen negativen Drehimpuls.
Selbst wenn ich die einzelnen Drehimpulse versuche zu bestimmen, laufe ich darauf hinaus am Ende zu sagen, dass der eine Drehimpuls gleich dem anderen ist..
Ich finde das hilft mir nicht sonderlich weiter, beachte ich noch etwas nicht ? Oder stelle ich mir dies zu kompliziert vor ?
Zu b)

mit Roh = M/L=dm/dx erhalte ich für das Trägheitsmoment 
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5875
|
 Myon Verfasst am: 25. Feb 2024 14:09 Titel: Myon Verfasst am: 25. Feb 2024 14:09 Titel: |
 |
|
Die Gleichungen für die Impuls- und Energieerhaltung sind richtig.
Weiter ist richtig, dass der Drehimpuls erhalten bleibt. Es kommt nun darauf an, wie man das Koordinatensystem festlegt. Legt man es so fest, dass die einlaufende, freie Kugel sich entlang der x-Achse bewegt, so hat diese Kugel vor und nach dem Stoss keinen Drehimpuls (immer bezogen auf den Ursprung des Koordinatensystems). Der Gesamtdrehimpuls vor dem Stoss ist also gleich null. Der Drehimpuls der Hantel nach dem Stoss kann man in diesem Fall als Summe des Drehimpulses des Schwerpunkts plus des Drehimpulses der Drehung um den Schwerpunkt schreiben. Die Gleichung für die Drehimpulserhaltung wird dann

Eine andere Möglichkeit ist, den Ursprung des Koordinatensystems in den Schwerpunkt der Hantel vor dem Stoss zu legen, wobei sich die einlaufende Kugel parallel zur x-Achse bewegt. Dann wird die Gleichung für den Drehimpuls

Dabei bezeichnet b jeweils den "Stossparameter", d.h. den Abstand der Bahnkurve der freien Kugel vom Schwerpunkt der Hantel, also

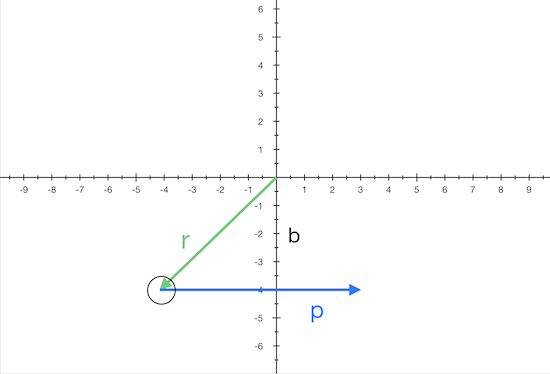
Es mag etwas seltsam erscheinen, dass die freie Kugel einen Drehimpuls hat. Das ist aber der Fall, wenn man sich die Definition
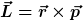
anschaut.
Zum Massenträgheitsmoment: Dein Ergebnis ist noch nicht ganz richtig. Für einen starren Körper bestehend aus Punktmassen gilt

Dabei bezeichnet r_i den senkrechten Abstand der Masse i zur Drehachse, in diesem Fall den Abstand zum Schwerpunkt der Hantel.
|
|
 |
ak!!53
Anmeldungsdatum: 12.01.2024
Beiträge: 51
|
 ak!!53 Verfasst am: 27. Feb 2024 13:30 Titel: ak!!53 Verfasst am: 27. Feb 2024 13:30 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | Die Gleichungen für die Impuls- und Energieerhaltung sind richtig.
Weiter ist richtig, dass der Drehimpuls erhalten bleibt. Es kommt nun darauf an, wie man das Koordinatensystem festlegt. Legt man es so fest, dass die einlaufende, freie Kugel sich entlang der x-Achse bewegt, so hat diese Kugel vor und nach dem Stoss keinen Drehimpuls (immer bezogen auf den Ursprung des Koordinatensystems). Der Gesamtdrehimpuls vor dem Stoss ist also gleich null. Der Drehimpuls der Hantel nach dem Stoss kann man in diesem Fall als Summe des Drehimpulses des Schwerpunkts plus des Drehimpulses der Drehung um den Schwerpunkt schreiben. Die Gleichung für die Drehimpulserhaltung wird dann

Eine andere Möglichkeit ist, den Ursprung des Koordinatensystems in den Schwerpunkt der Hantel vor dem Stoss zu legen, wobei sich die einlaufende Kugel parallel zur x-Achse bewegt. Dann wird die Gleichung für den Drehimpuls

Dabei bezeichnet b jeweils den "Stossparameter", d.h. den Abstand der Bahnkurve der freien Kugel vom Schwerpunkt der Hantel, also

Es mag etwas seltsam erscheinen, dass die freie Kugel einen Drehimpuls hat. Das ist aber der Fall, wenn man sich die Definition
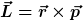
anschaut.
Zum Massenträgheitsmoment: Dein Ergebnis ist noch nicht ganz richtig. Für einen starren Körper bestehend aus Punktmassen gilt

Dabei bezeichnet r_i den senkrechten Abstand der Masse i zur Drehachse, in diesem Fall den Abstand zum Schwerpunkt der Hantel. |
Entschuldige, ich bin seit der Antwort von dir nicht wahrlich in der Aufgabe weitergekommen. Ich weiß selbst nicht ganz wo meine Schwierigkeit liegt deine Angaben zu verstehen.
Ich hab derweilen an anderen gesessen..
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5875
|
|
 |
Isaac Newton
Gast
|
 Isaac Newton Verfasst am: 28. Feb 2024 21:53 Titel: Isaac Newton Verfasst am: 28. Feb 2024 21:53 Titel: |
 |
|
Hallo zusammen
Ich habe eine Frage.
Hätte Newton diese Aufgabe lösen können?
Denn Newton kannte soweit ich weiß die Energieerhaltung nicht.
Diese ist aber anscheinend notwendig um die Aufgabe zu lösen.
MfG
|
|
 |
|
|