| Autor |
Nachricht |
vmax
Gast
|
 vmax Verfasst am: 08. Dez 2015 13:07 Titel: Kollision Relativgeschwindigkeiten vmax Verfasst am: 08. Dez 2015 13:07 Titel: Kollision Relativgeschwindigkeiten |
 |
|
Meine Frage:
Nehmen wir mal an, zwei identische Autos fahren mit 50km/h aufeinander zu. Die Annäherungsgeschwindigkeit beträgt 100km/h. Jedes Auto hat die kinetische Energie E=0.5 x m x v^2. Bei einer Kollision wird die Energie 2E frei.
Nehmen wir einen anderen Fall an: eins der Autos steht, das andere fährt mit 100km/h. Beide Autos nähern sich also wieder mit 100km/h an. Das stehende Auto hätte dann keine kinetische Energie, das fahrende Auto hätte dann durch die doppelte Geschwindigkeit aber die Energie 4E! Das heißt bei einer Kollision würde die doppelte Energie frei!
Das könnten auch Raumschiffe im All sein, wo man nicht festlegen kann wer sich bewegt und wer stillsteht ... das kann doch nicht sein, dass die kinetische Energie von der Betrachtungsweise abhängt, wer steht und wer sich bewegt?
Meine Ideen:
- |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 08. Dez 2015 14:03 Titel: TomS Verfasst am: 08. Dez 2015 14:03 Titel: |
 |
|
Doch, das ist so.
Betrachten wir zwei Geschwindigkeiten und zwei Energien mit i = 1,2 aus Sicht eines Bezugsystems S


Nun transformieren wir in das Ruhesystem S' des zweiten Objektes i = 2
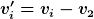


^2)


Das bedeutet, dass die Energie (genauso wie Geschwindigkeit und Impuls) keine skalare Größen sind.
Das ist auch der Grund, warum in der Hochenergiephysik eine andere invariante Größe genutzt wird, um den Prozess zu charakterisieren. Man geht aus von den Viererimpulsen aller beteiligten Objekte (ich setze c = 1)
)
sowie deren Summe
)
Die relevante Größe lautet dann

Sie ist ein Lorentz-Skalar, d.h. invariant unter Lorentz-Transformationen (nicht: Galilei-Transformationen), und sie hat demnach in allen Bezugsystemen den selben Wert
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
MichaelK
Gast
|
 MichaelK Verfasst am: 10. Dez 2015 16:15 Titel: Elastischer/unelastischer Stoß MichaelK Verfasst am: 10. Dez 2015 16:15 Titel: Elastischer/unelastischer Stoß |
 |
|
Sorry, aber TomS Antwort befriedigt mich nicht.
Die Energie ist selbstverständlich eine skalare Größe, schon allein weil die Masse skalar ist und das (Skalar-)Produkt zweier Vektoren (also v**2), wie der Name schon sagt, auch skalar ist.
Was vmax bei seiner Rechnung übersieht, ist die Gesamt-Energie nach dem Stoß. Nehmen wir einfache Zahlen und einen vollkommen unelastischen Stoß: m1=m2=1kg.
1.Fall: v1 = -v2 = 1m/s (Beobachter ruht relativ zum Kollisionspunkt)
E1 = 1/2 * m1 * v1**2 => E1 = 0.5J
E2 = 1/2 * m2 * v2**2 => E2 = 0.5J
Gesamte in Deformation (unelastischer Stoß!) umgesetzte Energie: E1+E2 = 1J
2.Fall: v1 = 0; v2 = 2m/s (Beobachter ruht relativ zu m1)
E1 = 1/2 * m1 * v1**2 => E1 = 0J
E2 = 1/2 * m2 * v2**2 => E2 = 2J
Nach dem Stoß bewegt sich das Gesamtsystem relativ zum Beobachter mit einer Geschwindigkeit ve von -1m/s (aus Gründen der Impulserhaltung). Die Bewegungsenergie Ee dieses Ensembles ist also:
Ee = 1/2 * (m1+m2) * ve**2 = 1J
Damit ist die in Deformation umgesetzte Energie wieder genau 1J. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 10. Dez 2015 21:14 Titel: Re: Elastischer/unelastischer Stoß TomS Verfasst am: 10. Dez 2015 21:14 Titel: Re: Elastischer/unelastischer Stoß |
 |
|
| MichaelK hat Folgendes geschrieben: | Sorry, aber TomS Antwort befriedigt mich nicht.
Die Energie ist selbstverständlich eine skalare Größe, schon allein weil die Masse skalar ist und das (Skalar-)Produkt zweier Vektoren (also v**2), wie der Name schon sagt, auch skalar ist. |
Falsch.
Was ist die Definition einer skalaren Größe? Dass sie in allen Bezugsystemen denselben Wert hat.
| MichaelK hat Folgendes geschrieben: | | Was vmax bei seiner Rechnung übersieht, ist die Gesamt-Energie nach dem Stoß. |
Das ist doch für die Beurteilung, ob eine Größe ein Skalar ist, irrelevant.
Die Energie E bzw. E' ist in beiden Bezugsystemen S bzw. S' erhalten. Aber sie hat in beiden Bezugsystemen jeweils einen anderen Wert.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 11. Dez 2015 07:13, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 10. Dez 2015 22:05 Titel: TomS Verfasst am: 10. Dez 2015 22:05 Titel: |
 |
|
Mir ist dein Missverständnis klar geworden. Du meinst, v^2 wäre eine skalare Größe, weil sie im Gegensatz zum Geschwindigkeitsvektor nicht aus mehreren Komponenten besteht. Das ist leider dir gebräuchliche, jedoch nicht die präzise Definition.
| Wikipedia hat Folgendes geschrieben: | In der Physik werden Skalare verwendet zur Beschreibung physikalischer Größen, die richtungsunabhängig sind. Beispiele für skalare physikalische Größen sind die Masse eines Körpers, seine Temperatur, seine Energie ... Anders gesagt: Eine skalare physikalische Größe ändert sich bei Drehungen nicht ... Aber der Betrag der Geschwindigkeit ändert sich bei Drehungen nicht und ist ein Skalar.
Ob eine Größe ein Skalar ist, hängt von der betrachteten Transformationsgruppe ab. So ist die Energie ein Skalar bezüglich Drehungen, aber in der Relativitätstheorie Komponente eines Vierervektors. |
Das halte ich für ziemlich grausig. Allein der letzte Absatz geht einigermaßen in die richtige Richtung.
In der Newtonschen Mechanik ist die Gruppe der Galilei-Transformationen (geradlinig-gleichförmige Bewegungen, Translationen, Rotationenen in Raum und Zeit) die entscheidende Symmetriegruppe.
Zurück zu Wikipedia: Ob eine Größe ein Skalar ist, hängt von der betrachteten Transformationsgruppe ab - soweit richtig. So ist die Energie in der Newtonschen Mechanik kein Skalar, da sie bzgl. Transformationen der Geschwindigkeit (Boosts) ihren Wert ändert.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
MichaelK
Gast
|
 MichaelK Verfasst am: 11. Dez 2015 10:06 Titel: Elastischer/unelastischer Stoß MichaelK Verfasst am: 11. Dez 2015 10:06 Titel: Elastischer/unelastischer Stoß |
 |
|
Ich denke es gibt hier ein paar Probleme mit den Begrifflichkeiten. M.E. geht es um klassische Newtonsche Mechanik. Der Begriff „Skalar“ im Unterschied zu einem „Vektor“ bedeutet nach Wikipedia „…eine mathematische Größe, die allein durch die Angabe eines Zahlenwertes charakterisiert ist (in der Physik gegebenenfalls mit Einheit).“ In diesem Sinne ist die Energie, anders als beispielsweise die Geschwindigkeit oder der Impuls, ein Skalar. Die mechanische Energie eines bewegten Körpers, in diesem Falle des Autos, hat keine Richtung. Daran ändert auch die Tatsache nichts, daß die Energie in der Relativitätstheorie die Komponente eines Vektors ist. Komponenten eines Vektor sind immer skalare Größen. So ist ja auch die Impulskomponente in x-, y- oder z-Richtung eine skalare Größe, die erst durch Zusammenfassung aller drei (bzw. vier, wenn wir die Energie dazunehmen) zu einem Vektor wird.
Zurück zur ursprünglichen Frage. vmax fragt, warum die Aufprallenergie unterschiedlich ist, wenn beide Autos sich aufeinander zubewegen bzw. wenn eines der Autos steht und das andere doppelt so schnell fährt. Meine Beschreibung erklärt den Unterschied mit der Bewegungsenergie nach der Kollision. Im ersten Fall ruht der Beobachter am Kollisionspunkt und es verbleibt nach der Kollision keine Bewegungsenergie übrig. Die gesamte Bewegungsenergie beider Fahrzeuge wurde in die Deformation umgesetzt. Im zweiten Fall bewegen sich die kollidierten Fahrzeuge relativ zum Beobachter weiter und haben genau die Bewegungsenergie, die vmax vermisst. Der in Deformation umgesetzte Anteil der Bewegungsenergie ist in beiden Fällen gleich, wie mein Beispiel zeigte. In der Praxis mag es übrigens geringe Unterschiede geben, weil beim Aufprall auf ein stehendes Fahrzeug eine Haftreibung überwunden werden muß. Ich denke aber, daß das getrost zu vernachlässigen ist.
Letztlich laufen beide Begründungen auf dasselbe hinaus. Meine Begründung unterscheidet einfach die beiden Fälle, während TomS Argumentation sich sicherlich mathematisch korrekt auf Transformationen beruft. Das scheint mir allerdings für das intuitive Verständnis (vorsichtig formuliert) ein Umweg zu sein. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 11. Dez 2015 10:21 Titel: Re: Elastischer/unelastischer Stoß jh8979 Verfasst am: 11. Dez 2015 10:21 Titel: Re: Elastischer/unelastischer Stoß |
 |
|
| MichaelK hat Folgendes geschrieben: | | Der Begriff „Skalar“ im Unterschied zu einem „Vektor“ bedeutet nach Wikipedia „…eine mathematische Größe, die allein durch die Angabe eines Zahlenwertes charakterisiert ist (in der Physik gegebenenfalls mit Einheit).“ In diesem Sinne ist die Energie, anders als beispielsweise die Geschwindigkeit oder der Impuls, ein Skalar. Die mechanische Energie eines bewegten Körpers, in diesem Falle des Autos, hat keine Richtung. Daran ändert auch die Tatsache nichts, daß die Energie in der Relativitätstheorie die Komponente eines Vektors ist. Komponenten eines Vektor sind immer skalare Größen. So ist ja auch die Impulskomponente in x-, y- oder z-Richtung eine skalare Größe, die erst durch Zusammenfassung aller drei (bzw. vier, wenn wir die Energie dazunehmen) zu einem Vektor wird. |
Auch wenn es ein Nebenschauplatz ist:
Den Begriff des Skalars in der Physik auf diese Weise zu verwenden ist grob fahrlässig und zeugt nicht von Verständnis. In der Physik ist die x-Komponente des Impulsvektors in der Regel kein Skalar. "Skalar" in der Physik bezieht sich immer auf eine Transformationsgruppe (in der Regel meint man bezüglich Rotationen oder bezüglich der Lorentzgruppe). So ist die kinetische Energie eine skalare Größe bezüglich Rotationen, aber nicht bezüglich Lorentz-Boosts; die x-Komponente des Impulses ist zwar nur eine Zahl, aber bezüglich keiner der beiden Gruppen ein Skalar (aber bezüglich Rotationen um die x-Achse schon). |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 11. Dez 2015 20:23 Titel: TomS Verfasst am: 11. Dez 2015 20:23 Titel: |
 |
|
@MichaelK: Die Wiederholung deiner Argumentation macht sie nicht wahrer, und das Zitieren eines schlechten Wikipedia-Artikels macht diesen nicht besser. Die dort genannte Definition des Begriffs Skalar ist extrem unpräzise. Meine Argumentation hat nichts mit rel. Mechanik und Lorentz-Transformationen zu tun, sie gilt auch nicht-rel. für die die Galilei-Transformation. Meine Argumentation bzgl. der Transformation erklärt den Sachverhalt präzise und korrekt. Deine Argumentation ist wenig hilfreich.
@jh8979: Danke für die Bestätigung. Ich fürchte nur, Michael wird es auch dir nicht glauben.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 11. Dez 2015 21:34 Titel: jh8979 Verfasst am: 11. Dez 2015 21:34 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
@jh8979: Danke für die Bestätigung. Ich fürchte nur, Michael wird es auch dir nicht glauben. |
Zum Glück ist die Frage der Verwendung des Begriffs Skalar in der Physik ja keine Glaubenssache  |
|
 |
Nescio

Anmeldungsdatum: 05.12.2015
Beiträge: 279
|
 Nescio Verfasst am: 11. Dez 2015 23:39 Titel: Nescio Verfasst am: 11. Dez 2015 23:39 Titel: |
 |
|
|
Leute, die Definition von Wikipedia zum Skalar ist korrekt. Das Wort was ihr eigentlich meint ist "invariant". |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 12. Dez 2015 00:09 Titel: jh8979 Verfasst am: 12. Dez 2015 00:09 Titel: |
 |
|
| Nescio hat Folgendes geschrieben: | | Leute, die Definition von Wikipedia zum Skalar ist korrekt. Das Wort was ihr eigentlich meint ist "invariant". |
"invariant" unter welcher Transformation? |
|
 |
Nescio

Anmeldungsdatum: 05.12.2015
Beiträge: 279
|
 Nescio Verfasst am: 12. Dez 2015 01:16 Titel: Nescio Verfasst am: 12. Dez 2015 01:16 Titel: |
 |
|
| jh8979 hat Folgendes geschrieben: | | "invariant" unter welcher Transformation? |
Galilei Transformation.
| TomS hat Folgendes geschrieben: | | Das bedeutet, dass die Energie (genauso wie Geschwindigkeit und Impuls) keine skalare Größen sind. |
Du meinst, dass die Energie (genauso wie Geschwindigkeit und Impuls) keine invarianten Größen sind (bezüglich Galilei Transformation). Das hat mit Skalar oder nicht Skalar gar nichts zu tun.
| TomS hat Folgendes geschrieben: | | Was ist die Definition einer skalaren Größe? Dass sie in allen Bezugsystemen denselben Wert hat. |
Nein, das ist die Definition einer invarianten Größe.
Ihr habt das Problem des TE alle richtig gelöst: Die freigesetzte Deformationsenergie ist in jedem Bezugssystem gleich, die Gesamtenergie ist in jedem Bezugssystem konstant, hat aber einen anderen Wert, ist also nicht invariant unter Galilei Transformation. Nur leider verwechselt ihr hier die Begriffe Skalar und Invariante. Lest euch mal beide Wikipedia Artikel dazu in Ruhe durch, dann versteht ihr es hoffentlich.
https://de.wikipedia.org/wiki/Invarianz
https://de.wikipedia.org/wiki/Skalar_%28Mathematik%29 |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
|
 |
Nescio

Anmeldungsdatum: 05.12.2015
Beiträge: 279
|
 Nescio Verfasst am: 12. Dez 2015 11:07 Titel: Nescio Verfasst am: 12. Dez 2015 11:07 Titel: |
 |
|
| Wikipedia hat Folgendes geschrieben: | | In physics, a scalar is a one-dimensional physical quantity, i.e. one that can be described by a single real number (sometimes signed, often with units), in other words a scalar is a physical quantity that only has magnitude but no direction, unlike (or as a special case of) vectors, tensors, etc. which are described by several numbers which characterize magnitude and direction and a vector can be defined as a physical quantity that has magnitude and direction. Formally, a scalar is unchanged by coordinate system rotations or reflections (in Newtonian mechanics), or by Lorentz transformations or space-time translations (in relativity). |
Hast du diesen Text einmal selber gelesen? Da steht, ein Skalar ist eine Größe, die im Gegensatz zum Vektor keine Richtung hat. Das ist natürlich gleichbedeutend mit einer Invarianz unter Koordinatendrehungen. Die Lorentz-Transformation in der SRT lässt sich mathematisch auch als Drehmatrix beschreiben, weshalb dort Lorentz-Skalar und Lorentz-Invariante gleichbedeutend sind. Die Galilei Transformation ist aber keine Drehung, deshalb ist eine Größe die invariant unter Galilei Transformation ist kein Skalar.
Falls du es jetzt immer noch nicht glaubst, dann lassen wir die Diskussion lieber bleiben.
freundliche Grüße
Nescio |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 12. Dez 2015 11:25 Titel: jh8979 Verfasst am: 12. Dez 2015 11:25 Titel: |
 |
|
| Nescio hat Folgendes geschrieben: | | Wikipedia hat Folgendes geschrieben: | | Formally, a scalar is unchanged by coordinate system rotations or reflections (in Newtonian mechanics), or by Lorentz transformations or space-time translations (in relativity). |
Hast du diesen Text einmal selber gelesen? Da steht, ein Skalar ist eine Größe, die im Gegensatz zum Vektor keine Richtung hat. Das ist natürlich gleichbedeutend mit einer Invarianz unter Koordinatendrehungen. Die Lorentz-Transformation in der SRT lässt sich mathematisch auch als Drehmatrix beschreiben, weshalb dort Lorentz-Skalar und Lorentz-Invariante gleichbedeutend sind. Die Galilei Transformation ist aber keine Drehung, deshalb ist eine Größe die invariant unter Galilei Transformation ist kein Skalar.
|
Ich hab nie behauptet, dass Galilei-Transformationen Drehungen sind, aber natürlich kann ich deren Invarianten genauso Skalar nennen. Üblicherweise meint man in der Regel allerdings Drehung- oder Lorentz-Invarianten, wenn man von einem Skalar spricht. Aber wenn Du Skalar bezüglich Galileitransformationen sagst, weiss auch jeder Physiker was das ist.
(Mal ganz davon abgesehen, dass die Galilei-Transformationen nur der v<<c Limes der Lorentztransformationen sind.)
Der Hauptpunkt der Diskussion war allerdings nicht Rotation/Lorentz/Galilei, sondern, dass in der Physik der Begriff "Skalar" etwas über Transformationseigenschaften aussagt und nicht einfach nur eine reale Zahl ist wie die Komponente eines Vektors. |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 12. Dez 2015 11:29 Titel: as_string Verfasst am: 12. Dez 2015 11:29 Titel: |
 |
|
Ich weiß nicht genau, welchen Wert es überhaupt hat, sich über Definitionen zu streiten. Aber wenn es hilft: auch ich kenne in der Physik die Definition von "Skalar" so wie es jh8979 und TomS hier wiedergeben.
Gruß
Marco |
|
 |
Nescio

Anmeldungsdatum: 05.12.2015
Beiträge: 279
|
 Nescio Verfasst am: 12. Dez 2015 11:37 Titel: Nescio Verfasst am: 12. Dez 2015 11:37 Titel: |
 |
|
Dann erklär doch mal, wie man ausgehend von eurer Definition eines Skalars auf diese Aussagen kommt.
| Wikipedia hat Folgendes geschrieben: | Examples in classical physics
Some examples of scalars include the mass, charge, volume, time, speed, temperature, or electric potential at a point inside a medium. The distance between two points in three-dimensional space is a scalar, but the direction from one of those points to the other is not, since describing a direction requires two physical quantities such as the angle on the horizontal plane and the angle away from that plane. Force cannot be described using a scalar, since force is composed of direction and magnitude, however, the magnitude of a force alone can be described with a scalar, for instance the gravitational force acting on a particle is not a scalar, but its magnitude is. The speed of an object is a scalar (e.g. 180 km/h), while its velocity is not (i.e. 180 km/h north). |
Warum sollte die Geschwindigkeit ein Skalar sein (bezüglich welcher Transformation überhaupt?). So wie ich euch verstehe meint ihr ja, dass ein Skalar einfach eine Invariante Größe ist. |
|
 |
MichaelK
Gast
|
 MichaelK Verfasst am: 12. Dez 2015 11:47 Titel: MichaelK Verfasst am: 12. Dez 2015 11:47 Titel: |
 |
|
Danke Nescio, das rückt mein Weltbild wieder zurecht.
Dennoch möchte ich jetzt die Argumentation der beiden Moderatoren verstehen. Auch der Link zum englischen Wikipedia beschreibt einen Skalar im physikalischen Sinne als "a one-dimensional physical quantity... unlike (or as a special case of) vectors, tensors, etc.". Darin erkenne ich noch keinen Unterschied zum "...broader concept also used in mathematics and computer science". Weiterhin stützt Wikipedia die Aussage, daß ein Skalar invariant gegenüber Koordinatentransformationen sei. Das ist aber etwas anderes als die Aussage, daß alle invarianten Größen Skalare genannt werden (freilich auch nicht unbedingt ein Widerspruch).
Wenn die Energie also nach TomS im physikalischen Sinne kein Skalar ist, muß sie ein Vektor oder Tensor sein und damit eine Richtung haben. Stimmt das und wohin zeigt sie denn dann? Und nochmal, wir reden von klassischer Newton'scher Mechanik. Mehr braucht man zur Beantwortung dieser Frage nicht zu bemühen.
Wie Nescio schon sagt, haben wir wohl alle "...das Problem des TE richtig gelöst". Ich denke wir sehen es nur jeweils auf einer unterschiedlichen Abstraktionsebene. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 12. Dez 2015 11:48 Titel: jh8979 Verfasst am: 12. Dez 2015 11:48 Titel: |
 |
|
| Nescio hat Folgendes geschrieben: |
Warum sollte die Geschwindigkeit ein Skalar sein (bezüglich welcher Transformation überhaupt?). So wie ich euch verstehe meint ihr ja, dass ein Skalar einfach eine Invariante Größe ist. |
Im Englischen gibt es zwei verschiedene Begriffe für Geschwindigkeit:
velocity = 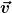
speed =  |
|
 |
MichaelK
Gast
|
 MichaelK Verfasst am: 12. Dez 2015 11:50 Titel: MichaelK Verfasst am: 12. Dez 2015 11:50 Titel: |
 |
|
|
...oh sorry, jetzt geht die Post ab. Mein letzter Beitrag bezog sich noch auf jh8979 von 10:44. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 12. Dez 2015 11:55 Titel: jh8979 Verfasst am: 12. Dez 2015 11:55 Titel: |
 |
|
| MichaelK hat Folgendes geschrieben: | Danke Nescio, das rückt mein Weltbild wieder zurecht.
|
Ich lass das mal unkommentiert ... 
| Zitat: |
Weiterhin stützt Wikipedia die Aussage, daß ein Skalar invariant gegenüber Koordinatentransformationen sei. Das ist aber etwas anderes als die Aussage, daß alle invarianten Größen Skalare genannt werden (freilich auch nicht unbedingt ein Widerspruch).
|
Invarianz unter Koordinatentransformationen ist in der Physik die Definition des Begriffs "Skalar".
| Zitat: |
Wenn die Energie also nach TomS im physikalischen Sinne kein Skalar ist, muß sie ein Vektor oder Tensor sein und damit eine Richtung haben. Stimmt das und wohin zeigt sie denn dann? Und nochmal, wir reden von klassischer Newton'scher Mechanik. Mehr braucht man zur Beantwortung dieser Frage nicht zu bemühen.
|
Nicht jede Größe ist Skala, Vektor, Tensor, etc. Insbesondere ist die Energie die Komponente eines Vierervektors und daher kein Skalar bezüglich Lorentztransformaitonen. In der Newtonschen Mechanik ist die Energie ein Skalar bezüglich Rotationen... ob das jetzt irgendwie erhellend ist, kannst Du selber entscheiden... |
|
 |
Nescio

Anmeldungsdatum: 05.12.2015
Beiträge: 279
|
 Nescio Verfasst am: 12. Dez 2015 11:57 Titel: Nescio Verfasst am: 12. Dez 2015 11:57 Titel: |
 |
|
| MichaelK hat Folgendes geschrieben: | | Die Energie ist selbstverständlich eine skalare Größe, schon allein weil die Masse skalar ist und das (Skalar-)Produkt zweier Vektoren (also v**2), wie der Name schon sagt, auch skalar ist. |
Das ist genau richtig und deckt sich mit der Definition von Wikipedia.
Die Masse hat keine Richtung und ist daher ein Skalar, das Skalarprodukt zweier Vektoren ist ein Skalar und deshalb ist die Energie auch ein Skalar.
| jh8979 hat Folgendes geschrieben: | | Aber in der Physik wird eine Größe, die invariant unter Koordinatentransformationen ist, "Skalar" genannt (welche Transformation genau gemeint sind, hängt vom Kontext ab). [...] Ich hab nie behauptet, dass Galilei-Transformationen Drehungen sind, aber natürlich kann ich deren Invarianten genauso Skalar nennen. |
Das ist es was ich bestreite, was du hier beschreibst ist einfach eine Invariante und kein Skalar.
| Zitat: | | Im Englischen gibt es zwei verschiedene Begriffe für Geschwindigkeit: |
Ganz genau, das eine hat Betrag und Richtung, das andere hat keine Richtung und ist deshalb ein Skalar.
| as_string hat Folgendes geschrieben: | | Ich weiß nicht genau, welchen Wert es überhaupt hat, sich über Definitionen zu streiten. |
Ok, ich dachte auch dass euch euer Fehler nach meinem ersten kleinen Post klar werden würde. Da das hier aber ausartet und nichts mehr mit der Fragestellung des TE zu tun hat, belasse ich es jetzt dabei.
Zuletzt bearbeitet von Nescio am 12. Dez 2015 12:06, insgesamt einmal bearbeitet |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 12. Dez 2015 12:06 Titel: jh8979 Verfasst am: 12. Dez 2015 12:06 Titel: |
 |
|
| jh8979 hat Folgendes geschrieben: | | Aber in der Physik wird eine Größe, die invariant unter Koordinatentransformationen ist, "Skalar" genannt (welche Transformation genau gemeint sind, hängt vom Kontext ab). |
| Nescio hat Folgendes geschrieben: |
Das ist es was ich bestreite, was du hier beschreibst ist einfach eine Invariante und kein Skalar.
...
Ok, ich dachte auch dass euch euer Fehler nach meinem ersten kleinen Post klar werden würde. Da das hier aber ausartet und nichts mehr mit der Fragestellung des TE zu tun hat, belasse ich es jetzt dabei. |
Das ist kein Fehler unsererseits, sondern Du weisst schlicht nicht was Physiker unter einem Skalar verstehen. |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 12. Dez 2015 12:08 Titel: as_string Verfasst am: 12. Dez 2015 12:08 Titel: |
 |
|
| Nescio hat Folgendes geschrieben: |
| as_string hat Folgendes geschrieben: | | Ich weiß nicht genau, welchen Wert es überhaupt hat, sich über Definitionen zu streiten. |
Ok, ich dachte auch dass euch euer Fehler nach meinem ersten kleinen Post klar werden würde. Da das hier aber ausartet und nichts mehr mit der Fragestellung des TE zu tun hat, belasse ich es jetzt dabei. |
Ich weiß nicht, warum Du von falsch oder richtig redest. Ich weiß auch nicht, warum Du irgendwie gereizt reagierst (so kommt es mir zumindest vor). Offenbar sind das eben unterschiedliche Definitionen des Begriffs "Skalar". Definitionen sind ja an sich nie falsch oder richtig, sie können nur konsistent oder widersprüchlich oder eindeutig oder sinnvoll oder nützlich sein oder eben nicht. So lange jeder in einer bestimmten Diskussion die selben Definitionen verwendet, ist ja alles gut...
Ich selbst ziehe daher aus diesem Thread nur den Schluss: offenbar sind unterschiedliche Definitionen des Begriffs "Skalar" gängig, deshalb muss man vorab immer sicher stellen, dass man in einer Diskussion auch von der selben ausgeht, wenn man diesen Begriff verwendet.
Gruß
Marco |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 12. Dez 2015 12:18 Titel: TomS Verfasst am: 12. Dez 2015 12:18 Titel: |
 |
|
| MichaelK hat Folgendes geschrieben: | ... der Link zum englischen Wikipedia beschreibt einen Skalar im physikalischen Sinne als "a one-dimensional physical quantity... unlike (or as a special case of) vectors, tensors, etc.".
Weiterhin stützt Wikipedia die Aussage, daß ein Skalar invariant gegenüber Koordinatentransformationen sei. |
Genau das hatte ich oben geschrieben, und genau darin liegt der Widerspruch bei Wikipedia.
Entweder bezeichne ich alle eindimensionale Größen als Skalare, ohne auf ihre Transformationseigenschaften einzugehen. Dann laufe ich spätestens bei der RT in Widersprüche zum üblichen Sprachgebrauch.
Oder ich bezeichne nur eindimensionale Größen mit jeweils definiertem Transformationsverhalten als Skalare. Dann tue ich aus Sicht der Newtonschen Mechanik des Guten zuviel, bin aber auf die RT, Feld- und Eichtheorien vorbereitet.
Die dritte Option, die Wikipedia gewählt hat, nämlich das irgendwie zu mischen, ist sicher Quatsch.
| MichaelK hat Folgendes geschrieben: | | Wenn die Energie also nach TomS im physikalischen Sinne kein Skalar ist, muß sie ein Vektor oder Tensor sein und damit eine Richtung haben. |
Nein, so ist das rein logisch nicht.
Wenn ich die Tierwelt in Hasen, Füchse und Grashüpfer aufteile, dann ist ein Aal nicht schon deswegen ein Fuchs oder ein Grashüpfer, weil er kein Hase ist :-)
Skalare, Vektoren und Tensoren haben jeweils ein definiertes Transformationsverhalten bzgl. einer bestimmten Transformationsgruppe. Die Energie ist ein Skalar bzgl. Rotationen und Translationen, jedoch nicht ggü. Galilei-Boosts. Damit ist sie jedoch noch kein Vektor oder Tensor, dazu müsst sie deren Eigenschaften haben.
In der NT habe ich mir noch gar nicht überlegt, wie man Objekte unter Boosts charakterisieren kann.
In der RT ist die Gesamtenergie ebenfalls weder ein Skalar noch ein Vektor, sie ist lediglich eine einzelne Komponente eines Vektors. Da die NT aus der RT im Grenzfall v/c = 0 hervorgeht, wäre die Gesamtenergie auch in der NT eine Komponente eines Vektors (allerdings muss man dann unüblicherweise mit der Gesamtenergie statt der kinetischen Energie rechnen).
Noch ein Beispiel: in der RT ist die kinetische Energie weder ein Skalar noch die Komponente eines Vektors, noch selbst ein Vektor. Sie ist lediglich eine nicht-invariante Größe.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 12. Dez 2015 12:32 Titel: TomS Verfasst am: 12. Dez 2015 12:32 Titel: |
 |
|
Vielleicht nochmal zurück zu meiner ursprünglichen Argumentation:
| Zitat: | Das bedeutet, dass die Energie ... keine skalare Größen ist.
Das ist auch der Grund, warum in der Hochenergiephysik eine andere invariante Größe genutzt wird, um den Prozess zu charakterisieren. |
Ich denke, an dieser Argumentation hat sich der Streit entzündet.
Meine Verwendung des Begriffs "skalar" im Kontext der Newtonschen Mechanik ist ungebräuchlich. Das ist jedoch Standard im Kontext der RT, auf die ich ja in der folgenden Argumentation eingehe.
Wenn man verstanden hat, dass "Lorentz-Skalar" für eine invariante Größe unter Lorentz-Transformation steht, dann kann man "XYZ-Skalar" auch für einen anderen Kontext mit XYZ-Symmetrie verwenden - und das tun die Physiker auch. Hier geht es eben um die Galilei-Invarianz.
D.h. die kinetische Energie ist keine Invariante Größe bzgl. allgemeiner Galilei-Transformationen, sie ist kein "Galilei-Skalar".
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
MichaelK
Gast
|
 MichaelK Verfasst am: 12. Dez 2015 12:34 Titel: MichaelK Verfasst am: 12. Dez 2015 12:34 Titel: |
 |
|
Also ich mag es garnicht, wenn sich "die Dinge am frühen morgen schon so dynamisch entwickeln". Nun kommt doch alle mal von dem Kindergartenniveau des "ich hab recht und Du hast unrecht" herunter.
Offensichtlich geht es doch um eine Frage, die völlig hinreichend mit klassischer Mechanik beantwortet werden kann. Aus jh8979s Antwort von 11:55 Uhr entnehme ich: "In der Newtonschen Mechanik ist die Energie ein Skalar bezüglich Rotationen". Für mich schließt sich damit der Kreis. Vielen Dank. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 12. Dez 2015 13:09 Titel: TomS Verfasst am: 12. Dez 2015 13:09 Titel: |
 |
|
| MichaelK hat Folgendes geschrieben: | | Nun kommt doch alle mal von dem Kindergartenniveau des "ich hab recht und Du hast unrecht" herunter. |
Ich habe versucht, sachlich und präzise zu argumentieren und auf Missverständnisse aufgrund unpräziser Argumentation hinzuweisen.
| MichaelK hat Folgendes geschrieben: | | Offensichtlich geht es doch um eine Frage, die völlig hinreichend mit klassischer Mechanik beantwortet werden kann. |
Stimmt, habe ich in meiner ersten Antwort auch getan.
| MichaelK hat Folgendes geschrieben: | | Aus jh8979s Antwort von 11:55 Uhr entnehme ich: "In der Newtonschen Mechanik ist die Energie ein Skalar bezüglich Rotationen". Für mich schließt sich damit der Kreis. Vielen Dank. |
Die Aussage von jh8979 ist völlig korrekt, trägt aber zur Beantwortung der ursprünglichen Frage nichts bei, da es sich nicht um Rotationen sondern um Boosts handelt (was von jh8979 aber auch nie anders behauptet wurde).
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 12. Dez 2015 13:21 Titel: index_razor Verfasst am: 12. Dez 2015 13:21 Titel: |
 |
|
Nur mal so als Bemerkung am Rande: man kann die relativistische Energie als Skalarprodukt zweier Vierervektoren schreiben, nämlich des Impulses des Teilchens (um dessen Energie es geht) und der Vierergeschwindigkeit des Beobachters (der die Energie mißt):

Beweist das nun, daß die Energie ein Skalar ist oder daß das Minkowskiprodukt nicht invariant unter Lorentztransformationen ist?
Es macht m.E. mehr Sinn, die Energie als invariante Größe zu betrachten, in deren Definition eben neben dem Teilchen noch ein weiteres geometrisches Objekt, nämlich der Beobachter, eingeht.
Dasselbe gilt übrigens für den Begriff Relativgeschwindigkeit in der Relativitätstheorie. Die Größe 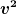 im Faktor im Faktor  etc. ist das Minkowskiprodukt etc. ist das Minkowskiprodukt  (oder dessen Negatives, je nach Vorzeichenkonvention) des Vierervektors (oder dessen Negatives, je nach Vorzeichenkonvention) des Vierervektors  mit sich selbst, der eindeutig durch die Gleichung mit sich selbst, der eindeutig durch die Gleichung
)
(hierbei sind u und w die Vierergeschwindigkeiten der Beobachter um deren Relativgeschwindigkeit es geht) und durch die Orthogonalität zur Vierergeschwindigkeit u definiert ist. Er gibt die Relativgeschwindigkeit von w gemessen von u an. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 12. Dez 2015 13:52 Titel: jh8979 Verfasst am: 12. Dez 2015 13:52 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | Nur mal so als Bemerkung am Rande: man kann die relativistische Energie als Skalarprodukt zweier Vierervektoren schreiben, nämlich des Impulses des Teilchens (um dessen Energie es geht) und der Vierergeschwindigkeit des Beobachters (der die Energie mißt):

Beweist das nun, daß die Energie ein Skalar ist oder daß das Minkowskiprodukt nicht invariant unter Lorentztransformationen ist?
|
Die Energie, die ein bestimmter Beobachter misst, ist in der Tat invariant (alle Beobachter stimmen darin überein, was der erste Beobachter misst). Die Energie des Objektes hingegen nicht (alle Beobachter messen was unterschiedliches).
| Zitat: |
Es macht m.E. mehr Sinn, die Energie als invariante Größe zu betrachten, in deren Definition eben neben dem Teilchen noch ein weiteres geometrisches Objekt, nämlich der Beobachter, eingeht.
|
Ich denken nicht, dass das i.A. vorteilhaft ist. So interessiert einen in der Regel die Energie, die Teilchen wirklich haben in verschiedenen Bezugsystemen und nicht nur die Energie, die es bezüglich eines bestimmten Beobachters hat. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 12. Dez 2015 14:24 Titel: TomS Verfasst am: 12. Dez 2015 14:24 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Nur mal so als Bemerkung am Rande: man kann die relativistische Energie als Skalarprodukt zweier Vierervektoren schreiben, nämlich des Impulses des Teilchens (um dessen Energie es geht) und der Vierergeschwindigkeit des Beobachters (der die Energie mißt) ... |
Das kann man tun, aber das ist eine andere, nicht-äquivalente Definition, und deshalb muss man dafür auch ein anderes Formelzeichen und einen anderen Begriff einführen!
Geht man aus vom Viererimpuls p eines Objektes
)
sowie der Vierergeschwindigkeit u eines Beobachters
)
so gilt
)
Wie man sieht stimmen die Definition der Energie E eines Objekte als Nullkomponente des Viererimpulses und der hier neu eingeführte Begriff i.A. nicht überein.
Wenn ich speziell mich selbst als Beobachter auszeichne, d.h. wenn ich für mich in meinem Ruhesystem u = (1,0) und v = 0 gilt, dann folgt
} = E)
Dieses E ist die Energie, die ich selbst diesem Objekt zuschreibe. Andere Beobachter mit anderem u schreiben dem Objekt eine andere Energie zu, alle stimmen jedoch mit mir bzgl. meiner Zuschreibung überein.
Nochmal zur Klarstellung:
Die relativistische Energie E ist die Nullkomponente eines Vierervektors. Der hier neu eingeführte Begriff ist ein Lorentz-Skalar. Erstere bezeichnet ganz allgemein die Energie bzgl. eines beliebigen Bezugsystems und ist daher bezugsystemabhängig. Letzteres bezeichnet die speziell von einem mittels u ausgezeichneten Beobachter gemessene Energie und ist daher beobachterabhängig. Ein anderer Beobachter mit anderem u misst eine andere Energie für das selbe Objekt. Aber alle Beobachter stimmen darin überein, dass dieser eine durch u ausgezeichnete Beobachter diese Energie misst.
Die Diskussion dieses neuen, inäquivalenten Begriffs ist sehr interessant, führt uns aber wohl noch weiter vom ursprünglichen Thema weg.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 12. Dez 2015 15:29 Titel: index_razor Verfasst am: 12. Dez 2015 15:29 Titel: |
 |
|
| jh8979 hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | Nur mal so als Bemerkung am Rande: man kann die relativistische Energie als Skalarprodukt zweier Vierervektoren schreiben, nämlich des Impulses des Teilchens (um dessen Energie es geht) und der Vierergeschwindigkeit des Beobachters (der die Energie mißt):

Beweist das nun, daß die Energie ein Skalar ist oder daß das Minkowskiprodukt nicht invariant unter Lorentztransformationen ist?
|
Die Energie, die ein bestimmter Beobachter misst, ist in der Tat invariant (alle Beobachter stimmen darin überein, was der erste Beobachter misst). Die Energie des Objektes hingegen nicht (alle Beobachter messen was unterschiedliches).
|
Aus diesem Grunde gibt es eben nicht "die" Energie eines Objektes, genauso wenig wie es "die" Geschwindigkeit gibt. Beides sind relative Begriffe, in deren Definition jeweils ein Beobachter eingeht.
| Zitat: |
| Zitat: |
Es macht m.E. mehr Sinn, die Energie als invariante Größe zu betrachten, in deren Definition eben neben dem Teilchen noch ein weiteres geometrisches Objekt, nämlich der Beobachter, eingeht.
|
Ich denken nicht, dass das i.A. vorteilhaft ist. So interessiert einen in der Regel die Energie, die Teilchen wirklich haben in verschiedenen Bezugsystemen und nicht nur die Energie, die es bezüglich eines bestimmten Beobachters hat. |
Die Energie, die sie "wirklich" in einem Bezugssystem haben, ist identisch mit der Energie, die ein Beobachter (oder Meßgerät) mißt, der in diesem Bezugssystem ruht. Du benötigst also nur den Beobachter, repräsentiert durch seine momentane Vierergeschwindigkeit. Das ist nicht weniger wirklich. Ein Bezugssystem mußt du nicht mal erwähnen. Wie gesagt, ich finde es klarer nur invariante Begriffe zu verwenden, und die Energie hat eine vollkommen natürliche invariante Definition.
Zuletzt bearbeitet von index_razor am 12. Dez 2015 17:33, insgesamt 2-mal bearbeitet |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 12. Dez 2015 15:50 Titel: index_razor Verfasst am: 12. Dez 2015 15:50 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Nur mal so als Bemerkung am Rande: man kann die relativistische Energie als Skalarprodukt zweier Vierervektoren schreiben, nämlich des Impulses des Teilchens (um dessen Energie es geht) und der Vierergeschwindigkeit des Beobachters (der die Energie mißt) ... |
Das kann man tun, aber das ist eine andere, nicht-äquivalente Definition, und deshalb muss man dafür auch ein anderes Formelzeichen und einen anderen Begriff einführen!
|
Nein, das ist genau dieselbe Definition und derselbe Begriff. Es ergeben sich nur zwei verschiedene Energiewerte, weil du zwei verschiedene Beobachter eingeführt hast: einen mit Vierergeschwindigkeit ) (bzgl. deines willkürlich gewählten Inertialsystems) und einen mit der Vierergeschwindigkeit (bzgl. deines willkürlich gewählten Inertialsystems) und einen mit der Vierergeschwindigkeit ) (bzgl. desselben Systems). (bzgl. desselben Systems).
Das was du als 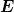 bezeichnest ist einfach bezeichnest ist einfach  . Dein . Dein  ist ist  . .
Man kann die Beziehung zwischen den beiden Vierergeschwindigkeiten wieder invariant mit Hilfe der Relativgeschwindigkeit ausdrücken, nämlich ) und erhält dann, wegen und erhält dann, wegen  deine Beziehung deine Beziehung
=\gamma(E-\vec{p}\cdot\vec{v}).)
(Beachte  , da es sich um raumartige Vektoren aus dem orthogonalen Komplement desselben Vierervektors w handelt.) , da es sich um raumartige Vektoren aus dem orthogonalen Komplement desselben Vierervektors w handelt.)
| Zitat: |
Nochmal zur Klarstellung:
Die relativistische Energie E ist die Nullkomponente eines Vierervektors. Der hier neu eingeführte Begriff ist ein Lorentz-Skalar.
|
Ich halte eben ersteres nicht für eine klare Definition. Sie impliziert ein sehr spezielles Koordinatensystem (ansonsten gibt es ja keine "Nullkomponente"), wo lediglich ein weiterer zeitartiger Vierervektor benötig wird. Dieser wird ja auch (als Zeitachse) in deinem impliziten Koordinatensystem benötigt.
| Zitat: |
Die Diskussion dieses neuen, inäquivalenten Begriffs ist sehr interessant, führt uns aber wohl noch weiter vom ursprünglichen Thema weg. |
Die Begriffe sind äquivalent. Der eine ist nur konzeptionell klarer. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 12. Dez 2015 17:47 Titel: TomS Verfasst am: 12. Dez 2015 17:47 Titel: |
 |
|
Die Begriffe sind nicht äquivalent!
Bei einem handelt es sich um die Nullkomponente eines Vierevektors, beim anderen um einen Skalar.
Ja, sie hängen miteinander zusammen, nein, sie sind nicht das selbe.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 12. Dez 2015 17:51 Titel: index_razor Verfasst am: 12. Dez 2015 17:51 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Die Begriffe sind nicht äquivalent!
Bei einem handelt es sich um die Nullkomponente eines Vierevektors, beim anderen um einen Skalar.
Ja, sie hängen miteinander zusammen, nein, sie sind nicht das selbe. |
Die Nullkomponente eines Vierervektors (bzgl. eines Inertialsystems) ist das Skalarprodukt des Vektors mit dem Einheitsvektor in Zeitrichtung. Diesen habe ich vorher 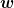 genannt. Dieser Einheitsvektor ist genau identisch mit der Vierergeschwindigkeit eines Beobachters, der im Ursprung dieses Inertialsystems ruht. Aus diesem Grund sind beide Begriffe absolut identisch. Der eine verzichtet nur auf überflüssige Konzepte, wie ein "Koordinatensystem mit Zeitachse". genannt. Dieser Einheitsvektor ist genau identisch mit der Vierergeschwindigkeit eines Beobachters, der im Ursprung dieses Inertialsystems ruht. Aus diesem Grund sind beide Begriffe absolut identisch. Der eine verzichtet nur auf überflüssige Konzepte, wie ein "Koordinatensystem mit Zeitachse". |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 12. Dez 2015 17:55 Titel: jh8979 Verfasst am: 12. Dez 2015 17:55 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: |
Die Nullkomponente eines Vierervektors (bzgl. eines Inertialsystems) ist das Skalarprodukt des Vektors mit dem Einheitsvektor in Zeitrichtung. Diesen habe ich vorher 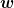 genannt. Dieser Einheitsvektor ist genau identisch mit der Vierergeschwindigkeit eines Beobachters, der im Ursprung dieses Inertialsystems ruht. genannt. Dieser Einheitsvektor ist genau identisch mit der Vierergeschwindigkeit eines Beobachters, der im Ursprung dieses Inertialsystems ruht. |
Entweder dein w ist ein fester Lorentzvektor, dann ist Dein Skalarprodukt damit nicht Lorentz-invariant, oder es ist ein normaler Lorentzvektor, dann liefert das Skalarprodukt nicht in jedem Bezugssystem die Nullkomponente des Vierervektors... daher sind es zwei verschiedene Begriffe wie Tom schon gesagt hat (in einem Bezugssystem stimmen sie allerdings überein, aber nur in einem). |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 12. Dez 2015 18:04 Titel: index_razor Verfasst am: 12. Dez 2015 18:04 Titel: |
 |
|
| jh8979 hat Folgendes geschrieben: |
Entweder dein w ist ein fester Lorentzvektor, dann ist Dein Skalarprodukt damit nicht Lorentz-invariant, oder es ist ein normaler Lorentzvektor, dann liefert das Skalarprodukt nicht in jedem Bezugssystem die Nullkomponente des Vierervektors... daher sind es zwei verschiedene Begriffe wie Tom schon gesagt hat (in einem Bezugssystem stimmen sie allerdings überein, aber nur in einem). |
Definiere mal den Unterschied zwischen "festen" und "normalen" Vektoren. Im Minkowskiraum -- genauso übrigens wie im euklidischen Raum -- gibt es nur eine Art von Vektor. Mit je vier linear unabhängigen kann man ein Koordinatensystem aufspannen. Das Skalarprodukt mit w liefert in jedem System, welches w als Zeitachse verwendet die Nullkomponente jedes Vektors in diesem System. Das ist eine Trivialität bzw. die Definition von "Nullkomponente". Für die Definition der Energie ist das allerdings vollkommen irrelevant. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 12. Dez 2015 20:17 Titel: jh8979 Verfasst am: 12. Dez 2015 20:17 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: |
Definiere mal den Unterschied zwischen "festen" und "normalen" Vektoren. Im Minkowskiraum -- genauso übrigens wie im euklidischen Raum -- gibt es nur eine Art von Vektor. |
Ich weiss nicht, ob das hier noch irgendwie zielführend ist, da wir uns denk ich nicht in der Physik oder Mathematik uneinig sind und es letztendlich nur um Definitionen und deren Nützlichkeit geht.
Der Vollständigkeit halber, was ich meinte was:
1. Die Energie E eines Teilchens (so wie üblich definiert) mit Viererimpuls p ist in jedem Bezugsystem B definiert durch  , wobei u der "feste Vektor" (1,0,0,0) ist. "Fest" heist hier, dass er in allen Bezugsystemen die Form (1,0,0,0) hat (also ist er kein Lorentz-Vektor, insofern ist meine Bezeichnung vllt etwas verwirrend, aber das ist die übliche Bezeichnung z.B. in HQET, in der genau dieser "feste Vektor" auftritt). Diese Energie EB ist offensichtlich kein Lorentz-Skalar, sondern vom Bezugsystem abhängig, insbesondere ist EB immer die Null-Komponente eines Vierervektors im Bezugsystem B. , wobei u der "feste Vektor" (1,0,0,0) ist. "Fest" heist hier, dass er in allen Bezugsystemen die Form (1,0,0,0) hat (also ist er kein Lorentz-Vektor, insofern ist meine Bezeichnung vllt etwas verwirrend, aber das ist die übliche Bezeichnung z.B. in HQET, in der genau dieser "feste Vektor" auftritt). Diese Energie EB ist offensichtlich kein Lorentz-Skalar, sondern vom Bezugsystem abhängig, insbesondere ist EB immer die Null-Komponente eines Vierervektors im Bezugsystem B.
2. Wenn ich Dich richtig verstanden hab, möchtest Du nun lieber folgendes machen: Die "index_razor"-Energie e eines Teilchens bezüglich eines Beobachter S (wie speziell) ist definiert durch  , wobei w der Lorentz-Vektor, welcher die Zeitachse von B festlegt. Diese Energie eS ist ein Lorentz-Skalar, da w ein Lorentz-Vektor ist. Falls B=S gilt offensichtlich EB=eS, ansonsten natürlich nicht. , wobei w der Lorentz-Vektor, welcher die Zeitachse von B festlegt. Diese Energie eS ist ein Lorentz-Skalar, da w ein Lorentz-Vektor ist. Falls B=S gilt offensichtlich EB=eS, ansonsten natürlich nicht.
Ich denk soweit sind wir uns einig (ausser, dass Dir vllt meine Bezeichnung "fester Vektor" nicht gefällt). Es geht dann also nur um die Frage ob es einen Vorteil hat eS statt EB zu verwenden. Ich seh nicht so recht, wieso das (praktisch und konzeptionell) besser sein sollte, aber das mag auch nur meine persönliche Meinung sein. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 13. Dez 2015 01:16 Titel: TomS Verfasst am: 13. Dez 2015 01:16 Titel: |
 |
|
Doch, ich sehe die Vorteile schon, und ich kenne auch Beispiele, wo dies genau so verwendet wird.
Aber die Vorteile resultieren gerade daraus, dass es sich um eine andere Größe handelt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 13. Dez 2015 08:06 Titel: index_razor Verfasst am: 13. Dez 2015 08:06 Titel: |
 |
|
| jh8979 hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: |
Definiere mal den Unterschied zwischen "festen" und "normalen" Vektoren. Im Minkowskiraum -- genauso übrigens wie im euklidischen Raum -- gibt es nur eine Art von Vektor. |
Ich weiss nicht, ob das hier noch irgendwie zielführend ist, da wir uns denk ich nicht in der Physik oder Mathematik uneinig sind und es letztendlich nur um Definitionen und deren Nützlichkeit geht.
|
Ich denke es geht um mehr als nur Definitionen und Nützlichkeit, aber sehen wir mal.
| Zitat: |
Der Vollständigkeit halber, was ich meinte was:
1. Die Energie E eines Teilchens (so wie üblich definiert) mit Viererimpuls p ist in jedem Bezugsystem B definiert durch  , wobei u der "feste Vektor" (1,0,0,0) ist. "Fest" heist hier, dass er in allen Bezugsystemen die Form (1,0,0,0) hat (also ist er kein Lorentz-Vektor, insofern ist meine Bezeichnung vllt etwas verwirrend, aber das ist die übliche Bezeichnung z.B. in HQET, in der genau dieser "feste Vektor" auftritt). , wobei u der "feste Vektor" (1,0,0,0) ist. "Fest" heist hier, dass er in allen Bezugsystemen die Form (1,0,0,0) hat (also ist er kein Lorentz-Vektor, insofern ist meine Bezeichnung vllt etwas verwirrend, aber das ist die übliche Bezeichnung z.B. in HQET, in der genau dieser "feste Vektor" auftritt).
|
Also handelt es sich nicht um einen Vektor u, sondern um die Menge aller Vektoren, die kollinear zur Zeitachse irgendeines Inertialsystems sind. Für zwei gegeneinander geboostete Systeme ergeben sich so verschiedene Vektoren. Die Menge dieser Vektoren ist identisch mit der Menge aller normierten, zeitartigen und zukunftsgerichteten Vektoren, also der Menge aller möglichen Vierergeschwindigkeiten.
Du bezeichnest also letztendlich eine Menge von Vektoren u, als "einen nicht-lorentzinvarianten Vektor" und die Skalarprodukte eines Vektors p mit jedem Element dieser Menge als "eine Zahl, die kein Lorentz-Skalar ist", obwohl es sich schlicht um viele verschiedene Skalare handelt.
Das ist genau das, was ich an "konzeptioneller Unklarheit" bemängele. Konzeptionell unterscheidet sich der Minkowskiraum von einem euklidischen Raum nur durch die Indefinitheit seiner Metrik. Bist du irgendwo in der euklidischen Geometrie gezwungen zwischen dreh-invarianten und nicht-invarianten Vektoren und Winkeln zu unterscheiden?
Ich denke der Hintergrund dafür ist, daß du nicht deutlich zwischen einem Vektor x und seinem Komponententupel (1,0,0,0) unterscheidest und nicht klar wird, daß hinter letzterem immer eine Basis steht, weil diese nirgendwo ausdrücklich erwähnt ist. Ich kann nicht sowohl den Vektor x als auch sein Tupel fest halten, wenn ich die Basis lorentztransformiere.
| Zitat: |
2. Wenn ich Dich richtig verstanden hab, möchtest Du nun lieber folgendes machen: Die "index_razor"-Energie e eines Teilchens bezüglich eines Beobachter S (wie speziell) ist definiert durch  , wobei w der Lorentz-Vektor, welcher die Zeitachse von B festlegt. Diese Energie eS ist ein Lorentz-Skalar, da w ein Lorentz-Vektor ist. Falls B=S gilt offensichtlich EB=eS, ansonsten natürlich nicht. , wobei w der Lorentz-Vektor, welcher die Zeitachse von B festlegt. Diese Energie eS ist ein Lorentz-Skalar, da w ein Lorentz-Vektor ist. Falls B=S gilt offensichtlich EB=eS, ansonsten natürlich nicht.
|
w ist die Vierergeschwindigkeit des Beobachters S und damit kollinear zur Zeitachse irgendeines Systems (von mir aus B), ja. B spielt allerdings überhaupt keine Rolle, nur S und w. Es handelt sich bei w also um einen der Vektoren aus der Menge deren Gesamtheit du oben als "keinen Lorentz-Vektor" bezeichnet hast. Sein Skalarprodukt mit p ist eines der Skalarprodukte, deren Gesamtheit du oben als "keinen Lorentz-Skalar" bezeichnet hast. Lediglich erwähne ich keine Inertialsysteme, keine Komponententupel und führe nicht Begriffe wie "Nicht-Lorentzvektor" für eine Menge von Lorentzvektoren und "Nicht-Lorentz-Skalar" für eine Menge von Skalaren ein.
Ich muß überhaupt keine verschiedenen Arten von Vektoren und Zahlen unterscheiden. w, p, u sind alles völlig gleichartige und gleichberechtigte Vektoren des Minkowskiraums, aus denen ich beliebige Skalarprodukte bilden kann, z.B. 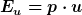 oder oder  . Deswegen halte ich das für das bessere Konzept, obwohl es natürlich nur eine Energie gibt, von der letztendlich beide Sichtweisen sprechen. . Deswegen halte ich das für das bessere Konzept, obwohl es natürlich nur eine Energie gibt, von der letztendlich beide Sichtweisen sprechen.
Zuletzt bearbeitet von index_razor am 13. Dez 2015 09:37, insgesamt einmal bearbeitet |
|
 |
|
|
















