| Autor |
Nachricht |
MarlonBND
Gast
|
 MarlonBND Verfasst am: 23. Jul 2023 07:37 Titel: Beschleunigung am zweiseitigen Hang |
 |
|
Meine Frage:
Hallo,
zwei Massen sind mit einer Seilrolle verbunden und hängen auf verschiedenen Seiten einer schiefen Ebene mit verschiedenen Neigungswinkeln. Gesucht ist unter anderem die Beschleunigung in Richtung der 1. Masse.
Leider habe ich keine Möglichkeit gefunden Bilder einzufügen. Wenn man allerdings bei google Bildersuche "zweiseitiger hang physikaufgabe" eingibt, ist das erste Bild die passende Skizze.
Meine Ideen:
Mein Ansatz:
F_{res}=F_{m1}-F_{m2}
führt zu:
(m_{1}-m_{2}) \cdot a=m_{1}g\sin(\alpha )- m_{2}g\sin(\beta )
und ist bis auf das Minuszeichen richtig. Laut Musterlösung muss folgendes rauskommen:
(m_{1}+m_{2}) \cdot a=m_{1}g\sin(\alpha )- m_{2}g\sin(\beta )
Das verstehe ich aber überhaupt nicht, meiner Meinung nach ist doch die Differenz der Massen und nicht die Summe der Massen für die Beschleunigung verantwortlich. Kann mir bitte jemand bei meinem (Denk-) Fehler helfen?
|
|
 |
marlonbnd
Anmeldungsdatum: 23.07.2023
Beiträge: 25
|
| marlonbnd Verfasst am: 23. Jul 2023 07:52 Titel: Formeln einfügen |
|
|
PS: Wiese werden meine Formeln nicht angezeigt? Bzw. kann mir jemand sagen, wie ich das:
F_{res}=F_{m1}-F_{m2}
als Formel anzeigen lasse.
PPS: Ich habe meine Lösung nochmal als Anhang hochgeladen. Mit rot habe ich aus dem Minus ein Plus gemacht so wie es sein soll. Ich verstehe aber eben nicht warum da ein Plus hin soll (siehe oben).
| Beschreibung: |
|
Download |
| Dateiname: |
Hang.JPG |
| Dateigröße: |
161.41 KB |
| Heruntergeladen: |
58 mal |
Zuletzt bearbeitet von marlonbnd am 23. Jul 2023 08:01, insgesamt 2-mal bearbeitet |
|
|
marlonbnd
Anmeldungsdatum: 23.07.2023
Beiträge: 25
|
| marlonbnd Verfasst am: 23. Jul 2023 07:57 Titel: Passendes Bild |
|
|
Hier nochmal das Bild zu der Aufgabe.
| Beschreibung: |
|
Download |
| Dateiname: |
Hang_Bild.JPG |
| Dateigröße: |
76.54 KB |
| Heruntergeladen: |
53 mal |
|
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5875
|
| Myon Verfasst am: 23. Jul 2023 08:41 Titel: |
|
|
Willkommen in diesem Forum!
Zuerst zu den nicht korrekt angezeigten Formeln: diese musst Du wie folgt mit Tags umgeben:
| Code: | | [latex]a^2+b^2=c^2[/latex] |
Zum Pluszeichen im Nenner: in der Gleichung
a=m_1g\sin\alpha-m_2g\sin\beta)
stehen auf der rechten Seite die Kräfte, welche am gesamten System, bestehend aus den beiden Massen, in der jeweiligen Bewegungsrichtung angreifen. Das Minuszeichen, da die Kräfte in entgegengesetzte Richtung wirken.
Auf der linken Seite hingegen steht die gesamte Masse des Systems. Sie gibt die Trägheit an, mit der sich das System gegen eine Beschleunigung sträubt. Je höher die Gesamtmasse, umso tiefer die Beschleunigung bei gleichen Kräften auf der rechten Seite.
Vgl. das zweite Newtonsche Gesetz:
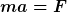
Rechts die auf den Körper mit Masse m wirkende Kraft, links die (träge) Masse des Körpers und die auftretende Beschleunigung.
|
|
|
marlonbnd
Anmeldungsdatum: 23.07.2023
Beiträge: 25
|
| marlonbnd Verfasst am: 23. Jul 2023 10:57 Titel: |
|
|
Vielen Dank! Das war mir nicht bekannt. Ist es dann so, dass sobald ich eine beschleunigte Bewegung habe, es eine Trägheitskraft der Größe Gesamtmasse mal die Beschleunigung existiert und ich diese abziehen muss?
Zu dem zweiten Satz von Newton:
„Wirkt auf einen Körper eine Kraft, so wird er in Richtung der Kraft beschleunigt. Die Beschleunigung ist dabei direkt proportional zur Kraft und indirekt proportional zur Masse des Körpers."
Dieser Satz wirft bei mir mehr Fragen auf als er beantwortet. Hier steht doch indirekt proportional zur Masse des Körpers. Dann wäre doch weniger Masse, weniger Kraft, aber das stimmt doch nicht.
Sorry für die vermutlich naiven Fragen, aber ich bin eigentlich Mathematiker und fuchse mich gerade als Unterstützung für meinen Sohn (aber auch als Hobby weil es Spaß macht) in das Thema ein....
|
|
|
marlonbnd
Anmeldungsdatum: 23.07.2023
Beiträge: 25
|
| marlonbnd Verfasst am: 23. Jul 2023 11:47 Titel: |
|
|
Im gleichem Zusammenhang: In der c) soll man die Seilkraft im Seil an Masse 1 bestimmen. Mein Ansatz war:
Hangabtriebskraft-Seilkraft = Trägheitskraft
Richtig ist aber
Hangabtriebskraft+Seilkraft = Trägheitskraft
Wieso?
Im Anhang ist meine Lösung, das Ergebnis ist dann bis auf das Minuszeichen identisch, aber doch von der Idee ganz anders. In meiner Vorstellung muss doch die Seilkraft der Kraft nach unten entgegenwirken?!
| Beschreibung: |
|
Download |
| Dateiname: |
Seilkraft.JPG |
| Dateigröße: |
202.8 KB |
| Heruntergeladen: |
51 mal |
|
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5875
|
| Myon Verfasst am: 23. Jul 2023 13:25 Titel: |
|
|
| marlonbnd hat Folgendes geschrieben: | | Ist es dann so, dass sobald ich eine beschleunigte Bewegung habe, es eine Trägheitskraft der Größe Gesamtmasse mal die Beschleunigung existiert und ich diese abziehen muss? |
Man kann dies so sehen. Das wäre eine Trägheitskraft nach d'Alembert, wodurch sich dann die Summe aller auf einen Körper wirkenden Kräfte zu null summieren:
Ich persönlich konnte mit diesem Konzept nie viel anfangen, wahrscheinlich einfach, weil ich es nie so gelernt habe. Ich würde in der Gleichung
die linke Seite als Wirkung/Folge der Kräfte sehen, die auf den Körper wirken. Als Folge der einwirkenden Kräfte tritt die Beschleunigung a auf. Auf der rechten Seite stehen "echte" Kräfte, die letztendlich immer auf einer der vier grundlegenden Wechselwirkungen, im Alltag Gravitation und elektromagnetische Wechselwirkung, beruhen. Einzig in nicht-Inertialsystemen muss man zusätzlich sg. Scheinkräfte wie die Zentrifugalkraft einführen, damit die Gleichung erfüllt ist.
| Zitat: | | „Wirkt auf einen Körper eine Kraft, so wird er in Richtung der Kraft beschleunigt. Die Beschleunigung ist dabei direkt proportional zur Kraft und indirekt proportional zur Masse des Körpers." |
Indirekt proportional einfach, weil a=F/m. Bei einer festen Kraft ist die Beschleunigung umso geringer, je grösser die Masse.
| Zitat: | Richtig ist aber
Hangabtriebskraft+Seilkraft = Trägheitskraft |
Nein, die Seilkraft zieht den Körper hangaufwärts, entgegen der Hangabtriebskraft.
Betrachtet man nur die Masse m1 und die Kräftte, die auf diese Masse wirken, so gilt also
Die Vorzeichen hängen davon ab, welche Richtung man als "positiv" festlegt. Die Vorzeichen der Kräfte müssen aber auf jeden Fall verschieden sein.
Setzt man für a die schon bestimmte Beschleunigung ein, ergibt sich
)
Unabhängig von der Vorzeichenwahl muss die Seilkraft positiv sein.
Zuletzt bearbeitet von Myon am 24. Jul 2023 20:39, insgesamt einmal bearbeitet |
|
|
marlonbnd
Anmeldungsdatum: 23.07.2023
Beiträge: 25
|
| marlonbnd Verfasst am: 24. Jul 2023 08:23 Titel: Problem gelöst |
|
|
Vielen Dank!
So macht das Sinn.
|
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5867
Wohnort: jwd
|
| Mathefix Verfasst am: 24. Jul 2023 16:37 Titel: |
|
|
@Myon
)
Da ist irgendwie das "g" verschwunden.
Hängt die Bewegungsrichtung nicht vom Verhältnis m_1 *sin(alpha)/m_2*sin (beta) ab?
|
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5875
|
| Myon Verfasst am: 24. Jul 2023 20:42 Titel: |
|
|
| Mathefix hat Folgendes geschrieben: | | Da ist irgendwie das "g" verschwunden. |
Ja stimmt, danke. Habe das oben noch eingefügt.
| Zitat: | | Hängt die Bewegungsrichtung nicht vom Verhältnis m_1 *sin(alpha)/m_2*sin (beta) ab? |
Ja, je nach dem Verhältnis der Hangabtriebskräfte erfolgt die Beschleunigung in die eine oder andere Richtung.
|
|
|
|
Registrieren
Login
FAQ
Suchen
