| Autor |
Nachricht |
manuel459
Anmeldungsdatum: 11.10.2016
Beiträge: 263
|
 manuel459 Verfasst am: 03. März 2021 15:52 Titel: Inertialsysteme manuel459 Verfasst am: 03. März 2021 15:52 Titel: Inertialsysteme |
 |
|
Hallo an alle,
ich habe Verständnisschwierigkeit wenn es um Inertialsysteme geht.
Dabei ist die klassische Definition ja die, dass sich kräftefreie Körper in Inertialsystemen gleichförmig geradlinig bewegen. Das trifft zum Beispiel bei einem Zug (konstante Geschwindigkeit) zu, da sich hier auch die Gravitationskraft mit der Bodenkraft quasi aufhebt und so Kräftefreiheit herrscht.
Nun habe ich (Einführung in die ART) gelernt, dass die Gravitation als Scheinkraft verstanden werden sollte und im freien Fall Kräftefreiheit herrscht (aus Newtonscher Sichtweise würde Bezugssystem und man selbst gravitativ beschleunigt werden, aus Einsteinscher Sichtweise transformiert sich die Gravitationskraft gerade weg).
Nun ist mir unklar, ob Inertialsysteme nun über diesen Newtonschen Zugang (Kräftefreiheit wobei Gravitation auch eine "äußere Kraft" ist) oder über den Einsteinschen Zugang definiert werden (Kräftefreiheit quasi bis auf Gravitation, da diese keine "äußere Kraft" ist).
Das macht nämlich dann einen Unterschied, ob man den Zug als Inertialsystem betrachtet oder nicht. Laut Newton wäre es ein Inertialsystem, laut Einstein aber nicht, da dort praktisch die Bodenkraft wirkt (und die Gravitation nicht gezählt wird).
Kann mir da jemand meinen Knoten im Kopf finden und lösen? Oder ist es womöglich eine Definitionssache?
Vielen Dank im Voraus und lG |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 03. März 2021 17:32 Titel: Re: Inertialsysteme DrStupid Verfasst am: 03. März 2021 17:32 Titel: Re: Inertialsysteme |
 |
|
| manuel459 hat Folgendes geschrieben: | | Nun ist mir unklar, ob Inertialsysteme nun über diesen Newtonschen Zugang (Kräftefreiheit wobei Gravitation auch eine "äußere Kraft" ist) oder über den Einsteinschen Zugang definiert werden (Kräftefreiheit quasi bis auf Gravitation, da diese keine "äußere Kraft" ist). |
Das kommt darauf an in welcher Theorie Du Dich bewegst und falls es die Newtonsche Meschanik ist, welche Systeme Du beschreiben willst. |
|
 |
manuel459
Anmeldungsdatum: 11.10.2016
Beiträge: 263
|
 manuel459 Verfasst am: 03. März 2021 17:36 Titel: manuel459 Verfasst am: 03. März 2021 17:36 Titel: |
 |
|
|
das bedeutet es gibt also verschiedene Definitionen von "Inertialsystem" ? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 03. März 2021 17:48 Titel: TomS Verfasst am: 03. März 2021 17:48 Titel: |
 |
|
Ja, weil es unterschiedliche Definitionen von "kräftefrei" und "geradlinig gleichförmig" gibt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
A.T.
Anmeldungsdatum: 06.02.2010
Beiträge: 343
|
 A.T. Verfasst am: 04. März 2021 09:12 Titel: A.T. Verfasst am: 04. März 2021 09:12 Titel: |
 |
|
| manuel459 hat Folgendes geschrieben: | | das bedeutet es gibt also verschiedene Definitionen von "Inertialsystem" ? |
Ja, und in der ART sind Inertialsysteme in einen räumlich variablen Gravitationsfeld nur lokale Approximationen. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 04. März 2021 10:45 Titel: TomS Verfasst am: 04. März 2021 10:45 Titel: |
 |
|
Noch eine Anmerkung zu "kräftefrei" und "geradlinig gleichförmig".
In der Newtonsche Mechanik gilt
 )
v und F bezeichnen Vektoren.
Bei Newton kann die Kraft sowohl die Gravitationskraft als auch weitere elektrische, magnetische usw. Kräfte enthalten.
Dabei steht rechts die Kraft, die links zu einer Beschleunigung und damit einer Abweichung von einer geradlinig gleichförmigen Bewegung führt. Umgekehrt verschwindet die Beschleunigung falls die Kraft verschwindet, womit die Bewegung geradlinig gleichförmig ist.
In der Allgemeine Relativitätstheorie könnte man schreiben
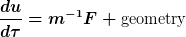
tau bezeichnet jetzt die Eigenzeit, nicht - wie bei Newton - die Koordinatenzeit t. u und F bezeichnen die 4er-Geschwindigkeit sowie die 4er-Kraft in der 4-dim. Raumzeit. Aus dieser Formulierung folgt in einer gewissen Näherung die o.g. Newtonsche Bewegungsgleichungen einschließlich der bekannten Gravitationskraft.
Aber so schreibt das niemand!
Die rechte Seite enthält einen rein geometrischen Term, der ausschließlich aus der Krümmung der Raumzeit (oder ungeschickten Koordinatensystemen) folgt und keine weiteren elektrischen, magnetischen usw. Felder enthält. Diesen rein geometrischen Term bringt man auf die linke Seite und erhält
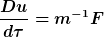
Die Ableitung ist dabei ein kompliziertes Objekt, das im Wesentlichen die Abweichung von einer Geodäten beschreibt. Eine Geodäte ist die Verallgemeinerung einer "geraden Linie" bzw. einer "kürzesten Linie zwischen zwei Punkten" in einer gekrümmten Raumzeit.
Was wir als Bahnkurven wahrnehmen ist die Projektion der Kurve in der 4-dim. Raumzeit in den 3-dim. Raum. So entstehen z.B. die (näherungsweise) elliptischen Bahnen der Planeten aus diesen 4-dim. Bahnkurven.
Damit ist - bis auf die kompliziertere Struktur der Ableitung - die Formulierung bei Newton und Einstein identisch: Eine kräftefreie Bewegung entspricht einer Bewegung entlangt einer Geodäten. Bei Newton kann man Geodäte durch Gerade ersetzen.
D.h. aber, dass bei Einstein die Gravitationskraft als solche verschwunden ist; sie ist implizit in der Geometrie enthalten.
D.h. auch, dass der Kraftbegriff bei Einstein wesentlich natürlicher ist Die Bewegung entlang einer Geodäten ist nicht nur mathematisch kräftefrei, sie ist es auch physikalisch, real messbar: im freien Fall spüre ich keine Kraft. Damit ist die Gravitationskraft bei Newton ein Artefakt, den ich nicht spüren kann, den ich jedoch benötige, um die mathematische Form der Bahnkurven zu beschreiben. Bei Einstein erscheint das völlig normal: wo ich keine Kraft spüre, die Bewegung also für mich kräftefrei ist, da existiert auch keine Kraft.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
manuel459
Anmeldungsdatum: 11.10.2016
Beiträge: 263
|
 manuel459 Verfasst am: 04. März 2021 16:29 Titel: manuel459 Verfasst am: 04. März 2021 16:29 Titel: |
 |
|
Vielen Dank! Jetzt wird das ganze für mich etwas klarer - ich muss zugeben diese Gedanken sind relativ neu für mich.
Ich versuche mich einmal an einer (von mir erstellten) Definition eines Inertialsystems - wäre toll wenn jemand seinen Senf dazugeben kann! 
Also ich definiere Inertialsysteme als Bezugssysteme, in denen der Trägheitssatz gilt. Dieser lautet "kräftefreie Körper bewegen sich geradlinig gleichförmig".
Hier wird aber nicht definiert, was "geradlinig gleichförmig" bedeutet, sondern man muss vorher schon wissen, was das bedeutet. Newton meint damit "Geraden" im Sinne der euklidischen Geometrie. Einstein meint Geodäten im Minkowski Raum).
Die Definition des Inertialsystems ist in der Formulierung dieselbe (in beiden Theorien), man muss sie aber anders interpretieren.
Betrachtet man laut Newton die Gravitationskraft nicht als Scheinkraft oder Trägheitskraft, so ist der besagte Zug nur "horizontal" ein Inertialsystem, da "Kräftefreiheit" eine vertikale Bewegung nicht zulassen würde - wegen der Gravitationskraft die ja wirkt.
Einstein sieht die Gravitationskraft als Scheinkraft (also nicht als "äußere Kraft") und würde den Zug daher nicht als horizontales Inertialsystem sehen, da stets die Bodenkraft wirkt (und durch keine andere äußere Kraft aufgehoben wird).
Somit sind bei Einstein Inertialsysteme nur solche, die entweder fernab jeder Gravitation im Weltraum "schweben" oder frei fallende Bezugssysteme (die aber ausreichend "klein" sind - wegen der Lokalität der ART).
Mir drängt sich nach diesem Text irgendwie noch die Frage auf, ob ein frei fallendes Bezugssystem (lokal) in Newton's Sinne ein Inertialsystem wäre. Ich würde sagen ja, weil darin kräftefreie Körper (und im Bezugssystem weiß man ja nicht dass hier die Gravitation am Werk ist) sich geradlinig gleichförmig bewegen. - diese letzte Erklärung ist wieder nicht aus Einsteinscher Sicht, aber ich kann es in Einsteinscher Sprechweise irgendwie nicht ausdrücken.
Wärt ihr damit so zufrieden? Ich denke ich habs verstanden...
lG |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 04. März 2021 16:57 Titel: DrStupid Verfasst am: 04. März 2021 16:57 Titel: |
 |
|
| manuel459 hat Folgendes geschrieben: | | Betrachtet man laut Newton die Gravitationskraft nicht als Scheinkraft oder Trägheitskraft, so ist der besagte Zug nur "horizontal" ein Inertialsystem, da "Kräftefreiheit" eine vertikale Bewegung nicht zulassen würde - wegen der Gravitationskraft die ja wirkt. |
Der Zug selbst ist gundsätzlich kein Inertialsystem, aber sein Ruhesystem kann eines sein (wenn man von der Erdrotation absieht). Das gilt auch in vertikaler Richtung. Dass sich kräftefreie Körper in einem Inertialsystem auf Geodäten bewegen, heißt schließlich nicht, dass notwendigerweise alle Körper kräftefrei sein müssen.
| manuel459 hat Folgendes geschrieben: | | Mir drängt sich nach diesem Text irgendwie noch die Frage auf, ob ein frei fallendes Bezugssystem (lokal) in Newton's Sinne ein Inertialsystem wäre. |
Nein, das ist es üblicherweise nicht, aber man kann es als solches betrachten (und tut das häufig auch). Beispielsweise kann man das Schwerpunktsystem des Sonnensystems als Inertialsystem ansehen, obwohl es es sich im freien Fall um das Zentrum der Milchtraße befindet. Die laut Newton zwischen den Bestandteilen des Sonnensystems und dem Rest des Universums wirkenden Wechselwirkungskräfte werden dabei einfach vernachlässigt. |
|
 |
manuel459
Anmeldungsdatum: 11.10.2016
Beiträge: 263
|
 manuel459 Verfasst am: 04. März 2021 17:09 Titel: manuel459 Verfasst am: 04. März 2021 17:09 Titel: |
 |
|
Vielen Dank!
Okay damit greift man Argument aber nicht mehr "laut Einstein kein Inertialsystem weil stets die Bodenkraft wirkt". Wie könnte man dann argumentieren, dass dieses Ruhesystem des Zugs kein Inertialsystem ist? Weil kräftefreie Körper sich nicht gleichförmig geradlinig bewegen? Dann müsste aber der Minkowski Raum aber irgendwie vom Zug aus definiert werden oder?
Ist ein frei fallendes System dann deshalb kein Inertialsystem nach Newton weil die Gravitation auf einzelne Körper darin wirkt? Aus Sicht des Bezugssystems "weiß" man aber ja gar nichts von der Gravitation oder? |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 04. März 2021 17:31 Titel: DrStupid Verfasst am: 04. März 2021 17:31 Titel: |
 |
|
| manuel459 hat Folgendes geschrieben: | | Ist ein frei fallendes System dann deshalb kein Inertialsystem nach Newton weil die Gravitation auf einzelne Körper darin wirkt? |
Nein. Wie ich oben schon sagte, wird ein Inertialsysten nicht dadurch charakterisiert, dass darin keine Kräfte wirken. Dass frei fallende Bezugssysteme üblicherweise keine Inertialsysteme sind, erkennt man man an der Verletztung der Impulserhaltung.
Nehmen wir als Beispiel mal die ISS. Die bewegt sich im freien Fall um die Erde herum. Für die ISS selbst und alles, was sich darin abspielt, kann man das nicht-rotierende Ruhesystem ihres Masseschwerpunktes in guter Näherung als Inertialsystem betrachten. Für die Erde gilt das aber offensichtlich nicht mehr. Die bewegt sich in diesem Bezugssystem auf einer Kreisbahn um die ISS. Das verstößt gegen die Impulserhaltung.
Zuletzt bearbeitet von DrStupid am 04. März 2021 17:38, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 04. März 2021 17:36 Titel: TomS Verfasst am: 04. März 2021 17:36 Titel: |
 |
|
| manuel459 hat Folgendes geschrieben: | | Ist ein frei fallendes System dann deshalb kein Inertialsystem nach Newton weil die Gravitation auf einzelne Körper darin wirkt? |
Ein im Gravitationsfeld frei fallendes System S ist nach Newton deshalb kein Inertialsystem weil es nicht geradlinig gleichförmig fällt, sondern (bzgl. der Koordinaten im absoluten Raum) beschleunigt.
| manuel459 hat Folgendes geschrieben: | | Aus Sicht des Bezugssystems "weiß" man aber ja gar nichts von der Gravitation oder? |
Genau.
Der mit dem System S frei fallende Beobachter würde in einem geschlossenen Raum natürlich davon ausgehen, dass S ein Inertialsystem ist, da sich andere kräftefreie Körper ebenfalls geradlinig gleichförmig bewegen.
Nur von außen betrachtet - aus Sicht eines auf der Erde ruhenden und damit nicht kräftefreien Beobachters, oder aus Sicht um die Erde frei fallenden Satelliten - bewegt sich das frei fallende System S auf einer elliptischen Bahn und damit nicht geradlinig gleichförmig.
Wir haben also einen aus eigener Sicht kräftefrei fallenden Beobachter, der jedoch nach Newton deswegen beschleunigt fällt, weil er aufgrund der Gravitationskraft nicht kräftefrei ist. Das erscheint irgendwie widersinnig.
Die Definition der Inertialsysteme ist m.E. kein guter Ausgangspunkt, um die ART zu erklären. Erstens ist die Definition heikel, da sie leicht zirkulär wird. Und zweitens ist ein Inertialsystem ohnehin nur ein formales Gebilde; real sind Beobachter und gemessene Kräfte.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 04. März 2021 17:42 Titel: DrStupid Verfasst am: 04. März 2021 17:42 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Ein im Gravitationsfeld frei fallendes System S ist nach Newton deshalb kein Inertialsystem weil es nicht geradlinig gleichförmig fällt, sondern (bzgl. der Koordinaten im absoluten Raum) beschleunigt. |
Gehört es zur Definition eines Inertialsystems, dass es sich geradlinig-gleichförmig bewegt? Man kann zwar schlussfolgern, dass sich in der klassischen Mechanik zwei Inertialsysteme relativ zueinander geradlinig-gleichförmig bewegen müssen, aber explizit festgelegt wird das meines Wissens nicht.
Und selbst wenn man das so festlegt, bliebe dann immer noch die Frage, welches von zwei Bezuggsystemen, die relativ zueihnander beschleunigt sind, kein Inertialsystem ist. |
|
 |
manuel459
Anmeldungsdatum: 11.10.2016
Beiträge: 263
|
 manuel459 Verfasst am: 04. März 2021 17:43 Titel: manuel459 Verfasst am: 04. März 2021 17:43 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
Der mit dem System S frei fallende Beobachter würde in einem geschlossenen Raum natürlich davon ausgehen, dass S ein Inertialsystem ist, da sich andere kräftefreie Körper ebenfalls geradlinig gleichförmig bewegen.
Nur von außen betrachtet - aus Sicht eines auf der Erde ruhenden und damit nicht kräftefreien Beobachters, oder aus Sicht um die Erde frei fallenden Satelliten - bewegt sich das frei fallende System S auf einer elliptischen Bahn und damit nicht geradlinig gleichförmig.
|
Das macht für mich irgendwie gerade keinen Sinn. Es kann doch nicht vom "Blickwinkel" abhängen (also von der Menge an Information, die man besitzt), um etwas als Inertialsystem zu erkennen.  |
|
 |
manuel459
Anmeldungsdatum: 11.10.2016
Beiträge: 263
|
 manuel459 Verfasst am: 04. März 2021 17:45 Titel: manuel459 Verfasst am: 04. März 2021 17:45 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: |
Nein. Wie ich oben schon sagte, wird ein Inertialsysten nicht dadurch charakterisiert, dass darin keine Kräfte wirken. Dass frei fallende Bezugssysteme üblicherweise keine Inertialsysteme sind, erkennt man man an der Verletztung der Impulserhaltung.
|
und mit "üblicherweise" ist hier also die Newtonsche Sichtweise gemeint richtig? Okay das verstehe ich. Danke! |
|
 |
A.T.
Anmeldungsdatum: 06.02.2010
Beiträge: 343
|
 A.T. Verfasst am: 04. März 2021 18:07 Titel: A.T. Verfasst am: 04. März 2021 18:07 Titel: |
 |
|
| manuel459 hat Folgendes geschrieben: | | Ist ein frei fallendes System dann deshalb kein Inertialsystem nach Newton weil die Gravitation auf einzelne Körper darin wirkt? |
Nach Newton ist ein frei fallendes System kein Inertialsystem, weil Newton's Gesetze dort nicht gelten: Freifallende Körper haben keine Beschleunigung, obwohl die Newtonische Gravitation auf sie wirkt. Das verstößt gegen das 2-te Newtonische Gesetz. Du must Scheinkräfte einführen um die Beschleunigungen mit dem 2-tem Newtonische Gesetz konsistent zu machen, daher kein Inertialsystem.
Die ART lässt die Newtonische Gravitation weg, und braucht dann keine Scheinkräfte mehr um die lokalen Beschleunigungen im frei fallendem System zu erklären, daher lokal ein Inertialsystem. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 04. März 2021 18:20 Titel: DrStupid Verfasst am: 04. März 2021 18:20 Titel: |
 |
|
| manuel459 hat Folgendes geschrieben: | | und mit "üblicherweise" ist hier also die Newtonsche Sichtweise gemeint richtig? |
Nein, mit "üblicherweise" ist gemeint, dass es Ausnahmefälle gibt, in denen ein lokal frei fallendes Bezugssystem auch bei Newton ein echtes Inertialsystem ist - z.B. das Ruhesystem eines Sterns, der irgendwo einsam in einem Void herumdümpelt. In unserer Erfahrungswelt sind frei fallende Bezugssysteme aber keine klassischen Inertialsysteme, sondern bestenfalls lokal begrenzte Näherungen. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 04. März 2021 18:29 Titel: DrStupid Verfasst am: 04. März 2021 18:29 Titel: |
 |
|
| A.T. hat Folgendes geschrieben: | | Du must Scheinkräfte einführen um die Beschleunigungen mit dem 2-tem Newtonische Gesetz konsistent zu machen |
...oder Gravitationskräfte ignorieren. Newton hat das Sonnensystem als ruhend angenommen, weil er nichts von Galaxien und Galaxienhaufen wusste. Heute wissen wir es zwar besser, aber solange wir uns auf das Sonnensystem beschränken, können wir es genauso handhaben wie er, ohne Fehler zu machen, die irgendwie relevant wären. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 04. März 2021 18:29 Titel: index_razor Verfasst am: 04. März 2021 18:29 Titel: |
 |
|
| manuel459 hat Folgendes geschrieben: |
Ich versuche mich einmal an einer (von mir erstellten) Definition eines Inertialsystems - wäre toll wenn jemand seinen Senf dazugeben kann! 
Also ich definiere Inertialsysteme als Bezugssysteme, in denen der Trägheitssatz gilt. Dieser lautet "kräftefreie Körper bewegen sich geradlinig gleichförmig".
Hier wird aber nicht definiert, was "geradlinig gleichförmig" bedeutet, sondern man muss vorher schon wissen, was das bedeutet. Newton meint damit "Geraden" im Sinne der euklidischen Geometrie. Einstein meint Geodäten im Minkowski Raum).
|
Geradlinig-gleichförmige Bewegung ist sowohl in der Newtonschen Mechanik als auch in der ART unabhängig vom Bezugssystem definiert.
In der ART bedeutet es einfach, daß sich der Körper auf einer Geodäten bewegt, also in der Notation von TomS weiter oben
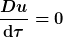
gilt. In der Newtonschen Mechanik bedeutet es fast dasselbe, nämlich, daß die Ableitung der Bahngeschwindigkeit nach der absoluten Zeit verschwindet
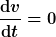 . .
Die Geschwindigkeit ist hier als Vektor im absoluten Raum aufzufassen, also als geometrisches, koordinatenunabhängiges Objekt.
Die Definition von Inertialsystem als System, in dem der Trägheitssatz gilt, ist also ohne Inhalt, da dann formal alle Systeme Inertialsysteme wären.
Ein Inertialsystem in der Newtonschen Mechanik kann definiert werden, als System dessen Ursprung geradlinig gleichförmig bzgl. des absoluten Raums bewegt ist und dessen Achsen sich im Raum nicht mit der absoluten Zeit ändern. Wenn man die Theorie ohne Bezug auf absolute Bewegung formulieren will, benötigt man eine 4dimensionale affine Newtonsche Raumzeit. (Siehe z.B. Arnold, Mathematical Methods of Classical Mechanics) Diese führt, genau wie die ART, den Begriff "geradlinig-gleichförmig" als Grundbegriff ein. In beiden Varianten haben Inertialsysteme die Eigenschaft, daß die Beschleunigung
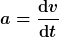
gleich der "Beschleunigung relativ zum gewählten Bezugssystem" ist. Die letztere Größe ist definiert als
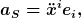
wobei 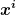 die Komponenten des Ortsvektor vom Ursprung aus sind. die Komponenten des Ortsvektor vom Ursprung aus sind.
Die Gleichheit 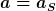 bedeutet wiederum, daß es keine Scheinkräfte gibt. bedeutet wiederum, daß es keine Scheinkräfte gibt.
In der ART ist die Definition von Inertialsystem ganz analog: der Ursprung bewegt sich auf einer Geodäten und die Koordinatenachsen werden drehungsfrei mitgeführt. (Letzteres kann man geometrisch durch das Verschwinden der Fermi-Walker-Ableitung definieren.) Wegen der Krümmung der Raumzeit liefert diese Definition aber im allgemeinen nur ein lokales Inertialsystem in dem Sinne, daß für einen kräftefreien Körper nur im Ursprung die Koordinatengleichung
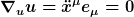
gilt.
| Zitat: |
Mir drängt sich nach diesem Text irgendwie noch die Frage auf, ob ein frei fallendes Bezugssystem (lokal) in Newton's Sinne ein Inertialsystem wäre.
|
Das hängt davon ab, wie man das Äquivalenzprinzip in die Newtonsche Theorie einbaut. Wenn man die frei fallende Bewegung eines Testteilchen als "geradlinig-gleichförmig" definiert, dann definieren Testteilchen lokale Inertialsysteme ugefähr auf die Art, die ich oben angegeben habe. Wenn nicht, dann definieren sie kein Inertialsystem, denn ein kräftefreies Teilchen, hat relativ zum Testteilchen die Beschleunigung
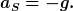
Zuletzt bearbeitet von index_razor am 04. März 2021 18:32, insgesamt 3-mal bearbeitet |
|
 |
Qubit
Anmeldungsdatum: 17.10.2019
Beiträge: 851
|
 Qubit Verfasst am: 04. März 2021 18:29 Titel: Re: Inertialsysteme Qubit Verfasst am: 04. März 2021 18:29 Titel: Re: Inertialsysteme |
 |
|
| manuel459 hat Folgendes geschrieben: |
ich habe Verständnisschwierigkeit wenn es um Inertialsysteme geht.
|
Der Begriff ist nicht ganz so einfach, wie er zuerst scheint.
Vielleicht interessieren dich dazu paar "historische" Anmerkungen?
https://www.pro-physik.de/restricted-files/85956 |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 04. März 2021 18:41 Titel: index_razor Verfasst am: 04. März 2021 18:41 Titel: |
 |
|
| A.T. hat Folgendes geschrieben: | | manuel459 hat Folgendes geschrieben: | | Ist ein frei fallendes System dann deshalb kein Inertialsystem nach Newton weil die Gravitation auf einzelne Körper darin wirkt? |
Nach Newton ist ein frei fallendes System kein Inertialsystem, weil Newton's Gesetze dort nicht gelten: |
Die Behauptung, daß Newtons Axiome nur in Inertialsystemen gelten, halte ich für eine verwirrende Fehlinformation, die leider schlecht auszurotten ist.
Ich habe zuletzt hier versucht, etwas Licht ins Dunkel zu bringen. Falls du dazu sachliche Anmerkungen hast, würden sie mich interessieren. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 04. März 2021 19:10 Titel: DrStupid Verfasst am: 04. März 2021 19:10 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Die Behauptung, daß Newtons Axiome nur in Inertialsystemen gelten, halte ich für eine verwirrende Fehlinformation, die leider schlecht auszurotten ist. |
Wie erkennst Du denn ein Nicht-Inertialsystem als solches, wenn nicht durch eine Verletzung der Newtonschen Axiome? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 04. März 2021 19:19 Titel: index_razor Verfasst am: 04. März 2021 19:19 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Die Behauptung, daß Newtons Axiome nur in Inertialsystemen gelten, halte ich für eine verwirrende Fehlinformation, die leider schlecht auszurotten ist. |
Wie erkennst Du denn ein Nicht-Inertialsystem als solches, wenn nicht durch eine Verletzung der Newtonschen Axiome? |
Den Begriff Inertialsystem habe ich weiter oben in meiner Antwort an manuel459 definiert. Die Frage ist übrigens gar nicht, wie ich Inertialsysteme erkenne, sondern wie ich die Newtonschen Axiome unabhängig vom Bezugssystem formuliere. Das dies geht, war nämlich der Inhalt meiner Behauptung. Inertialsysteme sind in der Hinsicht zweitrangig. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 04. März 2021 19:26 Titel: DrStupid Verfasst am: 04. März 2021 19:26 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Die Frage ist übrigens gar nicht, wie ich Inertialsysteme erkenne, sondern wie ich die Newtonschen Axiome unabhängig vom Bezugssystem formuliere. |
Doch, das ist die Frage und die Newtonschen Axiome sind eine Antwort. Wenn Du glaubst, dass es anders geht, dann raus damit. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 04. März 2021 19:38 Titel: index_razor Verfasst am: 04. März 2021 19:38 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Die Frage ist übrigens gar nicht, wie ich Inertialsysteme erkenne, sondern wie ich die Newtonschen Axiome unabhängig vom Bezugssystem formuliere. |
Doch, das ist die Frage und die Newtonschen Axiome sind eine Antwort. Wenn Du glaubst, dass es anders geht, dann raus damit. |
Die Antwort steht doch oben. Wenn du dazu eine konkrete Frage hast, dann raus damit. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 04. März 2021 19:42 Titel: DrStupid Verfasst am: 04. März 2021 19:42 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Die Antwort steht doch oben. |
Wo genau? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 04. März 2021 19:49 Titel: index_razor Verfasst am: 04. März 2021 19:49 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Die Antwort steht doch oben. |
Wo genau? |
In meiner Antwort an manuel459 steht eine Definition von Inertialsystem.
Es sollte einleuchten, daß es in einer bezuggsystemunabhängigen Formulierung der Newtonschen Axiome völlig unmöglich ist, Inertialsysteme daran zu erkennen, daß die Newtonschen Axiome in ihnen nicht gelten. Wie so eine bezuggsystemunabhängige Formulierung aussieht, weißt du. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 04. März 2021 20:00 Titel: DrStupid Verfasst am: 04. März 2021 20:00 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | In meiner Antwort an manuel459 steht eine Definition von Inertialsystem. |
Ja, das sehe ich. Was ich nicht sehe ist eine Antwort auf meine Frage, wie Du ein Nicht-Inertialsystem als solches erkennst. Möglicherweise übersehe ich das ja. In dem Fall könntest Du mir vielleicht weiterhelfen, indem Du an einem Beispiel erläuterst, wie man dabei vorgeht.
| index_razor hat Folgendes geschrieben: | | Es sollte einleuchten, daß es in einer bezuggsystemunabhängigen Formulierung der Newtonschen Axiome völlig unmöglich ist, Inertialsysteme daran zu erkennen, daß die Newtonschen Axiome in ihnen nicht gelten. |
Es sollte einleuchten, wie nutzlos das im Rahmen dieser Diskussion ist. Dass man die Newtonschen Axiome so formulieren kann, heißt nicht, dass man es so machen muss und wenn man es nicht tut, dann sind sie sehr gut für eine Definition von Inertialsystemen geeignet, die auch praktisch angewendet werden kann. Die Idee von manuel459 war also vollkommen richtig und Deine Reaktion darauf alles andere als hilfreich - es sei denn, Du kannst uns eine zumindest gleichwertige Alternative nennen. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 04. März 2021 20:28 Titel: TomS Verfasst am: 04. März 2021 20:28 Titel: |
 |
|
| manuel459 hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: |
Der mit dem System S frei fallende Beobachter würde in einem geschlossenen Raum natürlich davon ausgehen, dass S ein Inertialsystem ist, da sich andere kräftefreie Körper ebenfalls geradlinig gleichförmig bewegen.
Nur von außen betrachtet - aus Sicht eines auf der Erde ruhenden und damit nicht kräftefreien Beobachters, oder aus Sicht um die Erde frei fallenden Satelliten - bewegt sich das frei fallende System S auf einer elliptischen Bahn und damit nicht geradlinig gleichförmig.
|
Das macht für mich irgendwie gerade keinen Sinn. Es kann doch nicht vom "Blickwinkel" abhängen (also von der Menge an Information, die man besitzt), um etwas als Inertialsystem zu erkennen. ?( |
Definition: in einem Inertialsystem bewegt sich eine kräftefreie Masse geradlinig gleichförmig.
Frei fallender Aufzug, Innensicht: der Beobachter und der Testkörper sind kräftefrei; beide bewegen sich geradlinig gleichförmig.
Frei fallender Aufzug, Außensicht: der Beobachter und der Testkörper sind nicht kräftefrei, auf sie wirkt die Gravitationskraft; beide bewegen sich nicht geradlinig gleichförmig sondern beschleunigt.
Es ist auch keineswegs so, dass die Newtonsche Mechanik nur in Inertialsystemen gilt; die Bewegungsgleichungen nehmen lediglich eine besonders einfache Form an, da in nicht-Inertialsystemen zusätzlich Scheinkräfte auftreten.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 04. März 2021 20:49 Titel: DrStupid Verfasst am: 04. März 2021 20:49 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Es ist auch keineswegs so, dass die Newtonsche Mechanik nur in Inertialsystemen gilt; die Bewegungsgleichungen nehmen lediglich eine besonders einfache Form an, da in nicht-Inertialsystemen zusätzlich Scheinkräfte auftreten. |
Das kommt darauf an, wie eng man die Newtonsche Mechanik definiert. Selbst Newton war da offenbar etwas unschlüssig. In der ursprünglichen Formulierung seines dritten Axioms hat er Scheinkräfte ausgeschlossen. Später hat er sich dann aber entschieden: http://cudl.lib.cam.ac.uk/view/PR-ADV-B-00039-00001/49 |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 04. März 2021 20:53 Titel: index_razor Verfasst am: 04. März 2021 20:53 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | In meiner Antwort an manuel459 steht eine Definition von Inertialsystem. |
Ja, das sehe ich. Was ich nicht sehe ist eine Antwort auf meine Frage, wie Du ein Nicht-Inertialsystem als solches erkennst.
|
Ja, ich dachte mir schon, daß du das nicht "siehst". Antwort: man erkennt Inertialsysteme daran, daß sie die Definition von "Inertialsystem" erfüllen, die ich oben gegeben habe. Eine bessere Antwort hast du auch nicht, nur eine andere Definition.
| Zitat: |
Die Idee von manuel459 war also vollkommen richtig und Deine Reaktion darauf alles andere als hilfreich - es sei denn, Du kannst uns eine zumindest gleichwertige Alternative nennen. |
Daß beide Formulierungen völlig äquivalent sind, ist absolut trivial zu zeigen. Die Beziehung, die "nur in Inertialsystemen gilt", ist
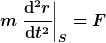 . .
Siehe den Link auf den anderen thread weiter oben. Da steht auch in welchem Zusammenhang sie zum 2. Newtonschen Axiom steht. Damit kannst du nun also deine eigene Antwort, wie auch immer sie lautet, problemlos auf meine Formulierung übertragen. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 04. März 2021 21:18 Titel: TomS Verfasst am: 04. März 2021 21:18 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Es ist auch keineswegs so, dass die Newtonsche Mechanik nur in Inertialsystemen gilt; die Bewegungsgleichungen nehmen lediglich eine besonders einfache Form an, da in nicht-Inertialsystemen zusätzlich Scheinkräfte auftreten. |
Das kommt darauf an, wie eng man die Newtonsche Mechanik definiert. Selbst Newton war da offenbar etwas unschlüssig. In der ursprünglichen Formulierung seines dritten Axioms hat er Scheinkräfte ausgeschlossen. Später hat er sich dann aber entschieden: http://cudl.lib.cam.ac.uk/view/PR-ADV-B-00039-00001/49 |
Ein einfaches Beispiel ist die Corioliskraft im rotierenden Bezugsystem; was wäre das, wenn nicht Newtonsche Mechanik?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 04. März 2021 21:54 Titel: DrStupid Verfasst am: 04. März 2021 21:54 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Antwort: man erkennt Inertialsysteme daran, daß sie die Definition von "Inertialsystem" erfüllen, die ich oben gegeben habe. |
Der Antwort auf meine Frage, wie man das erkennt, bist Du damit noch keinen Schritt näher gekommen.
| index_razor hat Folgendes geschrieben: | | Eine bessere Antwort hast du auch nicht, nur eine andere Definition. |
Ich habe oben geschrieben, wie man das mit Hilfe der Newtonschen Axiome anstellt: Man misst Impulse und prüft, ob ihre Summe konstant bleibt. Auf Deinen Gegenvorschlag warte ich bisher vergebens.
| index_razor hat Folgendes geschrieben: | | Damit kannst du nun also deine eigene Antwort, wie auch immer sie lautet, problemlos auf meine Formulierung übertragen. |
Warum sollte ich das für Dich tun? |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 04. März 2021 22:03 Titel: DrStupid Verfasst am: 04. März 2021 22:03 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Ein einfaches Beispiel ist die Corioliskraft im rotierenden Bezugsystem; was wäre das, wenn nicht Newtonsche Mechanik? |
Da Zentrifugal- und Corioliskräfte nicht paarweise auftreten, sind sie nach der ursprünglichen Formulierung des dritten Axioms keine Kräfte. Im Inertialsystem kräftefreie Körper sind damit auch im rotierenden System kräftefrei. Da sie sich dort aber nicht notwendigerweise geradlinig-gleichförmig bewegen, liegt hier ein Verstoß gegen das erste Axiom vor. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 04. März 2021 22:20 Titel: index_razor Verfasst am: 04. März 2021 22:20 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Antwort: man erkennt Inertialsysteme daran, daß sie die Definition von "Inertialsystem" erfüllen, die ich oben gegeben habe. |
Der Antwort auf meine Frage, wie man das erkennt, bist Du damit noch keinen Schritt näher gekommen.
|
So nahe, wie es bei einer so allgemeinen Frage eben möglich ist.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Eine bessere Antwort hast du auch nicht, nur eine andere Definition. |
Ich habe oben geschrieben, wie man das mit Hilfe der Newtonschen Axiome anstellt: Man misst Impulse und prüft, ob ihre Summe konstant bleibt. Auf Deinen Gegenvorschlag warte ich bisher vergebens.
|
Man prüft die Gültigkeit der Beziehung 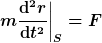 . Das ist die direkte Antwort auf deine Frage: "Wie erkennst Du denn ein Nicht-Inertialsystem als solches, wenn nicht durch eine Verletzung der Newtonschen Axiome?" Ich könnte dir das noch hundertmal erklären, du würdest trotzdem nichts verstehen und behaupten noch immer auf meine Erklärung zu warten. Aus der Erfahrung kann ich leider nichts anderes schließen. . Das ist die direkte Antwort auf deine Frage: "Wie erkennst Du denn ein Nicht-Inertialsystem als solches, wenn nicht durch eine Verletzung der Newtonschen Axiome?" Ich könnte dir das noch hundertmal erklären, du würdest trotzdem nichts verstehen und behaupten noch immer auf meine Erklärung zu warten. Aus der Erfahrung kann ich leider nichts anderes schließen.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Damit kannst du nun also deine eigene Antwort, wie auch immer sie lautet, problemlos auf meine Formulierung übertragen. |
Warum sollte ich das für Dich tun? |
Weil du mich immer wieder dasselbe fragst (nicht nur in dieser Diskussion) und meine Antworten dir offenbar nicht helfen. Und ein bißchen Eigeninitiative wird hier jedem gern empfohlen, der etwas dazulernen will. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 04. März 2021 23:02 Titel: DrStupid Verfasst am: 04. März 2021 23:02 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | Man prüft die Gültigkeit der Beziehung 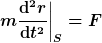 . . |
Wie bestimmt man F? |
|
 |
A.T.
Anmeldungsdatum: 06.02.2010
Beiträge: 343
|
 A.T. Verfasst am: 05. März 2021 07:15 Titel: A.T. Verfasst am: 05. März 2021 07:15 Titel: |
 |
|
| A.T. hat Folgendes geschrieben: | | manuel459 hat Folgendes geschrieben: | | Ist ein frei fallendes System dann deshalb kein Inertialsystem nach Newton weil die Gravitation auf einzelne Körper darin wirkt? |
Nach Newton ist ein frei fallendes System kein Inertialsystem, weil Newton's Gesetze dort nicht gelten: Freifallende Körper haben keine Beschleunigung, obwohl die Newtonische Gravitation auf sie wirkt. Das verstößt gegen das 2-te Newtonische Gesetz. Du must Scheinkräfte einführen um die Beschleunigungen mit dem 2-tem Newtonische Gesetz konsistent zu machen, daher kein Inertialsystem. |
Eigentlich sollte klar sein, dass hier mit "Newtons Gesetze" die ursprüngliche Formulierung, ohne Scheinkräfte gemeint ist, weil die Scheinkräfte explizit das nicht inertiale System differenzieren sollen.
Zuletzt bearbeitet von A.T. am 05. März 2021 07:23, insgesamt einmal bearbeitet |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 05. März 2021 07:20 Titel: index_razor Verfasst am: 05. März 2021 07:20 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | Man prüft die Gültigkeit der Beziehung 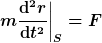 . . |
Wie bestimmt man F? |
Wie du willst. Direkt erforderlich ist das ja anscheinend nicht. Schließlich geht es ja auch so: "Man misst Impulse und prüft, ob ihre Summe konstant bleibt." Das kann ich genauso tun. Ich muß dazu nur exakt dieselbe Definition von Impulsänderung verwenden wie du. (Ich vermute mal da wird es ein paar Unterschiede geben, die vermutlich auch, aber nicht nur auf dem Unterschied zwischen
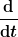 und und 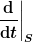
beruhen.) Das widerspricht aber selbstverständlich nicht meiner Voraussetzung, daß die Newtonschen Axiome unabhängig vom Bezugssystem gelten. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 05. März 2021 07:23 Titel: index_razor Verfasst am: 05. März 2021 07:23 Titel: |
 |
|
| A.T. hat Folgendes geschrieben: | | A.T. hat Folgendes geschrieben: | | manuel459 hat Folgendes geschrieben: | | Ist ein frei fallendes System dann deshalb kein Inertialsystem nach Newton weil die Gravitation auf einzelne Körper darin wirkt? |
Nach Newton ist ein frei fallendes System kein Inertialsystem, weil Newton's Gesetze dort nicht gelten: Freifallende Körper haben keine Beschleunigung, obwohl die Newtonische Gravitation auf sie wirkt. Das verstößt gegen das 2-te Newtonische Gesetz. Du must Scheinkräfte einführen um die Beschleunigungen mit dem 2-tem Newtonische Gesetz konsistent zu machen, daher kein Inertialsystem. |
Eigentlich sollte klar sein das hier mit "Newton's Gesetze" die ursprüngliche Formulierung, ohne Scheinkräfte gemeint ist, weil die Scheinkräfte das nicht inertiale System differenzieren sollen. |
Die Formulierung ohne Scheinkräfte ist vollkommen äquivalent zur Formulierung mit Scheinkräften. Zu beiden Formulierungen nicht äquivalent ist z.B. die Gleichung
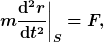
die nur in Inertialsystemen gilt, aber auch oft als "2. Newtonsches Axiom" bezeichnet wird. |
|
 |
A.T.
Anmeldungsdatum: 06.02.2010
Beiträge: 343
|
 A.T. Verfasst am: 05. März 2021 07:38 Titel: A.T. Verfasst am: 05. März 2021 07:38 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: |
... die nur in Inertialsystemen gilt, aber auch oft als "2. Newtonsches Axiom" bezeichnet wird. |
Ja, super. Dann nicht die Newtonschen Axiome, sondern das was als Newtonsche Axiome bezeichnet wird. Ich bin sicher diese Klarstellung hat dem OP total geholfen. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 05. März 2021 07:55 Titel: index_razor Verfasst am: 05. März 2021 07:55 Titel: |
 |
|
| A.T. hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: |
... die nur in Inertialsystemen gilt, aber auch oft als "2. Newtonsches Axiom" bezeichnet wird. |
Ja, super. Dann nicht die Newtonschen Axiome, sondern das was als Newtonsche Axiome bezeichnet wird. Ich bin sicher diese Klarstellung hat dem OP total geholfen. |
Die Antwort ging an dich, nicht an OP. Hilfreich ist es m.E. den Unterschied zwischen
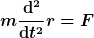
und
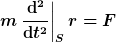
zu begreifen, der anscheinend auch dir nicht ganz geläufig ist.
Beide Gleichungen werden explizit oder implizit als 2. Newtonsches Axiom bezeichnet. Dein Sarkasmus ist also unangebracht. |
|
 |
|

















