FAQ - Newtonsche Mechanik, Inertialsysteme, Galileiinvarianz

TomS · Moderator Anmeldungsdatum: 20.03.2009 Beiträge: 18079

Aus gegebenen Anlass eine geometrische Darstellung der Newtonschen Mechanik, insbs. zur Klärung der Rolle von Koordinaten- und Inertialsystemen sowie der Rolle der Galileiinvarianz.

Ziel ist zunächst ein geometrischer Rahmen, innerhalb dessen die Newtonschen Gesetze formuliert sowie physikalische Systeme und deren Dynamik diskutiert werden können. Es soll gezeigt werden, wie Inertialsysteme aus der Symmetrie der Galileischen Raumzeit A folgen und dass ihre Definition nichts mit den später zu diskutierenden konkreten Körpern, Systemen und Kräften zu tun hat.

Ausgangspunkt ist ein Modell basierend auf einem 4-dim. Galileischen Raum (A,V,t).

A ist ein affiner Raum über einem reellen 4-dim. Vektorraum V mit Raumzeitpunkten als Elementen von A.

ist eine Zeitabstandsfunktion auf V. Zwei Raumzeitpunkte p,q aus A sind gleichzeitig, wenn

Daraus folgt die Untermenge aller zu p absolut gleichzeitigen Raumzeitpunkten als Äquivalenzklasse

Außerdem existiert eine (absolute) Abstandsfunktion

je Untermenge [p], die durch ein positive definites Skalarprodukt auf dem 3-dim. euklidischen, afffinen Unterraum induziert wird.

Auf diesem Galileischen Raum kann man natürlich entsprechende Koordinaten einführen. Ein Koordinatensystem f ist eine Abbildung

mit Koordinaten

Die Gruppe der Automorphismen Aut(G) auf dem zugehörigen Galileischen Koordinatenraum, die Galilei-Gruppe, enthält Raum- und Zeittranslationen, Rotationen und Boosts (Bewegungen):

Die oben eingeführte Struktur inkl. der Funktionen t, d ist invariant unter Aut(G).

Zwei Koordinatensysteme f, g sind zueinander relativ gleichförmig bewegt, wenn für die Verknüpfung

gilt.

Eine Galileische Struktur [f] entspricht einer Äquivalenzklasse von Galileischen Koordinatensystemen. Jedes derartige Koordinatensystem f liefert ein Inertialsystem; zwei Inertialsysteme f ~ g derselbe Galileischen Struktur [f] sind relativ zueinander gleichförmig bewegt; kein Inertialsystem ist ausgezeichnet, da wir keine Struktur eingeführt haben, das eine Auszeichnung liefern könnte.

Das Galileischen Relativitätsprinzip besagt nun, dass alle Naturgesetze in allen Inertialsystemen die selbe Form annehmen.

Das bedeutet nicht, dass nicht-Inertialsysteme in der Newtonschen Mechanik unzulässig wären, sondern lediglich, dass Naturgetze in diesen nicht unbedingt die selbe Form annehmen; d.h. die Gesetze der Newtonschen Mechanik können sehr wohl in nicht-Inertialsystemen formuliert werden. Ein Beispiel ist das mit konstanter Winkelgeschwindigkeit und konstanter Achse rotierende und damit zeitabhängige Koordinatensystem, das aus einer zeitabhängigen Rotation mittels

hervorgeht. Man beachte, dass

Damit ist die geometrische Bühne bereitet, um die Newtonschen Postulate geeignet zu formalisieren sowie konkrete physikalische Systeme und deren Dynamik einzuführen. Es ist klar, dass und wie Inertialsysteme aus der Symmetrie der Galileischen Raumzeit A folgen - und dass die Definition der Inertialsysteme nichts mit konkreten physikalischen Systemen, Körpern und Kräften zu tun hat, die wir noch gar nicht eingeführt haben. Es wird auch klar werden, dass physikalische Systeme auf A definiert werden, nicht auf G, und dass diese physikalischen Systeme damit unabhängig von Koordinatensystemen f sowie insbs. von Inertialsystemen sind. Am Beispiel des rotierenden Koordinatensystems: natürlich gelten für ein System, in dem Energie- und Impulserhaltung vorliegen, diese Erhaltungssätze auch bei Verwendung des rotierenden Koordinatensystems; dieses bricht selbstverständlich keine Symmetrie des Systems selbst.

TomS · Moderator Anmeldungsdatum: 20.03.2009 Beiträge: 18079

Der Vorteil der bisherigen formalen Darstellung ist, dass der geometrische Rahmen definiert wird, ohne zugleich Begriffe wie „Bezugsystem im Sinne eines Körpers, auf den sich etwas bezieht“, „Bewegung“, „Kraft“ o.ä. einzuführen. Die vermeintliche zirkuläre Definition von „Inertialsystem“ und „kräftefreier Bewegung“ wird vermieden.

Nun definiert man eine Trajektorie x(t) sowie den Graph der Trajektorie = die Weltlinie eines Körpers als

Geschwindigkeit und Beschleunigung folgen als erste und zweite Ableitung von x(t).

Betrachtet man ein System von N Körpern, so definiert man die Kraft F als eine Abbildung

mit

wobei rechts implizit die Gesamtheit aller N Orte und Geschwindigkeiten gemeint ist.

Die Newtonsche Bewegungsgleichung für ein System von i = 1..N Körpern, zwischen denen Kräfte F_i wirken, lautet

Bei gegebenen Anfangsbedingungen für Orte und Geschwindigkeiten folgen die Trajektorien des Systems eindeutig als Lösung dieser Bewegungsgleichung.

Man beachte, dass diese Bewegungsgleichung ohne Verwendung des Begriffs des Inertialsystems formuliert ist.

Der nächste Schritt ist die präzise Formulierung des Galileischen Relativitätsprinzips sowie die vollständige Darstellung der Newtonschen Gesetze, bzw. deren Einbettung in den o.g. formalen Rahmen.

1. Ein kräftefreier Körper ist in Ruhe oder bewegt sich geradlinig mit konstanter Geschwindigkeit.
2. Die zeitliche Änderung des Impulses eines Körpers entspricht der auf den Körper wirkenden Kraft.
3. Zwei Körper üben aufeinander betragsmäßig gleiche, entgegengesetzt gerichtete Kräfte aus.

Dabei muss zunächst betont werden, dass das o.g. Relativitätsprinzip

0. Alle Naturgesetze nehmen in allen Inertialsystemen die selbe Form an.

vereinbart werden muss mit dem 2. Newtonschen Gesetz, das in der o.g. Formulierung überhaupt keinen Bezug auf Inertialsysteme aufweist. Daher wird das Galileische Relativitätsprinzip neu formuliert werden müssen.

TomS · Moderator Anmeldungsdatum: 20.03.2009 Beiträge: 18079

Im Folgenden soll die Newtonsche Mechanik aus zwei Prinzipien entwickelt werden, dem Galileischen Relativitätsprinzip sowie dem zweiten Newtonschen Gesetz. Letzteres wurde oben bereits eingeführt, muss jedoch aufgrund des Relativitätsprinzips noch eingeschränkt werden.

Das Galileische Relativitätsprinzip kann man im wesentlichen wie folgt formulieren: Die physikalischen Gesetze, Systeme und Lösungen der Newtonschen Mechanik sind invariant unter den o.g. Galilei-Transformationen.

D.h. zunächst trägt der o.g. Galileische Koordinatenraum die Galilei-Gruppe als Symmetriegruppe. Damit können alle Gesetze so formuliert werden, dass insbs. keine Abhängigkeiten von Koordinatensystemen existieren, da sämtliche relevante physikalischen Entitäten wie physikalische Systeme, Kräfte und Trajektorien mit Äquivalenzklassen bzgl. der Galilei-Transformationen assoziiert werden können.

Insbs. folgt aus den beiden Voraussetzungen
i) dass das betrachtete System die geforderte Galilei-Invarianz nicht bricht, und
ii) dass eine Trajektorien x(t) das zweite Newtonsche Gesetz erfüllt,
dass eine beliebige Galilei-Transformation diese Lösung x(t) auf eine äquivalente Lösung y(t) des selben Systems abbildet; d.h. x(t) und y(t) können physikalisch identifiziert werden.

Mathematisch kann das Galileische Relativitätsprinzip wie folgt formuliert werden: Gegeben sei ein Galileischer Raum A, Inertialsysteme f, ein Eigenzeitintervall I sowie der Graph einer Trajektorie

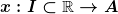
x(t) ist eine zulässige Trajektorie, wenn für alle Inertialsysteme

die Abbildung

der Graph einer Trajektorie ist, die die Newtonsche Bewegungsgleichung erfüllt.

Damit die Kraft in diesem Sinne zulässige Bewegungen erzeugt, muss sie folgende Eigenschaften aufweisen:
- sie hängt nicht explizit von der Zeit ab
- sie hängt nur von den Relativkoordinaten der Körper ab
- sie hängt nur von den Relativgeschwindigkeiten der Körper ab
- sie transformiert als Vektor unter Rotationen
Dies entspricht gerade der Symmetrie unter den Erzeugenden der Galilei-Gruppe: Zeit- sowie Raum-Translationen, Boosts, Rotationen.

Aus diesen einschränkenden Bedingungen folgen die zulässigen Kräfte sowie die mit dem Galileischen Relativitätsprinzip verträgliche Form des zweiten Newtonschen Gesetzes bzw. die Newtonsche Bewegungsgleichung

Außerdem folgen sofort das erste und das dritte Newtonsche Gesetz.

Seien g Galilei-Transformationen (ohne Zeit-Translationen) und sei x(t) eine Trajektorie, die eine Newtonsche Bewegungsgleichung mit bzgl. der Galilei-Symmetrie zulässiger Kraft F löst. Dann erzeugen die Transformationen

äquivalente Kräfte und Trajektorien, d.h. Äquivalenzklassen

bzgl. der Gruppe der Galilei-Transformationen.

Eine physikalische Kraft sowie die resultierende physikalische Trajektorie entsprechen den Äquivalenzklassen [F] bzw. [x].

Zusammenfassung: Aus dem Galileischen Relativitätsprinzip folgen einschränkende Bedingungen für die in der Newtonschen Bewegungsgleichung zulässigen Kräfte. Sind diese Bedingungen erfüllt, so überführt jede Galilei-Transformation eine Lösung x(t) der Newtonschen Bewegungsgleichung in eine äquivalente Lösung y(t). Beide Lösungen beschreiben die selbe physikalische Bewegung, betrachtet in einem anderen Inertialsystem.

Anmerkung 1: Dennoch können auch andere Koordinatensysteme zur Formulierung der Newtonschen Mechanik und der Newtonschen Bewegungsgleichung verwendet werden. Voraussetzung ist jedoch, dass die auftretende Kraft F - wenn sie in einem Inertialsystem betrachtet wird - die o.g. einschränkenden Bedingungen erfüllt. D.h. die Inertialsysteme sind ausschließlich dadurch ausgezeichnet, als sie zur Charakterisierung der zulässigen Kräfte dienen.

Anmerkung 2: Bisher haben wir die Inertialsysteme noch nicht mit realen Beobachtern assoziiert. Auch hier ist es durchaus möglich, nicht-inertiale Beobachter zu betrachten.

Anmerkung 3: In der Praxis werden häufig Systeme mit externen Kräften diskutiert, die die Galilei-Invarianz explizit brechen (z.B. der Fall eines Körpers im Gravitationsfeld mit Feldstärke = Ortsfaktor g oder die Bewegung eines Körpers in einem Medium einschließlich Reibung). In allen Fällen kann von einem zugrundeliegenden System ausgegangen werden, das die Galilei-Invarianz im o.g. Sinne respektiert (wobei die beiden genannten Beispiele als Näherung folgen: Vernachlässigung der Erde im Grenzfall Erdmasse gegen Unendlich; Modellierung der Flüssigkeit als externen Medium anstelle der Stöße mit einzelnen Molekülen).