| Autor |
Nachricht |
Voltobal
Gast
|
 Voltobal Verfasst am: 15. Aug 2020 00:04 Titel: Zeitentwicklung Maxwellgleichungen |
 |
|
Meine Frage:
Hi,
Ich sitze vor einem Problem der Elektrodynamik. Und zwar verstehe ich die Angabe einer Aufgabe nicht ganz. Sie lautet wie folgt:
"Die beiden Maxwellgleichungen
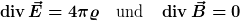
enthalten keine Zeitableitung und sind daher Bedingungen für die Anfangswerte der Felder. Zeige, dass sie durch die restlichen beiden "Zeitentwicklungsgleichungen" propagiert werden, d.h. immer gelten, wenn sie zu einer Zeit gelten."
Meine Ideen:
Nun ich denke, dass ich die Grundlagen der Elektrodynamik zwar halbwegs passabel beherrsche, nur habe ich hier das Problem, dass ich die Frage schon nicht so recht verstehe bzw. nicht ganz weiß was überhaupt zu tun ist. Kann mir jemand einen Tipp geben? Ich würde aber gerne selbst versuchen die Aufgabe zu lösen, ich bitte daher nur um einen Ansatz ;)
MfG
Voltobal |
|
 |
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18078
|
| TomS Verfasst am: 15. Aug 2020 07:05 Titel: |
|
|
Zum Hintergrund
Die erste der genannten Gleichungen spielt formal die Rolle einer Zwangsbedingung. Man kann die Lagrangedichte der Elektrodynamik so umformen, dass A° als Lagrangemultiplikator wirkt, so dass aus
genau diese Zwangsbedingung folgt. A° hat keinen konjugierten Impuls, daher ist A° kein dynamischer Freiheitsgrad.
Beide Gleichungen enthalten keine Zeitableitungen und erscheinen zunächst als Anfangsbedingung; das ist jedoch nur die halbe Wahrheit, denn aufgrund der zuvor genannten Argumentation müssen sie für alle Zeiten erfüllt sein. Das ist für eine gewöhnliche Anfangsbedingung nicht der Fall.
Man hat zwei Möglichkeiten, damit umzugehen:
1) Man löst die Gleichungen zu Beginn explizit. Bei der ersten Gleichung ist das nicht ganz einfach, da ein Differentialoperator zu invertieren ist. Bei der zweiten Gleichung erfolgt dies durch die Einführung des Vektorpotentials
Dies stellt automatisch sicher, dass die zweite Gleichung für alle Zeiten erfüllt ist.
2) Man löst die Gleichungen noch nicht, stellt jedoch sicher, dass die Zeitentwicklung sie respektiert. Das ist in der vorliegenden Aufgabe gefordert.
Zur Aufgabe
Am Beispiel der ersten Gleichung: es ist mittels der bekannten Gleichungen der Elektrodynamik zu zeigen, dass
 = 0)
identisch gilt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Voltobal
Gast
|
| Voltobal Verfasst am: 15. Aug 2020 11:20 Titel: |
|
|
Danke für die Antwort. Ich verstehe allerdings die Angabe bzw. die Aufgabe leider immer nicht ganz. Dass die Gleichung
 = 0 )
gilt, ist doch sowieso klar, oder nicht? Indem nämlich
 = 0 )
erfüllt ist, muss die Ableitung natürlich auch null sein.
MfG
Voltobal |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18078
|
| TomS Verfasst am: 15. Aug 2020 12:44 Titel: |
|
|
Genau das sollst du zeigen.
Sei
 - \tilde{\rho}(x,t) = 0)
und sei
 = \partial_x^{-1} \tilde{\rho}(x,t))
eine explizite Lösung E(x,t) für gegebene rechte Seite, z.B. mittels Fouriertransformation.
Sei außerdem
 = \tilde{\rho}(x,t) + \rho_0(t))
mit
 = 0)
Dann ist
 = \tilde{\rho}(x,t=0))
 - \rho(x,t=0) = 0)
ebenfalls eine Lösung für t=0, jedoch nicht für t>0, denn
 - \rho(x,t) = \partial_x E(x,t) - [\tilde{\rho}(x,t) + \rho_0(t)] = - \rho_0(t))
Wenn die Gleichung also als Anfangsbedingung interpretiert wird, dann garantiert die Lösung für alle x und ein t=0 nicht automatisch, dass die Gleichung auch für t>0 gelöst wird.
Du musst also die Zeitableitungen auf E und rho wirken lassen und mittels weiterer Gleichungen der Elektrodynamik explizit zeigen, dass die gegebene Gleichung damit automatisch erfüllt wird.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Voltobal
Gast
|
| Voltobal Verfasst am: 15. Aug 2020 18:20 Titel: |
|
|
Mein Ansatz dazu:
 \enspace = \enspace \operatorname{div} \partial_t \vec{E} - 4\pi \partial_t \varrho \\
<br />
<br />
= \enspace \operatorname{div} \big( \operatorname{rot} \vec{B} - 4\pi \vec{j} \big) - 4\pi \partial_t \varrho \\
<br />
<br />
= \enspace \underbrace{ \operatorname{div} \operatorname{rot} \vec{B}}_{= 0} - 4\pi \operatorname{div} \vec{j} - 4\pi \partial_t \varrho \\
<br />
<br />
= \enspace - 4\pi( \operatorname{div} \vec{j} + \partial_t \varrho \big)
<br />
<br />
)
Dies ist die Kontinuitätsgleichung und diese ist für alle Zeiten gleich Null. Ist die Lösung der Aufgabe derart gemeint?
MfG
Voltobal |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18078
|
| TomS Verfasst am: 15. Aug 2020 22:10 Titel: |
|
|
Genau, so ist das gemeint.
Die Maxwell-Gleichungen sind nur dann konsistent, wenn auch der Strom erhalten ist.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
|
|
Registrieren
Login
FAQ
Suchen
