| Autor |
Nachricht |
Physiker1.1
Anmeldungsdatum: 14.11.2021
Beiträge: 19
|
 Physiker1.1 Verfasst am: 17. Jan 2022 15:23 Titel: Dichtematrix - Zeitentwicklung Physiker1.1 Verfasst am: 17. Jan 2022 15:23 Titel: Dichtematrix - Zeitentwicklung |
 |
|
Meine Frage:
Hallo,
ich habe in dieser Aufgabe Folgendes gegeben:
Einen Hamiltonian des betrachteten quantenmechanischen Systems:

geschrieben in der Basis
 . .
Dabei sind die Zustände durch die (nicht entarteten) Eigenwerte eines
eines Operators A gekennzeichnet.
Zur Zeit t=0 ist die Dichtematrix als

gegeben.
Man soll nun die Wahrscheinlichkeit
)
dafür berechnen, dass man a_1 als Ergebnis bekommt, wenn man A zu einem späteren Zeitpunkt t misst.
Meine Ideen:
Ich habe versucht mit der Zeitentwicklung der Dichtematrix zu rechnen, also mit
 = U^{-1}(t)\rho_0U(t))
wobei U der Zeitentwicklungsoperator mit
 ist. ist.
Damit bin ich allerdings nicht weitergekommen. Ich bin mir nicht mal sicher, ob ich U in diesem Fall so darstellen darf, weil mein Hamiltonian ja eigentlich zeitabhängig ist, wenn ich die Zustände zeitentwickle, oder?
Kann mir jemand helfen? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
 TomS Verfasst am: 17. Jan 2022 16:21 Titel: TomS Verfasst am: 17. Jan 2022 16:21 Titel: |
 |
|
Nein, der Ansatz ist bis auf eine Kleinigkeit völlig korrekt.
Eines in einer bestimmten Basis diagonalen Dichteoperators lautet

wobei die Projektoren für t = 0 gegeben sind durch

Und mit der Zeitentwicklung der Zustände gemäß
 = \exp\left[-iHt\right])
\right\rangle = U(t) \, \left|a\right\rangle)
folgt die Zeitentwicklung des Dichteoperators gemäß der von-Neumann-Gleichung
 = U(t) \, \rho_0 \, U^\dagger(t) = \sum_a p_a \, U(t) \, E_a \, U^\dagger(t) )
Du hast 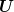 und und  vertauscht. So würde das für die Heisenberg-Gleichung als Bewegungsgleichung eines Operators im Heisenbergbild gelten; wir reden hier jedoch von der Zeitentwicklung eines Dichteoperators im Schrödingerbild, der den Zustand des Systems beschreibt. vertauscht. So würde das für die Heisenberg-Gleichung als Bewegungsgleichung eines Operators im Heisenbergbild gelten; wir reden hier jedoch von der Zeitentwicklung eines Dichteoperators im Schrödingerbild, der den Zustand des Systems beschreibt.
Dein Hamiltonian ist außerdem nicht zeitabhängig. Er lautet schlicht
)
bzw. in Matrixschreibweise unter Verwendung der Pauli-Matrix

Die Definition erfolgt mittels der Basisvektoren für t=0.
Mit der sehr nützlichen Identität - darfst du zur Übung gerne beweisen -
\right] = \cos a + i\left(\hat{n}\vec{\sigma}\right) \sin a )
kannst du deinen Zeitentwicklungsoperator ) explizit ausrechnen. Der Rest ist dann triviale Algebra. explizit ausrechnen. Der Rest ist dann triviale Algebra.
 ) steht für das Skalarprodukt aus einem beliebigen Einheitsvektor und dem Vektor der Paulimatrizen. In deinem Fall gilt steht für das Skalarprodukt aus einem beliebigen Einheitsvektor und dem Vektor der Paulimatrizen. In deinem Fall gilt
)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 17. Jan 2022 16:26, insgesamt einmal bearbeitet |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 17. Jan 2022 16:26 Titel: Re: Dichtematrix - Zeitentwicklung index_razor Verfasst am: 17. Jan 2022 16:26 Titel: Re: Dichtematrix - Zeitentwicklung |
 |
|
| Physiker1.1 hat Folgendes geschrieben: |
Meine Ideen:
Ich habe versucht mit der Zeitentwicklung der Dichtematrix zu rechnen, also mit
 = U^{-1}(t)\rho_0U(t))
wobei U der Zeitentwicklungsoperator mit
 ist. ist.
Damit bin ich allerdings nicht weitergekommen. Ich bin mir nicht mal sicher, ob ich U in diesem Fall so darstellen darf, weil mein Hamiltonian ja eigentlich zeitabhängig ist, wenn ich die Zustände zeitentwickle, oder?
|
Nein, H ist nicht zeitabhängig. Die Darstellung  = e^{-iHt}) ist also zulässig. Am einfachsten ist es wohl, wenn du H erstmal diagonalisierst und ist also zulässig. Am einfachsten ist es wohl, wenn du H erstmal diagonalisierst und 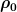 in der Energieeigenbasis darstellst. in der Energieeigenbasis darstellst. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
 TomS Verfasst am: 17. Jan 2022 16:29 Titel: Re: Dichtematrix - Zeitentwicklung TomS Verfasst am: 17. Jan 2022 16:29 Titel: Re: Dichtematrix - Zeitentwicklung |
 |
|
| index_razor hat Folgendes geschrieben: | Am einfachsten ist es wohl, wenn du H erstmal diagonalisierst und 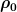 in der Energieeigenbasis darstellst. in der Energieeigenbasis darstellst. |
Würde ich nicht machen - s.o. - ist aber letztlich Geschmacksache.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 17. Jan 2022 16:51 Titel: Re: Dichtematrix - Zeitentwicklung index_razor Verfasst am: 17. Jan 2022 16:51 Titel: Re: Dichtematrix - Zeitentwicklung |
 |
|
| TomS hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | Am einfachsten ist es wohl, wenn du H erstmal diagonalisierst und 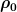 in der Energieeigenbasis darstellst. in der Energieeigenbasis darstellst. |
Würde ich nicht machen - s.o. - ist aber letztlich Geschmacksache. |
Kommt vielleicht darauf an, wie man es macht. In welcher Basis H diagonal ist, sieht man fast ohne Nachdenken.
Falls ich mich nicht verrechnet habe, ist
 = e^{i\omega t}|e_1\rangle\langle e_1| + e^{-i\omega t}|e_2\rangle\langle e_2|)
und
)
Damit kann man ) ja recht leicht ausrechnen. ja recht leicht ausrechnen. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 17. Jan 2022 18:17 Titel: index_razor Verfasst am: 17. Jan 2022 18:17 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
Mit der sehr nützlichen Identität - darfst du zur Übung gerne beweisen -
\right] = \cos a + i\left(\hat{n}\vec{\sigma}\right) \sin a )
kannst du deinen Zeitentwicklungsoperator ) explizit ausrechnen. explizit ausrechnen. |
Übrigens, für den Fragesteller ist vielleicht auch interessant, daß man diese Identität im vorliegenden Fall auch leicht direkt, ohne Umweg über die Pauli-Matrizen zeigen kann.
Mit ) (ich spare mir mal die Diracschreibweise, links stehen immer Kets, rechts Bras), kann man ja leicht sehen, daß für gerade Potenzen von (ich spare mir mal die Diracschreibweise, links stehen immer Kets, rechts Bras), kann man ja leicht sehen, daß für gerade Potenzen von  gilt gilt
^{2n} = (-1)^n (\omega t)^{2n}(a_1 a_1 + a_2a_2) = (-1)^n (\omega t)^{2n}.)
Der letzte Schritt gilt, weil  vollständig ist. Für ungerade Potenzen gilt vollständig ist. Für ungerade Potenzen gilt
^{2n+1} = -i (-1)^{n}(\omega t)^{2n+1}(a_1 a_2 + a_2a_1) )
Damit folgt auch über die Taylorreihen von Kosinus und Sinus
 = \cos(\omega t) - i\sin(\omega t)(a_1 a_2 + a_2 a_1).) |
|
 |
Physiker1.1
Anmeldungsdatum: 14.11.2021
Beiträge: 19
|
 Physiker1.1 Verfasst am: 17. Jan 2022 19:05 Titel: Physiker1.1 Verfasst am: 17. Jan 2022 19:05 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Nein, der Ansatz ist bis auf eine Kleinigkeit völlig korrekt.
Du hast 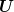 und und  vertauscht. So würde das für die Heisenberg-Gleichung als Bewegungsgleichung eines Operators im Heisenbergbild gelten; wir reden hier jedoch von der Zeitentwicklung eines Dichteoperators im Schrödingerbild, der den Zustand des Systems beschreibt. vertauscht. So würde das für die Heisenberg-Gleichung als Bewegungsgleichung eines Operators im Heisenbergbild gelten; wir reden hier jedoch von der Zeitentwicklung eines Dichteoperators im Schrödingerbild, der den Zustand des Systems beschreibt.
|
Danke, das hatte ich tatsächlich verwechselt.
Also ich schreib mal hin, wie ich das verstanden habe (nur den Ansatz, das stumpfe Ausrechnen bekomme ich dann hoffentlich alleine hin):
 = e^{-\frac{i}{\hbar}\hat{H}t} = e^{-i\omega\vec{\sigma}_xt} = \cos(-\omega t)+i(\vec{n}\vec{\sigma})\sin(-\omega t))
Dabei ist bei mir
}{=} \sigma_x)
Außerdem ist
^\dagger = \cos(-\omega t)-i(\vec{n}\vec{\sigma})\sin(-\omega t) )
Das setze ich dann ein in die Formel für die zeitentwickelte Dichtematrix. Die p_i bleiben dann einfach die von der Dichtematrix bei t=0 und so sollte ich am Ende eine 2x2 Matrix rausbekommen, deren Diagonaleinträge die Wahrscheinlichekeiten für a_1 und a_2 sind. Stimmt das so?
Danke für die Hilfe! |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 18. Jan 2022 10:02 Titel: index_razor Verfasst am: 18. Jan 2022 10:02 Titel: |
 |
|
Ja, wie gesagt, der Zeitentwicklungsoperator ist
 = \cos(\omega t) - i\sin(\omega t)(|a_1\rangle\langle a_2| + |a_2 \rangle \langle a_1|)=\cos(\omega t) - \frac{i}{\omega\hbar}\sin(\omega t)H.)
Dafür solltest du vielleicht noch eine Begründung angeben. Aber ich denke mehr Formalismus mußt du eigentlich für die Aufgabe nicht extra einführen.
Damit rechnest du jetzt also
 = U(t)\rho_0 U^\dagger(t))
in der  -Basis aus. Die Wahrscheinlichkeit -Basis aus. Die Wahrscheinlichkeit  ist der Koeffizient vor ist der Koeffizient vor  . . |
|
 |
Physiker1.1
Anmeldungsdatum: 14.11.2021
Beiträge: 19
|
 Physiker1.1 Verfasst am: 18. Jan 2022 21:04 Titel: Physiker1.1 Verfasst am: 18. Jan 2022 21:04 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | Ja, wie gesagt, der Zeitentwicklungsoperator ist
 = \cos(\omega t) - i\sin(\omega t)(|a_1\rangle\langle a_2| + |a_2 \rangle \langle a_1|)=\cos(\omega t) - \frac{i}{\omega\hbar}\sin(\omega t)H.)
Dafür solltest du vielleicht noch eine Begründung angeben. Aber ich denke mehr Formalismus mußt du eigentlich für die Aufgabe nicht extra einführen. |
Alles klar, dann vielen Dank für die Hilfe! Die Relation werde ich bei Gelegenheit beweisen, wenn ich die Zeit dafür finde. Ich denke mal das geht über die Potenzreihenentwicklung der e-Funktion. Das hattest Du ja auch weiter oben schonmal angerissen. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
 TomS Verfasst am: 18. Jan 2022 22:59 Titel: TomS Verfasst am: 18. Jan 2022 22:59 Titel: |
 |
|
| Physiker1.1 hat Folgendes geschrieben: | | Ich denke mal das geht über die Potenzreihenentwicklung der e-Funktion. |
Genau.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
|















