| Autor |
Nachricht |
Chillosaurus
Anmeldungsdatum: 07.08.2010
Beiträge: 2440
|
 Chillosaurus Verfasst am: 21. Feb 2011 00:27 Titel: Zeitentwicklung |
 |
|
Folgende Frage:
Der Hamiltonion ist bekannt:
 . Die Zustände  bilden eine vollständige Orthonormalbasis.
Nun soll die Zeitentwicklung  \right> ) in Termen der beiden Basiszustände angegeben werden. Dabei ist  \right> =\left| 1 \right> ) .
Normalerweise würde ich den Zeitentwicklungsoperator auf meine Darstellung der Wellenfunktion wirken lassen. Hier ist jedoch das Problem, dass in diesem Fall das System dann doch immer im Zustand 1 verbleiben würde.
Als Hinweis ist noch gegeben, dass eine Reihenentwicklung eventuell nützlich sein könnte.
Kann mir jemand weiterhelfen? |
|
 |
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18046
|
| TomS Verfasst am: 21. Feb 2011 00:40 Titel: |
|
|
M.E. solltest du den Zeitentwicklungsoperator exp(-iHt) mittels Taylorentwicklung berechnen. Die geraden Potenzen von (-iHt) sind dabei proportional zur Einheitsmatrix, die ungeraden wiederum proportional zu H. Diese Potenzen kannst du nun so sortieren, so dass du Sinus und Cosinus-Reihe erhältst, einmal mit einem Vorfaktor gleich Eins, einmal mit H. Damit ist der Zeitenwicklungsoperator exp(-iHt) im wesentlichen eine SU(2) Drehung deiner Basisvektoren |1> und |2>, die Zeit t geht dabei in den Drehwinkel ein.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
| pressure Verfasst am: 21. Feb 2011 08:44 Titel: |
|
|
In wie weit sind denn die beiden Zustände auch Eigenvektoren(/Zustände) zum Hamiltonoperator ?
Zuletzt bearbeitet von pressure am 21. Feb 2011 10:24, insgesamt einmal bearbeitet |
|
|
Chillosaurus
Anmeldungsdatum: 07.08.2010
Beiträge: 2440
|
| Chillosaurus Verfasst am: 21. Feb 2011 10:11 Titel: |
|
|
| pressure hat Folgendes geschrieben: | | In wie weit sind den die beiden Zustände auch Eigenvektoren(/Zustände) zum Hamiltonoperator ? |
Die gehen über Kreuz.
H|1>=h/2Pi |2>, H|2>=h/2Pi |1>
Die Idee mit der Taylorreihe hört sich vielversprechend an. Die werde ich gleich mal austesten.
-----------------------------------------------------------------
Ausgetestet: schaut gut aus:
 \right> =cos(t)\left| 1 \right> +i sin(t) \left| 2 \right> )
Somit ist die Wahrscheinlichkeit, dass zur Zeit t der Zustand |2> vorliegt:
 \right> |²=sin²(t))
Zuletzt bearbeitet von Chillosaurus am 21. Feb 2011 10:34, insgesamt einmal bearbeitet |
|
|
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
| pressure Verfasst am: 21. Feb 2011 10:21 Titel: |
|
|
Also:
Dann kannst du alternativ zu der Methode von TomS, die recht lehrreich ist, auch die Eigenzustände von H bestimmen und dann die beiden Zustände als Linearkombination der Eigenzustände schreiben. Beim Anwenden des Zeitpropagator darfst du dann jeweils H durch den entsprechenden Eigenwert ersetzen. |
|
|
Chillosaurus
Anmeldungsdatum: 07.08.2010
Beiträge: 2440
|
| Chillosaurus Verfasst am: 21. Feb 2011 10:42 Titel: |
|
|
| pressure hat Folgendes geschrieben: | | [...] Dann kannst du [...]die beiden Zustände als Linearkombination der Eigenzustände schreiben. Beim Anwenden des Zeitpropagator darfst du dann jeweils H durch den entsprechenden Eigenwert ersetzen. |
Das klappt genau so - schön, vielen Dank. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18046
|
| TomS Verfasst am: 21. Feb 2011 10:48 Titel: |
|
|
| Chillosaurus hat Folgendes geschrieben: |
Ausgetestet: schaut gut aus:
Somit ist die Wahrscheinlichkeit, dass zur Zeit t der Zustand |2> vorliegt:
|
Irgendwie fehlt aber das h/2pi.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
| pressure Verfasst am: 21. Feb 2011 11:13 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | Irgendwie fehlt aber das h/2pi. |
Das sollte sich mit dem 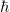 im Zeitpropagator kürzen, das du in deinem Beitrag weggelassen hast.
Vielleicht kommt die Verwirrung dadurch, dass die Dimension vom Hamiltonian falsch ist. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18046
|
| TomS Verfasst am: 21. Feb 2011 11:19 Titel: |
|
|
Ach so, das h soll tatsächlich die Plancksche Konstante sein.
Ich war etwas verwirrt, weil ich dachte, dass explizit ein Parameter der Dimension 'Energie' vorkommen müsste und hatte das mit h identifiziert.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
|
Registrieren
Login
FAQ
Suchen
