| Autor |
Nachricht |
taxus1
Anmeldungsdatum: 05.11.2016
Beiträge: 17
|
 taxus1 Verfasst am: 12. Jan 2017 19:02 Titel: Die Drehachse beim Garnrollen Problem taxus1 Verfasst am: 12. Jan 2017 19:02 Titel: Die Drehachse beim Garnrollen Problem |
 |
|
Hallo,
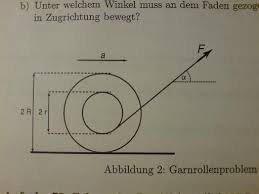
es geht um das sog. "Garnrollen-Problem". Man hat eine Garnrolle auf die ein Faden aufgewickelt ist. Dieser Faden wird nun gezogen. Je nach dem, in welchem Winkel der Faden gezogen wird, rollt die Rollt vor oder zurück.
Die Aufgabe ist das Drehmoment auf die Rolle zu berechnen.
Mein Problem ist, dass bei allen Rechnungen die man findet, als Drehachse immer der Aufliege-Punkt der Rolle genommen wird. Denn eigentlich kann sie sich ja gar nicht um diesen Punkt drehen, da der Boden sie daran hindert. Und wenn man sich den Rollprozess anschaut, sieht es ja auch eher so aus, als drehe sich die Spule um den Mittelpunkt.
Frage 1: Warum wird als Drehachse der Berührungspunkt mit dem Boden genommen und nicht einfach der Mittelpunkt?
Frage 2: Wie "verwandelt" sich die Drehbewegung um den Berührungspunkt, die durch den Boden unmöglich ist, in eine Drehbewegung um den Mittelpunkt, die man dann ja auch zu sehen bekommt?
| Beschreibung: |
|
| Dateigröße: |
5.23 KB |
| Angeschaut: |
2465 mal |
|
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 12. Jan 2017 19:52 Titel: VeryApe Verfasst am: 12. Jan 2017 19:52 Titel: |
 |
|
Dir wird vielleicht nicht entgangen sein, daß man in der Statik jeden x beliebigen Drehpunkt für Momente betrachten kann und immer richtig rechnet, bzw kommt immer dasselbe raus.
Das funktioniert genauso in der Dynamik, wenn man die Dalembertsche Trägheitskraft mitbetrachtet, weil die summe inklusive dieser Kraft null.
Ist die Summe alle Kräfte null dann ist die Summe aller Kräfte mal deren Normalabstand zu irgend,einen Bezugspunkt immer gleich also derselbe Wert, ohne das ich jetzt hier einen Beweis dazuschreibe, daß habe ich schon paar Mal hiergemacht.
Betrachtest du diese Dalembertkraft nicht mit, dann mußt du dieses Fehlen ausgleichen über das Trägheitsmoment.
Das machen die in der Physik.
Das funktioniert wenn Drehung um den Schwerpunkt und die Translation des Schwerpunktes miteinander auf den Bezugspunkt gekoppelt sind und über eine einheitliche Rotationgröße wie alpha , omega angegeben werden können.
Das Trägheitsmoment ändert sich zu so einen Bezugspunkt genau um die Gesamtmasse mal den Normalabstand zum Quadrat (Normalabsand auf die Schwerpunktsbeschleunigung).
Prinzipiell kann man aber jeden xbeliebigen Bezugspunkt betrachten wenn man ansetzt

Is bleibt auf jeden Bezugspunkt gleich
r_{s} Normalabstand auf die Schwerpunktsbeschleunigung zum Bezugspunkt ändert sich.
für den Fall der Koppelung kann man a_{s} ersetzen mit alpha*r_(s)
dann gilt

und

das wäre der Steinerverschiebesatz
Frage 1) das ist, wenn du den meinen Text verstanden hast, Geschmackssache
Frage 2)
bei einer Drehung um den Abrollpunkt betrachtet man das ganze nur als Drehung über eine unendlich kleine Zeitdauer, danach wird für das nächste delta t wieder ein neuer Abrollpunkt betrachtet.
das führt mathematisch zum selben Ergebnis, wie wenn du es so betrachtest wie du es siehst.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
taxus1
Anmeldungsdatum: 05.11.2016
Beiträge: 17
|
 taxus1 Verfasst am: 13. Jan 2017 21:05 Titel: taxus1 Verfasst am: 13. Jan 2017 21:05 Titel: |
 |
|
Danke für deine Antwort! Mir ist allerdings immer noch nicht so ganz klar, wie diese "Transformation" vonstatten geht:
Rotation um Auflagepunkt = Rotation um Mittelpunkt + Translationsbewegung des Mittelpunkts
| VeryApe hat Folgendes geschrieben: |
Das funktioniert wenn Drehung um den Schwerpunkt und die Translation des Schwerpunktes miteinander auf den Bezugspunkt gekoppelt sind und über eine einheitliche Rotationgröße wie alpha , omega angegeben werden können.
|
Wie kann man das auf den Bezugspunkt koppeln? Was heißt das überhaupt?
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 13. Jan 2017 21:50 Titel: VeryApe Verfasst am: 13. Jan 2017 21:50 Titel: |
 |
|
| Zitat: | | Rotation um Auflagepunkt = Rotation um Mittelpunkt + Translationsbewegung des Mittelpunkts |
Wenn der Massenmittelpunkt sich bewegt, dann kann man sich vorstellen jeder Massepunkt des Körpers bewegt sich genau mit der Geschwindigkeit des Massenmittelpunktes zusätzlich führt aber jeder Massepunkt noch eine Rotationsbewegung um den Massenmittelpunkt, was sich zu ersteren Geschwindigkeit hinzuaddiert.
dann betrachte doch mal die Addition beider Geschwindigkeiten für ein paar Massepunkte des Körpers und vergleich sie mit den Geschwindigkeiten die du für die Massepunkte erhälst wenn du dir vorstellst sie würden um den Abrollpunkt rotieren.
| Zitat: | Wie kann man das auf den Bezugspunkt koppeln? Was heißt das überhaupt?
|
damit meine ich, das der Massenmittelpunkt in Abhängigkeit zur Winkelbeschleunigung um den Schwerpunkt beschleunigt. und zwar nach der Rollbedingung.
 * r_{s} )
Das ist doch nur ein Speziallfall.
Es gibt keinen Grund warum das immer so sein muß unter Gleitreibung wär das nicht der Fall. Da könnte der Schwerpunkt stärker an Geschwindigkeit gewinnen als die rotation nachkommt.,
Es besteht nicht immer die Möglichkeit die Beschleunigung a(s) als funktion der Winkelbeschleunigung um den Schwerpunkt auszudrücken.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
|
|
















