| Autor |
Nachricht |
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
 Amateurphysiker Verfasst am: 03. Apr 2016 17:00 Titel: Effektives Potential- Stabilität von Kreisbahnen Amateurphysiker Verfasst am: 03. Apr 2016 17:00 Titel: Effektives Potential- Stabilität von Kreisbahnen |
 |
|
Hallo, ich muss das effektive Potential bestimmen für ein Zentralkraftfeld. Im ersten Schritt habe ich versucht das Potential selbst zu bestimmen, aber irgendwie hab ich das Gefühl, dass es falsch ist. Kann vielleicht jemand drauf schauen?
Danke!
| Beschreibung: |
|

Download |
| Dateiname: |
Ansatz.jpg |
| Dateigröße: |
723.73 KB |
| Heruntergeladen: |
346 mal |
| Beschreibung: |
|

Download |
| Dateiname: |
Aufgabe - Stabilität von Kreisbahnen.png |
| Dateigröße: |
71.62 KB |
| Heruntergeladen: |
366 mal |
|
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 03. Apr 2016 17:12 Titel: jh8979 Verfasst am: 03. Apr 2016 17:12 Titel: |
 |
|
Am Ende steht zwar das richtige da, aber die Schritte dahin sind nicht korrekt aufgeschrieben. Überleg Dir nochmal was genau da für ein Integral stehen muss.
Hier siehst Du es etwas ausführlicher durchgerechnet für das Gravitationspotential:
https://en.wikipedia.org/wiki/Potential_energy#Derivation
|
|
 |
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
 Amateurphysiker Verfasst am: 03. Apr 2016 17:57 Titel: Amateurphysiker Verfasst am: 03. Apr 2016 17:57 Titel: |
 |
|
Ok ich habs nochmal versucht analog umzuschreiben. Passt das so? Aber wie kann ich nun das Integral berechnen ohne v zu kennen?
| Beschreibung: |
|

Download |
| Dateiname: |
IMG_20160403_175504.jpg |
| Dateigröße: |
752.02 KB |
| Heruntergeladen: |
269 mal |
|
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 03. Apr 2016 17:59 Titel: jh8979 Verfasst am: 03. Apr 2016 17:59 Titel: |
 |
|
| Amateurphysiker hat Folgendes geschrieben: | | Ok ich habs nochmal versucht analog umzuschreiben. Passt das so? Aber wie kann ich nun das Integral berechnen ohne v zu kennen? |
Wie können die das da im Wiki-Link?
|
|
 |
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 03. Apr 2016 18:37 Titel: jh8979 Verfasst am: 03. Apr 2016 18:37 Titel: |
 |
|
| Amateurphysiker hat Folgendes geschrieben: | Ohje..da würde ich ja nie drauf kommen das alles so umzuschreiben :/ und wieso fällt das  von 1 auf 2 (Vgl. Anhang) raus? von 1 auf 2 (Vgl. Anhang) raus? |
Weil der zugehörige Vektor senkrecht auf e_r steht.
|
|
 |
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
 Amateurphysiker Verfasst am: 03. Apr 2016 18:55 Titel: Amateurphysiker Verfasst am: 03. Apr 2016 18:55 Titel: |
 |
|
Achso ok klar.
Passt mein V und V_eff jetzt so? Falls ja, wie kann ich rausfinden fuer welche Potenz V_eff ein Minimum hat?
| Beschreibung: |
|

Download |
| Dateiname: |
IMG_20160403_185239.jpg |
| Dateigröße: |
549.64 KB |
| Heruntergeladen: |
262 mal |
|
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 03. Apr 2016 19:01 Titel: jh8979 Verfasst am: 03. Apr 2016 19:01 Titel: |
 |
|
| Amateurphysiker hat Folgendes geschrieben: | Achso ok klar.
Passt mein V und V_eff jetzt so? Falls ja, wie kann ich rausfinden fuer welche Potenz V_eff ein Minimum hat? |
1. Ich weiss nicht was V(r) bei dir sein soll (r=r1 oder r=r2?). Das eine ergibt ein falsches Vorzeichen Ich würde das Potential (für n!=1) sowieso so normieren, dass es es im Unendlichen verschwindet. (Dabei fällt mir ein, der Fall n=1 muss gesondert betrachtet werden.)
2. Wie Wie findest Du denn sonst raus, ob eine Funktion ein Minimum besitzt?
|
|
 |
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
 Amateurphysiker Verfasst am: 03. Apr 2016 20:06 Titel: Amateurphysiker Verfasst am: 03. Apr 2016 20:06 Titel: |
 |
|
| jh8979 hat Folgendes geschrieben: |
1. Ich weiss nicht was V(r) bei dir sein soll (r=r1 oder r=r2?). Das eine ergibt ein falsches Vorzeichen Ich würde das Potential (für n!=1) sowieso so normieren, dass es es im Unendlichen verschwindet. (Dabei fällt mir ein, der Fall n=1 muss gesondert betrachtet werden.)
|
D.h. ich setze einen der beiden Terme einfach gleich 0?
| jh8979 hat Folgendes geschrieben: |
2. Wie Wie findest Du denn sonst raus, ob eine Funktion ein Minimum besitzt? |
Ableiten und Nullstelle ermitteln?  In dem Fall also nach n ableiten? In dem Fall also nach n ableiten?
|
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 03. Apr 2016 20:09 Titel: jh8979 Verfasst am: 03. Apr 2016 20:09 Titel: |
 |
|
| Amateurphysiker hat Folgendes geschrieben: |
D.h. ich setze einen der beiden Terme einfach gleich 0?
|
Vorzugsweise den richtigen.
| Zitat: |
Ableiten und Nullstelle ermitteln?  In dem Fall also nach n ableiten? In dem Fall also nach n ableiten? |
Erste Frage: Ja. Zweite Frage: Nein, nach r. Du willst ja wissen ob Die Funktion als Funktion von r ein Minimum hat (was von n abhängt).
|
|
 |
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
 Amateurphysiker Verfasst am: 03. Apr 2016 21:09 Titel: Amateurphysiker Verfasst am: 03. Apr 2016 21:09 Titel: |
 |
|
| jh8979 hat Folgendes geschrieben: |
Vorzugsweise den richtigen.
|
In wie fern macht das einen Unterschied, bzw. was ist richtig? Das Potential sagt mir doch wie viel Potentielle Energie in einem Punkt relativ zu dem anderen steckt oder? D.h. wo ich den Nullpunkt setze ist doch beliebig oder nicht?
| Zitat: |
Erste Frage: Ja. Zweite Frage: Nein, nach r. Du willst ja wissen ob Die Funktion als Funktion von r ein Minimum hat (was von n abhängt). |
Ja macht Sinn!
Zuletzt bearbeitet von Amateurphysiker am 03. Apr 2016 21:47, insgesamt einmal bearbeitet |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 03. Apr 2016 21:13 Titel: jh8979 Verfasst am: 03. Apr 2016 21:13 Titel: |
 |
|
| Amateurphysiker hat Folgendes geschrieben: |
In wie fern macht das einen Unterschied, bzw. was ist richtig? Das Potential sagt mir doch wie viel Potentielle Energie in einem Punkt relativ zu dem anderen steckt oder? D.h. wo ich den Nullpunkt setze ist doch beliebig oder nicht?
|
Es macht aber einen Unterschied in welche Richtung das Potential zu- oder abnimmt, d.h. im Vorzeichen. Und das Vorzeichen ändert die Richtung der resultierenden Kraft, ist also physikalisch relevant.
|
|
 |
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
 Amateurphysiker Verfasst am: 03. Apr 2016 22:00 Titel: Amateurphysiker Verfasst am: 03. Apr 2016 22:00 Titel: |
 |
|
Hmm ok, leider hab ich keine Ahnung woher ich jetzt weiss was richtig ist. Ich weiss, dass die Kraft radial nach Innen zeigt. Aber woher weiss ich ob das Potential von Punkt 1 zu Punkt 2 oder andersherum zu oder abnimmt?
Ich hab jetzt mal V_eff abgeleitet. Aber wie komme ich damit auf die gesuchte Potenz!? Sorry für die vielen Fragen...
| Beschreibung: |
|

Download |
| Dateiname: |
IMG_20160403_215650.jpg |
| Dateigröße: |
684.98 KB |
| Heruntergeladen: |
263 mal |
|
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 03. Apr 2016 22:03 Titel: jh8979 Verfasst am: 03. Apr 2016 22:03 Titel: |
 |
|
|
Das sind beides Fragen, die Du selber beantworten können musst.
|
|
 |
E=mc²
Anmeldungsdatum: 24.06.2014
Beiträge: 494
|
 E=mc² Verfasst am: 03. Apr 2016 22:32 Titel: E=mc² Verfasst am: 03. Apr 2016 22:32 Titel: |
 |
|
Wie ist denn das Potenzial definiert?
schaue das mal in einem deiner Bücher oder zB hier oder hier nach!
Die Kraft wirkt immer in Richtung niedrigeres Potenzial. Bei deinem Beispiel zeigt die Kraft radial nach innen. Wo ist also das Potenzial niedriger?
|
|
 |
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
 Amateurphysiker Verfasst am: 04. Apr 2016 13:09 Titel: Amateurphysiker Verfasst am: 04. Apr 2016 13:09 Titel: |
 |
|
Ok ich verstehe, dass das Potential nach aussen hin zunimmt (da die Kräfte nach innen gerichtet sind). Da der Radius im Potential exponential im Nenner auftaucht, heisst das, dass der Bruch mit Zunahme von r abnimmt. D.h. der Bruch müsste negativ sein um mit Zunahme des Nenners zuzunehmen!?
Und was mache ich jetzt mit meiner Ableitung des effektiven Potentials? Ich komme mit der Gleichung im orangenen Kasten (siehe Anhang) nicht weiter, ist das überhaupt richtig soweit?
Danke!!
| Beschreibung: |
|

Download |
| Dateiname: |
IMG_20160404_130600.jpg |
| Dateigröße: |
593.02 KB |
| Heruntergeladen: |
259 mal |
|
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 04. Apr 2016 14:27 Titel: jh8979 Verfasst am: 04. Apr 2016 14:27 Titel: |
 |
|
Nein, da fehlt schon wieder was (was ganz am Anfang mal da war und dann verloren ging).
Also, mal Schritt für Schritt:
1. Die Kraft ist
}{r^{n-1}} \right)) fuer fuer 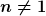 , ,
d.h. ist das effektive Potential ist in diesem Fall
}{r^{n-1}} )
2. Ableiten und Null setzen ergibt
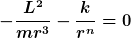 also also  . .
3. Fuer n=3 hat gilt diese Gleichung offensichtlich nie (es sei denn L=0, aber das würde nie zu einer Kreisbahn führen, da das Potential dann nie ein Minimum für endliche r besitzt). Für  folgt folgt ^{\frac{1}{3-n}}) . .
4. Ueberpruefen ob der gefundene Wert in 3 ein Minimum ist: Die zweite Ableitung ist

ausgewertet im gefundenen Wert von 3 ergibt :
 \left(\frac{L^2}{k m.} \right)^{\frac{n+1}{n-3}} )
(hier muss man jetzt bisschen die Potenzen vereinfachen, um zu sehen dass in beiden Termin dieselben Potenzen übrig bleiben, z.B. für L im ersten Term ^{-\frac{4}{3-n}} = (L^2)^{-\frac{n+1}{3-n}}) für die anderen Konstanten erhält man ähnliches.) für die anderen Konstanten erhält man ähnliches.)
Daraus folgt, dass n nicht größer als 3 sein darf, da man sonst ein Maximum und kein Minimum hat.
5. Der Fall n=1 fehlt noch. Für n=1 gilt:
)
fuer eine beliebigen Referenzradius r0, der in diesem Fall weder Null noch Unendlich (wie für n!=1 oben gewählt) sein darf.
Ableiten und Nullsetzen ergibt  und das in die zweite Ableitung eingesetzt und das in die zweite Ableitung eingesetzt
 , ,
d.h. hier gibt es auch ein Minimum.
Zusammengefasst:
 liefert fuer alle n echt kleiner als 3 (einschliesslich negative n) ein Minimum im effektiven Potential, d.h. es sind stabile(!) Kreisbahnen möglich. liefert fuer alle n echt kleiner als 3 (einschliesslich negative n) ein Minimum im effektiven Potential, d.h. es sind stabile(!) Kreisbahnen möglich.
PS: Ich halte diese Aufgabe zwar für etwas länglich, aber in einer Klausur durchaus möglich (je nach vorhandener Zeit und möglichen noch zusätzlichen gegeben Tipps/Zwischenergebnissen).
|
|
 |
Amateurphysiker
Anmeldungsdatum: 13.11.2015
Beiträge: 307
|
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 04. Apr 2016 18:49 Titel: jh8979 Verfasst am: 04. Apr 2016 18:49 Titel: |
 |
|
Im zweiten Term steht es gleich richtig da. Im ersten gilt
})^{-4} = k^{\frac{-4}{n-3}})
und
}{n-3} = 1 - \frac{n+1}{n-3}) . .
|
|
 |
|
















 In dem Fall also nach n ableiten?
In dem Fall also nach n ableiten?