| Autor |
Nachricht |
Claudini95
Anmeldungsdatum: 31.05.2015
Beiträge: 126
|
|
 |
Claudini95
Anmeldungsdatum: 31.05.2015
Beiträge: 126
|
 Claudini95 Verfasst am: 11. Feb 2016 21:39 Titel: Claudini95 Verfasst am: 11. Feb 2016 21:39 Titel: |
 |
|
Ich bin mir einfach an den zwei Knackpunkten unsicher und komme deswegen leider nicht weiter  Es ist zum Haare rausreißen Es ist zum Haare rausreißen 
Claudia
|
|
 |
David123456
Gast
|
 David123456 Verfasst am: 11. Feb 2016 22:07 Titel: David123456 Verfasst am: 11. Feb 2016 22:07 Titel: |
 |
|
Für deine DGL:
Du könntest deine Gleichung
=-L\frac{di_{l}(t)}{dt})
So umstellen, dass auf einer Seite dt steht und auf der anderen Seite di_{l}(t)
(Man spricht hier von trennen der Variablen)
Dadurch würde sich folgende Gleichung ergeben
}{i_{l}(t)*R})
bzw. zur besseren Übersicht:
}{i_{l}(t)})
Jetzt solltest du dein Integral problemlos anwenden können.
MFG
|
|
 |
Claudini95
Anmeldungsdatum: 31.05.2015
Beiträge: 126
|
 Claudini95 Verfasst am: 11. Feb 2016 22:12 Titel: Claudini95 Verfasst am: 11. Feb 2016 22:12 Titel: |
 |
|
Hey David,
Man könnte das  aber auch auf der anderen Seite stehen lassen? aber auch auf der anderen Seite stehen lassen?
}{i_{l}(t)})
Und jetzt integrieren, aber das Integral und das dt heben sich auf?
Claudia
|
|
 |
David123456
Gast
|
 David123456 Verfasst am: 11. Feb 2016 22:14 Titel: David123456 Verfasst am: 11. Feb 2016 22:14 Titel: |
 |
|
|
Ja das würde auch so gehen
|
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 11. Feb 2016 22:17 Titel: Re: DGL, LaPlace-Transformation + homogene,partikuläre Lösun jh8979 Verfasst am: 11. Feb 2016 22:17 Titel: Re: DGL, LaPlace-Transformation + homogene,partikuläre Lösun |
 |
|
| Claudini95 hat Folgendes geschrieben: |
 = R L \cdot s \cdot i_L (s) + R \cdot i_L (s) )
|
Hier musst Du die Laplace-Transformierte von u_e einsetzen, dann das ganze nach i_L umformen und dann zuruecktransformieren.
|
|
 |
Claudini95
Anmeldungsdatum: 31.05.2015
Beiträge: 126
|
 Claudini95 Verfasst am: 11. Feb 2016 22:30 Titel: Re: DGL, LaPlace-Transformation + homogene,partikuläre Lösun Claudini95 Verfasst am: 11. Feb 2016 22:30 Titel: Re: DGL, LaPlace-Transformation + homogene,partikuläre Lösun |
 |
|
Okay. Eins nach dem anderem.
Wenn das dann integriert bekommt man dann:
)
Aber Formal ist da was falsch wenn da schon vorher das 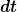 steht? Das kommt ja mit dem Integral. steht? Das kommt ja mit dem Integral.
| jh8979 hat Folgendes geschrieben: |
Hier musst Du die Laplace-Transformierte von u_e einsetzen, dann das ganze nach i_L umformen und dann zuruecktransformieren. |
 = R L \cdot s \cdot i_L (s) + R \cdot i_L (s) )
Die Laplace-Transformierte ist ja von ) dann dann 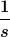
Also  + R \cdot i_L (s) )
Umstellen:  = \frac{1}{s(R L \cdot s + R)})
Das würde die Form dann der abklingenden e-Funktion annehmen.
Oder?
Vielen Dank an Euch beide!
Claudia
|
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 11. Feb 2016 22:43 Titel: Re: DGL, LaPlace-Transformation + homogene,partikuläre Lösun jh8979 Verfasst am: 11. Feb 2016 22:43 Titel: Re: DGL, LaPlace-Transformation + homogene,partikuläre Lösun |
 |
|
| Claudini95 hat Folgendes geschrieben: |
Die Laplace-Transformierte ist ja von ) dann dann 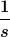
Also  + R \cdot i_L (s) )
Umstellen:  = \frac{1}{s(R L \cdot s + R)})
Das würde die Form dann der abklingenden e-Funktion annehmen.
|
Nicht raten.
|
|
 |
David123456
Gast
|
 David123456 Verfasst am: 11. Feb 2016 22:44 Titel: David123456 Verfasst am: 11. Feb 2016 22:44 Titel: |
 |
|
|
Mh ich kann dir gleich einen anderen Lösungsweg geben. Wobei ich mich gerade Frage warum du mit i_l rechnest wenn die Aufgabe für den Kondensator ausgelegt ist. Sollst du jetzt die DGL der Spule bestimmen?
|
|
 |
David123456
Gast
|
 David123456 Verfasst am: 11. Feb 2016 22:45 Titel: David123456 Verfasst am: 11. Feb 2016 22:45 Titel: |
 |
|
Ups verlesen... nehme es zurück 
|
|
 |
Claudini95
Anmeldungsdatum: 31.05.2015
Beiträge: 126
|
 Claudini95 Verfasst am: 11. Feb 2016 22:48 Titel: Re: DGL, LaPlace-Transformation + homogene,partikuläre Lösun Claudini95 Verfasst am: 11. Feb 2016 22:48 Titel: Re: DGL, LaPlace-Transformation + homogene,partikuläre Lösun |
 |
|
| jh8979 hat Folgendes geschrieben: |
Nicht raten. |
Wieso raten? Hm. Die Spannungsfunktion ) ist doch die Sprungfunktion. Und die Sprungfunktion ist transformiert 1 durch s? Da wir keinen Vorfaktor haben bzw. eventuell ist doch die Sprungfunktion. Und die Sprungfunktion ist transformiert 1 durch s? Da wir keinen Vorfaktor haben bzw. eventuell  da da 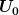 die Auslenkung ist, aber für die haben wir keinen konkreten Wert. die Auslenkung ist, aber für die haben wir keinen konkreten Wert.
Claudia
|
|
 |
David123456
Gast
|
 David123456 Verfasst am: 11. Feb 2016 23:00 Titel: Re: DGL, LaPlace-Transformation + homogene,partikuläre Lösun David123456 Verfasst am: 11. Feb 2016 23:00 Titel: Re: DGL, LaPlace-Transformation + homogene,partikuläre Lösun |
 |
|
| Claudini95 hat Folgendes geschrieben: | Okay. Eins nach dem anderem.
Wenn das dann integriert bekommt man dann:
)
Aber Formal ist da was falsch wenn da schon vorher das 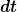 steht? Das kommt ja mit dem Integral. steht? Das kommt ja mit dem Integral.
|
Was genau meinst du mit Formal falsch? Wenn du über dt integrierst erhälst du immer t + const. .
|
|
 |
Claudini95
Anmeldungsdatum: 31.05.2015
Beiträge: 126
|
 Claudini95 Verfasst am: 11. Feb 2016 23:05 Titel: Claudini95 Verfasst am: 11. Feb 2016 23:05 Titel: |
 |
|
Also wenn wir die Gleichung haben:
}{i_{l}(t)})
Und dann integrieren. Bekommen wir doch:
}{i_{l}(t)} dt)
Ein Integralzeichen liefert doch immer das Element dt mit sich. Rechts vom Gleichheitszeichen passt es ja, aber links? Kann man doch nicht eins streichen?
Claudia
|
|
 |
David123456
Gast
|
 David123456 Verfasst am: 11. Feb 2016 23:13 Titel: David123456 Verfasst am: 11. Feb 2016 23:13 Titel: |
 |
|
Achso, nein das ist nicht der Fall, du hast folgendes in deinem Integral stehen:

|
|
 |
David123456
Gast
|
 David123456 Verfasst am: 11. Feb 2016 23:14 Titel: David123456 Verfasst am: 11. Feb 2016 23:14 Titel: |
 |
|
|
Bzw auf der rechten Seite integrierst du über di und nicht über dt.
|
|
 |
Claudini95
Anmeldungsdatum: 31.05.2015
Beiträge: 126
|
 Claudini95 Verfasst am: 11. Feb 2016 23:17 Titel: Claudini95 Verfasst am: 11. Feb 2016 23:17 Titel: |
 |
|
| David123456 hat Folgendes geschrieben: | Achso, nein das ist nicht der Fall, du hast folgendes in deinem Integral stehen:
 |
Ja. Und was ist mit dem  was noch links vor dem was noch links vor dem  steht? Das kann doch nicht wegfallen da ist irgendwo ein Fehler. Ja stimmt links bekommen wir ein steht? Das kann doch nicht wegfallen da ist irgendwo ein Fehler. Ja stimmt links bekommen wir ein 
Claudia
|
|
 |
David123456
Gast
|
 David123456 Verfasst am: 11. Feb 2016 23:30 Titel: David123456 Verfasst am: 11. Feb 2016 23:30 Titel: |
 |
|
|
Das ist das dt was am Integral steht. Wie genau ich das verständlich erklären kann weiß ich gerade nicht.
|
|
 |
David123456
Gast
|
 David123456 Verfasst am: 11. Feb 2016 23:53 Titel: David123456 Verfasst am: 11. Feb 2016 23:53 Titel: |
 |
|
|
Aber egal auf welche weise du das Integral betrachtest ändert dies nichts am ergebnis, was jetzt die mathematische korrekte schreibweise für den Fall ist ,weiß ich leider net
|
|
 |
Claudini95
Anmeldungsdatum: 31.05.2015
Beiträge: 126
|
 Claudini95 Verfasst am: 12. Feb 2016 00:17 Titel: Claudini95 Verfasst am: 12. Feb 2016 00:17 Titel: |
 |
|
Nun irgendwie ist die Formalität nicht 100% gegeben bzw. ich sehe es nicht.
Danke!
Die Frage ist noch was ich bei der Transformation falsch gemacht habe mh.
Claudia
|
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
|
 |
|
















 Es ist zum Haare rausreißen
Es ist zum Haare rausreißen 