| Autor |
Nachricht |
GalvanisFrösche
Anmeldungsdatum: 05.06.2015
Beiträge: 22
|
 GalvanisFrösche Verfasst am: 05. Jun 2015 21:07 Titel: Masse-Feder-System GalvanisFrösche Verfasst am: 05. Jun 2015 21:07 Titel: Masse-Feder-System |
 |
|
Meine Frage:
Hallo Physiker,
ich bin neu hier und habe ein Problem mit folgender Aufgabe:
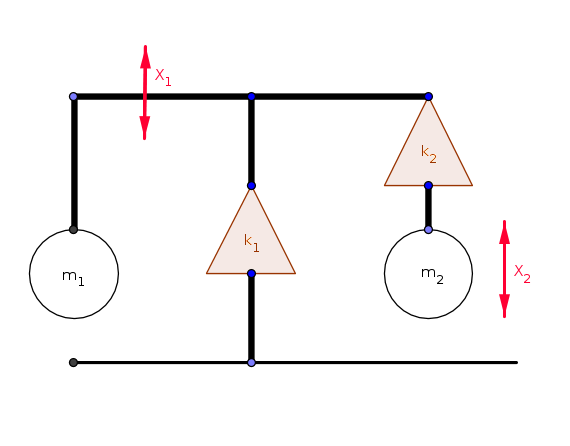
Eine Masse m_1 ist an eine Feder mit Ruhelänge a und Federkonstante k gebunden, die wiederum an eine Masse m2 gebunden ist. Die zweite Masse ist über eine identische Feder mit dem Boden verbunden. Die Massen können sich reibungsfrei entlang einer Stange senkrecht zum Boden bewegen und unterliegen der Schwerkraft.
Stellen Sie die Lagrange-Funktion des Systems auf und bestimmen Sie die Matrizen der kinetischen und der potentiellen Energie für Schwingungen um die Ruhelage.
Hier die Originalskizze der Aufgabenstellung:
 http://www.fotos-hochladen.net/uploads/sheet7verschoqwe72g0zfp.jpg http://www.fotos-hochladen.net/uploads/sheet7verschoqwe72g0zfp.jpg
Meine Ideen:
Die kinetische Energie:
 )
und die potentielle Energie:
^2 )
dann folgt die Lagrangefunktion:
 - \frac{k}{2} \left(x_2 - x_1\right)^2 )
Daraus folgt:

Daraus erhält man zwei Bewegungsgleichungen:

Leider weiss ich aus einer anderen Quelle dass die Bewegungsgleichungen lauten müssen:

Habe ich irgendwo einen Fehler gemacht?
Vielen Dank für jegliche Hilfe
|
|
 |
erkü

Anmeldungsdatum: 23.03.2008
Beiträge: 1414
|
 erkü Verfasst am: 06. Jun 2015 02:00 Titel: Re: Masse-Feder-System erkü Verfasst am: 06. Jun 2015 02:00 Titel: Re: Masse-Feder-System |
 |
|
| GalvanisFrösche hat Folgendes geschrieben: |
...
Leider weiss ich aus einer anderen Quelle dass die Bewegungsgleichungen lauten müssen:
 |

Woher soll laut der "anderen Quelle" die doppelte Federsteife 2k kommen ?
| Zitat: | Habe ich irgendwo einen Fehler gemacht?
|
Ich kann keinen grundsätzlichen Fehler sehen.
_________________
Das Drehmoment ist der Moment, wo es zu drehen anfängt. :punk: |
|
 |
GalvanisFrösche
Anmeldungsdatum: 05.06.2015
Beiträge: 22
|
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 06. Jun 2015 16:40 Titel: jh8979 Verfasst am: 06. Jun 2015 16:40 Titel: |
 |
|
Mal davon abgesehen von ein paar Tipp(?)fehlen in Deinen Bewegungsgleichungen:
Deine potentielle Energie ist falsch.
|
|
 |
GalvanisFrösche
Anmeldungsdatum: 05.06.2015
Beiträge: 22
|
 GalvanisFrösche Verfasst am: 06. Jun 2015 16:51 Titel: GalvanisFrösche Verfasst am: 06. Jun 2015 16:51 Titel: |
 |
|
Sry für den einen Tippfehler:

So solltes es lauten.
Wie lautet dann die potentielle Enerige, wenn nicht:
^2)
|
|
 |
Khaleb
Anmeldungsdatum: 01.05.2015
Beiträge: 64
|
 Khaleb Verfasst am: 06. Jun 2015 16:55 Titel: Wo ist die was in der hamiltonfunktion Khaleb Verfasst am: 06. Jun 2015 16:55 Titel: Wo ist die was in der hamiltonfunktion |
 |
|
1) wo steckt (im potential) Deiner lagrangefunktion die feder der masse m2
2) wo kommt in der potentiellen energie die ruhelage a der feder vor
3) wo kommt im potential die gravitation der erde vor?
Mir fehlt fas alles.
Am besten langsam vorgehen.
Potentielle energie der feder zwischen m2 und boden, potentielle energie der feder zwischen m1 und m2, potential der masse m2 auf grund der erdanziehung, potential der masse m1 auf grund der erdanziehung.
Zuletzt bearbeitet von Khaleb am 06. Jun 2015 17:02, insgesamt 2-mal bearbeitet |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 06. Jun 2015 16:59 Titel: jh8979 Verfasst am: 06. Jun 2015 16:59 Titel: |
 |
|
| GalvanisFrösche hat Folgendes geschrieben: |
Wie lautet dann die potentielle Enerige, wenn nicht:
^2) |
Was ist das denn für eine potentielle Energie, die Du hier hingeschrieben hast?
|
|
 |
GalvanisFrösche
Anmeldungsdatum: 05.06.2015
Beiträge: 22
|
 GalvanisFrösche Verfasst am: 06. Jun 2015 17:01 Titel: GalvanisFrösche Verfasst am: 06. Jun 2015 17:01 Titel: |
 |
|
1) Die Masse m_2 hat die Masse m.
2) Ich dachte die kommt erst in der Lösung der Bewegungsgleichung vor.. Keine Ahnung, wie könnte man die Ruhelage einbringen??
3)Im Potential könnte man in der Tat einfügen:
^2 - 2mga)
dann hätte man auch über a die Ruhelage eingebracht 
|
|
 |
GalvanisFrösche
Anmeldungsdatum: 05.06.2015
Beiträge: 22
|
 GalvanisFrösche Verfasst am: 06. Jun 2015 17:05 Titel: GalvanisFrösche Verfasst am: 06. Jun 2015 17:05 Titel: |
 |
|
Das Potential hatte ich mir folgendermaßen hergeleitet:

Wegen:

Daraus folgt:

Fehler?
und dann habe ich nur überlegt wie sich die Lage bei zwei bewegten Masse verändert und habe für 
|
|
 |
Khaleb
Anmeldungsdatum: 01.05.2015
Beiträge: 64
|
 Khaleb Verfasst am: 06. Jun 2015 17:06 Titel: Wann ist die feder entspannt.? Khaleb Verfasst am: 06. Jun 2015 17:06 Titel: Wann ist die feder entspannt.? |
 |
|
|
Welche bedingung müssen x1 und x2 erfüllen damit die feder zwischen m1 und m2 entspannt ist , also keine kraft ausübt und damit keine energie gespeichert hat ?
|
|
 |
GalvanisFrösche
Anmeldungsdatum: 05.06.2015
Beiträge: 22
|
 GalvanisFrösche Verfasst am: 06. Jun 2015 17:11 Titel: GalvanisFrösche Verfasst am: 06. Jun 2015 17:11 Titel: |
 |
|
|
Beide müssen sich in Ruhelage befinden...
|
|
 |
Khaleb
Anmeldungsdatum: 01.05.2015
Beiträge: 64
|
 Khaleb Verfasst am: 06. Jun 2015 17:14 Titel: Formel Khaleb Verfasst am: 06. Jun 2015 17:14 Titel: Formel |
 |
|
|
Kannst du das in eine formel fassen und in der angabe nachschauen ob die dir was darüber verrät?
|
|
 |
GalvanisFrösche
Anmeldungsdatum: 05.06.2015
Beiträge: 22
|
 GalvanisFrösche Verfasst am: 06. Jun 2015 17:23 Titel: Die einzelnen Potentiale GalvanisFrösche Verfasst am: 06. Jun 2015 17:23 Titel: Die einzelnen Potentiale |
 |
|
Potential Feder m_2 und Boden:

Potential Feder m_1 und m_2:

Potential m_2 Erdanziehung:

Potential m_1 Erdanziehung:

|
|
 |
Khaleb
Anmeldungsdatum: 01.05.2015
Beiträge: 64
|
 Khaleb Verfasst am: 06. Jun 2015 17:24 Titel: Falls das zu viel auf einmal ist Khaleb Verfasst am: 06. Jun 2015 17:24 Titel: Falls das zu viel auf einmal ist |
 |
|
|
Falls das noch zu viele schritte auf einmal sind: welche länge l soll die feder laut angabe haben, damit sie entspannt ist ? du verwechselst da was, a bezieht sich auf die feder ganz alleine, ohne gravitation oder so
|
|
 |
GalvanisFrösche
Anmeldungsdatum: 05.06.2015
Beiträge: 22
|
|
 |
Khaleb
Anmeldungsdatum: 01.05.2015
Beiträge: 64
|
 Khaleb Verfasst am: 06. Jun 2015 17:33 Titel: Stimmt Khaleb Verfasst am: 06. Jun 2015 17:33 Titel: Stimmt |
 |
|
|
Wie hängt die länge der feder zwischen m1 und m2 mit x1 und x2 zusammen? l = f(x1,x2) ? Also x1 ist die höhe der masse 1 über dem boden und x2 ist die höhe der masse 2 über dem boden und die feder ist an einem ende mit der masse 1 verbunden und am anseren ende mit der masse 2. Das ist jetzt unabhängig davon ob die feder entspannt ist oder nicht!
|
|
 |
Khaleb
Anmeldungsdatum: 01.05.2015
Beiträge: 64
|
 Khaleb Verfasst am: 06. Jun 2015 18:04 Titel: Als nächstes Khaleb Verfasst am: 06. Jun 2015 18:04 Titel: Als nächstes |
 |
|
|
Als nächstes wollen wir dann einen ausdruck für die in einer feder gespeicherten potentiellen energie finden, als funktion ihrer länge l und mit der ruhelage a und der federkonstante k als parameter also einen formel v = V( l, k, a). Wenn die länge l gleich a ist ist die feder entspannt und v = 0, die potentielle energie steigt mit dem quadrat der differenz der länge von der ruhelänge und zwar mit dem proportionalitätsfaktor k, wie würdest du das in eine formel packen?
|
|
 |
erkü

Anmeldungsdatum: 23.03.2008
Beiträge: 1414
|
|
 |
Khaleb
Anmeldungsdatum: 01.05.2015
Beiträge: 64
|
 Khaleb Verfasst am: 06. Jun 2015 19:11 Titel: Falsch Khaleb Verfasst am: 06. Jun 2015 19:11 Titel: Falsch |
 |
|
Erkü, bei dir sind die federn entspannt und damit ohne gespeicherte energie wenn sie länge null haben, aber laut angabe und wie galvanisfrösche geschrieben hat sollte die energie null sein wenn die federn die länge a haben. Und ausserdem bestimmt x1 nicht direkt eine federlänge. Herumraten ist nicht beispiel lösen. Man muss das auf ganz kleine schritte herunterbrechen und jeden einzelnen davon verstehen. Erst wenn man sehr geübt sit sollte man wenn überhaupt mehrere schritte zusammenfassen.
Zuletzt bearbeitet von Khaleb am 06. Jun 2015 19:20, insgesamt einmal bearbeitet |
|
 |
Khaleb
Anmeldungsdatum: 01.05.2015
Beiträge: 64
|
 Khaleb Verfasst am: 06. Jun 2015 19:19 Titel: Formel für potentielle energie einer feder Khaleb Verfasst am: 06. Jun 2015 19:19 Titel: Formel für potentielle energie einer feder |
 |
|
Also, die potentielle energie einer feder mit federkonstante k und der länge l die bei der länge a entspannt und damit energielos ist lautet = \frac{k}{2} (l-a)^2) wie gewünscht ist die potentielle energie bei l=a genau null. l -a ist was galvanisfrösche oben als x bezeichnet. Jetzt muss man noch den zusammenhang zwischen den längen der beiden federn und x1 sowie x2 finden und dann einsetzen. wie gewünscht ist die potentielle energie bei l=a genau null. l -a ist was galvanisfrösche oben als x bezeichnet. Jetzt muss man noch den zusammenhang zwischen den längen der beiden federn und x1 sowie x2 finden und dann einsetzen.
|
|
 |
erkü

Anmeldungsdatum: 23.03.2008
Beiträge: 1414
|
 erkü Verfasst am: 06. Jun 2015 19:26 Titel: erkü Verfasst am: 06. Jun 2015 19:26 Titel: |
 |
|
@ Khaleb
Die Nulllänge von Federn und sonstige Nulllagen (Ruhelagen) interessieren mich nicht.

Ich konzentriere mich auf die (absoluten) Wechselgrößen !
_________________
Das Drehmoment ist der Moment, wo es zu drehen anfängt. :punk: |
|
 |
Khaleb
Anmeldungsdatum: 01.05.2015
Beiträge: 64
|
 Khaleb Verfasst am: 06. Jun 2015 19:33 Titel: Schön für dich Khaleb Verfasst am: 06. Jun 2015 19:33 Titel: Schön für dich |
 |
|
Ist jetzt nur die frage wieso deine formel dann falsch ist, denn von x1 alleine hängt leider keine federlänge und damit auch kein federpotential ab.
Wenn später was wegfällt schafft das der lagrangeformalismus von ganz alleine.
|
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 06. Jun 2015 19:37 Titel: Re: Schön für dich jh8979 Verfasst am: 06. Jun 2015 19:37 Titel: Re: Schön für dich |
 |
|
| Khaleb hat Folgendes geschrieben: |
Wenn später was wegfällt schafft das der lagrangeformalismus von ganz alleine. |
Oder man definiert sich x1 und x2 von vorneherein als Auslenkung aus der Gleichgewichtslage.. aber wieso einfach wenn es auch kompliziert geht 
|
|
 |
GalvanisFrösche
Anmeldungsdatum: 05.06.2015
Beiträge: 22
|
 GalvanisFrösche Verfasst am: 06. Jun 2015 19:48 Titel: GalvanisFrösche Verfasst am: 06. Jun 2015 19:48 Titel: |
 |
|
| Khaleb hat Folgendes geschrieben: | Also, die potentielle energie einer feder mit federkonstante k und der länge l die bei der länge a entspannt und damit energielos ist lautet = \frac{k}{2} (l-a)^2) wie gewünscht ist die potentielle energie bei l=a genau null. l -a ist was galvanisfrösche oben als x bezeichnet. Jetzt muss man noch den zusammenhang zwischen den längen der beiden federn und x1 sowie x2 finden und dann einsetzen. wie gewünscht ist die potentielle energie bei l=a genau null. l -a ist was galvanisfrösche oben als x bezeichnet. Jetzt muss man noch den zusammenhang zwischen den längen der beiden federn und x1 sowie x2 finden und dann einsetzen. |
Ist das schon die potentielle Energie für beide Federn, also  ? ?
Ich müsste trotzdem  durch ein durch ein 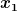 bzw. bzw.  ersetzen, da dies doch die generalisierten Koordinaten sind oder nicht? ersetzen, da dies doch die generalisierten Koordinaten sind oder nicht?
|
|
 |
Khaleb
Anmeldungsdatum: 01.05.2015
Beiträge: 64
|
 Khaleb Verfasst am: 06. Jun 2015 21:36 Titel: Das kommt darauf an was x1 und x2 bedeuten Khaleb Verfasst am: 06. Jun 2015 21:36 Titel: Das kommt darauf an was x1 und x2 bedeuten |
 |
|
Aus der schlampigen zeichnung geht das nicht hervor, da gibts weder koordinatensysteme mit pfeilen, nicht mal eine richtung ob x2 jetzt nach oben oder nach unten gezählt werden soll.Ich interpretiere x2 als die höhe der masse m2 über grund um x1 als die höhe der masse 1 über grund, d.h ich habe ein koordinatensystem wo 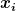 nach oben zeigt und vom boden aus weggezählt wird. Natürlich kann man jederzeit transformieren, d.h. Ich kann auf koordinaten übergehen wo bei nach oben zeigt und vom boden aus weggezählt wird. Natürlich kann man jederzeit transformieren, d.h. Ich kann auf koordinaten übergehen wo bei  vond dort weggezählt wird wo beide federn entspannt sind, also von a und 2a weg, und wieder nach oben positiv. Oder ich kann von den beiden punkten Der gleichgewichtslage wegzählen, wobei die feder zwischnen m2 und boden von beiden massen nach u ten gedrückt wird, und von dort ausgehend die feder zwischen m1 und m2 von der gewichtskraft der masse m1 zusammengepresst. Das sind einfache koordinatentransformationen und als solche ein eigener rechenschritt. Ich bevorzuge zuerst mal die allererste intepratation. vond dort weggezählt wird wo beide federn entspannt sind, also von a und 2a weg, und wieder nach oben positiv. Oder ich kann von den beiden punkten Der gleichgewichtslage wegzählen, wobei die feder zwischnen m2 und boden von beiden massen nach u ten gedrückt wird, und von dort ausgehend die feder zwischen m1 und m2 von der gewichtskraft der masse m1 zusammengepresst. Das sind einfache koordinatentransformationen und als solche ein eigener rechenschritt. Ich bevorzuge zuerst mal die allererste intepratation.
Als gilt für die Feder zwischen m2 und boden l = x2 und ^2) und für die in der feder zwischen m1 und m2 l = x1-x2 und für die gespeicherten energie gilt und für die in der feder zwischen m1 und m2 l = x1-x2 und für die gespeicherten energie gilt^2) . Wie das in der angabe gemeint ist must du allerdings selbst wissen. Die von mir gewählten koordinaten sind halt die höhen über grund und die potentiale sind die tatsächlich in den federn gespeicherten energien und nicht irgendwelche abstrakten rechengrössen. . Wie das in der angabe gemeint ist must du allerdings selbst wissen. Die von mir gewählten koordinaten sind halt die höhen über grund und die potentiale sind die tatsächlich in den federn gespeicherten energien und nicht irgendwelche abstrakten rechengrössen.
|
|
 |
GalvanisFrösche
Anmeldungsdatum: 05.06.2015
Beiträge: 22
|
 GalvanisFrösche Verfasst am: 07. Jun 2015 11:17 Titel: Vorschlag angenommen. GalvanisFrösche Verfasst am: 07. Jun 2015 11:17 Titel: Vorschlag angenommen. |
 |
|
Ok ich nehme deinen Vorschlag an und wähle das KO-System so. Dann habe ich folgende Potentiale:
^2)
^2)


oder ist das zu viel / zu wenig?
Das Gesamtpotential wäre dann
^2 + \frac{k}{2}(x1-x2-a)^2 + 2m g l)
|
|
 |
Khaleb
Anmeldungsdatum: 01.05.2015
Beiträge: 64
|
 Khaleb Verfasst am: 07. Jun 2015 11:56 Titel: Gravitationspotential passt noch nicht Khaleb Verfasst am: 07. Jun 2015 11:56 Titel: Gravitationspotential passt noch nicht |
 |
|
Das gravitationspotential ist, wenn man das gravitationsfeld näherungsweise als konstant auffasst, mgh mit h als höhe über dem bezugsniveau. Als bezugsniveau würde ich wieder den erdboden nehmen, damit wird für masse1 das gravitationspotential 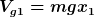 und analog und analog  ,Oder? ,Oder?
Zuletzt bearbeitet von Khaleb am 07. Jun 2015 12:27, insgesamt einmal bearbeitet |
|
 |
GalvanisFrösche
Anmeldungsdatum: 05.06.2015
Beiträge: 22
|
 GalvanisFrösche Verfasst am: 07. Jun 2015 12:26 Titel: Re: Gravitationspotential passt noch nicht GalvanisFrösche Verfasst am: 07. Jun 2015 12:26 Titel: Re: Gravitationspotential passt noch nicht |
 |
|
| Khaleb hat Folgendes geschrieben: | Das gravitationspotential ist, wenn man das gravitationsfeld näherungsweise als konstant auffasst, mgh mit ha als höhe über dem bezugsniveau. Als bezugsniveau würde ich wieder den erdboden nehmen, damit wird für masse1 das gravitationspotential 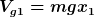 und analog und analog 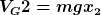 ! Oder? ! Oder? |
Macht Sinn!
Die Lagrangefunktion lautet also
 -\frac{k}{2}(x_2-a)^2 - \frac{k}{2}(x1-x2-a)^2 - m g x_1 - mgx_2)
und dann wären die Bewegungsgleichungen...

=> 
|
|
 |
Khaleb
Anmeldungsdatum: 01.05.2015
Beiträge: 64
|
 Khaleb Verfasst am: 07. Jun 2015 14:21 Titel: Transformationen renormierungen matrizen Khaleb Verfasst am: 07. Jun 2015 14:21 Titel: Transformationen renormierungen matrizen |
 |
|
Jetzt kan man, wenn man lustig ist, noch koordinatentransformationen durchführen, zum beispiel könnte man die 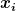 auf die rubelagen beziehen die sich dort befinden wo die beschleunigungen verschwinden. Unter umständen kanmn man auch auf die rubelagen beziehen die sich dort befinden wo die beschleunigungen verschwinden. Unter umständen kanmn man auch  realtiv zu realtiv zu messen mit der länge der feder zwischen m1 und m2 in rubelage als nullpunkt, was dann die formel für die kinetische enrgie ändert. Und man kann die potentiellen energien renormieren indem man konstante terme hinzufügt oder abzählt, wenn sich dadurch etwas vereinfacht. Laut angabe sind ja matrizen der kinetischen und der potentiellen energie gefragt, also matrizen von quadratischen formen der zeitableitungen der koordinaten bzw. Der koordinaten, oder ? messen mit der länge der feder zwischen m1 und m2 in rubelage als nullpunkt, was dann die formel für die kinetische enrgie ändert. Und man kann die potentiellen energien renormieren indem man konstante terme hinzufügt oder abzählt, wenn sich dadurch etwas vereinfacht. Laut angabe sind ja matrizen der kinetischen und der potentiellen energie gefragt, also matrizen von quadratischen formen der zeitableitungen der koordinaten bzw. Der koordinaten, oder ?
|
|
 |
GalvanisFrösche
Anmeldungsdatum: 05.06.2015
Beiträge: 22
|
 GalvanisFrösche Verfasst am: 07. Jun 2015 14:44 Titel: Re: Transformationen renormierungen matrizen GalvanisFrösche Verfasst am: 07. Jun 2015 14:44 Titel: Re: Transformationen renormierungen matrizen |
 |
|
| Khaleb hat Folgendes geschrieben: | | Laut angabe sind ja matrizen der kinetischen und der potentiellen energie gefragt, also matrizen von quadratischen formen der zeitableitungen der koordinaten bzw. Der koordinaten, oder ? |
Ja genau.
Als Matrix wäre dies dann so
 für für



wenn ich mich nicht täusche...
Leider ist der Ausdruck etwas unglücklich wegen -ak und mg aber ist halt so...
|
|
 |
Khaleb
Anmeldungsdatum: 01.05.2015
Beiträge: 64
|
 Khaleb Verfasst am: 07. Jun 2015 15:40 Titel: Das sind zwar matrizen Khaleb Verfasst am: 07. Jun 2015 15:40 Titel: Das sind zwar matrizen |
 |
|
Also du hast jetzt zwar die bewegungsgleichungen in matrixform aufgeschrieben, aber als matrizen der kinetischen energie und der potentiellen energie hätte ich mir etwas erwartet wie  und und  erwartet, oder? erwartet, oder?  (konstanten in der potentiellen energie kann man durch renormierung wegbringen) (konstanten in der potentiellen energie kann man durch renormierung wegbringen)
|
|
 |
GalvanisFrösche
Anmeldungsdatum: 05.06.2015
Beiträge: 22
|
 GalvanisFrösche Verfasst am: 07. Jun 2015 15:58 Titel: Re: Das sind zwar matrizen GalvanisFrösche Verfasst am: 07. Jun 2015 15:58 Titel: Re: Das sind zwar matrizen |
 |
|
| Khaleb hat Folgendes geschrieben: | Also du hast jetzt zwar die bewegungsgleichungen in matrixform aufgeschrieben, aber als matrizen der kinetischen energie und der potentiellen energie hätte ich mir etwas erwartet wie  und und  erwartet, oder? erwartet, oder?  (konstanten in der potentiellen energie kann man durch renormierung wegbringen) (konstanten in der potentiellen energie kann man durch renormierung wegbringen) |
Meins ist eine äquivalente Schreibweise weil doch:

in der Lagrangefunktion geschrieben werden kann als:

wobei die  und und  Matrizen sind. Matrizen sind.
Aber wie würdest du es denn aufschreiben, wenn nicht so ? - Man soll ja eine allgemeine Lösung finden und in meiner Schreibweise, könnte man dann als allgemeine Lösung:
 )
und als spezielle Lösung irgendwas wie -ak + mg oder so nehmen...
k.a.  Ich glaube das geht Ich glaube das geht 
|
|
 |
Khaleb
Anmeldungsdatum: 01.05.2015
Beiträge: 64
|
 Khaleb Verfasst am: 07. Jun 2015 16:33 Titel: Eine Lösung finden ist auch gefragt? Khaleb Verfasst am: 07. Jun 2015 16:33 Titel: Eine Lösung finden ist auch gefragt? |
 |
|
Ich seh in deinem ersten posting nicht dass man die gleichungen auch lösen soll, da steht nur dass man die matrizen der energien bestimmen soll. Ich denke die glieder erster ordnung in der potentiellen energie meiner formel (die  ) bekommt man mit einer transformation ) bekommt man mit einer transformation  weg( in der kinetischen energie ändert sich dadurch nix weil die konstanten weg( in der kinetischen energie ändert sich dadurch nix weil die konstanten  bei der zeitableitung rausfallen), und die entstehenden neuen konstanten glieder eliminiert man wieder mit einer renormierung der potentiellen energie weg ( in dem man sie einfach weglässt), würd mich interessieren was da rauskommt. Also man setzt die bei der zeitableitung rausfallen), und die entstehenden neuen konstanten glieder eliminiert man wieder mit einer renormierung der potentiellen energie weg ( in dem man sie einfach weglässt), würd mich interessieren was da rauskommt. Also man setzt die  als unbekannte an und bestimmt sie so dass die linearen glieder in den als unbekannte an und bestimmt sie so dass die linearen glieder in den 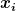 wegfallen. wegfallen.
|
|
 |
GalvanisFrösche
Anmeldungsdatum: 05.06.2015
Beiträge: 22
|
 GalvanisFrösche Verfasst am: 07. Jun 2015 17:04 Titel: Re: Eine Lösung finden ist auch gefragt? GalvanisFrösche Verfasst am: 07. Jun 2015 17:04 Titel: Re: Eine Lösung finden ist auch gefragt? |
 |
|
| Khaleb hat Folgendes geschrieben: | | Ich seh in deinem ersten posting nicht dass man die gleichungen auch lösen soll, da steht nur dass man die matrizen der energien bestimmen soll. |
Stimmt! Habs irgendwie durcheinander gebracht..
Ok dann habe ich das so gemacht und erhalte:
 - k(x_2 - x_{20}) - ak + mg&=& 0 \\
<br />
m \ddot{x}_2 +2k(x_2 - x_{20}) - k(x_1 - x_{10})+mg&=& 0 )
Aber was vereinfacht sich dadurch?
|
|
 |
Khaleb
Anmeldungsdatum: 01.05.2015
Beiträge: 64
|
 Khaleb Verfasst am: 07. Jun 2015 17:44 Titel: Die potentielle enenergie soll sich vereinfachen Khaleb Verfasst am: 07. Jun 2015 17:44 Titel: Die potentielle enenergie soll sich vereinfachen |
 |
|
Galvanisfrosch, die potentielle energie soll sich vereinfachen zu  also nur produkte von also nur produkte von  enthalten und keine terme mit enthalten und keine terme mit 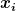 alleine durch die koordinatenverschiebung. Rauskommen sollte meiner meinung nach dass du in die gleichgewichtslagen verschieben musst, denk ich. alleine durch die koordinatenverschiebung. Rauskommen sollte meiner meinung nach dass du in die gleichgewichtslagen verschieben musst, denk ich.  (und in den bewegungsgleichungen haben dir doch diese konstanten terme Irgendwie nicht gefallen, oder?) (und in den bewegungsgleichungen haben dir doch diese konstanten terme Irgendwie nicht gefallen, oder?)
|
|
 |
GalvanisFrösche
Anmeldungsdatum: 05.06.2015
Beiträge: 22
|
 GalvanisFrösche Verfasst am: 07. Jun 2015 18:22 Titel: Re: Die potentielle enenergie soll sich vereinfachen GalvanisFrösche Verfasst am: 07. Jun 2015 18:22 Titel: Re: Die potentielle enenergie soll sich vereinfachen |
 |
|
| Khaleb hat Folgendes geschrieben: | Galvanisfrosch, die potentielle energie soll sich vereinfachen zu  also nur produkte von also nur produkte von  enthalten und keine terme mit enthalten und keine terme mit 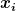 alleine durch die koordinatenverschiebung. Rauskommen sollte meiner meinung nach dass du in die gleichgewichtslagen verschieben musst, denk ich. alleine durch die koordinatenverschiebung. Rauskommen sollte meiner meinung nach dass du in die gleichgewichtslagen verschieben musst, denk ich.  (und in den bewegungsgleichungen haben dir doch diese konstanten terme Irgendwie nicht gefallen, oder?) (und in den bewegungsgleichungen haben dir doch diese konstanten terme Irgendwie nicht gefallen, oder?) |
Ich verstehe leider nicht was du meinst 
Wo soll ich jetzt was ersetzen. Soll ich in die potentielle Energie dies  einsetzen oder was soll ich tun? einsetzen oder was soll ich tun?
|
|
 |
Khaleb
Anmeldungsdatum: 01.05.2015
Beiträge: 64
|
 Khaleb Verfasst am: 07. Jun 2015 18:41 Titel: Genau Khaleb Verfasst am: 07. Jun 2015 18:41 Titel: Genau |
 |
|
Du setzt in der Formel für die potentiell energie  ein und bestimmts die ein und bestimmts die  dann so dass die linearen glieder in den dann so dass die linearen glieder in den  verschwinden. verschwinden.
|
|
 |
GalvanisFrösche
Anmeldungsdatum: 05.06.2015
Beiträge: 22
|
 GalvanisFrösche Verfasst am: 07. Jun 2015 18:58 Titel: Re: Genau GalvanisFrösche Verfasst am: 07. Jun 2015 18:58 Titel: Re: Genau |
 |
|
| Khaleb hat Folgendes geschrieben: | Du setzt in der Formel für die potentiell energie  ein und bestimmts die ein und bestimmts die  dann so dass die linearen glieder in den dann so dass die linearen glieder in den  verschwinden. verschwinden. |
^2 + \frac{k}{2}(\bar{x_1} - x_{10}-\bar{x}_2- - x_{20} - a)^2 + m g x_1 + mgx_2)
dann kann man noch ausmultiplizieren...aber das wird nur unschön:
+ mg (\bar{x}_1 + x_{10}) + mg ( \bar{x}_2 + x_{20}))
wenn ich nichts falsch gemacht hab..Vielleicht geht das eleganter mit Summationszeichen
Ich bin immer noch ratlos was dann zu tun ist..?
|
|
 |
Khaleb
Anmeldungsdatum: 01.05.2015
Beiträge: 64
|
 Khaleb Verfasst am: 07. Jun 2015 21:00 Titel: Jetzt hast du 2 möglichkeiten Khaleb Verfasst am: 07. Jun 2015 21:00 Titel: Jetzt hast du 2 möglichkeiten |
 |
|
Also, in beiden möglichkeiten streichts du In deiner formel für V zuerst alle terme die konstant sind, also nicht von und und  abhängen. Deine begründung dafüri ist: ich renormiere die potentielle energie um einen konstanten wert, eben die summe aller eben gestrichenen terme. abhängen. Deine begründung dafüri ist: ich renormiere die potentielle energie um einen konstanten wert, eben die summe aller eben gestrichenen terme.
Dann kommt möglichkeit 1: du bist an den konkreten werten der  interessiert. Dann musst du zuerst die summe der terme die nur interessiert. Dann musst du zuerst die summe der terme die nur  in der ersten potenz haben herausnehmen (koeffizientenvergleich) und null setzen und bekommst die erste gleichung für die in der ersten potenz haben herausnehmen (koeffizientenvergleich) und null setzen und bekommst die erste gleichung für die  . das selbe machst du mit den termen die nur . das selbe machst du mit den termen die nur  in der ersten potenz enthalten und bekommst die 2.gleichung. Dieses lineare gleichungssystem löst du und bekommst die beiden in der ersten potenz enthalten und bekommst die 2.gleichung. Dieses lineare gleichungssystem löst du und bekommst die beiden  . Jetzt hast du die komplette punkttransformation. Die potentielle energie mit diesen werten hat dann keine linearen terme in . Jetzt hast du die komplette punkttransformation. Die potentielle energie mit diesen werten hat dann keine linearen terme in  . Wenn du die werte für . Wenn du die werte für  in die ursprüngliche bewegungsgleichung einsetzt solltest du sehen dass an dieser stelle die beschleunigung verschwindet und du genau auf die gleichgewichtslage transformiert hast. in die ursprüngliche bewegungsgleichung einsetzt solltest du sehen dass an dieser stelle die beschleunigung verschwindet und du genau auf die gleichgewichtslage transformiert hast.
Möglichkeit 2 ist die faule: du bist an den konkreten werten der  nicht interessiert. Du nimmst an das sich ergebende gleichungssystem für die nicht interessiert. Du nimmst an das sich ergebende gleichungssystem für die  von oben sei lösbar und du hättest die werte ausgerechnet und streichst mit dieser begründung die terme die linear in von oben sei lösbar und du hättest die werte ausgerechnet und streichst mit dieser begründung die terme die linear in  sind weil die sind weil die  ja genau das null werden der summe dieser terme bewirken. ja genau das null werden der summe dieser terme bewirken.
Jedenfalls sieht dann die potentielle enenergie folgendermassen aus (genau deine obige formel nur sind die konstanten und die in  linearen terme gestrichen): linearen terme gestrichen):
=\frac{k}{2}(\bar{x_1}-\bar{x_2})^2 +\frac{k}{2}\bar{x_2}^2 ) schaut doch gleich viel einfacher aus, nicht? Wenn du damit die bewegungsgleichungen bildest siehts du dass bei schaut doch gleich viel einfacher aus, nicht? Wenn du damit die bewegungsgleichungen bildest siehts du dass bei  die beschleunigung verschwindet und das daher die gleichgewichtslage ist. Ah ja, und Diese formel der potentiellen energie musst du noch in matrixform bringen. die beschleunigung verschwindet und das daher die gleichgewichtslage ist. Ah ja, und Diese formel der potentiellen energie musst du noch in matrixform bringen.
|
|
 |
GalvanisFrösche
Anmeldungsdatum: 05.06.2015
Beiträge: 22
|
 GalvanisFrösche Verfasst am: 08. Jun 2015 09:00 Titel: GalvanisFrösche Verfasst am: 08. Jun 2015 09:00 Titel: |
 |
|
|
Gut Danke dann kam man tatsächlich auf die oben erwähnte Bewegungsgleichung
|
|
 |
|



















 ok, jetzt sehe ich den Fehler !
ok, jetzt sehe ich den Fehler !