| Autor |
Nachricht |
seeker2208
Gast
|
 seeker2208 Verfasst am: 22. Aug 2015 11:55 Titel: Unterschied 'proper time' zu 'conformal time' seeker2208 Verfasst am: 22. Aug 2015 11:55 Titel: Unterschied 'proper time' zu 'conformal time' |
 |
|
Hallo,
wie ist bitte die "conformal time" zu verstehen, im Unterschied zur "proper time", die seit dem Bigbang in FRW-Modellen verstrichen ist ?
Proper time --> ca. 13,7 Gyr, conformal time --> ca. 46 Gyr, distance to particle horizon --> ca. 46 Gly.
Ist die conformal time soetwas wie eine "gedehnte" proper time ?
thx
seeker |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 22. Aug 2015 15:54 Titel: index_razor Verfasst am: 22. Aug 2015 15:54 Titel: |
 |
|
Die FRW-Metrik ist konform flach, also von der Form
(c^2\dd t^2 - \dd r^2).)
Ist nur eine Vermutung, aber möglicherweise ist  hier mit "comformal time" gemeint. Das paßt, denke ich, zum particle horizon den du erwähnst, denn da lichtartige Trajektorien hier mit "comformal time" gemeint. Das paßt, denke ich, zum particle horizon den du erwähnst, denn da lichtartige Trajektorien 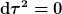 vom Skalenfaktor vom Skalenfaktor ) nichts mitbekommen, ist der maximale mitbewegte Abstand nichts mitbekommen, ist der maximale mitbewegte Abstand  , den ein Teilchen seit dem Urknall im FRW-Universum zurückgelegt haben kann, gleich , den ein Teilchen seit dem Urknall im FRW-Universum zurückgelegt haben kann, gleich 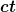 : :

PS: Die Vermutung scheint zu stimmen
https://en.wikipedia.org/wiki/Particle_horizon#Conformal_time_and_the_particle_horizon |
|
 |
seeker2208
Gast
|
 seeker2208 Verfasst am: 22. Aug 2015 16:15 Titel: seeker2208 Verfasst am: 22. Aug 2015 16:15 Titel: |
 |
|
Danke Dir, das hat mir sehr geholfen es zu verstehen.
Gruß,
seeker |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 23. Aug 2015 09:29 Titel: TomS Verfasst am: 23. Aug 2015 09:29 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | Die FRW-Metrik ist konform flach, also von der Form
(c^2\dd t^2 - \dd r^2).) |
Man kann die FRW-Metrik in dieser Form angeben, aber das ist nicht die übliche Form.
Normalerweise setzt man
 \, (\dd r^2 + r^2 \, \dd \Omega))
Dabei handelt es sich um comoving coordinates, d.h. bei t um die comoving time. Diese entspricht der proper time mitbewegter Beobachter, denn für
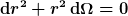
ist
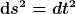
Nun kann man die conformal time eta mittels
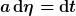
und der Metrik
 \, [\dd \eta^2 - (\dd r^2 + r^2 \, \dd \Omega)])
einführen.
Was ist der Unterschied? Betrachten wir radiale Lichtstrahlen, also
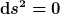

In comoving coordinates gilt
 \, \dd r^2 = 0)

In conformal time gilt


D.h. in comoving coordinates liefert die Ableitung nicht die Lichtgeschwindigkeit. Nun ist die Zeitkoordinate tatsächlich die proper time mitbewegter Beobachter, jedoch liefert die Ortskoordinate nicht die proper distance (außer für mitbewegte Beobachter).
Zuletzt bearbeitet von TomS am 24. Aug 2015 13:12, insgesamt einmal bearbeitet |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 23. Aug 2015 12:17 Titel: index_razor Verfasst am: 23. Aug 2015 12:17 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | Die FRW-Metrik ist konform flach, also von der Form
(c^2\dd t^2 - \dd r^2).) |
Man kann die FRW-Metrik in dieser Form angeben, aber das ist nicht die übliche Form.
|
Das mag ja sein. Es ist aber die Form, in der die Koordinate t der konformen Zeit entspricht und man erkennt was das ganze überhaupt mit "konform" zu tun hat. Ich sehe in deiner Erklärung auch keinen Unterschied zu meiner mit Ausnahme der Bezeichnungen. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 23. Aug 2015 23:10 Titel: TomS Verfasst am: 23. Aug 2015 23:10 Titel: |
 |
|
Meine Erklärung ist etwas ausführlicher ;-)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
seeker2208
Gast
|
 seeker2208 Verfasst am: 24. Aug 2015 11:49 Titel: seeker2208 Verfasst am: 24. Aug 2015 11:49 Titel: |
 |
|
Danke für den Nachtrag. Folgefrage:
Der particle horizon wird mit 46 Gly angegeben, was nach meinem Vertständnis die max. Entfernung angibt, die ein Lichtsignal in Eigenbewegung inkl. der Raumausdehnung erreichen kann.
Wie groß ist dann die maximale Ausdehnung nur des Raums selbst ?
thx !
seeker |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 24. Aug 2015 15:02 Titel: TomS Verfasst am: 24. Aug 2015 15:02 Titel: |
 |
|
Was meinst du mit "maximale Ausdehnung des Raumes selbst"?
Zunächst mal müssen wir verschiedene Entfernungsbegriffe unterscheiden.
Für einen "Schnappschuss" zu fester Zeit t folgt die proper distance als die Entfernung, die für diese feste Zeit t auf einem Maßstab abgelesen werden könnte. Für feste Zeit t gilt
 \, \dd r)
und damit der radiale Abstand zweier Ereignisse mit Koordinaten (t,0) und (t,r) als
 = a(t) \, r)
Diese beiden Ereignisse sind raumartig.
Für lichtartige Ereignisse setzen wir dagegen
 \, \dd r)
und erhalten durch Integration die comoving distance entlang des Vergangenheitslichtkegels
 = \int_{t_\text{em}}^{t_\text{obs}} \frac{\dd t}{a(t)})
Der particle horizon entspricht der maximalen comoving distance, von der aus ein hypothetisches Photon, das zum Zeitpunkt des Urknalls t = 0 emittiert wurde, uns gerade jetzt erreicht:
 = \int^{t_\text{now}}_0 \frac{\dd t}{a(t)})
Wenn du von "maximaler Ausdehung des Raumes selbst" sprichst, dann musst du zunächst mal den verwendeten Entfernungsbegriff angeben. Als nächstes musst du du dich auf ein bestimmtes Modell des Universums festlegen, d.h. eine konkrete Zeitabhängigkeit des Skalenfaktors a(t) angeben (FRW wird vorausgesetzt). Damit werden die Entfernungen berechenbar.
Beachte, dass das Integral für physikalische Skalenfaktoren endlich ist, d.h. der particle horizon hat eine endliche Entfernung, selbst wenn die proper distance in einem unendlichen Universum für beliebig kleine Zeiten t unbeschränkt ist (da r unbeschränkt ist). Ein solches Universum war also schon immer unendlich groß, auch wenn das sichtbar Universum endliche Größe hat.
Zuletzt kann man noch überlegen, ob das Universum einen event horizon enthält, ob also in unendlich ferner Zukunft ein Sichtbarkeitshorizont existiert. Dieser folgt - falls das Integral existiert - gemäß
 = \int_{t_\text{em}}^\infty \frac{\dd t}{a(t)})
Auch in diesem Fall ist nur das sichtbare Universum endlich. |
|
 |
seeker2208
Gast
|
 seeker2208 Verfasst am: 24. Aug 2015 16:12 Titel: seeker2208 Verfasst am: 24. Aug 2015 16:12 Titel: |
 |
|
Danke Dir für Deine sehr ausführliche Antwort. Ich muß diese nochmal auf mich wirken lassen.
Ich dachte irgendwie, daß in dem Betrag für den particle horizon 46 Gly die max. Ausdehnung des Raums implizit gegeben ist, wenn ich die Photonenbewegung quasi rausrechne a la "die 46 Gly entsprechen 30 Gly Raumausdehnung und 16 Gly Photonenbewegung".
Gruß,
seeker |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 24. Aug 2015 18:00 Titel: TomS Verfasst am: 24. Aug 2015 18:00 Titel: |
 |
|
Du kannst da nicht so einfach etwas rausrechnen bzw. eine Addition vornehmen; das geht zufälligerweise bei der proper distance, die als Produkt darstellbar ist - s.o., nicht jedoch bei der commoving distance und ihrer Integraldarstellung.
Schau dir doch mal einen FAQ-Beitrag an
http://www.physikerboard.de/topic,43356,-faq---kosmologische-expansion---ameise-auf-einem-gummiband.html
Das Gummiband kann doch unendlich sein, auch wenn wir nur endliche Zeiten und endliche Abschnitte auf dem Band betrachten. Es ist trivial, dass innerhalb endlicher Zeit nur endliche Distanzen zurückgelegt werden können.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
seeker2208
Gast
|
 seeker2208 Verfasst am: 24. Aug 2015 18:58 Titel: seeker2208 Verfasst am: 24. Aug 2015 18:58 Titel: |
 |
|
ok danke, da hast Du natürlich recht.
Gruß,
seeker
ps: der Beitrag mit der Ameise bei den FAQ ist wirklich gut ... |
|
 |
seeker2208
Gast
|
 seeker2208 Verfasst am: 25. Aug 2015 14:38 Titel: seeker2208 Verfasst am: 25. Aug 2015 14:38 Titel: |
 |
|
kleine Verständnisfrage noch. In der Formel für den partikelhorizont, wie komme ich da auf die 46 Glyr ? Rechts im bestimmten Integral steht doch 1 dt/ a(t0) also dt/1. Und bei Integrationsgrenzen von 0 bis 13,5 Gyr bekomme ich dann c * 13,5 Gyr also 13,5 Glyr. Stehe auf dem Schlauch ...
thx !
seeker |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 25. Aug 2015 15:33 Titel: TomS Verfasst am: 25. Aug 2015 15:33 Titel: |
 |
|
Unter Integral steht dt/a(t), d.h. du musst ein konkretes a(t) einsetzen und integrieren. Dazu findest du im Internet viele Quellen.
Beachte, dass der Teilchenhorizont meist ebenfalls als proper distance
 \, \chi_\text{ph}(t_\text{now}) = a(t_\text{now}) \, \int^{t_\text{now}}_0 \frac{\dd t}{a(t)})
anstelle der comoving distance
 = \int^{t_\text{now}}_0 \frac{\dd t}{a(t)})
angegeben wird.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
seeker2208
Gast
|
 seeker2208 Verfasst am: 25. Aug 2015 21:38 Titel: seeker2208 Verfasst am: 25. Aug 2015 21:38 Titel: |
 |
|
Danke nochmals für Deine ausführliche Erklärung. Habe auch oben meinen Denkfehler (post davor) gefunden, ich muß ja die conformal time nehmen und nicht das weltalter.
Abschlußfrage: Wenn ich recht verstehe, dann gilt die Fluchtgeschwindigkeit, die über die Hubblekonstante definiert ist, in comoving distance. Wenn ich nun ausrechnen möchte, welche Entfernung eine Galaxie, die heute zu t_0 eine Entfernung in comoving distance von z.b. 10 Glyr aufweist (die ich also in 10 Glyr Entfernung "sehe"), in Wirklichkeit in proper distance hat, wie muß ich da vorgehen ?
thx !
seeker |
|
 |
seeker2208
Gast
|
 seeker2208 Verfasst am: 26. Aug 2015 12:05 Titel: seeker2208 Verfasst am: 26. Aug 2015 12:05 Titel: |
 |
|
Hi Tom,
ich bin jetzt maximal verwirrt. Im Wiki-Artikel über "Entfernungsmaß" ist es genau andersrum erklärt, oder ich verstehe es falsch. Dort wird die Laufzeitentfernung mit der proper distance gleichgesetzt und die comoving distance mit Ereignissen, die zu konstanter kosmologischer Zeit t0 stattfinden, also raumartig sind.
Zitat:
"Laufzeitentfernung ist die die Distanz zu dem Objekt, so wie der Beobachter es sieht, und dieser sieht es in einem Zustand der vergangenheit..."
also entlang des Lichtkegels.
verwirrt,
seeker |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 26. Aug 2015 18:42 Titel: TomS Verfasst am: 26. Aug 2015 18:42 Titel: |
 |
|
Englische Wikipedia zu light-travel distance
"This [light-travel] distance is the time ... that it took light to reach the observer from the object multiplied by the speed of light. For instance, the radius of the observable universe in this distance measure becomes the age of the universe multiplied by the speed of light ... i.e. 13.8 billion light years."
Die light travel distance = Lichtlaufzeitdistanz ist also eine gedachte Distanz, jedoch tatsächlich eine Zeit!

Man beachte, dass die Zeitkoordinate t entlang des Lichtkegels nicht konstant ist, d.h. es handelt sich insbs. nicht um die proper distance (s.o.)
Die Lichtlaufzeit für ein Objekt, das wir heute sehen, ist maximal so groß wie das Universum alt ist, denn länger kann das Licht ja nicht unterwegs sein. Die proper distance = Eigendistanz desselben Objektes heute entspricht jedoch der Entfernung des Objektes gemessen in einem Schnappschuss heute für t = const. Die proper distance = Eigendistanz desselben Objektes kann also in einem expandierenden Universum beliebig größer sein als die light travel distance = Lichtlaufzeitdistanz.
Betrachte ein Objekt, das sich kurz nach dem Urknall gebildet hat, und das du heute siehst.
Du selbst hast heute die Koordinaten
)
und sitzt also (in deinem Koordinatensystem) im Zentrum.
1) Das Objekt hatte zum Zeitpunkt seiner Entstehung die Koordinaten
)
2) Das Objekt hat "heute" (= dein heute extrapoliert durch eine raumartige Geodäte von dir heute zum Objekt) die Koordinaten
))
wobei der zeitabhängige Radialkoordinate andeuten soll, dass sich das Objekt aufgrund der Expansion des Universums mit diesem mit- und somit von dir fortbewegt hat.
(1) liegt also in der Vergangenheit von (2)
1) Die light-travel distance = Lichtlaufzeitdistanz misst nun den lichtartigen Abstand von dir heute zum Ereignis der Entstehung des Objektes entlang des Lichtkegels "rückwärts" in der Zeit t.
2) Die proper distance = Eigendistanz misst den räumlichen Abstand von dir heute zu einem raumartigen und insbs. gleichzeitigen Ereignis am Ort des Objektes.
Wenn du das nun auf dich selbst anwendest, d.h. wenn du annimmst, dass du selbst zum Zeitpunkt des Urknalls entstanden bist, dann entspricht deine heutige Lichtlaufzeitdistanz zum Ereignis deiner Entstehung exakt deiner Eigenzeit = exakt deinem jetzigen Alter = exakt dem jeweiligen Alter des Universums. Deine Eigendistanz zu dir selbst ist jedoch sicher zu jedem Zeitpunkt exakt Null, da du für eine beliebige aber feste Eigenzeit von dir selbst immer den Abstand Null hast. |
|
 |
seeker2208
Gast
|
 seeker2208 Verfasst am: 27. Aug 2015 09:35 Titel: seeker2208 Verfasst am: 27. Aug 2015 09:35 Titel: |
 |
|
Danke nochmals Tom für die Zeit die Du aufwendest, mir das Thema näherzubringen. Ich muß da noch etwas nacharbeiten und will Deine Zeit nicht übermaß beanspruchen, deshalb nur noch kurz die Punkte:
1. Die Unterschiede habe ich denke ich grob Verstanden, einzig bei der Abgrenzung comoving distance zu proper distance hapert es noch. Ist dies dasselbe ? Man findet mitunter dieselben Formeln in papern, aber einmal mit Bezeichnung D_prop und einmal mit D_com
2. Die Hubblekonstante mit der Angabe von z.B. v_rec = 70 km/s pro Mpc und v_rec(0) = D(0) H(0) ist die Entfernung D die proper Distance, richtig ? Im Folgeschluß ist der Hubbleradius die Entfernung gemessen auf der raumartigen Hyperfläche zur allg. kosmologischen Zeit t_0 und nicht gemessen auf dem Vergangenheitslichtkegel, richtig ?
Danke nochmal für kurze Beantwortung,
Gruß,
seeker |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 27. Aug 2015 13:57 Titel: TomS Verfasst am: 27. Aug 2015 13:57 Titel: |
 |
|
| seeker2208 hat Folgendes geschrieben: | | 1. Die Unterschiede habe ich denke ich grob Verstanden, einzig bei der Abgrenzung comoving distance zu proper distance hapert es noch. Ist dies dasselbe ? Man findet mitunter dieselben Formeln in papern, aber einmal mit Bezeichnung D_prop und einmal mit D_com |
Habe ich in meinem Beitrag vom 24. Aug., 15:02 zusammengefasstM; das sind die Definitionen, die ich kenne; schlimmstenfalls gibt es davon abweichende
| seeker2208 hat Folgendes geschrieben: | | 2. Die Hubblekonstante mit der Angabe von z.B. v_rec = 70 km/s pro Mpc und v_rec(0) = D(0) H(0) ist die Entfernung D die proper Distance, richtig ? Im Folgeschluß ist der Hubbleradius die Entfernung gemessen auf der raumartigen Hyperfläche zur allg. kosmologischen Zeit t_0 und nicht gemessen auf dem Vergangenheitslichtkegel, richtig ? |
Ja, ich denke, du hast das richtig verstanden.
Zunächst mal definieren wir
 = \frac{\dot{a}(t)}{a(t)})
 = H(t)\,D_\text{prop}(t))
Früher hatten wir schon
 = a(t) \, r)
Daraus folgt
 = \frac{\dot{a}(t)}{a(t)}\,a(t) \, r = \dot{a}(t) \, r)
Wikipedia: "... the Hubble sphere is a spherical region ... surrounding an observer beyond which objects recede from that observer at a rate greater than the speed of light ... The proper radius of a Hubble sphere (known as the Hubble radius or the Hubble length) is c/H ..."
Da hier immer "proper" length, radius, ... sowie die konstante Zeit t verwendet wird, liegt wiederum eine proper distance vor:
 = \frac{v_\text{rec}(t)}{H(t)})
 = D_\text{prop}(t)|_{v_\text{rec} = 1} = \frac{1}{H(t)} )
D.h. Objekte auf der "gleichzeitigen Hubblesphäre" haben diese entsprechende proper distance.
Die Koordinaten des Beobachters sowie der Hubblesphäre sind
)
, t))
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 27. Aug 2015 14:00 Titel: TomS Verfasst am: 27. Aug 2015 14:00 Titel: |
 |
|
Anmerkung: Die Hubblesphäre definiert i.A. keinen Horizont. Auch ist die Rezessionsgeschwindigkeit = c eine künstliche, nicht-lokale Geschwindigkeitsdefinition; c stellt nur bzgl. lokal definierter bzw. gemessener Relativgeschwindigkeit eine Obergrenze dar.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
seeker2208
Gast
|
 seeker2208 Verfasst am: 27. Aug 2015 14:31 Titel: seeker2208 Verfasst am: 27. Aug 2015 14:31 Titel: |
 |
|
prima, dann komme ich glaube ich in diesem Thema erstmal zurecht.
Vielen Dank nochmals,
Seeker |
|
 |
seeker_2208
Gast
|
 seeker_2208 Verfasst am: 14. Sep 2015 13:03 Titel: seeker_2208 Verfasst am: 14. Sep 2015 13:03 Titel: |
 |
|
Habe nochmal eine Verständnisfrage zur FRW-Metrik
 \, (\dd r^2 + x^2 \, \dd \Omega))
und den Darstellungen für einen flachen, sphärischen und hyperbolischen Raum.
für "flach" ist x = r
für sphärisch ist
))
Wenn man das nun so in einem D2-Koordinatensystem darstellt, daß sich jeweils a) eine senkrechte Linie, b) ein Kreisbogen und c) eine Hyperbel vom Koordinatenursprung entlang der x-Achse wegbewegen, daß je größer der Abstand zum 0-Punkt wird, die Ausdehnung von a, b oder c auch immer größer wird, dann stellt sich mir die Frage:
Ist eine flache bzw. eine hyperbolische Raumzeit überhaupt physikalisch möglich ?
Das Koordinatensystem stellt nun eine 4D-Raumzeit dar, wobei a, b oder c den Schnitt durch die Raumzeit (=Raum) repräsentiert, die Bewegung entlang der x-Achse den Zeitverlauf.
Wenn dies so zulässig ist, dann würde doch ein flacher Raum und ein hyperbolischer Raum bedeuten, daß sich jeder Punkt des Raums mit unterschiedlichen "Geschwindigkeiten" durch die Raumzeit
bewegen, nur bei sphärischen Raum wären alle Punkte der Raumzeit gleich schnell (Geschwindigkeit setzte ich hier gleich mit der Länge eines Vektors vom Koordinatenursprung zu einem beliebigen Raumpunkt.)
Im Falle der flachen Raumzeit müßten demnach diese "Einzelgeschwindigkeiten der Raumpunkte" so fein abgestimmt
sein, daß es überhaupt dazu kommt, daß sich eine "Gerade" durch die Raumzeit bewegt. Wäre das nicht so, als würde man beim Werfen eines Steins in Wasser erwarten, daß sich keine Kreiswellen bilden
sondern eine flache Wellenfront ?
Danke für Einschätzungen,
seeker |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 14. Sep 2015 17:20 Titel: TomS Verfasst am: 14. Sep 2015 17:20 Titel: |
 |
|
Was meinst du mit "Geschwindigkeit der Raumpunkte"? In welchen Koordinaten betrachtest du diese?
Was du mit den Koordinstensystemen und (a - c) bezweckst, verstehe ich nicht. Kannst du mal eine Zeichnung machen? |
|
 |
seeker_2208
Gast
|
 seeker_2208 Verfasst am: 14. Sep 2015 17:28 Titel: seeker_2208 Verfasst am: 14. Sep 2015 17:28 Titel: |
 |
|
ja, mache ich, wird aber wohl erst morgen,
Gruß,
seeker |
|
 |
seeker_2208
Gast
|
 seeker_2208 Verfasst am: 15. Sep 2015 15:11 Titel: seeker_2208 Verfasst am: 15. Sep 2015 15:11 Titel: |
 |
|
Schaffe das vor heute abend nicht mit der Zeichnung, vielleicht gehts vorab auch verblich anhand Expansion eines konstant flachen Universums.
1. Normales x-y-Koordinatensystem mit Zeitentwicklung +t entlang der positiven x-Achse und zunehmender Raumausdehnung des modellhaften Universums auf der positiven und negativen y-Achse
2. Das flache Universum zum heutigen Zeitpunkt mit heutiger Ausdehnung sei durch eine Senkrechte zur x-Achse dargestellt, die vom Punkt (3,3) zum Punkt (3,-3) verläuft. Die Senkrechte ist quasi ein Schnitt durch die Raumzeit.
3. Das Universum hatte beim Punkt (0,0) einen kompakten Anfang.
4. Wenn ich vom Punkt (0,0) jeweils eine Gerade zu den Enden der Senkrechten ziehe, dann ergibt diese Fläche (Dreieck) die Weltfläche des flachen Universums über die Zeit betrachtet. Das Universum hat sich über die Zeit kontinuierlich ausgedehnt, deshalb ist die Senkrechte immer länger geworden.
Jetzt folgende Überlegung:
Die Fläche des Dreiecks sei modellhaft die Raumzeit (R^3 x Zeit), die Senkrechte zu einem beliebigen Zeitpunkt t ein Schnitt durch die Raumzeit.
Wenn man sich jetzt Gedanken über die Rate (Geschwindigkeit passt hier denke ich nicht) macht mit der die Senkrechte sich entlang der x-Achse bewegt hat dann kann man ja versuchen dies mit Vektoren darzustellen, die vom Koordinatenursprung (0,0) zu einem beliebigen Punkt der Senkrechten gehen. Die Vektoren sollen Auskunft über die Rate geben, mit der sich jeder einzelne Punkt der Senkrechten "durch die Zeit" bewegt. Dabei wird man feststellen, daß ein Vektor umso länger ist, je weiter sich der Punkt auf der Senkrechten von der x-Achse entfernt befindet. Wenn man die Vektorläge z.B. als Geschwindigkeit deuten würde, dann hieße das, daß sich alle Punkte auf der Geraden (die den flachen Raum darstellt) mit unterschiedlicher "Geschwindigkeit" durch die Zeit bewegen.
Ich frage mich, ob dies überhaupt möglich ist, daß ein flacher Raum (Schnitt durch die Raumzeit) einen kompakten Anfang haben kann und sich über die Zeit so entwickelt, daß er "wie ein Brett" durch die Raumzeit fliegt. Selbige Frage stellt sich mir bei einem hyperbolischen Unibversum. Nur bei einem sphärischen Universum würden sich alle Punkte des Raums mit selber Rate durch die Raumzeit bewegen, da jeder Vektor vom Nullpunkt (0,0) zu einem beliebigen Punkt des Kreisumfangs ja gleich dem Radius ist, also gleich lang und somit auch "gleich schnell".
Hoffe ich konnte transportieren, was mich grad beschäftigt.
Gruß,
Seeker |
|
 |
seeker_2208
Gast
|
 seeker_2208 Verfasst am: 15. Sep 2015 15:16 Titel: seeker_2208 Verfasst am: 15. Sep 2015 15:16 Titel: |
 |
|
kleine Korrektur:
where read
"daß sich alle Punkte auf der Geraden (die den flachen Raum darstellt) mit unterschiedlicher "Geschwindigkeit" durch die Zeit bewegen"
please read
"daß sich alle Punkte der Senkrechten (die den flachen Raum darstellt) in einem Quadrant mit unterschiedlicher "Geschwindigkeit" durch die Zeit bewegen."
Die Senkrechte liegt ja spiegelbildlich auf der x-Achse, somit gibt es immer zwei Punkt, die gleich schnell sind, einer mit Koordinate (x, +y) und einer mit (x, -y). |
|
 |
neuron
Anmeldungsdatum: 03.07.2011
Beiträge: 29
|
|
 |
neuron
Anmeldungsdatum: 03.07.2011
Beiträge: 29
|
 neuron Verfasst am: 16. Sep 2015 17:05 Titel: neuron Verfasst am: 16. Sep 2015 17:05 Titel: |
 |
|
|
Einschätzungen wären für mich interessant ... |
|
 |
Ich
Anmeldungsdatum: 11.05.2006
Beiträge: 913
Wohnort: Mintraching
|
 Ich Verfasst am: 16. Sep 2015 21:37 Titel: Ich Verfasst am: 16. Sep 2015 21:37 Titel: |
 |
|
Das Problem ist, dass deine Vorstellungen so kompliziert verwirrt sind, dass jeder Versuch der Aufklärung dich wahrscheinlich noch weiter verwirren wird.
Deine Diagramme sollen wohl kosmologische Zeit nach rechts und kosmologische "proper distance" nach oben darstellen? Wenn du nicht weißt, was das bedeutet, müsstest du dich erst darüber schlau machen. Wenn ja: Der kosmologische Raum, von dessen Krümmung man spricht, ist immer wie in deinem ersten Bild definiert, alle Punkte gleicher kosmologischer Zeit. Dementsprechend sieht er in deinem Diagramm immer wie eine gerade Linie aus. Die Krümmung kannst du im Bild nicht sehen, sie ist schon in deinen Koordinaten drin, das Bild selbst ist also verzerrt. Die Raumkrümmung ist grundsätzlich eine intrinsische Eigenschaft des Raums und nur in Spezialfällen als extrinsische Krümmung in deiner Raum-Zeit-Ebene sichtbar.
Ein solcher Spezialfall wäre, wenn das Diagramm einfach den flachen Minkowski-Raum darstellen soll. Das Universum wäre dann leer. Interessanterweise kann man auch das als expandierendes Friedmann-Modell darstellen. Hier wäre allerdings das zweite Diagramm eine Linie konstanter kosmologischer Zeit: Alle Punkte mit gleicher Eigenzeit seit dem Urknall liegen ja auf einer Hyperbel. Dieser Raum ist tatsächlich negativ gekrümmt. Dein erstes Diagramm entspräche der Gleichzeitigkeitslinie eine herausgegriffenen Beobachters, dessen "Normalraum" also. Der ist natürlich flach, wie es im leeren Universum sein muss. Du kannst über diesen Sezialfall unter "Milne-Universum" nachlesen.
Hilfreich? Ich fürchte nein. |
|
 |
neuron
Anmeldungsdatum: 03.07.2011
Beiträge: 29
|
 neuron Verfasst am: 17. Sep 2015 10:34 Titel: neuron Verfasst am: 17. Sep 2015 10:34 Titel: |
 |
|
Danke für Deinen Input, jedes Feedback welcome. Bin noch am lernen, deshalb erschließt sich mir nicht alles sofort.
| Ich hat Folgendes geschrieben: | | Das Problem ist, dass deine Vorstellungen so kompliziert verwirrt sind, dass jeder Versuch der Aufklärung dich wahrscheinlich noch weiter verwirren wird. |
Das sehe ich nicht ganz so, ich finde es legitim nach Krümmungsverhalten zu fragen, welches sich für mich nahezu aufdrängt, wenn man die FRW-Metrik in ein D2-Koordinatensystem übersetzt.
| Ich hat Folgendes geschrieben: | | Deine Diagramme sollen wohl kosmologische Zeit nach rechts und kosmologische "proper distance" nach oben darstellen? Wenn du nicht weißt, was das bedeutet, müsstest du dich erst darüber schlau machen. |
ja
| Ich hat Folgendes geschrieben: | | Der kosmologische Raum, von dessen Krümmung man spricht, ist immer wie in deinem ersten Bild definiert, alle Punkte gleicher kosmologischer Zeit. Dementsprechend sieht er in deinem Diagramm immer wie eine gerade Linie aus. |
verstanden, aber ich habe rein geometrische Überlegungen angestellt anhand
 \, (\dd r^2 + x^2 \, \dd \Omega))
und für speziell
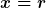

bei flach unter Verwendung der beiden o.a. Beziehungen, wo ist da die Krümmung bitte drinnen ? Mein Verständnis von "flach" ist "Krümmung = 0". Bitte korrigieren wenn ich falsch liege.
| Ich hat Folgendes geschrieben: | | Die Raumkrümmung ist grundsätzlich eine intrinsische Eigenschaft des Raums und nur in Spezialfällen als extrinsische Krümmung in deiner Raum-Zeit-Ebene sichtbar. |
Genau das möchte ich verstehen bzw. hinterfragen. Das Bildchen von mir zeigt eine 4D-Raumzeit dargestellt in einem D2-Koordinatensystem. Der Raum hat also einen Freiheitsgrad in den er sich krümmen könnte. Desweiteren ist meine Frage, wie/ob man eine Veränderungsrate des Raums in der Zeit untersuchen kann, d.h. mit welcher Rate sich der raum durch die Zeit bewegt. Geschwindigkeit im herkömmlichen Sinne scheint nicht zu passen, die ist gegeben mit "Strecke (Raum) pro Zeit" in der Raumzeit wäre das Equivalent m.M. etwas wie "Zeit pro X" aber was man als "X" nehmen könnte, da habe ich noch keine Idee ... |
|
 |
seeker_2208
Gast
|
 seeker_2208 Verfasst am: 21. Sep 2015 17:18 Titel: seeker_2208 Verfasst am: 21. Sep 2015 17:18 Titel: |
 |
|
Nochmal eine Verständnisfrage:
 \, (\dd r^2 + x^2 \, \dd \Omega))
was genau ist denn geometrisch gleich 0 wenn ds^2 = 0 gesetzt wird ? Bei ds^2 = 0 erhält man Informationen über lichtartige Ereignisse aus der Metrik, soweit klar, aber ausgehend von
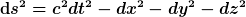
erhält man ja einen Kurvenabschnitt mit der Länge 0 wenn ds^2 = 0. Welche Punkte verbindet diese Kurve ?
Thx
seeker |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 21. Sep 2015 22:47 Titel: TomS Verfasst am: 21. Sep 2015 22:47 Titel: |
 |
|
ds = 0 bezeichnet den infinitesimalen Abstand einer beliebigen lichtartigen Kurve
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
seeker_2208
Gast
|
 seeker_2208 Verfasst am: 22. Sep 2015 10:40 Titel: seeker_2208 Verfasst am: 22. Sep 2015 10:40 Titel: |
 |
|
|
Danke. Aber Abstand zu was ? Abstand zum Koordinatenursprung, zum mitbewegten Beobachter, zwischen zwei Ereignissen ? |
|
 |
|
|















