| Autor |
Nachricht |
Mandelbrot20
Gast
|
 Mandelbrot20 Verfasst am: 16. Sep 2022 07:00 Titel: Unterschied Vektoren und Spinor |
 |
|
Hallo ich verstehe nicht was einen Spinor von einem Vektor unterscheidet. Ich rede hierbei noch nicht von einem Spinorfeld.
Es heißt, dass ein Spinor eine Darstellung der Gruppe SU(2) sei und letztlich in dem Darstellungsraum lebt. Da der Darstellungsraum ein Vektorraum ist, muss doch ein Spinor auch immer ein Vektor sein. Aber irgendwie soll es das dann doch nicht sein.
Liegt der Unterschied in der Konstruktion? Ko- und kontravariante Vektoren werden über Linearformen konstruiert, während Spinoren über besagte Darstellung konstruiert werden?
Sogesehen sind kovariante Vektoren, kontravariante Vektoren und Spinoren Vektoren (im Vektorraum-Sinne) und mit Spinoren gibt es Vektoren, die weder ko- noch kontravariant sind. Ist das so richtig?
Vielen Dank |
|
 |
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 16. Sep 2022 07:43 Titel: |
|
|
Spinoren sind zunächst mal Vektoren im Sinne der Definition eines linearen Vektorraumes.
Der Unterschied besteht in der Transformation unter Rotationen. Die Fundamentaldarstellung der Rotationsgruppe im n-dim Raum oder der n-dim Raumzeit entspricht der SO(n) bzw. SO(n,1); letztere umfasst neben den rein räumlich Rotationen auch Boosts.
Ein Ortsvektor r im n-dim Raum oder der n-dim Raumzeit transformiert unter R aus SO(n) bzw. SO(n,1) gemäß
Definiert man nun weitere physikalische Objekte psi (Spins in der Quantenmechanik, Spinorfelder wie in der Diracgleichung oder der QED) so ist mit der Transformation R, die auf r wirkt, eine Transformation S(R) verknüpft, die auf psi wirkt:
 \cdot \psi)
Am Beispiel der SO(3): r ist der Ortsvektor im 3-dim Raum, R ist eine 3^3 Rotationsmatrix. psi ist die Wellenfunktion der Pauligleichung, d.h. ein Spinorfeld bzgl. der Spin-Gruppe über dem 3-dim Raum; dies ist die SU(2), also die Gruppe der speziell unitären 2*2 Matrizen. Man stellt fest, dass eine 2:1 Abbildung zwischen SU(2) und SO(3) existiert
 \in SU(2) \to R \in SO(3) )
d.h für jede Rotation R existieren genau zwei Rotationen S(R). Diese kann man aus der expliziten Darstellung einer Rotationsmatrix R z.B. mittels Eulerwinkeln gewinnen. Eigentlich ist S das fundamentale Objekt, nicht R.
Für sich betrachtet ist der Spinor psi ein komplexer 2-Vektor, man kann Spinoren addieren, mit einem komplexen Skalar multiplizieren, es gibt ein Skalarprodukt usw. - alles, was man von einem Vektorraum erwartet.
Aber bzgl. der Rotationen S(R) verhalten sich Spinoren eben anders als herkömmliche Vektoren bzgl. der Rotationen R.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Mandelbrot20
Gast
|
| Mandelbrot20 Verfasst am: 16. Sep 2022 08:35 Titel: |
|
|
Danke für die Antwort TomS
Wäre denn die Aussage richtig, dass Spinoren keine Tensoren und damit weder ko- noch kontravariante Vektoren sind?
Also gibt es Vektoren, die weder ko noch kontravariant sind? |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 16. Sep 2022 08:47 Titel: |
|
|
Zugabe: Die Abbildung
 \to R(S) \in SO(3))
ist explizit gegeben durch
sigma bezeichnet die Pauli-Matrizen.
Diese Form ist in der Physik wenig hilfreich, man erkennt jedoch sofort, dass die Abbildung 2:1 ist, denn S und -S werden auf das selbe R abgebildet.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 16. Sep 2022 08:50 Titel: |
|
|
| Mandelbrot20 hat Folgendes geschrieben: | | Wäre denn die Aussage richtig, dass Spinoren keine Tensoren sind … |
Tensoren sind bzgl. einer Gruppe wie SO(n) „verallgemeinerte Vektoren“. Z.B. transformiert ein Tensor A zweiter Stufe gemäß
Mathematisch bedeutet dies, dass sie bzgl. einer anderen Darstellung der selben Gruppe transformieren.
| Mandelbrot20 hat Folgendes geschrieben: | | … und damit weder ko- noch kontravariante Vektoren sind? |
Vektoren und Tensoren sind an sich weder weder ko- noch kontravariant, das trifft nur auf ihre Komponenten bzgl. einer Basis zu.
Tensoren definieren einfach lineare Abbildungen, z.B. im Falle eines Tensors zweiter Stufe für zwei Vektoren
)
Das kannst du jetzt mittels Komponenten bzgl. verschiedener Basen ausdrücken:
 = x_\mu A^{\mu\nu} y_\nu = x_\mu A^{\mu}_{\nu} y^\nu = \ldots)
Erst dadurch kommen Ko- und Kontravarianz ins Spiel. Die Physiker unterscheiden oft nicht zwischen dem Objekt A und seiner Komponentendarstellung, das führt teilweise zur Verwirrung.
Die Darstellungen der SO(3) sind in denen der SU(2) enthalten. Sie werden durch einen nicht-negativen halbzahligen Wert s nummeriert. D.h.
Man kann auch für Spinoren höhere Darstellung betrachten, z.B. 3/2. Die Mathematiker sprechen tatsächlich für alle k von Tensoren bzgl. der SU(n), speziell bei halbzahligem s teilweise von Spinordarstellungen. Bei den Physikern ist das eher nicht üblich, bei ihnen ist der Begriff Tensor für ganzzahliges s reserviert.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Mandelbrot20
Gast
|
| Mandelbrot20 Verfasst am: 16. Sep 2022 09:20 Titel: |
|
|
| TomS hat Folgendes geschrieben: |
Vektoren und Tensoren sind an sich weder weder ko- noch kontravariant, das trifft nur auf ihre Komponenten bzgl. einer Basis zu.
Tensoren definieren einfach lineare Abbildungen, z.B. im Falle eines Tensors zweiter Stufe für zwei Vektoren
|
Wobei Mathematiker es ja erstmal komponentenfrei als Multilinearformen definieren. Und dadurch werden die Begriffe ko- und kontravarianter Tensor bereits definiert, wobei halt der Ursprung der Begriffe erst deutlich wird, wenn man eben das Verhalten unter Basistransformation betrachtet.
Mir ist es leider immer noch nicht so richtig klar.
Betrachten wir mal ein Vektorfeld auf einer Mannigfaltigkeit. Wenn ich nun einen Punkt x zu einem Punkt x' transformieren, dann transformiere ich dir Vektoren über einen pushforward.
Die transformierten Vektoren sind Tangentialvektoren, die in Tangentialräumen leben. Nach der Konstruktion von Tangentialvektoren (über Kurven oder Derivationen), handelt es sich um kontravariante Vektoren. Wenn man nun ein Spinorfeld auf der Mannigfaltigkeit hätte, könnten diese Spinoren nicht in denselben Tangentialräumen leben, weil sie ja nicht kontravariant transformieren. Heißt das man heftet an die Punkte der Mannigfaltigkeit noch weitere Vektorräume an in denen dann die Spinoren leben? Wenn ja, wie geht das?
Vielen Dank[/quote] |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 16. Sep 2022 10:11 Titel: |
|
|
Ich bin mir nicht sicher, ob ich dich da richtig verstehe.
Zunächst mal transformiert x nach x' nicht den Punkt P auf der Mannigfaltigkeit, sondern nur die Koordinaten des Punktes x(P) zu x'(P); der Punkt selbst bleibt fest.
Und unter Koordinatentransformation transformieren sich Skalar-, Vektor-, Tensor- und Spinor-Felder eben gemäß der entsprechenden Regeln, jedoch immer auf demselben Tangentialraum.
Erstens hat man für eine flache Mannigfaltigkeit in der SRT ohnehin nur einen Tangentialraum T, nicht einen T(P) je Punkt P. Und zweitens transformiert x nach x' wieder nur Koordinaten auf diesem einen Tangentialraum, nicht zwischen Tangentialräumen.
Und auf diesem Tangentialraum leben eben Felder F(P) mit Koordinatendarstellungen F(x); das können auch Spinorfelder sein.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Mandelbrot20
Gast
|
| Mandelbrot20 Verfasst am: 16. Sep 2022 11:45 Titel: |
|
|
| TomS hat Folgendes geschrieben: | Ich bin mir nicht sicher, ob ich dich da richtig verstehe.
Zunächst mal transformiert x nach x' nicht den Punkt P auf der Mannigfaltigkeit, sondern nur die Koordinaten des Punktes x(P) zu x'(P); der Punkt selbst bleibt fest.
|
Mit x meinte ich jetzt keine Koordinaten, sondern einen Punkt auf der Mannigfaltigkeit. Also sei M eine Mannigfaltigkeit, dann ist
Und dann kann ich ja eine Abbildung definieren, die von einem Punkt x nach einem Punkt x' abbildet. Ich spreche hier noch nicht von Koordinaten.
Die Tangentialvektoren werden dann über einen pushforward abgebildet.
Werden die Spinoren dann auch über den pushforward zwischend den Tangentialräumen abgebildet? |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 16. Sep 2022 12:24 Titel: |
|
|
| Mandelbrot20 hat Folgendes geschrieben: | Mit x meinte ich jetzt keine Koordinaten, sondern einen Punkt auf der Mannigfaltigkeit. Also sei M eine Mannigfaltigkeit, dann ist
Und dann kann ich ja eine Abbildung definieren, die von einem Punkt x nach einem Punkt x' abbildet. Ich spreche hier noch nicht von Koordinaten. |
Das ist ein aktiver Diffeomorphismus auf der Mannigfaltigkeit und hat i.A. nichts mit dem Transformationsverhalten unter Lorentztransformationen in einem Punkt zu tun.
| Mandelbrot20 hat Folgendes geschrieben: | | Werden die Spinoren dann auch über den pushforward zwischend den Tangentialräumen abgebildet? |
Äh, ja, nach meinem - leider sehr physikalischen - Verständnis - schon. Das hilft dir jetzt nicht wirklich weiter, oder?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Mandelbrot20
Gast
|
| Mandelbrot20 Verfasst am: 16. Sep 2022 15:31 Titel: |
|
|
| TomS hat Folgendes geschrieben: |
Äh, ja, nach meinem - leider sehr physikalischen - Verständnis - schon. Das hilft dir jetzt nicht wirklich weiter, oder? |
Gehen wir lieber nochmal einen Schritt zurück und betrachten die Gruppe Spin(3). Mir ist nämlich noch nicht klar, wie jetzt genau die Drehung im R^3 mit der Drehung von Elementen aus Spin(3) verknüpft ist.
Meines Wissens nach bildet sich Spin(3) aus einer Clifford-Algebra und diese Algebra hat in diesem speziellen Fall eine quadratische Form auf dem R^3.
Die quadratische Form sieht bei Spin(3) so aus:
=x_1^2+x_2^2+x_3^2)
D.h. die unterliegende Struktur ist der R^3. Bedeutet das jetzt, dass eine Drehung von Vektoren dieses R^3 sich "überträgt" auf die Vektoren von Spin(3) und wenn ja wieso?
Bei Tensoren ist es ja so ähnlich. Man hat als unterliegende Struktur einen Vektorraum und basierend auf diesem Vektorraum baut man sich die Multilinearformen. Transformationen in diesem Vektorraum übertragen sich dann auf die Komponenten der Multilinearformen, was für mich auch nachvollziehbar ist.
Bei den Spinoren ist es halt so, dass man Drehungen in einem Raum R^3 hat und ich versteh dann nicht wieso das sich dann auf die Spinoren überträgt.
Verstehst du jetzt besser wo mein Verständnisproblem ist? |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 16. Sep 2022 16:23 Titel: |
|
|
| Mandelbrot20 hat Folgendes geschrieben: | | … und betrachten die Gruppe Spin(3). Mir ist nämlich noch nicht klar, wie jetzt genau die Drehung im R^3 mit der Drehung von Elementen aus Spin(3) verknüpft ist. |
Ich denke, du hängst zu sehr an der Dimension des Ortsraumes und der Mannigfaltigkeit; du solltest von der Gruppentheorie her kommen.
Du hast eine abstrakte Gruppe SU(2). Diese Gruppe wird durch drei reelle Parameter (Drehwinkel) parametrisiert.
Dann hast du verschiedenere Darstellungen rep SU(2) die du mir s nummerierst; s läuft über halbzahlige positive Zahlen. Die Dimension jeder Darstellung rep s ist dim rep s = 2s+1 d.h. es handelt sich um (2s+1)*(2s+1) Matrizen. Die Darstellung s = 1/2 entspricht den dir vertrauten SU(2) Matrizen, die Darstellung s = 1 den SO(3) Matrizen. Für ganzzahlige s entsprechen die Darstellungen der SU(2) denen der SO(3).
Die Darstellungen zeichnen sich insbs. dadurch aus, dass für beliebige Gruppenelemente g, h in beliebigen Darstellungen gilt:
 \cdot \text{rep}(h) = \text{rep}(g \cdot h))
Die Matrizen der Darstellungen wirken auf entsprechenden Vektorräumen. Ganz speziell für s = 1 kann dies der 3-dim. Ortsraum sein, muss aber nicht.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Mandelbrot20
Gast
|
| Mandelbrot20 Verfasst am: 16. Sep 2022 18:32 Titel: |
|
|
Ok dann nähern wir uns dem mal von der Gruppentheorie an.
Ich gebe erstmal wieder, was bisher mein Verständnis davon ist.
Ausgangspunkt ist SU(2) und das Ziel ist es die irreduziblen Darstellungen dieser Gruppe zu identifizieren. Dazu betrachtet man die zugehörige liealgbra su(2) mit der Basis
 und sucht dazu erstmal die irreduziblen Darstellungen
Dabei gelten die üblichen Kommutatorrelationen der Drehimpulsalgebra.
Jetzt nehme man, man habe eine Darstellung mit einem Darstellungsraum V gefunden. Dann gibt es Operatoren ) , die dann in dieser Darstellung den ursprünglichen Operatoren entsprechen und Abbildungen zwischen Vektoren darstellen. So stellt man fest, dass  nicht die Eigenzustände des Casimir-Operators  ändern und damit eben der Raum der Eigenvektoren von J^2 zu festem Eigenwert j nie verlassen wird, weshalb der Vektorraum V auf dem man mit festem j operiert Invariant ist und man damit eine irreduzible Darstellung zu jedem j hat. Zu der Liegruppe kommt man dann über die Exponentialabbildung.
Ist das in etwa richtig? |
|
|
Mandelbrot20
Gast
|
| Mandelbrot20 Verfasst am: 16. Sep 2022 18:57 Titel: |
|
|
Mein Problem ist jetzt insbesondere, dass ich nicht verstehe warum der Spinor , \psi(x)) sich auf bestimmte Weise transformieren muss, wenn man die Koordinaten von x nach x' transformiert. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 16. Sep 2022 20:00 Titel: |
|
|
| Mandelbrot20 hat Folgendes geschrieben: | | Ist das in etwa richtig? |
Ja.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 16. Sep 2022 20:05 Titel: |
|
|
| Mandelbrot20 hat Folgendes geschrieben: | | Mein Problem ist jetzt insbesondere, dass ich nicht verstehe warum der Spinor sich auf bestimmte Weise transformieren muss, wenn man die Koordinaten von x nach x' transformiert. |
Weil es sonst kein Spinorfeld ist; das ist letztlich die Definition.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Mandelbrot20
Gast
|
| Mandelbrot20 Verfasst am: 16. Sep 2022 20:31 Titel: |
|
|
| TomS hat Folgendes geschrieben: |
Weil es sonst kein Spinorfeld ist; das ist letztlich die Definition. |
Ich glaube das ist wirklich der Punkt wo es bei mir hapert.
Besteht die Definition also darin, dass ein Weyl-Spinorfeld bei einer Transformation der Ortskoordinaten sich wie ein Weyl-Spinor transformiert?
Also sagen wir mal wir haben eine Transformation der Koordinaten:
 & -sin(\phi) & 0 \\ sin(\phi) & cos(\phi) & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} )
Dann ist es Teil der Definition des Spinorfelds, dass er sich so transformieren muss?
 \\ \psi'(x') \end{pmatrix} = \begin{pmatrix} cos(\phi/2) & -sin(\phi/2) \\ sin(\phi/2) & cos(\phi/2) \end{pmatrix} \begin{pmatrix} \phi(x) \\ \psi(x) \end{pmatrix} )
Bisher bin ich davon ausgegangen, dass man irgendwie schließen kann, dass sich das Spinorfeld so transformiert, wenn sich die Ortskoordinaten transformieren.
Bei der Dirac-Gleichung hat man bspw Diracspinoren als Lösung. Schließt man nur deshalb darauf, dass es sich um Diracspinoren handelt, weil die Dirac-Gleichung nur dann lorentzinvariant ist? Legt man das dann einfach nur fest und man kann nicht anderweitig herleiten, dass es sich um Dirac-Spinoren handelt?
Um das ganze für mich noch etwas klarer machen. Man betrachtet erstmal einfach nur Spinoren (ohne Feld). Diese Spinoren leben in Darstellungsräumen von SU(2). Die Darstellungen kann ich durch (halb und ganzzahlige) Eigenwerte eines Casimir-Operators "nummerieren". Spinoren sind eigentlich nur die Darstellungen mit halbzahligen Werten. SU(2) kann ich durch drei Parameter parametrisieren.
Ordne ich nun jedem Punkt des Ortsraumes einen Spinor mit der Darstellung für j=1/2 zu, erhalte ich ein Feld und per definitionem muss dieses Feld sich wie oben genannt transformieren. Für Spinoren mit j=3/2 sähe die Transformation entsprechend anders aus.
Unklar ist mir noch wie ich den Zusammenhang zwischen den Drehwinkeln des Ortsraumes und den Parametern der SU(2) hinbekomme.
Ich habe im obigen Beispiel ja nur ne simple Drehung um die z-Achse mit nur einem Winkel beschrieben. Aber wie weiß ich, dass dieser Drehwinkel nun dem entsprechenden Parameter der SU(2) entspricht |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
| jh8979 Verfasst am: 16. Sep 2022 22:11 Titel: |
|
|
| Mandelbrot20 hat Folgendes geschrieben: |
Bei der Dirac-Gleichung hat man bspw Diracspinoren als Lösung. Schließt man nur deshalb darauf, dass es sich um Diracspinoren handelt, weil die Dirac-Gleichung nur dann lorentzinvariant ist? Legt man das dann einfach nur fest und man kann nicht anderweitig herleiten, dass es sich um Dirac-Spinoren handelt?
|
Ja, das kann man so sehen. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 16. Sep 2022 22:34 Titel: |
|
|
| Mandelbrot20 hat Folgendes geschrieben: | | Besteht die Definition also darin, dass ein Weyl-Spinorfeld bei einer Transformation der Ortskoordinaten sich wie ein Weyl-Spinor transformiert? |
Ja.
| Mandelbrot20 hat Folgendes geschrieben: | | Bisher bin ich davon ausgegangen, dass man irgendwie schließen kann, dass sich das Spinorfeld so transformiert, wenn sich die Ortskoordinaten transformieren. |
Zunächst überträgt sich die Lorentztransformation der Koordinaten in irgendeiner Form auf eine Transformation der Felder. Man fordert Lorentzkovarianz, woraus logischerweise folgt, dass die Transformation der Felder einer Darstellung der selben Gruppe angehören muss wie die Transformation der Koordinaten.
| Mandelbrot20 hat Folgendes geschrieben: | | Bei der Dirac-Gleichung hat man bspw Diracspinoren als Lösung. Schließt man nur deshalb darauf, dass es sich um Diracspinoren handelt, weil die Dirac-Gleichung nur dann lorentzinvariant ist? Legt man das dann einfach nur fest und man kann nicht anderweitig herleiten … |
Man kann mathematisch lediglich herleiten, dass Darstellungen der Lorentzgruppe vorliegen müssen, jedoch nicht welche. Hier hat man eine Wahlfreiheit.
| Mandelbrot20 hat Folgendes geschrieben: | Man betrachtet erstmal einfach nur Spinoren (ohne Feld). Diese Spinoren leben in Darstellungsräumen von SU(2). Die Darstellungen kann ich durch (halb und ganzzahlige) Eigenwerte eines Casimir-Operators "nummerieren". Spinoren sind eigentlich nur die Darstellungen mit halbzahligen Werten. SU(2) kann ich durch drei Parameter parametrisieren.
Ordne ich nun jedem Punkt des Ortsraumes einen Spinor mit der Darstellung für j=1/2 zu, erhalte ich ein Feld und per definitionem muss dieses Feld sich wie oben genannt transformieren. |
Ja.
| Mandelbrot20 hat Folgendes geschrieben: | | Unklar ist mir noch wie ich den Zusammenhang zwischen den Drehwinkeln des Ortsraumes und den Parametern der SU(2) hinbekomme. |
Das wird in diversen Büchern gezeigt. Evtl. klebe ich morgen einfach eine Kopie hier rein.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Mandelbrot20
Gast
|
| Mandelbrot20 Verfasst am: 16. Sep 2022 22:46 Titel: |
|
|
| TomS hat Folgendes geschrieben: |
Zunächst überträgt sich die Lorentztransformation der Koordinaten in irgendeiner Form auf eine Transformation der Felder. Man fordert Lorentzkovarianz, woraus logischerweise folgt, dass die Transformation der Felder einer Darstellung der selben Gruppe angehören muss wie die Transformation der Koordinaten. |
Ist mit lorentzkovarianz dasselbe gemeint wie mit lorentzinvarianz?
| Zitat: | | Das wird in diversen Büchern gezeigt. Evtl. klebe ich morgen einfach eine Kopie hier rein. |
Gerne  |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 16. Sep 2022 23:07 Titel: |
|
|
Lorentzkovarianz ist grob gesprochen die Eigenschaft, dass ein definiertes Transformationsverhalten eines Objektes vorliegt, dass es also bzgl. einer Tensor- oder Spinordarstellung transformiert. Mittels geeigneter Kombinationen derartiger Objekte kann man Lorentzinvarianten konstruieren, siehe z.B. der Term
in der Dirac-Wirkung.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Mandelbrot20
Gast
|
| Mandelbrot20 Verfasst am: 17. Sep 2022 22:18 Titel: |
|
|
Ich habe grad noch ne Überlegung gehabt.
Wenn ich eine Rotation im Ortsraum durchführe, zieht dies eine Transformation der Felder nach sich, wobei die Transformation davon abhängt, um welche Darstellung der Lorentzgruppe es sich bei dem Feld handelt (Skalar, Spinor, Tensor...)
Wenn nun für die Felder eine Lagrangedichte vorliegt und diese Lagrangedichte oder besser gesagt die entsprechende Wirkung Invariant gegenüber beliebiger Drehungen ist, muss ja irgendwie der Drehimpuls nach dem Noether-Theorem herauspurzeln.
Meinem Verständnis nach kann man den Ausdruck für den Drehimpuls, der sich daraus ergibt, dann in zwei Terme zerlegen. Einer der durch die Änderung des Ortes zustande kommt und einer durch die damit verbundene Änderung der Feldkomponenten. Der Anteil, der von der Ortsdrehung kommt, entspräche dann dem Bahndrehimpuls, während der zweite Teil, der durch die Feldänderung entsteht, sowas wie eine innere Symmetrie des Feldes ist und letztlich dem Spin entspricht. Stimmt das?
Wenn man die Felder dann noch quantisiert, müsste man daraus doch einen Spinoperator erhalten oder? Photonen werden durch ein Vierervektorfeld beschrieben. Dafür müsste der Spinoperator doch den Wert 1 und für Elektronen, die durch Dirac-Spinoren beschrieben werden den Wert 1/2 messen oder? |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 19. Sep 2022 20:06 Titel: |
|
|
| Mandelbrot20 hat Folgendes geschrieben: | Wenn ich eine Rotation im Ortsraum durchführe, zieht dies eine Transformation der Felder nach sich, wobei die Transformation davon abhängt, um welche Darstellung der Lorentzgruppe es sich bei dem Feld handelt (Skalar, Spinor, Tensor...)
Wenn nun für die Felder eine Lagrangedichte vorliegt und diese Lagrangedichte oder besser gesagt die entsprechende Wirkung Invariant gegenüber beliebiger Drehungen ist, muss ja irgendwie der Drehimpuls nach dem Noether-Theorem herauspurzeln. |
Ja.
| Mandelbrot20 hat Folgendes geschrieben: | | Meinem Verständnis nach kann man den Ausdruck für den Drehimpuls, der sich daraus ergibt, dann in zwei Terme zerlegen. Einer der durch die Änderung des Ortes zustande kommt und einer durch die damit verbundene Änderung der Feldkomponenten. |
In gewisser Weise - siehe (10.104) in https://userswww.pd.infn.it/~zwirner/DT-ch10-fin.pdf
| Mandelbrot20 hat Folgendes geschrieben: | | Der Anteil, der von der Ortsdrehung kommt, entspräche dann dem Bahndrehimpuls, während der zweite Teil, der durch die Feldänderung entsteht, sowas wie eine innere Symmetrie des Feldes ist und letztlich dem Spin entspricht. Stimmt das? |
Ja (aber man spricht hier nicht von innerer Symmetrie, da auch der Sin mit der Raumzeit verknüpft ist)
Wobei man vorsichtig sein muss, denn die beiden Terme dieses relativistischen Drehimpulsoperator kommutieren zwar untereinander, liefern jedoch einzeln keine Symmetrie der Diracgleichung
| Mandelbrot20 hat Folgendes geschrieben: | | Wenn man die Felder dann noch quantisiert, müsste man daraus doch einen Spinoperator erhalten oder? |
Was genau meinst du mit quantisieren?
Den Übergang zur Quantenfeldtheorie mit Erzeugern und Vernichtern, also die zweite Quantisierung? Dann folgen die Drehimulsoperatoren aus Integralen über Dichten, die bilinear in den Feldern sind und die o.g. Generatoren enthalten.
Oder einfach die Diracgleichung als Schrödingergleichung der relativistischen Quantenmechanik? Dann liefert (10.104) direkt die Drehimulsoperatoren, die auf das Spinorfeld = die Wellenfunktion wirken.
| Mandelbrot20 hat Folgendes geschrieben: | | Photonen werden durch ein Vierervektorfeld beschrieben. Dafür müsste der Spinoperator doch den Wert 1 und für Elektronen, die durch Dirac-Spinoren beschrieben werden den Wert 1/2 messen oder? |
Letzteres ja, ersteres leider nein.
Man kann das Viererpotential des elektromagnetischen Feldes nicht als Wellenfunktion auffassen, auf das dann entsprechende Operatoren wirken. Außerdem werden Photonen nicht durch vier reelle Felder beschrieben, da aufgrund der Eichsymmetrie zwei Felder eliminiert werden (müssen). D.h. diese Darstellung der Poincaregruppe für masselose Felder entspricht lax gesprochen nicht S = 1 mit dim rep = 3, sondern dim rep = 2, entsprechend der zwei physikalischen Polarisationen (Helizitäten).
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Mandelbrot20
Gast
|
| Mandelbrot20 Verfasst am: 22. Sep 2022 22:35 Titel: |
|
|
| TomS hat Folgendes geschrieben: |
W
Was genau meinst du mit quantisieren?
Den Übergang zur Quantenfeldtheorie mit Erzeugern und Vernichtern, also die zweite Quantisierung? Dann folgen die Drehimulsoperatoren aus Integralen über Dichten, die bilinear in den Feldern sind und die o.g. Generatoren enthalten.
Oder einfach die Diracgleichung als Schrödingergleichung der relativistischen Quantenmechanik? Dann liefert (10.104) direkt die Drehimulsoperatoren, die auf das Spinorfeld = die Wellenfunktion wirken.
|
Ich meinte Ersteres, also den Übergang zur Quantenfeldtheorie, insbesondere denke ich dabei an die kanonische Quantisierung. Da würde ich noch gerne genauer drauf eingehen, weil ich da noch ziemliche Verständnisprobleme habe.
So wie ich es bisher verstehe, bedeutet dies, dass die Felder zu Feldoperatoren werden und diese Feldoperatoren bestimmte Kommutator oder Antikommutatorrelationen erfüllen. Die Feldoperatoren wirken dabei auf Fockzustände. Da habe ich aber ein grundlegendes Vorstellungsproblem.
Soweit ich weiß sind die Felder der Quantenfeldtheorien omnipräsent, d.h. es gibt bspw genau ein Elektronenfeld und genau ein Photonenfeld. Diese Felder können angeregt werden, was bspw einer Teilchenerzeugung entspricht. Die Erzeugung eines Photons ist sowas wie eine Elementaranregung des Photonenfelds. Mathematisch ausgedrückt wird dies auch die Anwendung eines Erzeugungsoperators. Ist das richtig?
Jetzt ist es so, dass ich mir bei einem klassischen Feld gut vorstellen kann, wie es den gesamten Raum ausfüllt. Man ordnet ja einfach jedem Raumpunkt einen Skalar, Spinor, Tensor ... zu.
Bei Feldoperatoren kann ich mir das irgendwie nicht vorstellen.
Bedeutet ) dass jedem Punkt x ein Operator zugeordnet wird. Andererseits wende ich aber den Operator am Ort x auf einen Fockzustand an also bspw auf den Vakuum zustand  |0>) , wobei der abstrakte Fockzustand zunächst gar keinen Bezug zu einem Ort hat. Das Ergebnis ist dann ein Teilchen, welches am Ort x lokalisiert ist oder? |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 22. Sep 2022 23:41 Titel: |
|
|
Sollten wir besser in einem eigenen Thread behandeln.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Mandelbrot20
Gast
|
| Mandelbrot20 Verfasst am: 23. Sep 2022 10:21 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | Sollten wir besser in einem eigenen Thread behandeln. |
ich habe dazu einen weiteren Thread eröffnet.
Eine Frage kam mir noch zu den Transformationen.
Die newtonsche Bewegungsgleichung mit einer konstanten Kraft hat eine Translationsinvarianz, aber es gilt keine Impulserhaltung. Liegt das daran, dass die Translationssymmetrie zwar für die DGL, nicht aber für die Wirkung gilt? Und Noether nur Symmetrien der Wirkung betrachtet?
Und noch eine Frage:
In Büchern habe ich gelesen, wie die Ortsdarstellung des Impulsoperators über Translationen hergeleitet wurde. Man machte dabei eine aktive Transformation
 nach 
Das würde eine Funktion ) um a Einheiten nach rechts verschieben. Es wurde dann diese Funktion betrachtet ) aber meiner Meinung nach müsste die transformierte Funktion dann so aussehen ) Stimmt das? |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 23. Sep 2022 12:51 Titel: |
|
|
| Mandelbrot20 hat Folgendes geschrieben: | Eine Frage kam mir noch zu den Transformationen.
Die newtonsche Bewegungsgleichung mit einer konstanten Kraft hat eine Translationsinvarianz, aber es gilt keine Impulserhaltung. Liegt das daran, dass die Translationssymmetrie zwar für die DGL, nicht aber für die Wirkung gilt? Und Noether nur Symmetrien der Wirkung betrachtet? |
Letztlich ja.
Natürlich erscheint
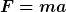
invariant unter Translation, aber es zeigt ja direkt, dass
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 23. Sep 2022 14:40, insgesamt einmal bearbeitet |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 23. Sep 2022 14:19 Titel: |
|
|
| Mandelbrot20 hat Folgendes geschrieben: |
Eine Frage kam mir noch zu den Transformationen.
Die newtonsche Bewegungsgleichung mit einer konstanten Kraft hat eine Translationsinvarianz, aber es gilt keine Impulserhaltung. Liegt das daran, dass die Translationssymmetrie zwar für die DGL, nicht aber für die Wirkung gilt? Und Noether nur Symmetrien der Wirkung betrachtet?
|
Ja, der Zusammenhang zwischen Symmetrien und Erhaltungsgrößen gilt nur für kontinuierliche Symmetrien der Wirkung.
Aber, zu diesen Symmetrien zählen auch Transformationen, die die Lagrangefunktion um lediglich eine totale Zeitableitung (und die Wirkung somit nur um Randterme) ändern. Eine räumliche Translation ändert die Lagrangefunktion
lediglich um
.)
Dazu gehört die Erhaltungssgröße  , deren Konstanz in der Zeit äquivalent mit der Bewegungsgleichung ist.
| Zitat: |
Und noch eine Frage:
In Büchern habe ich gelesen, wie die Ortsdarstellung des Impulsoperators über Translationen hergeleitet wurde. Man machte dabei eine aktive Transformation
nach
Das würde eine Funktion um a Einheiten nach rechts verschieben. Es wurde dann diese Funktion betrachtet aber meiner Meinung nach müsste die transformierte Funktion dann so aussehen Stimmt das? |
Die "transformierte Funktion" ist nichts anderes als die Verkettung  \equiv f^\ast\psi(x) \stackrel{\text{def}}{=} \psi(f(x))) . (Das definiert man so, damit  auch für nichtumkehrbare Funktionen f sinnvoll ist.)
Für  = x + a) gilt also  = \psi(x+a)) oder  = \psi(x)) .
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
|
Mandelbrot20
Gast
|
| Mandelbrot20 Verfasst am: 23. Sep 2022 16:56 Titel: |
|
|
[quote="index_razor"]
Aber, zu diesen Symmetrien zählen auch Transformationen, die die Lagrangefunktion um lediglich eine totale Zeitableitung (und die Wirkung somit nur um Randterme) ändern. Eine räumliche Translation ändert die Lagrangefunktion
lediglich um
Dazu gehört die Erhaltungssgröße , deren Konstanz in der Zeit äquivalent mit der Bewegungsgleichung ist.
[/latex]
Diese Größe hat dann aber nichts mit dem Impuls zu tun oder? Impuls ist ja diejenige Erhaltungsgröße, die mir Raumtranslationsinvarianz zusammenhängt. Müsste man es damit ergänzen, dass es nur ein Impuls ist, wenn die Lagrangefunktion diese Symmetrie hat?
| Zitat: |
Die "transformierte Funktion" ist nichts anderes als die Verkettung . (Das definiert man so, damit auch für nichtumkehrbare Funktionen f sinnvoll ist.)
Für gilt also oder . |
Für mich erscheint es irgendwie natürlicher so zu definieren:
 \equiv f^\ast\psi(x) \stackrel{\text{def}}{=} \psi(f^{-1}(x))) .
In deinem Fall transformiert die Funktion f doch von den neuen Werten zu den alten Werten oder nicht? |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 23. Sep 2022 17:59 Titel: |
|
|
| Mandelbrot20 hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: |
Aber, zu diesen Symmetrien zählen auch Transformationen, die die Lagrangefunktion um lediglich eine totale Zeitableitung (und die Wirkung somit nur um Randterme) ändern. Eine räumliche Translation ändert die Lagrangefunktion
lediglich um
Dazu gehört die Erhaltungssgröße , deren Konstanz in der Zeit äquivalent mit der Bewegungsgleichung ist.
|
Diese Größe hat dann aber nichts mit dem Impuls zu tun oder? |
Diese Größe ist die Differenz aus Impuls und Kraftstoß.
| Zitat: |
Impuls ist ja diejenige Erhaltungsgröße, die mir Raumtranslationsinvarianz zusammenhängt. Müsste man es damit ergänzen, dass es nur ein Impuls ist, wenn die Lagrangefunktion diese Symmetrie hat? |
Ja, die Frage ist eben, was du unter Raumtranslationsinvarianz verstehst, also welche Größe genau invariant sein soll. Wenn du Invarianz unter der vollen Galileigruppe forderst, tritt dieser Sonderfall auch nicht auf. Siehe auch diesen Thread.
| Zitat: |
| Zitat: |
Die "transformierte Funktion" ist nichts anderes als die Verkettung . (Das definiert man so, damit auch für nichtumkehrbare Funktionen f sinnvoll ist.)
Für gilt also oder . |
Für mich erscheint es irgendwie natürlicher so zu definieren:
.
In deinem Fall transformiert die Funktion f doch von den neuen Werten zu den alten Werten oder nicht? |
Deswegen heißt die Operation auch "pullback". Im Falle umkehrbarer Funktionen f ist natürlich auch der pushforwad  sinnvoll. Aber da der pullback praktisch für alle glatten f definiert ist, ist er eigentlich die natürlichere Operation für Funktionen.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
|
Mandelbrot20
Gast
|
| Mandelbrot20 Verfasst am: 23. Sep 2022 19:07 Titel: |
|
|
| index_razor hat Folgendes geschrieben: |
Deswegen heißt die Operation auch "pullback". Im Falle umkehrbarer Funktionen f ist natürlich auch der pushforwad sinnvoll. Aber da der pullback praktisch für alle glatten f definiert ist, ist er eigentlich die natürlichere Operation für Funktionen. |
Das versteh ich nicht. Wenn ich jeden Punkt x transformiere von x nach x'=x+a. (a > 0) Dann transformiert sich die Funktion
=x^2) doch zu der nach rechts verschobenen Funktion =(x-a)^2) , weil doch jeder Punkt um a Einheiten nach rechts Wandert und damit auch der "Graph" der Funktion um a Einheiten nach rechts wandert. und ich bekomme dann doch nicht die nach links verschobene Funktion
=(x+a)^2) |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 23. Sep 2022 19:19 Titel: |
|
|
| Mandelbrot20 hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: |
Deswegen heißt die Operation auch "pullback". Im Falle umkehrbarer Funktionen f ist natürlich auch der pushforwad sinnvoll. Aber da der pullback praktisch für alle glatten f definiert ist, ist er eigentlich die natürlichere Operation für Funktionen. |
Das versteh ich nicht. Wenn ich jeden Punkt x transformiere von x nach x'=x+a. (a > 0) Dann transformiert sich die Funktion
doch zu der nach rechts verschobenen Funktion , weil doch jeder Punkt um a Einheiten nach rechts Wandert und damit auch der "Graph" der Funktion um a Einheiten nach rechts wandert. und ich bekomme dann doch nicht die nach links verschobene Funktion
|
Der pushforward verschiebt (wenn er definiert ist) nach rechts in Richtung der Punkttransformation, der pullback verschiebt nach links entgegen der Transformation. Die erste Operation bezeichnet man deshalb manchmal auch als "kovariant", die zweite als "kontravariant". (Allerdings verwenden Physiker diese Begriffe meist etwas anders.) Offenbar verwendet deine Quelle den pullback, vielleicht weil er allgemeiner ist. Was ist daran so rätselhaft?
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
|
Mandelbrot20
Gast
|
| Mandelbrot20 Verfasst am: 23. Sep 2022 20:43 Titel: |
|
|
| index_razor hat Folgendes geschrieben: | | Offenbar verwendet deine Quelle den pullback, vielleicht weil er allgemeiner ist. Was ist daran so rätselhaft? |
Ich verstehe nicht wieso das Skalarfeld bei der Transformation nicht der Punkttransformation folgen muss und ich dachte ko- und kontravariant gibt es nicht bei Skalarfeldern, sondern erst bei Tensorfeldern 1. und höherer Stufe. |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 24. Sep 2022 09:05 Titel: |
|
|
| Mandelbrot20 hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Offenbar verwendet deine Quelle den pullback, vielleicht weil er allgemeiner ist. Was ist daran so rätselhaft? |
Ich verstehe nicht wieso das Skalarfeld bei der Transformation nicht der Punkttransformation folgen muss und ich dachte ko- und kontravariant gibt es nicht bei Skalarfeldern, sondern erst bei Tensorfeldern 1. und höherer Stufe. |
Wie gesagt verwenden Physiker die beiden Begriffe "kovariant" und "kontravariant" anders als ich gerade. Siehe z.B. Baez, Muniain, Gauge Fields, Knots, and Gravity, Kapitel 3 für eine ausführliche Erklärung in welchem Sinne Vektoren kovariant und Skalarfelder und Differentialformen kontravariant sind und warum das teilweise genau umgekehrt zur Physikersprechweise ist (oder auch hier).
Die natürliche Operation von Skalarfelderen unter beliebigen glatten Abbildungen ist der pullback. Das ist ein kontravarianter Funktor. Wenn die Abbildung nicht invertierbar ist, ist dies auch die einzige Operation, die möglich ist. In spezielleren Situationen, wie z.B. bei der Betrachtung von Symmetriegruppen, deren Elemente immer invertierbar sind, definiert man aber auch andere Operationen auf Skalarfeldern, z.B. den pushforward . Das muß man sogar tun, wenn man z.B. aus einer Gruppenwirkung auf der Menge M eine Darstellung auf der Menge von skalaren Funktionen auf M definieren will. Denn nur der pushforward liefert einen Gruppenhomomorphismus
^{-1} = \psi\circ T_{h}^{-1}\circ T_{g}^{-1} = T_{g\ast} T_{h\ast} \psi)
Mit dem pullback funktioniert das im allgemeinen nicht, denn der vertauscht die Reihenfolge  . Allerdings spielt es wiederum keine Rolle, wenn die Gruppe kommutativ ist, wie im Fall von Translationen. Es hängt also nur vom Kontext ab, welche der beiden Operationen verwendet werden muß oder überhaupt verwendet werden kann. Ohne den Zusammenhang kann man schlecht beurteilen was deine Quelle tut. Aber solange sie damit konsistent bleibt, sehe ich erstmal kein Problem.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
|
|
|
Registrieren
Login
FAQ
Suchen
