| Autor |
Nachricht |
terminus
Anmeldungsdatum: 17.10.2020
Beiträge: 555
|
 terminus Verfasst am: 16. Nov 2020 14:16 Titel: Verständnisfrage zu Dirac-Notation und Vektoren terminus Verfasst am: 16. Nov 2020 14:16 Titel: Verständnisfrage zu Dirac-Notation und Vektoren |
 |
|
hallo,
(Anm.: ich finde keinen Weg, n oder m mit Zirkumflex oben drauf zu schreiben... - edit: verbessert! )
Zitat:
| Zitat: | Beginnen wir mit einem längs 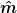 orientierten A (gemeint ist wohl der Ausrichtungsvektor einer Spin-Messapparatur) und bestätigen orientierten A (gemeint ist wohl der Ausrichtungsvektor einer Spin-Messapparatur) und bestätigen 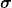 = +1, so ergeben nachfolgende Messungen mit A orientiert längs = +1, so ergeben nachfolgende Messungen mit A orientiert längs 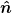 das statistische Resultat das statistische Resultat
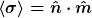 |
Fragen:
1.) ich kenne zwar die Schreibweisen |x> (Ket) und <y| (Bra) und <x|y> (BraKet), aber was genau ist 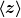 oder oder 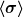 ? ?
2.) wie wird die (Punkt?-) Multiplikation von 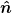 und und 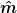 ausgerechnet? ist damit <n|m> gemeint oder etwas anderes? ausgerechnet? ist damit <n|m> gemeint oder etwas anderes?
edit:
1) scheint wohl kein Bra oder Ket etc zu sein, sondern nur eine Schreibweise für einen Erwartungswert, hat also wohl nichts mit den Bra/Ket-Pfeilsymbolen < > zu tun - warum kann man dann aber nicht ganz auf < > verzichten und einfach nur 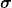 schreiben ...? schreiben ...?
2) scheint sich um das Innere Produkt zu handeln (|n|*|m|*cos (φ) )...?
_________________
αΓγΔδεζηΘθικλµνΞξΠπϱΣστΦφχΨψΩω∫∂ħ⋅⟨⟩√≤≥∞∈
Zuletzt bearbeitet von terminus am 19. Nov 2020 14:50, insgesamt 3-mal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 16. Nov 2020 16:39 Titel: TomS Verfasst am: 16. Nov 2020 16:39 Titel: |
 |
|
Dein Post ist schwer zu lesen.
Zur 1)
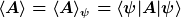
bezeichnet den Erwartungswert des Operators A im Zustand psi, wobei letzterer manchmal nicht notiert wird.
Zu 2)
Ist für mich nicht lesbar. Was soll n^ sein ??
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
terminus
Anmeldungsdatum: 17.10.2020
Beiträge: 555
|
 terminus Verfasst am: 16. Nov 2020 17:02 Titel: terminus Verfasst am: 16. Nov 2020 17:02 Titel: |
 |
|
zu 1)
hmmh - wegen <A> oder <σ>:
verstehe ich jetzt nicht ganz, von einem psi (ψ) ist nirgends die Rede...?
Nur von einem σ oder <σ>
zu 2)
| Zitat: | | Was soll n^ sein ?? |
schrieb ich ganz oben: ein n mit einem ^ (Zirkumflex) oben drauf, so wie bei â (ich kann das Zeichen mit dem n oder m nicht schreiben)
_________________
αΓγΔδεζηΘθικλµνΞξΠπϱΣστΦφχΨψΩω∫∂ħ⋅⟨⟩√≤≥∞∈ |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 16. Nov 2020 17:12 Titel: TomS Verfasst am: 16. Nov 2020 17:12 Titel: |
 |
|
Zu (1) kenne ich nur die Bedeutung des Erwartungswertes.
Bei (2) meinst du wohl
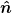
Das bezeichnet einen Einheitsvektor, z.B. im Ortsraum:
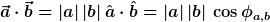
Gerade bei Spinoren wird oft auch nicht sauber zwischen dem Ket und den Komponenten des 2-Spinors unterschieden.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
terminus
Anmeldungsdatum: 17.10.2020
Beiträge: 555
|
 terminus Verfasst am: 16. Nov 2020 17:21 Titel: Re: Verständnisfrage zu Dirac-Notation und Vektoren terminus Verfasst am: 16. Nov 2020 17:21 Titel: Re: Verständnisfrage zu Dirac-Notation und Vektoren |
 |
|
zu 1) ja, Erwartungswert schrieb ich ja auch, allerdings steht da im Text nur was von
σ =+1 oder <σ>=..., aber nichts von einem psi etc
- und warum man das ausgerechnet in < > schreibt, wird auch nicht erklärt.
zu 2) bitte keine Fremdwörter, ich habe keinen Schimmer, was ein Spinor ist ;-)
_________________
αΓγΔδεζηΘθικλµνΞξΠπϱΣστΦφχΨψΩω∫∂ħ⋅⟨⟩√≤≥∞∈ |
|
 |
terminus
Anmeldungsdatum: 17.10.2020
Beiträge: 555
|
 terminus Verfasst am: 17. Nov 2020 10:04 Titel: terminus Verfasst am: 17. Nov 2020 10:04 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
Bei (2) meinst du wohl
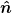
Das bezeichnet einen Einheitsvektor, z.B. im Ortsraum:
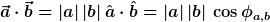
|
wo kommt in der unteren Multiplikations- Formel das 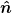 vor? vor?
_________________
αΓγΔδεζηΘθικλµνΞξΠπϱΣστΦφχΨψΩω∫∂ħ⋅⟨⟩√≤≥∞∈ |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 17. Nov 2020 10:54 Titel: TomS Verfasst am: 17. Nov 2020 10:54 Titel: |
 |
|
Ich hab‘ ganz allgemein a,b genommen. Muss ja nicht dein spezielles n = ein Spinvektor sein.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
terminus
Anmeldungsdatum: 17.10.2020
Beiträge: 555
|
 terminus Verfasst am: 17. Nov 2020 11:15 Titel: terminus Verfasst am: 17. Nov 2020 11:15 Titel: |
 |
|
ach so, nur allgemein a/b, ok, danke!
_________________
αΓγΔδεζηΘθικλµνΞξΠπϱΣστΦφχΨψΩω∫∂ħ⋅⟨⟩√≤≥∞∈ |
|
 |
terminus
Anmeldungsdatum: 17.10.2020
Beiträge: 555
|
 terminus Verfasst am: 19. Nov 2020 10:34 Titel: terminus Verfasst am: 19. Nov 2020 10:34 Titel: |
 |
|
warum man schreibt man denn nun <σ> für den Erwartungswert in spitze Klammern, hat das was mit den mit den Bra/Kets zu tun oder nicht?
_________________
αΓγΔδεζηΘθικλµνΞξΠπϱΣστΦφχΨψΩω∫∂ħ⋅⟨⟩√≤≥∞∈ |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 19. Nov 2020 10:39 Titel: TomS Verfasst am: 19. Nov 2020 10:39 Titel: |
 |
|
| terminus hat Folgendes geschrieben: | | warum man schreibt man denn nun <σ> für den Erwartungswert in spitze Klammern, hat das was mit den mit den Bra/Kets zu tun oder nicht? |
Ja, s.o.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
terminus
Anmeldungsdatum: 17.10.2020
Beiträge: 555
|
 terminus Verfasst am: 19. Nov 2020 10:59 Titel: terminus Verfasst am: 19. Nov 2020 10:59 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Ja, s.o. |
was genau steht denn dann in dem BraKet für ⟨σ⟩?
ist das nur eine Reelle Zahl oder ein Vektor (mit welchen Werten?) oder was sonst?
Ein Ket |A⟩ kann ich mir als n-dim Spalten-Vektor mit komplexen Zahlen als Komponenten vorstellen, ein Bra ⟨B| analog als Zeilenvektor, aber was ist ⟨σ⟩ ?
⟨σ⟩ = |n|⋅|m|⋅cos(φ) ist nach meinem Verständnis aber ja nur eine reelle Zahl, also warum dann in spitze Klammern schreiben?
_________________
αΓγΔδεζηΘθικλµνΞξΠπϱΣστΦφχΨψΩω∫∂ħ⋅⟨⟩√≤≥∞∈ |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 19. Nov 2020 13:15 Titel: TomS Verfasst am: 19. Nov 2020 13:15 Titel: |
 |
|
Zur Frage
| terminus hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Ja, s.o. |
was genau steht denn dann in dem BraKet für ⟨σ⟩? |
siehe hier:
| TomS hat Folgendes geschrieben: | 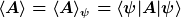
bezeichnet den Erwartungswert des Operators A im Zustand psi, wobei letzterer manchmal nicht notiert wird. |
| terminus hat Folgendes geschrieben: |
Ein Ket |A⟩ kann ich mir als n-dim Spalten-Vektor mit komplexen Zahlen als Komponenten vorstellen ... |
Nein, das ist letztlich falsch.
Ein Ket ist ein (abstrakter) Vektor, ein zugehöriger Spaltenvektor ist das N-Tupel der Komponenten dieses Vektors bzgl. einer Basis, d.h. die Projektion des Kets auf die Basis. Analog erhält man für einen (abstrakten) Operator eine Matrix.
Siehe zunächst mal hier:
https://www.physikerboard.de/topic,41973,-faq---dirac-notation-in-der-qm.html
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 19. Nov 2020 13:45 Titel: TomS Verfasst am: 19. Nov 2020 13:45 Titel: |
 |
|
Darf ich fragen, anhand welches Buches oder Skriptes du vorgehst?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
terminus
Anmeldungsdatum: 17.10.2020
Beiträge: 555
|
 terminus Verfasst am: 19. Nov 2020 13:57 Titel: terminus Verfasst am: 19. Nov 2020 13:57 Titel: |
 |
|
Zunächst bin ich kein Mathe- oder Physikstudent (habe etwas anderes studiert), und ich lese gerade 2 verschiedene Bücher:
L.Susskind, A.Friedman Quantenmechanik (Das theoretische Minimum) und
Steven Holzner Quantenmechanik (für dummies)
zu 1)
danke, aber das verstehe ich nicht:
was bedeutet in MEINEM obigen Beispiel
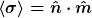
denn DEIN Zustand Psi in MEINEM Zusammenhang?
(ich verstehe ⟨σ⟩ als reelle Zahl aus ⟨σ⟩ = |n|⋅|m|⋅cos(φ), da erkenne ich kein Psi )
σ ist der gemessene Zustand längs 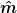 , im obigen Falle σ=+1. , im obigen Falle σ=+1.
zu 2)
das mit den "Projektionen" ist mir zu formal und zu abstrakt, auch in deinem Link.
Zumindest in meinen Lehrbüchern von Susskind/Friedmann und Holzner werden ebenfalls Bras |B> immer durch Zeilenvektoren mit den Komponenten
{b1, b2, b3,...}
und Kets |A> durch Spaltenvektoren
{a1
a2
a3
...}
dargestellt (alle a,b aus C).
PS,
es ist äußerst verwirrend, wenn du immer andere Buchstaben verwendest als ich, versuch doch bitte immer meine Symbolik zu verwenden...
_________________
αΓγΔδεζηΘθικλµνΞξΠπϱΣστΦφχΨψΩω∫∂ħ⋅⟨⟩√≤≥∞∈ |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 19. Nov 2020 14:31 Titel: TomS Verfasst am: 19. Nov 2020 14:31 Titel: |
 |
|
| terminus hat Folgendes geschrieben: | Zunächst bin ich kein Mathe- oder Physikstudent (habe etwas anderes studiert), und ich lese gerade 2 verschiedene Bücher:
L.Susskind, A.Friedman Quantenmechanik (Das theoretische Minimum) und
Steven Holzner Quantenmechanik (für dummies) |
s.u.
| terminus hat Folgendes geschrieben: |
zu 1)
danke, aber das verstehe ich nicht:
was bedeutet in MEINEM obigen Beispiel
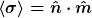
denn DEIN Zustand Psi in MEINEM Zusammenhang?
(ich verstehe ⟨σ⟩ als reelle Zahl aus ⟨σ⟩ = |n|⋅|m|⋅cos(φ), da erkenne ich kein Psi )
σ ist der gemessene Zustand, im obigen Falle σ=+1.
|
Das kann ich dir ohne den Kontext nicht sagen. Hast du eine Kopie?
| terminus hat Folgendes geschrieben: |
zu 2)
das mit den "Projektionen" ist mir zu formal und zu abstrakt, auch in deinem Link.
|
Stell dir einen Vektorpfeil vor; das ist der Ket. Nun führst du ein Koordinatensystem ein; die Komponenten bzgl. dieses Koordinatensystems bilden den Spaltenvektor. Wenn du ein anderes (rotiertes) Koordinatensystem verwendest, ändern sich die Koordinaten, nicht jedoch der Vektorpfeil selbst.
| terminus hat Folgendes geschrieben: |
Zumindest in meinen Lehrbüchern von Susskind/Friedmann und Holzner werden ebenfalls Bras |B> immer durch Zeilenvektoren und Kets |A> durch Spaltenvektoren dargestellt. |
Dann würde ich mir ernsthaft überlegen, andere Bücher zu verwenden. Insbs. bei Susskind irritiert mich das sehr.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
terminus
Anmeldungsdatum: 17.10.2020
Beiträge: 555
|
 terminus Verfasst am: 19. Nov 2020 14:34 Titel: terminus Verfasst am: 19. Nov 2020 14:34 Titel: |
 |
|
| Zitat: | | Das kann ich dir ohne den Kontext nicht sagen. Hast du eine Kopie? |
es gibt nur das, was ich oben zitiert habe, mehr steht nicht da!
| Zitat: | | Stell dir einen Vektorpfeil vor; das ist der Ket. Nun führst du ein Koordinatensystem ein; die Komponenten bzgl. dieses Koordinatensystems bilden den Spaltenvektor. Wenn du ein anderes (rotiertes) Koordinatensystem verwendest, ändern sich die Koordinaten, nicht jedoch der Vektorpfeil selbst. |
das ist klar, dass die Komponenten immer nur für die entspr. Vektorbasis gelten. Aber wenn man die hat, sind Bras Zeilenvektoren, und Kets Spaltenvektoren, wenn man damit rechnet (z.B. inneres Produkt)
_________________
αΓγΔδεζηΘθικλµνΞξΠπϱΣστΦφχΨψΩω∫∂ħ⋅⟨⟩√≤≥∞∈ |
|
 |
terminus
Anmeldungsdatum: 17.10.2020
Beiträge: 555
|
 terminus Verfasst am: 19. Nov 2020 16:32 Titel: terminus Verfasst am: 19. Nov 2020 16:32 Titel: |
 |
|
Vielleicht hat ja noch jemand anderes einen Erklärungsansatz:
Zitat:
| Zitat: | Beginnen wir mit einem längs 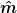 orientierten A (gemeint ist wohl der Ausrichtungsvektor einer Spin-Messapparatur) und bestätigen orientierten A (gemeint ist wohl der Ausrichtungsvektor einer Spin-Messapparatur) und bestätigen 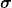 = +1, so ergeben nachfolgende Messungen mit A orientiert längs = +1, so ergeben nachfolgende Messungen mit A orientiert längs 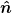 das statistische Resultat das statistische Resultat
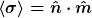 |
wenn 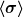 also ein statistisches Resultat ist, wieso schreibt man dann σ in spitze Klammern? also ein statistisches Resultat ist, wieso schreibt man dann σ in spitze Klammern?
Und was hat das mit Bra-Kets zu tun?
_________________
αΓγΔδεζηΘθικλµνΞξΠπϱΣστΦφχΨψΩω∫∂ħ⋅⟨⟩√≤≥∞∈ |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 19. Nov 2020 17:47 Titel: TomS Verfasst am: 19. Nov 2020 17:47 Titel: |
 |
|
| terminus hat Folgendes geschrieben: | | Zitat: | | Stell dir einen Vektorpfeil vor; das ist der Ket. Nun führst du ein Koordinatensystem ein; die Komponenten bzgl. dieses Koordinatensystems bilden den Spaltenvektor. Wenn du ein anderes (rotiertes) Koordinatensystem verwendest, ändern sich die Koordinaten, nicht jedoch der Vektorpfeil selbst. |
das ist klar, dass die Komponenten immer nur für die entspr. Vektorbasis gelten. Aber wenn man die hat, sind Bras Zeilenvektoren, und Kets Spaltenvektoren, wenn man damit rechnet (z.B. inneres Produkt) |
Also fangen wir von vorne an: du verstehst die Notation nicht; du verwendest ein Buch, das sie falsch erklärt; und du glaubst mir nicht ;-)
Solange wir den Knoten nicht durchschlagen, wird das nichts. Der rote Teil ist falsch.
1) Ein Vektor r im dreidimensionalen Raum hat eine Länge und eine Richtung. Er kann bzgl. einer Basis
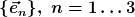
durch Komponenten r_n ausgedrückt werden:
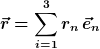
r ist der Vektor, r_n sind die Komponenten, und
_{n=1 \ldots 3})
ist der Spaltenvektor.
Du erhältst die Komponenten durch Projektion von r auf die Basis, d.h.
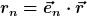
Also ist der Vektor nicht gleich dem Spaltenvektor, er repräsentiert ihn bezüglich einer bestimmten Basis.
2) In der Quantenmechanik wird der Zustand eines Systems durch einen Zustandsvektor in einem (im allgemeinen unendlich-dimensionalen) Vektorraum repräsentiert. Dieser Zustandsvektor ist der Ket, und er entspricht dem o.g. Vektor.
Nun kannst du den Zustandsvektor wieder auf einen Basis projizieren und erhältst das, was man in der Physik als Darstellung bezeichnet. Wenn du z.B. ein System betrachtest, das ausschließlich diskrete Energieniveaus hat, die mit n numeriert werden, dann folgt aus dem Zustandsvektor ein (unendlich-dimensionaler) Spaltenvektor.
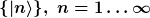
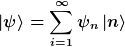
_{n=1 \ldots \infty})
3) Das Skalarprodukt zweier Vektoren entspricht dem Produkt der Länge mal dem Cosinus des Zwischenwinkels, d.h.
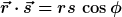
Es kann berechnet werden mittels der Komponenten
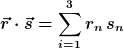
4) Solltest du bereits Wellenfunktionen begegnet sein, so gilt folgendes: man kann den o.g. Formalismus auf eine unendlich-dimensionale, kontinuierliche Basis erweitern; vieles ist dann mathematisch etwas tricky, aber das folgende gilt nach wie vor: durch Projektion auf die kontinuierliche Ortsbasis erhält man die Wellenfunktion, die sozusagen einem "kontinuierlichen Spaltenvektor" entspricht:
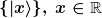
 \, |x\rangle)
 = \langle x | \psi \rangle)
Summen werden durch Integrale ersetzt.
Bzgl. des Bra-Ket-Formalismus ist das das theoretische Minimum - egal, was Susskind schreibt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
terminus
Anmeldungsdatum: 17.10.2020
Beiträge: 555
|
 terminus Verfasst am: 19. Nov 2020 18:09 Titel: terminus Verfasst am: 19. Nov 2020 18:09 Titel: |
 |
|
Leider hilft mir hier meine Schulmathematk nicht weiter: den Teil verstehe ich nicht ganz.
| Zitat: | Er kann bzgl. einer Basis
i) 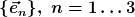
durch Komponenten 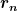 (richtig berichtigt?) ausgedrückt werden: (richtig berichtigt?) ausgedrückt werden:
ii) 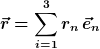
iii) r ist der Vektor, // <<<  oder oder 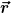 ?? ??
iv) 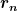 sind die Komponenten=Koeffizienten , und sind die Komponenten=Koeffizienten , und
v) _{n=1 \ldots 3}) ist der Spaltenvektor. ist der Spaltenvektor.
|
Einigen wir uns doch erstmal auf eine Standard-Orthonormalbasis, wie im R³.
Im R³ hat man die 3 Komponenten, die die Linearfaktoren der Raumrichtungen darstellen (x,y,z-Dimensionen)
i) bis iv) ist damit soweit verständlich.
v) ist unverständlich, für mich ist der Vektor als Spaltenvektor geschrieben dann
vi) 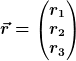 , ,
Damit wäre für mich vi) nichts anderes als die Koeffizienten des Vektors aus ii) und iv) in eine senkrechte Spalte = Spaltenvektor geschrieben.
Auch sonst schreibt man in der Mathematik ja Vektoren im R³ in Form ihrer 3 Komponenten innerhalb von Klammern (senkrecht oder waagerecht), s.a. hier:
https://de.wikipedia.org/wiki/Vektor#Darstellung_in_Koordinaten
Was
v) _{n=1 \ldots 3})
sein soll, erschließt sich mir nicht, diese Schreibweise sagt mir nichts...
(Weitere Fragen folgen nach Klärung dieses 1. Teils... ;-) )
(Der Forumseditor hier ist wirklich zum schreiend Davonlaufen, meine Herren... *kopfschüttel*)
_________________
αΓγΔδεζηΘθικλµνΞξΠπϱΣστΦφχΨψΩω∫∂ħ⋅⟨⟩√≤≥∞∈ |
|
 |
terminus
Anmeldungsdatum: 17.10.2020
Beiträge: 555
|
 terminus Verfasst am: 19. Nov 2020 18:55 Titel: terminus Verfasst am: 19. Nov 2020 18:55 Titel: |
 |
|
(edit, s.u.)
_________________
αΓγΔδεζηΘθικλµνΞξΠπϱΣστΦφχΨψΩω∫∂ħ⋅⟨⟩√≤≥∞∈
Zuletzt bearbeitet von terminus am 19. Nov 2020 19:26, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 19. Nov 2020 19:12 Titel: TomS Verfasst am: 19. Nov 2020 19:12 Titel: |
 |
|
_{n=1 \ldots 3} = \begin{pmatrix} r_1 \\ r_2 \\ r_3 \end{pmatrix}
<br />
)
A) Ein Vektor existiert, ohne dass irgendeine Basis definiert wurde und diesbzgl. Koordinaten berechnet wurden. Zeichne einen Pfeil auf ein Blatt weißes Papier, so hast du einen Vektor, noch ohne irgendwelche Koordinaten.
B) Es gibt nicht die Orthonormalbasis, sondern unendlich viele, die sich durch Drehungen unterscheiden.
Damit gilt
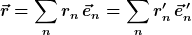
Da nun die Koordinaten und Basisvektoren untereinander verschieden sind, kann nicht ein und der selbe Vektor zwei verschiedenen Spaltenvektoren entsprechen.
 \neq (r^\prime_n) = \vec{r})
Wie soll das gehen?
C) Es gilt
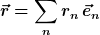
nicht jedoch
)
Das ist bereits formal etwas anderes.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 19. Nov 2020 19:16, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 19. Nov 2020 19:15 Titel: TomS Verfasst am: 19. Nov 2020 19:15 Titel: |
 |
|
Diese Schreibweise ist falsch.
Du kommst in der Schulmathematik damit klar, wenn du irrigerweise so denkst, in der Quantenmechanik bei Verwendung der Braket-Notation sicher nicht.
| terminus hat Folgendes geschrieben: | | nochmal meine Frage an alle anderen, irgendwie geht der vorige Post von TomS auch an meiner Frage vorbei ... |
Meine Antwort steht bereits da, aber du wirst sie nicht verstehen, solange du den Formalismus nicht verstehst (und solange ich raten muss, wie der Formalismus in deinen Büchern falsch angewandt wird)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
terminus
Anmeldungsdatum: 17.10.2020
Beiträge: 555
|
 terminus Verfasst am: 19. Nov 2020 19:22 Titel: terminus Verfasst am: 19. Nov 2020 19:22 Titel: |
 |
|
tja, das verstehe ich immer noch nicht. Auch in Wikipedia steht, wie ich es auch aus der Schule kenne:
[img]https://wikimedia.org/api/rest_v1/media/math/render/svg/e4f9cceb9bb69039065423d7fdfe2df69fa62799[/img]
hier ist auch der vektor GLEICH seiner Darstellung als Spaltenvektor
Und auch Susskind ist ja immerhin Professor, und auch er schreibt es so.
Sicher ist deine Schreibweise richtig, aber vielleicht ist sie auch einfach nur verüberkompliziert.
Didaktik ist aber ja auch die Kunst des Weglassens ;-)
_________________
αΓγΔδεζηΘθικλµνΞξΠπϱΣστΦφχΨψΩω∫∂ħ⋅⟨⟩√≤≥∞∈
Zuletzt bearbeitet von terminus am 19. Nov 2020 19:32, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 19. Nov 2020 19:25 Titel: TomS Verfasst am: 19. Nov 2020 19:25 Titel: |
 |
|
Ich habe jetzt ein paar Reviews zu den Büchern gelesen - im Falle von Susskind zur englischen Originalausgabe - und würde davon abraten.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
terminus
Anmeldungsdatum: 17.10.2020
Beiträge: 555
|
 terminus Verfasst am: 19. Nov 2020 19:27 Titel: terminus Verfasst am: 19. Nov 2020 19:27 Titel: |
 |
|
Steven Holzner macht es aber genau so.
_________________
αΓγΔδεζηΘθικλµνΞξΠπϱΣστΦφχΨψΩω∫∂ħ⋅⟨⟩√≤≥∞∈ |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 19. Nov 2020 19:28 Titel: TomS Verfasst am: 19. Nov 2020 19:28 Titel: |
 |
|
| terminus hat Folgendes geschrieben: | tja, das verstehe ich immer noch nicht. Auch in Wikipedia steht, wie ich es auch aus der Schule kenne:
[img]https://wikimedia.org/api/rest_v1/media/math/render/svg/e4f9cceb9bb69039065423d7fdfe2df69fa62799[/img]
bier ist auch der vektor GLEICH seiner Darstellung als Spaltenvektor
Und auch Susskind ist ja immerhin Professor, und auch er schreibt es so. |
Wenn das so ist, dann schreibt er es falsch.
| terminus hat Folgendes geschrieben: | tja, Sicher ist deine Schreibweise richtig, aber vielleicht ist sie auch einfach nur verüberkompliziert.
Didaktik ist aber ja auch die Kunst des Weglassens ;-) |
Die Schreibweise ist essentiell.
Bitte erkläre mir nicht, wie man Quantenmechanik erklärt! Mach einen Reset, verticke die Bücher und schau z.B. in die Feynman Lectures, die sollten frei verfügbar sein.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 19. Nov 2020 19:29, insgesamt einmal bearbeitet |
|
 |
terminus
Anmeldungsdatum: 17.10.2020
Beiträge: 555
|
 terminus Verfasst am: 19. Nov 2020 19:28 Titel: terminus Verfasst am: 19. Nov 2020 19:28 Titel: |
 |
|
(edit: englische Texte verstehe ich nicht, weder geschrieben noch gesprochen, und auch deutsche müssten populärwissenschaftlich verständlich sein)
also bitte nochmal mit der Bitte um eine einfache, verständliche Antwort an mich als Nicht-Physiker, um es zu verstehen, ohne Riesen-Universiätsmathematik-Overhead:
| Zitat: | | nochmal meine Frage an alle anderen, irgendwie geht der vorige Post von TomS auch an meiner Frage vorbei: |
| Zitat: | Beginnen wir mit einem längs 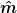 orientierten A (gemeint ist wohl der Ausrichtungsvektor einer Spin-Messapparatur) und bestätigen orientierten A (gemeint ist wohl der Ausrichtungsvektor einer Spin-Messapparatur) und bestätigen 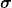 = +1, so ergeben nachfolgende Messungen mit A orientiert längs = +1, so ergeben nachfolgende Messungen mit A orientiert längs 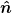 das statistische Resultat das statistische Resultat
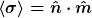 |
wenn 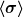 also ein statistisches Resultat ist (der Wert wird ja irgendwo im Intervall [-1;+1] ε R liegen) , wieso schreibt man dann σ in spitze Klammern? also ein statistisches Resultat ist (der Wert wird ja irgendwo im Intervall [-1;+1] ε R liegen) , wieso schreibt man dann σ in spitze Klammern?
Und was hat das mit Bra-Kets zu tun?
_________________
αΓγΔδεζηΘθικλµνΞξΠπϱΣστΦφχΨψΩω∫∂ħ⋅⟨⟩√≤≥∞∈ |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 19. Nov 2020 19:40 Titel: TomS Verfasst am: 19. Nov 2020 19:40 Titel: |
 |
|
| terminus hat Folgendes geschrieben: | | Steven Holzner macht es aber genau so. |
In der Quantenmechanik steht dann sowas da
 = \langle x|\psi\rangle)
Das ist Quatsch, aber das musst du mir nicht glauben und darfst gerne in die Irre gehen.
Ich verstehe nur nicht, warum du fragst, wenn dich die Antwort nicht interessiert.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
terminus
Anmeldungsdatum: 17.10.2020
Beiträge: 555
|
 terminus Verfasst am: 19. Nov 2020 19:43 Titel: terminus Verfasst am: 19. Nov 2020 19:43 Titel: |
 |
|
ich danke dir für deine Geduld, aber ich verstehe nicht, was du meinst oder erklären willst.
Vielleicht kann es daher bitte wirklich jemand anderes mal versuchen:
| Zitat: | Beginnen wir mit einem längs 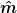 orientierten A (gemeint ist wohl der Ausrichtungsvektor einer Spin-Messapparatur) und bestätigen orientierten A (gemeint ist wohl der Ausrichtungsvektor einer Spin-Messapparatur) und bestätigen 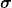 = +1, so ergeben nachfolgende Messungen mit A orientiert längs = +1, so ergeben nachfolgende Messungen mit A orientiert längs 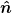 das statistische Resultat das statistische Resultat
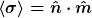
wenn 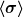 also ein statistisches Resultat ist (der Wert wird ja irgendwo im Intervall [-1;+1] ∈ R liegen) , wieso schreibt man dann σ in spitze Klammern? also ein statistisches Resultat ist (der Wert wird ja irgendwo im Intervall [-1;+1] ∈ R liegen) , wieso schreibt man dann σ in spitze Klammern? |
_________________
αΓγΔδεζηΘθικλµνΞξΠπϱΣστΦφχΨψΩω∫∂ħ⋅⟨⟩√≤≥∞∈ |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 19. Nov 2020 19:46 Titel: TomS Verfasst am: 19. Nov 2020 19:46 Titel: |
 |
|
| terminus hat Folgendes geschrieben: | | ich danke dir für deine Geduld, aber ich verstehe nicht, was du meinst oder erklären willst. |
Ich versuche dir die Notation für Bra und Ket zu erklären, die du nicht verstehst und auch nicht verstehen kannst - sowie alles daraus folgende - wenn sie in deinen Büchern falsch dargestellt wird.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
terminus
Anmeldungsdatum: 17.10.2020
Beiträge: 555
|
 terminus Verfasst am: 19. Nov 2020 19:52 Titel: terminus Verfasst am: 19. Nov 2020 19:52 Titel: |
 |
|
Mein Wissensstand:
Für mich ist Bra ein Vektor als Zeilenvektor und Ket ein Vektor als Spaltenvektor,
man multipliziert sie wie man üblicherweise n-dim Zeilenvektoren mit n-dim Spaltenvektoren multipliziert (komponentenweise Produkte addieren),
und so erhält man aus Bra mal Ket
<A| ⋅ |B> = <A|B>
Sind beide Vektoren über C^n (komplexe Komponenten), so ist das Braket ebenfalls eine komplexe Zahl (und eventuell sogar reell).
Man erhält aus einem Ket den korrespondierenden (transponierten) Bra, indem man ihn als Zeilenvektor schreibt und seine komplexen Komponenten durch deren komplex konjugierte ersetzt.
Das müsste doch nun richtig und hinreichend sein.
Das erklärt aber immer noch nicht meine Frage
| Zitat: | Beginnen wir mit einem längs 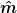 orientierten A (gemeint ist wohl der Ausrichtungsvektor einer Spin-Messapparatur) und bestätigen orientierten A (gemeint ist wohl der Ausrichtungsvektor einer Spin-Messapparatur) und bestätigen 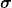 = +1, so ergeben nachfolgende Messungen mit A orientiert längs = +1, so ergeben nachfolgende Messungen mit A orientiert längs 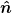 das statistische Resultat das statistische Resultat
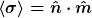
wenn 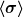 also ein statistisches Resultat ist (der Wert wird ja irgendwo im Intervall [-1;+1] ∈ R liegen) , wieso schreibt man dann σ in spitze Klammern? also ein statistisches Resultat ist (der Wert wird ja irgendwo im Intervall [-1;+1] ∈ R liegen) , wieso schreibt man dann σ in spitze Klammern? |
_________________
αΓγΔδεζηΘθικλµνΞξΠπϱΣστΦφχΨψΩω∫∂ħ⋅⟨⟩√≤≥∞∈ |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 19. Nov 2020 21:06 Titel: TomS Verfasst am: 19. Nov 2020 21:06 Titel: |
 |
|
| terminus hat Folgendes geschrieben: | Für mich ist Bra ein Vektor als Zeilenvektor und Ket ein Vektor als Spaltenvektor,
man multipliziert sie wie man üblicherweise n-dim Zeilenvektoren mit n-dim Spaltenvektoren multipliziert (komponentenweise Produkte addieren),
und so erhält man aus Bra mal Ket
<A| ⋅ |B> = <A|B> |
Ich wiederhole mich: das ist nicht korrekt.
Ein Ket wird dargestellt bzgl. einer Basis |n> mittels Komponenten a_n:
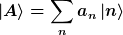
Die Multiplikation mittels Komponenten
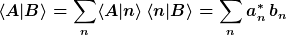
folgt mittels Projektion auf die Basis, d.h.
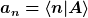
^\ast = \langle A|n\rangle )
Man erhält aus der Komponentendarstellung eines Ket’s die Komponentendarstellung des korrespondierenden Bra’s, indem man den Komponenten-Spaltenvektor als Zeilenvektor schreibt und komplex konjugiert.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 19. Nov 2020 21:12 Titel: TomS Verfasst am: 19. Nov 2020 21:12 Titel: |
 |
|
Hast du zu der weiteren Frage mehr Kontext? Eine Kopie der Seite?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
terminus
Anmeldungsdatum: 17.10.2020
Beiträge: 555
|
 terminus Verfasst am: 19. Nov 2020 22:05 Titel: terminus Verfasst am: 19. Nov 2020 22:05 Titel: |
 |
|
deine Formeln verstehe ich überwiegend nicht, aber ich sehe

exakt in Übereinstimmung mit meiner Beschreibung der Multiplikation:
"man multipliziert sie wie man üblicherweise n-dim Zeilenvektoren mit n-dim Spaltenvektoren multipliziert (komponentenweise Produkte addieren)...Man erhält aus einem Ket den korrespondierenden (transponierten) Bra, indem man ihn als Zeilenvektor schreibt und seine komplexen Komponenten durch deren komplex konjugierte ersetzt".
Außerdem verstehe ich darin auch keine Antwort auf meine Frage bezüglich <σ> (um die es mir eigentlich hier ausschließlich geht):
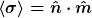
Eine Kopie der Seite habe ich nicht, aber ich habe sie quasi wortwörtlich zitiert, es steht alles da, was dort steht.
Das Einzige, was in dem Kapitel noch davor steht, ist:
"Die quantenmechanische Notation für den statistischen Mittelwert einer Größe Q ist Diracs Bracket-Notation <Q>", da müsste man also dann <Q> durch <σ>ersetzen, was aber jetzt auch nichts neues mehr ist.
Auch wird dadurch ja kein bißchen klarer, was nun ein statistischer Mittelwert OHNE BraKet-Klammern anderes ist als ein statistischer Mittelwert IN BraKet-Klammern (in BraKet Klammern stehen doch immer Vektoren oder Produkte von Vektoren), und was das ganze also soll.
_________________
αΓγΔδεζηΘθικλµνΞξΠπϱΣστΦφχΨψΩω∫∂ħ⋅⟨⟩√≤≥∞∈ |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 19. Nov 2020 22:31 Titel: TomS Verfasst am: 19. Nov 2020 22:31 Titel: |
 |
|
| terminus hat Folgendes geschrieben: | deine Formeln verstehe ich überwiegend nicht, aber ich sehe

exakt in Übereinstimmung mit meiner Beschreibung der Multiplikation:
"man multipliziert sie wie man üblicherweise n-dim Zeilenvektoren mit n-dim Spaltenvektoren multipliziert (komponentenweise Produkte addieren)". |
Das habe ich auch nie bestritten.
Zwei Vektoren werden multipliziert, indem man die Zeilen- und Spaltenvektoren der Komponenten multipliziert. Das bedeutet jedoch nicht, dass ein Vektor mit seinem Spaltenvektor identisch ist. Der Unterschied zwischen dem Ket und seinen Komponenten ist essentiell.
Wie kann es sein, dass das Buch Kets verwendet und du diesbzgl. Fragen stellst, du aber die Formeln nicht verstehst und nicht mal Fragen dazu stellst? Was tut dieses Buch eigentlich?
| terminus hat Folgendes geschrieben: | Außerdem verstehe ich darin auch keine Atwort auf meine Frage bezüglich <σ> (um die es mir eigentlich hier ausschließlich geht):
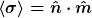
Eine Kopie der Seite habe ich nicht, aber ich habe sie quasi wortwörtlich zitiert, es steht alles da, was dort steht, und ich habe nichts weggelassen. |
Ja, aber da steht nicht, was A, m, n und sigma sein sollen; du bist dir ja selbst nicht sicher. Woher soll ich das wissen? Und warum soll ich dieser Darstellung vertrauen, wenn das Buch an anderer Stelle formal falsch ist?
Sorry, aber so kommen wir nicht weiter.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
terminus
Anmeldungsdatum: 17.10.2020
Beiträge: 555
|
 terminus Verfasst am: 19. Nov 2020 22:42 Titel: terminus Verfasst am: 19. Nov 2020 22:42 Titel: |
 |
|
m^ und n^ sind Einheitsvektoren, die im Winkel zueinander stehen und nach denen A (eine Apparatur zur Spinmessung) ausgerichtet wird, wie beschrieben wurde, das hatten wir auch schon besprochen.
Lies vlt nochmal den TO Post durch.
Auch habe ich ja bereits dargelegt, dass sowohl <A| (Zeilenvektor) als auch |B> (Spaltenvektor) als auch <A|B> (ihr Punktprodukt) beschrieben wurden, nicht aber dieses seltsame <σ> oder <Q>.
Also was soll das mathematisch sein, ein Mittelwert geschrieben in spitze Klammern, und warum spitze Klammern und was hat <Q> mit BraKets zu tun, da hier ja kein alleinstehender Vektor vorliegt und auch kein Bra mit einem Ket multipliziert wird?
_________________
αΓγΔδεζηΘθικλµνΞξΠπϱΣστΦφχΨψΩω∫∂ħ⋅⟨⟩√≤≥∞∈
Zuletzt bearbeitet von terminus am 19. Nov 2020 22:51, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 19. Nov 2020 22:51 Titel: TomS Verfasst am: 19. Nov 2020 22:51 Titel: |
 |
|
| terminus hat Folgendes geschrieben: | | m^ und n^ sind Vektoren, die im Winkel zueinander stehen und nach denen A ausgerichtet wird, wie beschrieben wurde, das hatten wir schon besprochen. |
Ja, aber was beschreiben sie physikalisch.
| terminus hat Folgendes geschrieben: | | Auch habe ich ja bereits dargelegt, dass sowohl |A> als auch |B> as auch <A|B> beschrieben wuren, nicht abber dieses seltsame <σ> oder <Q>. |
Ich habe oben geschrieben, dass wenn σ ein Operator ist, <σ> dessen Erwartungswert beschreibt. Wie kann es sein, dass du nicht weißt, welche Größe σ bezeichnet? Das muss in dem Buch doch diskutiert werden.
| terminus hat Folgendes geschrieben: | | Also was soll das mathematisch sein, ein Mittelwert geschrieben in spitze Klammern, und warum spitze Klammern und was hat <Q> mit BraKets zu tun, da hier ja kein alleinstejender vektor vorliegt und kein Bra mit einem Ket multipliziert wird? |
Wenn du endlich akzeptieren würdest, wie die Bra-Ket-Noration tatsächlich funktioniert - ich habe das mehrfach erklärt, dein Buch ja wohl nicht - dann könnte ich dir auch diese Fragen nochmal beantworten. Solange du dich aber dagegen sträubst und weiter an einem Buch festhältst, das dir offensichtlich nicht weiterhilft, weiß ich wirklich nicht, was ich dazu noch sagen soll.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
terminus
Anmeldungsdatum: 17.10.2020
Beiträge: 555
|
 terminus Verfasst am: 19. Nov 2020 22:55 Titel: terminus Verfasst am: 19. Nov 2020 22:55 Titel: |
 |
|
ich glaube, du hältst dich zu sehr an übergenauen Definitionen und spitzfindigen Definitionsfragen auf ohne die eigentliche Frage verstehen zu wollen.
Andererseits schreibst du ja selber
" wenn σ ein Operator ist, <σ> dessen Erwartungswert beschreibt"
Ja, WARUM zum Teufel schreibt man diesen Erwartungswert in spitze Klammern? Es ist doch wohl KEIN Vektor wie sonst Bras und Kets!
NUR DAS ist meine Frage!
(Außerdem sei angemerkt, dass du wieder nicht meine Beschreibung gelesen hast und dabei geblieben bist, denn bei mir ist σ kein Operator, sondern ein Messergebnis, aber sei's drum!)
_________________
αΓγΔδεζηΘθικλµνΞξΠπϱΣστΦφχΨψΩω∫∂ħ⋅⟨⟩√≤≥∞∈
Zuletzt bearbeitet von terminus am 20. Nov 2020 09:31, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 19. Nov 2020 23:47 Titel: TomS Verfasst am: 19. Nov 2020 23:47 Titel: |
 |
|
Deine Großschreibung macht‘s nicht besser.
Du fragst nach einer Definition bzw. Schreibweise und wirfst mir gleichzeitig vor, ich würde mich mit spitzfindigen Definitionen rumreiten? Ist das nicht etwas seltsam?
| TomS hat Folgendes geschrieben: |
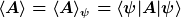
bezeichnet den Erwartungswert des Operators A im Zustand psi, wobei letzterer manchmal nicht notiert wird.
|
Es ist schlichtweg eine einprägsame Notation.
Ich habe deinen Text übrigens sehr wohl gelesen: „... so ergeben nachfolgende Messungen ... das statistische Resultat ...“ Es geht also nicht um ein Messergebnis, sondern m.M.m. um den Erwartungswert für diese Messungen.
Wenn man mehrere Systeme identisch präpariert und identische Messungen durchführt, erhält man über die Gesamtheit der einzelnen Messergebnisse einen Mittelwert. Mittels der Quantenmechanik kann man diesen berechnen, das entspricht gerade dem Erwartungswert. Welche Observable = messbare Größe man betrachtet, ist in dem Operator A codiert. Der Zustand, in dem die Systeme präpariert werden, ist in dem Ket codiert.
Mittelwert über N Messergebnisse:
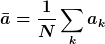
Berechneter Erwartungswert - und dabei schreibt man eben den Operator A:

Und natürlich gilt - wenn alles richtig funktioniert:

_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
terminus
Anmeldungsdatum: 17.10.2020
Beiträge: 555
|
 terminus Verfasst am: 20. Nov 2020 09:28 Titel: terminus Verfasst am: 20. Nov 2020 09:28 Titel: |
 |
|
danke, aber du antwortest wieder mit Dingen, nach denen ich nicht gefragt habe, verwendest meine Buchstaben anders als ich selber ( z.B. A in spitzen Klammern, wo doch bei mir A eine Messapparatur ist) und führst neue Buchstaben ein, die ich nicht verwendet habe und ohne sie zu erklären (wie deine zusätzlichen seltsamen Psis - ich habe so etwas nicht, was soll das sein?) (warum ist es so schwierig meine Buchstaben zu verwenden?) und sprichst auch noch von von neuen Begriffen wie "Operatoren", die ich nirgends in den Mund genommen habe.
Du verstehst offenbar meine Frage nicht, antwortest etwas anders mit völlig anderen Bezügen, Begriffen und Symbolen, und ich verstehe daher nicht deine Antwort: klassischer Fall von Aneinandervorbeireden. Wenn du also antwortest, bitte verwende NUR die Zeichen und Symbole und Bezeichner, so wie ich sie auch verwendet habe, sonst wird das nichts.
Vielleicht kann ja jemand anderes meine Fage beantworten.
wenn σ ein Messwert ist (für einen Spin längs einer Raumachse, also +1 oder -1), wieso verwendet man dann für seinen Erwartungswert ∈ [-1...+1] (Messung längs einer anderen (gekippten) Raumachse) die Schreibweise <σ>?
In diesem Falle ist es doch nur eine reelle Zahl, warum also nicht einfach den Erwartungswert schreiben, wie man es sonst tut (z.B. wie in der Stochastik als E(σ) ∈ R)?
Für was für eine "Struktur" (reelle Zahl, komplexe Zahl, Vektor, Matrix, Körper, Vektorraum...) steht diese Schreibweise stattdessen sonst im Allgemeinen, die mit ihren spitzen Klammern an die Schreibweise für Bra- oder Ket-Vektoren erinnert, aber ja wohl vielleicht (?) doch kein Vektor ist?
_________________
αΓγΔδεζηΘθικλµνΞξΠπϱΣστΦφχΨψΩω∫∂ħ⋅⟨⟩√≤≥∞∈ |
|
 |
|















