| Autor |
Nachricht |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2019
|
 Nils Hoppenstedt Verfasst am: 20. Nov 2020 12:10 Titel: Nils Hoppenstedt Verfasst am: 20. Nov 2020 12:10 Titel: |
 |
|
| terminus hat Folgendes geschrieben: |
Vielleicht kann ja jemand anderes meine Fage beantworten.
wenn σ ein Messwert ist (für einen Spin längs einer Raumachse, also +1 oder -1), wieso verwendet man dann für seinen Erwartungswert ∈ [-1...+1] (Messung längs einer anderen (gekippten) Raumachse) die Schreibweise <σ>?
|
Wie TomS schon sagte, das ist einfach nur eine übliche Schreibweise. Mir ist nicht ganz klar, warum du da so einen Zinnober darum veranstaltest. 
Viele Grüße,
Nils |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 20. Nov 2020 12:11 Titel: TomS Verfasst am: 20. Nov 2020 12:11 Titel: |
 |
|
| terminus hat Folgendes geschrieben: | | danke, aber du antwortest wieder mit Dingen, nach denen ich nicht gefragt habe ... |
Also zurück zur ursprünglichen Fragestellung:
| terminus hat Folgendes geschrieben: | Verständnisfrage zu Dirac-Notation und Vektoren
1.) ich kenne zwar die Schreibweisen |x> (Ket) und <y| (Bra) und <x|y> (BraKet), aber was genau ist 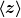 oder oder 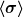 ? ? |
Ich antworte genau auf deine Frage und erkläre die Dirac-Notation.
| terminus hat Folgendes geschrieben: | | ... und führst neue Buchstaben ein, die ich nicht verwendet habe und ohne sie zu erklären (wie deine zusätzlichen seltsamen Psis - ich habe so etwas nicht, was soll das sein?) |
|.> ist ein Ket, egal, was du für den Punkt hinschreibst; x, n, psi, nlm, ... es ist immer ein Ket.
| terminus hat Folgendes geschrieben: | | ... und sprichst auch noch von von neuen Begriffen wie "Operatoren", die ich nirgends in den Mund genommen habe. |
Du liest ein Buch über Quantenmechanik, sagst, dir seien Kets vertraut, fragst nach der Bedeutung von 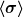 . Ich antworte dir, dass es sich um einen Erwartungswert eines Operators handelt. . Ich antworte dir, dass es sich um einen Erwartungswert eines Operators handelt.
Das Konzept ist jedenfalls essentiell; dafür, dass das Buch dies nicht erklärt, kann ich nichts.
Anstatt zu fragen, was ein Operator denn ist, wirfst du mir vor, dass ich es dir erklären möchte.
| terminus hat Folgendes geschrieben: | | Du verstehst offenbar meine Frage nicht, antwortest etwas anders mit völlig anderen Bezügen, Begriffen und Symbolen, und ich verstehe daher nicht deine Antwort: klassischer Fall von Aneinandervorbeireden. |
Ja - wobei ich da insbs. diesem Buch die Schuld gebe.
| terminus hat Folgendes geschrieben: | | Wenn du also antwortest, bitte verwende NUR die Zeichen und Symbole und Bezeichner, so wie ich sie auch verwendet habe, sonst wird das nichts. |
Also gut, letzter Versuch ...
| terminus hat Folgendes geschrieben: | | ... wenn σ ein Messwert ist (für einen Spin längs einer Raumachse, also +1 oder -1), wieso verwendet man dann für seinen Erwartungswert ∈ [-1...+1] (Messung längs einer anderen (gekippten) Raumachse) die Schreibweise <σ>? |
σ wird in deinem Fall leider in unterschiedlicher verwendet, ohne dass das Buch das erklärt.
Einmal ist σ ein Messwert: „bestätigen σ = +1“.
Einmal andermal ist σ eine Zufallsvariable im mathematischen Sinn: „so ergeben nachfolgende Messungen ... das statistische Resultat <σ>“; den Begriff der Zufallsvariable verwendet die Quantenmechanik jedoch nicht. Wichtig ist, dass es sich eben nicht um einen Messwert handelt, sondern um den Erwartungswert für viele Messungen.
Natürlich könnte man den Erwartungswert für σ als E(σ) bezeichnen. Aufgrund der Bra-Ket-Notation, ist es jedoch nach Dirac schlichtweg üblich und sinnvoll, stattdessen <σ> zu schreiben. Wenn du also die Quantenmechanik verstehen willst, dann vergiss E(σ) und verwende stattdessen <σ>.
Die Quantenmechanik spricht von messbaren Größen, sogenannten Observablen, z.B. Energie, Impuls, Drehimpuls, Spin, ... Diese Größen werden im Kontext von quantenmechanischen Systemen betrachtet, z.B. einem freien Elektron, einem Photon, einem Elektron im Atom, ...
In der Quantenmechanik werden diese Observablen mathematisch durch sogenannte Operatoren repräsentiert. Wenn nun in der Quantenmechanik die Schreibweise <σ> verwendet wird, dann bezeichnet σ einen solchen Operator - keine Zufallsvariable und keinen Messwert. Auch wenn du noch nicht weißt, was ein Operator ist, es ist keine Zahl (in der linearen Algebra wäre es eine Matrix - s.u.)
Und in der Quantenmechanik werden die zu betrachtenden Systeme durch Kets repräsentiert. Häufig schreibt man in den Ket irgendwas vernünftig rein, z.B. |0> für den Grundzustand, |n> für einen bestimmten Zustand, wenn die Zustände durch eine natürliche Zahl n angezählt werden können, |x> für einen Zustand an dem ein Teilchen einen präzisen Ort x einnimmt ...; oder |ψ> für einen beliebigen Zustand - vgl. x für eine beliebige Variable oder f(x) für eine beliebige Funktion.
Die Schreibweise <σ> bedeutet dann, dass im Zuge von Messungen an einem Ensemble identischer Systeme der Erwartungswert für die Observable σ gemeint ist (sollte dein Buch etwas anderes sagen, darfst du ihm misstrauen).
Die Schreibweise leitet sich von dem Bra-Ket-Formalismus ab, da für ein bestimmtest System, das durch den Ket |ψ> repräsentiert wird, die Berechnung des Erwartungswertes wie folgt funktioniert:

Der Erwartungswert der Observable σ für Messungen an Systemen repräsentiert durch Ket |ψ> berechnet sich zu = der rechte Ausdruck.
Diese Regel ist allgemeingültig für beliebige Observablen und beliebige quantenmechanisch Systeme - nicht nur für den Spin.
Wenn du die Darstellung des Kets

bzgl. einer Basis |n> kennst bzw. berechnen kannst, und wenn du die zugehörige Matrix-Darstellung des Operators σ berechnen kannst, dann funktioniert die Berechnung des Erwartungswertes <σ> anhand der Komponenten des Kets sowie der Komponenten der zugehörigen Matrix bzgl. der Basis |n> wie folgt:



Die Rechnung funktioniert - unter diesen Voraussetzungen - wie “Zeilenvektor mal Matrix mal Spaltenvektor”; der Operator wird in diesem Fall durch eine Matrix repräsentiert, i.A. jedoch nicht.
Wenn du dir einen Gefallen tun möchtest, dann arbeitest du dich an dieser Formel ab; danach hast du den Bra-Ket-Formalismus wirklich verstanden. Mathematische Voraussetzungen sind lineare Algebra, insbs. Vektoren und Matrizen, mehr nicht; Nachfragen sind möglich.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
terminus
Anmeldungsdatum: 17.10.2020
Beiträge: 555
|
 terminus Verfasst am: 20. Nov 2020 12:25 Titel: terminus Verfasst am: 20. Nov 2020 12:25 Titel: |
 |
|
nochmals vielen Dank für die Mühe, auch wenn ich nerve und auch wenn ich zu dumm bin, alles das zu verstehen.
Aber Schritt für Schritt:
| Zitat: | | Wie TomS schon sagte, das ist einfach nur eine übliche Schreibweise. Mir ist nicht ganz klar, warum du da so einen Zinnober darum veranstaltest |
| Zitat: | | Natürlich könnte man den Erwartungswert für σ als E(σ) bezeichnen. Aufgrund der Bra-Ket-Notation, ist es jedoch nach Dirac schlichtweg üblich und sinnvoll, stattdessen <σ> zu schreiben. Wenn du also die Quantenmechanik verstehen willst, dann vergiss E(σ) und verwende stattdessen <σ>. |
E(σ) ist aber eine reelle Zahl, dann wäre also <σ> auch eine reelle Zahl?
Glaube ich allerdings jetzt nicht mehr so recht, denn hier heißt es ja, es wäre eine Matrix - das ist nun allerdings (endlich) ein völlig neuer Aspekt:
| Zitat: | | Auch wenn du noch nicht weißt, was ein Operator ist, es ist keine Zahl (in der linearen Algebra wäre es eine Matrix - s.u.) |
Jetzt könnte sich allerdings das Dunkel lichten, denn mein <σ> wäre demnach keine reelle Zahl, sondern eine reelle 1x1 Matrix mit dem einzigen reellen Wert E(σ)?
(to be continued....)
_________________
αΓγΔδεζηΘθικλµνΞξΠπϱΣστΦφχΨψΩω∫∂ħ⋅⟨⟩√≤≥∞∈ |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 20. Nov 2020 12:52 Titel: TomS Verfasst am: 20. Nov 2020 12:52 Titel: |
 |
|
| terminus hat Folgendes geschrieben: | | Zitat: | | Natürlich könnte man den Erwartungswert für σ als E(σ) bezeichnen. Aufgrund der Bra-Ket-Notation, ist es jedoch nach Dirac schlichtweg üblich und sinnvoll, stattdessen <σ> zu schreiben. Wenn du also die Quantenmechanik verstehen willst, dann vergiss E(σ) und verwende stattdessen <σ>. |
E(σ) ist aber eine reelle Zahl, dann wäre also <σ> auch eine reelle Zahl? |
Natürlich ist das eine reelle Zahl, die Notation ändert doch nicht den Gehalt.
Spätestens aus der expliziten Berechnung ganz unten folgt (*), dass eine reelle Zahl vorliegt (dass es eine komplexe Zahl ist, ist offensichtlich, dass der Imaginärteil verschwindet, muss ich noch erklären)
| terminus hat Folgendes geschrieben: | | ... denn hier heißt es ja, es wäre eine Matrix - das ist nun allerdings (endlich) ein völlig neuer Aspekt: |
Du musst genau lesen, was ich schreibe: der Operator wäre eine Matrix, nicht jedoch der zugehörige Erwartungswert. Siehe die Berechnung ganz unten (*)
| terminus hat Folgendes geschrieben: | | ... denn mein <σ> wäre demnach keine reelle Zahl, sondern eine reelle 1x1 Matrix mit dem einzigen reellen Wert E(σ)? |
<σ> ist einfach eine reelle Zahl.
Zu den zwei Notationen
)
Genauso wie beim Ableiten
 = \frac{df(x)}{dx})
Zwei Notationen, die das selbe bedeuten.
(*)
| TomS hat Folgendes geschrieben: | 

 |
Darum geht es.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 20. Nov 2020 12:59, insgesamt einmal bearbeitet |
|
 |
terminus
Anmeldungsdatum: 17.10.2020
Beiträge: 555
|
 terminus Verfasst am: 20. Nov 2020 12:59 Titel: terminus Verfasst am: 20. Nov 2020 12:59 Titel: |
 |
|
ok, also doch eine reelle Zahl, danke. Das macht es einfacher, denn ich kann dann nach den Rechenregeln des Körpers der reellen Zahlen rechnen (und nicht nach den Rechenregeln des Vektorraums der Matrizen über dem Körper der reellen Zahlen ;-) )
Den Rest stelle ich mal kurz zurück...
Zurück also zunächst zu dem ominösen ψ, das bei dir immer auftaucht:
Wie wäre das ψ für mein Spin-Mess-Experiment explizit genau zu definieren?
Ich messe den Spin ja im R³, erst nach dem einen R³-Vektor ausgerichtet (wo ich σ=+1 messe, hätte ntl auch -1 sein können),
um dann anchließend nach Drehung der Messapparatur entlang eines anderen Raumvektors (um einen Winkel φ verdreht) - in Abhängigkeit von φ - den Erwartungswert <σ> zu berechnen?
(OMG, dieser Editor hier bringt mich um...!)
_________________
αΓγΔδεζηΘθικλµνΞξΠπϱΣστΦφχΨψΩω∫∂ħ⋅⟨⟩√≤≥∞∈ |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 20. Nov 2020 13:53 Titel: TomS Verfasst am: 20. Nov 2020 13:53 Titel: |
 |
|
| terminus hat Folgendes geschrieben: | | ok, also doch eine reelle Zahl, danke. Das macht es einfacher, denn ich kann dann nach den Rechenregeln des Körpers der reellen Zahlen rechnen (und nicht nach den Rechenregeln des Vektorraums der Matrizen über dem Körper der reellen Zahlen |
Vermutlich denkst du zu kompliziert.
| terminus hat Folgendes geschrieben: | Zurück also zunächst zu dem ominösen ψ, das bei dir immer auftaucht:
Wie wäre das ψ für mein Spin-Mess-Experiment explizit genau zu definieren?
Ich messe den Spin ja im R³, erst nach dem einen R³-Vektor ausgerichtet (wo ich +1 messe), und dann nach Drehung der Messapparatur entlang eines anderen Raumvektors, um einen Winkel φverdreht? |
Das können wir gerne tun, aber ich frage mich ernsthaft, was dein Buch nützt, wenn es das nicht erklärt.
Nochmal zurück zu
“Der Erwartungswert der Observable σ für Messungen an Systemen repräsentiert durch Ket |ψ> berechnet sich zu ...”
Der Zustand des Systems vor einer Messung wird repräsentiert durch einen Ket |ψ>; d.h. man muss unterscheiden, was über da System bekannt ist und was nicht bzw. was erst im Zuge einer Messung bekannt wird.
Betrachten wir ein Photon. Der Betrag des Spin ist s = 1. Die Orientierung des Spins vor der ersten Messung ist unbekannt. Nach der ersten Messung ist die Orientierung bekannt, nämlich +1.
Vorher:

Nachher:

Dabei bezeichnet s_z die Komponente des Spins parallel zu der Achse, bzgl. der gemessen wird. Vor der Messung ist dies unbekannt, das Photon befindet sich in einem Überlagerungszustand aus beiden möglichen Zuständen (bzgl. dieser Achse); die komplexen Koeffizienten a_+ und a_- sind unbekannt. Nach der Messung sind die Koeffizienten bekannt.
Der “Inhalt” des Kets, als das was zwischen | und > steht, kodiert sozusagen unser Wissen über das Photon.
Wenn man immer Photonen betrachtet, lässt man das “s = 1” weg und schreibt kurz
Vorher:

Nachher:

Das definiert die beiden Kets.
Die Wahrscheinlichkeit p, dass Spin-Orientierung +1 bzw. -1 gemessen werden wird, lautet

Dies kann auch als Erwartungswert von Operatoren E geschrieben werden:


Zu Details der Algebra später.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
terminus
Anmeldungsdatum: 17.10.2020
Beiträge: 555
|
 terminus Verfasst am: 20. Nov 2020 14:05 Titel: terminus Verfasst am: 20. Nov 2020 14:05 Titel: |
 |
|
dein s, ist das mein σ?
_________________
αΓγΔδεζηΘθικλµνΞξΠπϱΣστΦφχΨψΩω∫∂ħ⋅⟨⟩√≤≥∞∈ |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 20. Nov 2020 14:20 Titel: TomS Verfasst am: 20. Nov 2020 14:20 Titel: |
 |
|
Nein ;-)
Dein σ = +1 bezeichnet einen Messwert.
Dein <σ> bezeichnet den Erwartungswert für die Messungen der Observablen bzw. des Operators σ.
Mein s=1, s_z = * bezeichnet den Zustand des Photons.
Vor der Messung ist s_z = * unbekannt. Im Zuge der Messung erhältst du zufällig einen Messwert, z.B. σ = +1. Dadurch ändert sich der Zustand des Photons zu s_z = +1.
Du musst Messwert und Zustand auseinanderhalten, das ist sowohl mathematisch als auch physikalisch etwas anderes.
Steht davon nichts in deinem Buch? Messprozess, Kollaps oder Reduktion, Projektion, Eigenwerte und Messwerte, Bornsche Regel, ...?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
terminus
Anmeldungsdatum: 17.10.2020
Beiträge: 555
|
 terminus Verfasst am: 20. Nov 2020 14:42 Titel: terminus Verfasst am: 20. Nov 2020 14:42 Titel: |
 |
|
bis jetzt bin ich erst nur bis S. 27 gekommen, und da wurde noch kein Psi gebraucht und kein Operator eingeführt, ich versuche daher erst einmal nur das <σ> zu verstehen, samt Rechenregeln.
(Denn tatsächlich rechnet man ja mit Vektoren oder Matrizen untereinander anders als mit Zahlen untereinander).
Rest kommt sicher noch, es sind ja immerhin noch über 200 Seiten.
Zwischenstand bisher (IIUC):
<σ> ist kein Bra, kein Ket und kein BraKet, sondern nur eine einfache reelle Zahl,
die beidseitigen "Pfeilrichtungen" der Klammern bei <σ> haben nichts mit den Pfeilrichtungen der Klammern bei |x> und <y| oder <y|x> zu tun,
und daher ist es nur eine ungewohnte Schreibweise für eine einfache reelle Zahl
- und es hat vor allem nichts direkt mit den Bra/Kets zu tun (außer dass man es beim Rechnen auch mit BraKets verwendet) - das hatte ich beim Post vom 19. Nov 2020 10:39 offenbar missverstanden.
Also,
bislang sind sowohl Operatoren als auch das ψ, so wie du es verwendest, komplettes Neuland. Kommt aber vlt schon bald auch im Buch, mal schaun...
Was mich noch verwirrt, ist die Schreibweise für einen Ket (oder Bra)

Nachher:

denn ich verstand einen Ket oder Bra jew. als Vektor eines Vektorraums -
um was für einen Vektorraum handelt es sich aber hier, mit wieviel Dimensionen, über welchem Körper ( R^n oder C^n , n=?? )?
Ist es ein C², und |ψ> folglich ein 2-dim Vektor mit komplexen Komponenten?
Und haben die |ψ> immer diese Dimension, oder ist die Dimension beliebig, ggf sogar ∞?
_________________
αΓγΔδεζηΘθικλµνΞξΠπϱΣστΦφχΨψΩω∫∂ħ⋅⟨⟩√≤≥∞∈ |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 20. Nov 2020 15:27 Titel: TomS Verfasst am: 20. Nov 2020 15:27 Titel: |
 |
|
Die Notation mit Bra und Ket abstrahiert davon, um welchen Vektorraum es sich handelt; deswegen ist sie oft sehr kompakt und praktisch für allgemeine Überlegungen.
Für konkrete Berechnung nutzt man dann z.B. Spaltenvektoren - s.u.
1) Für ein Spin-System mit zwei möglichen Ausrichtungen ist der Vektorraum zweidimensional; dies ist der Fall für Spin-1/2 Teilchen wie z.B. Elektronen sowie masselose Teilchen wie insbs. Photonen. Die o.g. Zustände

bilden eine Basis.
Für die Dimension bei Spin

gilt (mit Ausnahme der masselosen Teilchen mit dim = 2)

I.A. liegt in der Quantenmechanik jedoch ein unendlich-dimensionaler Hilbertraum vor.
2) Im Falle einer diskreten Basis gehören die Komponenten-Vektoren dem speziellen l²-Folgenraum an, d.h. einer Verallgemeinerung endlich-dimensionaler Spaltenvektoren.
3) In vielen Fällen verwendet man jedoch auch den unendlich-dimensionalen L²-Funktionenraum.
Bsp.:
Betrachte Funktionen f(x) mit Fourierreihen
 = \sum_{k=-\infty}^{+\infty} f_k \, e^{ikx})
Die Koeffizienten bilden einen unendlich-dimensionalen Spaltenvektoren im l².
Die Funktionen selbst sind Elemente des L². Die Formel stellt eine Entwicklung von f(x) nach einer Basis dar, den Exponentialfunktionen in der Fourierreihe.
4) Nun sind alle separablen Hilberträume isometrisch isomorph, d.h. es ist letztlich egal, welchen man nutzt, da man sie bijektiv aufeinander abbilden kann. Deswegen abstrahiert man von Darstellungen wie (2) oder (3) und schreibt allgemein den Ket |f>. (2) und (3) sind dann nur spezielle Darstellungen für |f>.
Physikalisches Beispiel: Betrachte Schwingungen eines kreisförmigen Haushaltsgummies. Es seien die Grundschwingung sowie die dritte Oberschwingung angeregt.
(2)
Folge
 = (f_0, 0, 0, f_3, 0, \ldots))
Skalarprodukt zweier Folgen f,g

(3)
Funktion
 = f_0 + f_3 \, e^{3ix})
Skalarprodukt zweier Funktionen (bis auf Normierung sowie die Länge des Gummies)
 \, g(x))
(4)
Bra-Ket

Skalarprodukt

https://de.m.wikipedia.org/wiki/Hilbertraum
https://de.m.wikipedia.org/wiki/Folgenraum
https://de.m.wikipedia.org/wiki/Lp-Raum#Der_Hilbertraum_L2
https://de.m.wikipedia.org/wiki/Isometrische_Isomorphie
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 20. Nov 2020 15:45, insgesamt 3-mal bearbeitet |
|
 |
terminus
Anmeldungsdatum: 17.10.2020
Beiträge: 555
|
 terminus Verfasst am: 20. Nov 2020 15:38 Titel: terminus Verfasst am: 20. Nov 2020 15:38 Titel: |
 |
|
ok, danke, noch sehr viel Mathematik, die ich komplett noch nicht verstehe, aber was nicht ist,....
verstehe ich es aber dann richtig, nachdem der Vekrorraum der |ψ> hier offenbar aufgespannt wird durch { |+1>, |-1> }, was ja beides anscheinend reelle Einheitsvektoren sind, also dann
|ψ> ∈ R²
ist?
_________________
αΓγΔδεζηΘθικλµνΞξΠπϱΣστΦφχΨψΩω∫∂ħ⋅⟨⟩√≤≥∞∈ |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 20. Nov 2020 15:58 Titel: TomS Verfasst am: 20. Nov 2020 15:58 Titel: |
 |
|
| terminus hat Folgendes geschrieben: | verstehe ich es aber dann richtig, nachdem der Vekrorraum der |ψ> hier offenbar aufgespannt wird durch { |+1>, |-1> }, was ja beides anscheinend reelle Einheitsvektoren sind, also dann
|ψ> ∈ R²
ist? |
Fast.
Zunächst mal sind die Koeffizienten komplex, d.h. es liegt ein 2-dim. Vektorraum über den komplexen Zahlen vor.
Aber (!)

sondern


Der Ket selbst ist nur ein abstraktes Symbol, ein Element eines abstrakten Hilbertraumes.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
terminus
Anmeldungsdatum: 17.10.2020
Beiträge: 555
|
 terminus Verfasst am: 20. Nov 2020 16:17 Titel: terminus Verfasst am: 20. Nov 2020 16:17 Titel: |
 |
|
hm, ok, verstehe ich jetzt allerdings nicht um ehrlich zu sein. Muss aber sicher auch noch nicht sein.
An dieser Stelle im Buch ist sicher auch erst mal nur wichtig, dass nach der Drehung von A von m^ um z.B. 45° nach n^ dann der Erwartungswert
<σ> = |m^| |n^| cos(45°) = 0,70711 ist. (uups, erst verrechnet)
Falls dann hier irgendwann mal das Psi dazu kommt, werde ich intensivst vorbereitet sein, vielen herzlichen Dank! 8-)
_________________
αΓγΔδεζηΘθικλµνΞξΠπϱΣστΦφχΨψΩω∫∂ħ⋅⟨⟩√≤≥∞∈
Zuletzt bearbeitet von terminus am 20. Nov 2020 16:21, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 20. Nov 2020 16:20 Titel: TomS Verfasst am: 20. Nov 2020 16:20 Titel: |
 |
|
Mal ein Beispiel, damit du verstehst, dass Kets keine Spaltenvektoren sind.
Wir betrachten das Wasserstoffatom - genauer ein Elektron im Wasserstoffatom. Der Kürze halber lassen wir den Spin des Elektrons weg.
Das Elektron kann sich in Zuständen befinden, die mit n,l,m bezeichnet werden; n ist die Hauptquantenzahl, l steht für den Bahndrehimpuls und m für dessen z-Komponente.
Durch Lösen der quantenmechanischen Gleichungen findet man die erlaubten Werte


, \ldots, l-1, l)
Wenn z.B. n = 3, dann ist l =2 der maximal erlaubte Wert, und m läuft über -2,-1,0,1,2.
Ein erlaubter Zustand wäre also gegeben durch n = 3 , l = 1, m = -1.
Der Physiker schreibt dafür kurz

Dies ist kein Vektor im R^3, einfach ein Symbol!
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
terminus
Anmeldungsdatum: 17.10.2020
Beiträge: 555
|
 terminus Verfasst am: 20. Nov 2020 16:23 Titel: terminus Verfasst am: 20. Nov 2020 16:23 Titel: |
 |
|
danke, das lasse ich jetzt mal so stehen und sacken... ;-)
_________________
αΓγΔδεζηΘθικλµνΞξΠπϱΣστΦφχΨψΩω∫∂ħ⋅⟨⟩√≤≥∞∈ |
|
 |
|
|
















