| Autor |
Nachricht |
lena18
Anmeldungsdatum: 11.10.2009
Beiträge: 464
|
 lena18 Verfasst am: 11. Okt 2009 21:10 Titel: Hebel mit Gegengewicht |
 |
|
Hallo
Ich habe leider keinen Ansatz für folgende Aufgabe:
Ich hoffe mir kann jemand dabei helfen.
Eine gewichtslos angenommene Stange mit FG am Ende liegt bei B auf einer reibungslosen Rolle und stützt sich bei A gegen die Wand ab. Wie groß muss der Reibwinkel in A sein, wenn Gleichgewicht herrschen soll?
Alfa 30°
von Lager A bis B l/2 von B zu FG l/2 (schräge gemessen)
Wie geht man da vor?
vielen dank im Voraus
lena
|
|
 |
xkris
Anmeldungsdatum: 06.10.2005
Beiträge: 281
Wohnort: LÜbeck
|
| xkris Verfasst am: 11. Okt 2009 21:41 Titel: |
|
|
Wie wärs mit einer Skizze? Macht die Sache für alle Beteiligten einfacher 
|
|
|
Gajeryis
Anmeldungsdatum: 08.10.2009
Beiträge: 194
Wohnort: CH - Bern
|
| Gajeryis Verfasst am: 11. Okt 2009 21:57 Titel: |
|
|
Ich denke, ich nehme korrekt an, dass der Punkt A, wo der Stab an die vertikale Wand drückt, am tiefsten liegt, der Stab dann um alpha = 30° gegenüber der Horizontalen geneigt nach oben verläuft? Auf halber Stablänge ist er rollreibungsfrei aufgelagert, ganz oben ist das freie Ende, wo die Kraft F_G senkrecht nach unten einwirkt.
Stelle mal eine Liste auf, welche Kräfte alle am Stab angreifen und in welche Richtung sie wirken: horizontal, vertikal, in Stabrichtung, senkrecht zur Stabrichtung.
Dann überleg dir, wie du die Kräfte schrittweise durch eine Funktion von F_G ausdrücken kannst. Du wirst Punkte finden, an denen du Gleichgewichtsbedingungen aufstellen kannst.
Mit Gleichgewichtsbedingungen meine ich zum Beispiel das Gleichgewicht von Kräften in eine bestimmte Richtung, oder das Gleichgewicht von Momenten um einen Punkt.
|
|
|
lena18
Anmeldungsdatum: 11.10.2009
Beiträge: 464
|
| lena18 Verfasst am: 11. Okt 2009 22:07 Titel: |
|
|
Hallo
hey danke für eure Antworten.
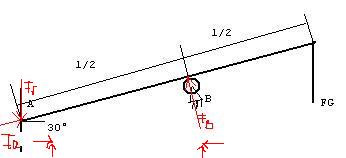
War ein Bisschen umständlich, aber ch habe mal eine Skizze gemacht.
Ich hoffe sie reicht aus.
die Kräfte habe ich mal eingetragen
was mache ich jetzt?
vielen Dank
lena
| Beschreibung: |
|
| Dateigröße: |
7.81 KB |
| Angeschaut: |
17289 mal |
|
|
|
|
Gajeryis
Anmeldungsdatum: 08.10.2009
Beiträge: 194
Wohnort: CH - Bern
|
| Gajeryis Verfasst am: 11. Okt 2009 23:32 Titel: |
|
|
Ok... Die Skizze sieht schon mal nicht schlecht aus (vom graphischen Standpunkt abgesehen ). Der Stab ist vorhanden, die Wand ist erkennbar, Kräfte sind vorhanden, Längen- und Winkelbemassungen sind vorhanden, sehr schön.
Was mir gerade auffällt: Wenn ich das richtig sehe (und die Indizes richtig entziffere), hast du die Kräfte bei Punkt A wie folgt eingezeichnet: F_r senkrecht nach unten; F_R in Stabrichtung zum Stab hin.
Das ist nicht falsch. Du wirst aber sehen, dass du die Kräfte sinnvoller hättest einzeichnen können. Sehen wir uns an, was für Kräfte im Punkt A wirken:
Der Stab berührt bei Punkt A die Wand. Da der Stab nicht abrutschen soll, muss eine Reibungskraft entlang der Wand wirken. Du hast diese korrekt eingezeichnet. Damit aber Reibung wirken kann, muss eine Kontaktkraft zwischen Stab und Wand wirken, die Normalkraft. Eins: Eine Normalkraft wirkt wie der Name sagt normal, sprich senkrecht, auf die Fläche, welche die Normalkraft bewirkt; das wäre hier die vertikale Wand. Zwei: Damit du diese Kontaktkraft möglichst einfach mit der Reibungskraft in Beziehung stellen kannst, sollten Reibungs- und Normalkraft senkrecht aufeinander stehen. Dann gilt nämlich die (dir sicher bekannte) Beziehung:
mit my als Reibungsbeiwert bzw. phi als Reibungswinkel.
Wenn du die Kraft F_R aber in Stabrichtung einführst - wie in deiner Skizze -, dann setzt sich die vertikale Kraft, welche den Stab an Ort hält, aus der Reibungskraft F_r und -sin(alpha)*F_R zusammen. Das verkompliziert zukünftige Rechnungen nur.
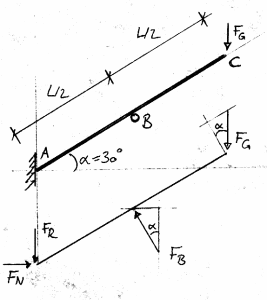
Nun, wie gesagt, deine Skizze ist nicht falsch und du solltest zum selben Resultat kommen. Aber wir wollen es dir ja möglichst einfach machen. Ich habe dir deshalb eine Handskizze von mir angehängt. Mit dieser solltest du gut zurechtkommen.
Ok. Die einzige bekannte Kraft ist zur Zeit F_G.
Jetzt geht es darum, die anderen Kräfte in Abhängigkeit von F_G zu bestimmen. Eine "korrekte" Reihenfolge gibt es da nicht.
Eine gute Möglichkeit ist z.B., mit F_B zu beginnen. Grund: Du hast zwei unbekannte Kräfte, welche in A angreifen. Wenn du nun die Hebelkräfte (=Momente) um den Punkt A anschaust, spielen F_R und F_N keine Rolle (durch die Hebellänge null tragen sie nichts zu den Momenten um A bei). Dadurch hast du für das Gesamtmoment um A nur noch F_G und F_B, eine Gleichung, eine Unbekannte.
Danach kannst du F_N aus den horizontal wirkenden Kräften rechnen.
Zum Schluss noch F_R aus den vertikal wirkenden Kräften.
Da nun die oben genannte Beziehung zwischen F_N und F_R wirken muss, kannst du my bzw. phi als Funktion von alpha bestimmen.
Wenn du magst, kannst du dein Ergebnis und vielleicht gar auch die Zwischenschritte hier reinstellen, damit wir sehen, ob die Lösung der Aufgabe geklappt hat, oder ob noch Hilfebedarf besteht.
| Beschreibung: |
|
| Dateigröße: |
9.06 KB |
| Angeschaut: |
17272 mal |
|
|
|
|
lena18
Anmeldungsdatum: 11.10.2009
Beiträge: 464
|
| lena18 Verfasst am: 12. Okt 2009 21:51 Titel: |
|
|
Hallo Gajeryis
Vielen Dank für deine Antwort, hat mir sehr geholfen, vor allem, weil du es genau erklärt hast.
also ich habe mal gerechnet: (kenn mich leider nicht aus mit latex, ist mir leider zu kompliziert)
cosa=FBY/FB
sina=FBx/FB
cosa=FGy/FG
sina=FGx/FG
Summe x muss dann
FN-FBx -> FN=FBx
Summe y
FR+FG-FBy
Summe M
-FB*l/2 + FGy*2*l/2
FGy=FB2=FG*cosa
FB=2 FG cosa
FR=FN.tanro=FBx.tanro
FR=FBy-FG
FR muss FR sein
FBx.tanro= FBy-FG
FB*sina*tanro= cosa*FB-FG
2FGcosa*sina*tanro= 2FG*cos²a-FG
tanro=2*cos²a-1/2cosa*sina=0,5774
ro= arctan 0,5774=30°
vielen vielen dank, aber warum wieder 30°?
lena
|
|
|
Gajeryis
Anmeldungsdatum: 08.10.2009
Beiträge: 194
Wohnort: CH - Bern
|
| Gajeryis Verfasst am: 13. Okt 2009 00:08 Titel: |
|
|
Hat ja prima geklappt, gut gemacht.
Noch eine Anmerkung:
| lena18 hat Folgendes geschrieben: | cosa=FGy/FG
sina=FGx/FG |
Gefährlich, die Komponenten längs und quer zum Stab auch mit x und y zu bezeichnen.
So wie du im Absatz darüber x und y eingeführt hast, wäre FGx = 0, FGy = -FG. x und y sind Achsen eines von dir festgelegten Koordinatensystems.
Gib beim nächsten Mal mehr Acht auf die Bezeichnungen. Am besten ist natürlich, wenn du die Achsen des Koordinatensystems gleich mit entsprechend beschrifteten Pfeilen der Skizze hinzufügst. Dann hast du die positive Richtung der Achsen gleich festgelegt und vermeidest Vorzeichenfehler beim Aufstellen der Gleichungen.
In diesem Fall hättest du vier Achsen einführen können: x für horizontal, y für vertikal, u für längs des Stabes, v für quer.
Wie gesagt, du hast die Aufgabe richtig gelöst und zum Glück horizontal/vertikal-x/y nicht mit längs/quer-x/y vermischt... trotzdem aufpassen.
| Zitat: | | aber warum wieder 30°? |
Man möchte fast sagen "Zufall". Ich hab mir die Funktion phi = f(alpha) mal angesehen und in Grad ausgedrückt lässt sie sich wie folgt vereinfachen:
Bei alpha = 30° ist da nun auch phi = 30°.
Was du an dieser Gleichung auch siehst, ist, dass bei einem Winkel von 45° gar keine Reibung nötig ist, die Normalkraft sowie das Lager halten den Stab stabil.
Sobald 45° überschritten wird, wirkt die Reibungskraft entgegengesetzt, der Reibungswinkel muss wieder zunehmen.
|
|
|
lena18
Anmeldungsdatum: 11.10.2009
Beiträge: 464
|
| lena18 Verfasst am: 13. Okt 2009 20:32 Titel: |
|
|
Hallo
Ich danke dir zuerst für deine Hilfe.
Wir haben noch so ein Beispiel bekommen und ich kriegs einfach nicht hin.
Habs sogar so gemacht wie du.
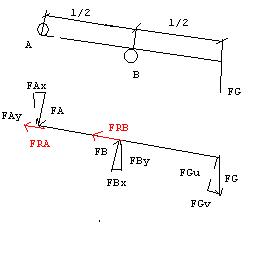
Eine gewichtslos angenommene Stange mit dem Gewicht FG am Ende ist zwischen zwei Sprossen A und B gesteckt. Der Reibungskoeffizient beträgt bei a und B jeweils 0,33. Unter welchem Winkel kann das System maximal geneigt werden, ohne dass die Stange herunterrutscht.
FAx-FBx -> FAx=FBx
FAy-FBy+FG
FA*cosa-FB*cosa+FG
FA=(FB*cosa-FG)/cosa
FGu*l-FB*(l/2)
FB=2FGu*l/l = 2FGu= 2*FG*cosa
FRA+FRB-FGv
(FA+FB)*müy=FG*sina
[(FB*cosa-FG)/cosa+FB]*müy=FG*sina
[(2FG*cosa*cosa-FG)/cosa+2FG*cosa]*müy=FG*sina
[(2*cosa-1/cosa+2*cosa]*müy=sina
[(4*cosa-1/cosa]*müy=sina
4*cosa*cosa-1=sina*cosa/müy
 wie rechnet man denn den Winkel aus?
Ausserdem haben wir vom Lehrer eine neue Aufgabe bekommen, sie sei leichter als das erste Beispiel. Für mich aber ist die Aufgabe alles andere als leicht. Ich habe keine Ahnung. Kann mir jemand helfen?
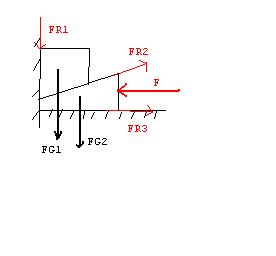
Mit Hilfe eines Keiles soll ein Block mit FG=15000N gehoben werden. Der Reibwinkel wird für alle Flächen auf 10° geschätzt. Welche Kraft brauchen Sie, um den Block in Bewegung zu setzen? die Keilgesichtskraft beträgt 200N. Alfa des Keiles 5°
Hinweis: Gewichtskraft des Klotzes wirkt über vertikale Kante des Keiles.
Ich weiss nicht wie ich anfangen soll, kann mir bitte jemand helfen?
Skizzen habe ich dieses Mal gleich angehängt.
Danke vielmasl
lena
| Beschreibung: |
|
| Dateigröße: |
8.49 KB |
| Angeschaut: |
17194 mal |
|
| Beschreibung: |
|
| Dateigröße: |
5.85 KB |
| Angeschaut: |
17194 mal |
|
|
|
|
Gajeryis
Anmeldungsdatum: 08.10.2009
Beiträge: 194
Wohnort: CH - Bern
|
| Gajeryis Verfasst am: 14. Okt 2009 12:39 Titel: |
|
|
| lena18 hat Folgendes geschrieben: | | Eine gewichtslos angenommene Stange mit dem Gewicht FG am Ende ist zwischen zwei Sprossen A und B gesteckt. Der Reibungskoeffizient beträgt bei a und B jeweils 0,33. Unter welchem Winkel kann das System maximal geneigt werden, ohne dass die Stange herunterrutscht. |
Ok. Du hast in deinen ersten Gleichungen schon Fehler:
| Zitat: | FAx-FBx -> FAx=FBx
FAy-FBy+FG |
Wo sind die Reibungskräfte? Die haben auch x- und y-Anteile.
Zudem brauchst du so, wie du das Koordinatensystem eingeführt hast, sehr viele sinus- und cosinus-Anhängsel. Wenn du dir den Stab anschaust, greift nur die Kraft FG schräg an. Die Reibungskräfte greifen längs an, die Sprossenkräfte senkrecht zum Stab. Du vereinfachst dir die Gleichung, wenn du das Koordinatensystem dem Stab entlang wählst. So brauchst du cosinus und sinus nur, um FG in die Komponenten quer und längs zum Stab aufzuteilen.
Du wirst sehen, diese Aufgabe ist ziemlich leicht.
Nächste Aufgabe:
| Zitat: | Mit Hilfe eines Keiles soll ein Block mit FG=15000N gehoben werden. Der Reibwinkel wird für alle Flächen auf 10° geschätzt. Welche Kraft brauchen Sie, um den Block in Bewegung zu setzen? die Keilgesichtskraft beträgt 200N. Alfa des Keiles 5°
Hinweis: Gewichtskraft des Klotzes wirkt über vertikale Kante des Keiles. |
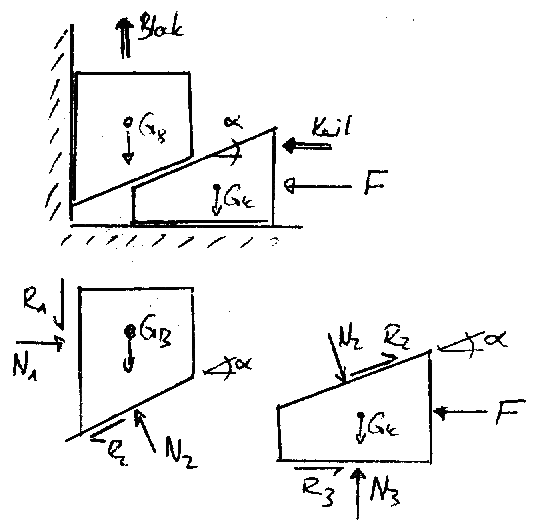
Für diese Aufgabe lohnt es sich, bei der Skizze die beiden Körper auseinanderzunehmen. Denn du hast auch Kontakt- und Reibungskräfte zwischen Block und Keil. Ich hänge dir meine Skizze an.
Das gibt für beide Körper je eine Gleichung für die Horizontale und für die Vertikale.
Ich habe zuerst die Gleichungen für den Block aufgestellt. Aus diesen Gleichungen kriegst du eine Funktion ) . Diese Funktion (Gleichung) brauchst du, weil N_2 auch auf den Keil wirkt.
Danach machst du dasselbe mit dem Keil und kriegst am Schluss eine Funktion ) .
Am Schluss setzst du die Werte aus der Aufgabenstellung ein:
Ich frage mich nur gerade, weshalb diese Aufgabe leichter sein soll. Keine Momentenbedingung vielleicht? Das Gleichungssystem an sich hat aber die Tücke, dass viele Vorzeichenfehler möglich sind, wenn man nicht konzentriert arbeitet.
Zudem verstehe ich den Hinweis grade nicht. Zumindest nicht, in welcher Form er relevant wäre. Zumindest nicht auf eurer Stufe; no offense.
| Beschreibung: |
|
| Dateigröße: |
11.12 KB |
| Angeschaut: |
17166 mal |
|
|
|
|
lena18
Anmeldungsdatum: 11.10.2009
Beiträge: 464
|
| lena18 Verfasst am: 14. Okt 2009 23:05 Titel: |
|
|
Hallo Gajeryis
Ich danke dir für deine Hilfe.
Die erste Aufgabe habe ich gelöst (Danke  )
Zum 2. Beispiel:
Ich habe es so gerechnet wie du es beschrieben hast. Bei mir bleibt N1 in der F Gleichung irgendwie übrig.
F={[N1*(mü+tana)+GB]*cosa} * (sina*(1-mü²)+2cosa*mü)+GK*mü
ich wäre um einen Rat sehr dankbar
ich bring das einfach nicht fertig
Heute haben wir wieder ein neues Beispiel bekommen und ich bring da auch nicht das Richtige Ergebnis raus. Irgendwie klappt das nie bei mir...
Weiss auch nicht was ich falsch mach oder ob ich gar falsch denke.
Ich danke im Voraus
lena
|
|
|
Gajeryis
Anmeldungsdatum: 08.10.2009
Beiträge: 194
Wohnort: CH - Bern
|
| Gajeryis Verfasst am: 15. Okt 2009 14:44 Titel: |
|
|
Dann werde ich mal vorrechnen.
Ich führe folgende Richtungen ein: y vertikal nach oben, x horizontal nach recht, F wirkt horizontal nach links, GB und GK je vertikal nach unten.
Block y:
auflösen nach
 \cdot N_{2} - G_{B} ] \qquad \rm{(1)})
Block x:
auflösen nach
 \cdot N_{2} \qquad \rm{(2)})
(1) = (2) setzen und nach N2 auflösen:
 \cdot \cos{\alpha} } \qquad \rm{(3)})
Keil y:
auflösen nach
 \cdot N_{2} + G_{K} \qquad \rm{(4)})
Keil x:
auflösen nach
 \cdot N_{2} \qquad \rm{(5)})
(4) in (5):
 \cdot \sin{\alpha} ] \cdot N_{2} \qquad \rm{(6)})
(3) in (6), formelle Lösung:
 } + \tan{\alpha} \right) \cdot G_{B})
numerische Lösung:
|
|
|
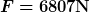
lena18
Anmeldungsdatum: 11.10.2009
Beiträge: 464
|
| lena18 Verfasst am: 15. Okt 2009 22:14 Titel: |
|
|
Hallo
Danke für deine Antwort.
Ich werde es morgen nochmals versuchen zu rechnen.
Laut Ergebnis weicht deine Lösung von der tatsächlichen ein wenig ab.
7030N sollten sich ergeben, ich selber komme ja nicht mal auf deine Lösung.
Frage: wie kommst du eigentlich auf folgende Formel (90-2alfa)??, wäre nett, wenn du mir das noch erklären könntest.
danke nochmals
lena
|
|
|
Gajeryis
Anmeldungsdatum: 08.10.2009
Beiträge: 194
Wohnort: CH - Bern
|
| Gajeryis Verfasst am: 16. Okt 2009 00:24 Titel: |
|
|
| lena18 hat Folgendes geschrieben: | Laut Ergebnis weicht deine Lösung von der tatsächlichen ein wenig ab.
7030N sollten sich ergeben, ich selber komme ja nicht mal auf deine Lösung. |
Ich hoffe eigentlich schon, nicht selber noch Fehler gemacht zu haben. Ich rufe sonst jeden, der Lust hat, dazu auf, meine Rechnung auf Fehler zu überprüfen. Will dir ja nicht irgend einen Quark andrehen. Aber das Resultat sieht meiner Meinung nach nachvollziehbar aus... hm.
| Zitat: | | Frage: wie kommst du eigentlich auf folgende Formel (90-2alfa)??, wäre nett, wenn du mir das noch erklären könntest. |
Oh. *grins* Ich habe zuerst die formelle Lösung in Excel eingegeben und mir den Graph angeschaut. Ich weiss, das ist geschummelt.
Aber den Beweis kann ich dir nachträglich gerne geben:
|
|
|
lena18
Anmeldungsdatum: 11.10.2009
Beiträge: 464
|
| lena18 Verfasst am: 20. Okt 2009 22:11 Titel: |
|
|
| Gajeryis hat Folgendes geschrieben: |
auflösen nach
[/latex] |
Hallo Gajeryis
Danke für deine Antwort, habe die Aufgabe nochmals gerechnet und festgestellt, dass dein Rechenvorgang zwar richtig ist, du dich aber im Vorzeichen etwas vertan hast.
Das obige sollte + sein
Vielen vielen Dank nochmals für deine Hilfe
|
|
|
Gajeryis
Anmeldungsdatum: 08.10.2009
Beiträge: 194
Wohnort: CH - Bern
|
| Gajeryis Verfasst am: 21. Okt 2009 01:05 Titel: |
|
|
Du hast Recht, da hatte ich einen Vorzeichenfehler.
| Zitat: | | Ich hoffe eigentlich schon, nicht selber noch Fehler gemacht zu haben. |
Umsonst gehofft. 
Aber eigentlich super: Du hast es soweit kapiert, wie's geht, dass du schon deinen Helfer korrigieren kannst. 
|
|
|
lena18
Anmeldungsdatum: 11.10.2009
Beiträge: 464
|
| lena18 Verfasst am: 21. Okt 2009 20:49 Titel: |
|
|
Hallo
Nein, so ein schlauer Student wie du bin ich noch nicht , denn ich habe schon wieder ein kleines Problem und würde wieder  brauchen
Meiner Meinung nach fehlt doch noch irgend eine Angabe: Gewicht und reibwert vllt?
Ein Wagen soll mit konstanter Geschwindigkeit eine geneigte Bahn herunterfahren. Welcher Neigungswinkel ist erforderlich, wenn die Lagerreibung gegenüber der Rollreibung vernachlässigt werden kann?
f=0,05cm, Durchmesser des Rades d=0,35 
Ich hätte gedacht, dass F(fahrtrichtung)=FR-FH wäre
dann wäre F=FG*sinalfa*f/r
FN=FGy
FR=FN*mü=FGy*mü=
Ich wäre froh wenn mir geholfen werden könnte.
Vielen vielen Dank im Voraus
Grüsse lena
|
|
|
Gajeryis
Anmeldungsdatum: 08.10.2009
Beiträge: 194
Wohnort: CH - Bern
|
| Gajeryis Verfasst am: 21. Okt 2009 23:42 Titel: |
|
|
*grins* Musste grade nachsehen, wie die Rollreibung definiert ist.
Ich beziehe mich auf den wikipedia-Artikel "Rollwiderstand".
Wenn ich mal richtig spekuliere, sind deine gegebenen Werte f [cm] und d [m] die Werte, welche du für den Rollreibungswiderstandsbeiwert benötigst.
Nach wikipedia ist dieser wie folgt definiert:
wobei d deinem f und R deinem d/2 entsprechen würde, d.h. es wird
Die Rollreibung an sich ist F_R = c_roll * N
Die Geschwindigkeit soll konstant sein, also müssen sich die Kräfte längs der Bewegungsrichtung aufheben.
F_R wirkt längs, du brauchst somit N aus alpha und m*g.
Die treibende Kraft errechnest du ebenfalls aus alpha und m*g.
Als Lösung kriegst du eine Lösung alpha = Funktion( f, d ).
Hinweis: Bringe f und d noch in die selbe Einheit, damit du nicht 10er-Potenz-Fehler für den Rollreibungsbeiwert kriegst.
|
|
|
lena18
Anmeldungsdatum: 11.10.2009
Beiträge: 464
|
| lena18 Verfasst am: 23. Okt 2009 21:12 Titel: |
|
|
Hallo
Vielen Dank wieder für deine hilfreiche Antwort.
Ich habe es lösen können, 0,16°, irgendwie klingt das sehr wenig
Wir haben heute wieder eine Aufgabe bekommen und ich dachte ich könnte es wie du machen mit dem getrennten Freimachen der Teile. Irgendwie klappt das bei mir nie, ich bin, so denke ich, zu blöd für dieses Fach.
Könntest du mir erklären, was falsch ist und warum?
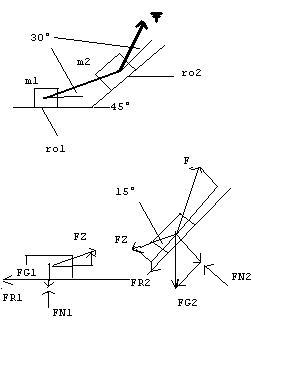
Zwei Massen m1 und m2 sind durch eine gewichtslos angenommene Stange verbunden. Sie sollen durch eine Kraft nach rechts bzw. oben verschoben werden. Wie groß muss F mindestens sein, wenn Alfa 30° beträgt? FG1=200N, FG2=300N, ro1=15, ro2=30°
Also Betrachtung des Klotzes 1
FR1=Fzx=(FG1-Fzy)*tanro1=cos30*Fz
sinalfa*FZ=Fzy
(FG1-sinalfa*Fz)*tanro1=cos30*Fz
Fz=(FG1*tanro1)/(sin30*tanro1+cos30)
Klotz 2
cos15=Fzx/Fz
sin15=Fzy/Fz
cos30=Fx/F
sin30=Fy/F
cos45=FG2y/FG2
sin45=FG2x/FG2
Summe Fy
FN2-FG2y+Fzy+Fy=0
Summe Fx
FG2x+Fzx+FR2-Fx=0
bei x
FN2=FG*cos45-Fz*sin15-F*sin30
bei y
FR2=Fx-Fzx-FG2x
FN2*tanro2=F*cos30-Fz*cos15-FG*sin45
(FG*cos45-Fz*sin15-F*sin30)*tanro2=F*cos30-Fz*cos15-FG*sin45
FG*cos45*tanro2-Fz*sin15*tanro2-F*sin30*tanro2=F*cos30-Fz*cos15-FG*sin45
FG*(cos45*tanro2+sin45)+Fz*(cos15-sin15*tanro2)-F*(sin30*tanro2+cos30)=0
F={FG2*(cos45*tanro2+sin45)+(cos15-sin15)*[(FG1*tanro1)/(sin30*tanro1+cos30)]}/(sin30*tanro2+cos30)
Ich habe ein Ergebnis von 645N anstatt 328N
Vielen vielen DAnk im Voraus
lena
| Beschreibung: |
|
| Dateigröße: |
12.36 KB |
| Angeschaut: |
14851 mal |
|
|
|
|
lena18
Anmeldungsdatum: 11.10.2009
Beiträge: 464
|
|
|
Gajeryis
Anmeldungsdatum: 08.10.2009
Beiträge: 194
Wohnort: CH - Bern
|
| Gajeryis Verfasst am: 24. Okt 2009 12:55 Titel: |
|
|
Moin!
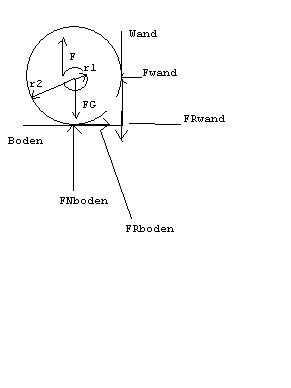
Die Scheibe soll also an Ort in Rotation kommen. Dann hast du aber in deiner Skizze (du hast langsam Übung ) die Wandreibungskraft in die falsche Richtung gezeichnet. Die Scheibe würde im Uhrzeigersinn rotieren, als müssen beide Reibungskräfte dieser Bewegung entgegenstehen. Aber ich denke mal, dies war nicht ein prinzipieller Denkfehler deinerseits.
Zur Aufgabe:
Den Punkt, wo die Scheibe die Wand berührt, nenne ich W, den Punkt unten nenne ich B.
Stelle wieder drei Gleichgewichtsbedingungen auf:
R_horizontal = 0 führt zu F_W = F_RB (keine anderen horizontalen Kräfte vorhanden
R_vertikal = 0 führt zu einer Gleichung mit F, F_B und F_G. Du brauchst nun noch eine Gleichung, um F_B durch F und F_G auszudrücken.
M_W = 0 führt zu dieser gesuchten Gleichung.
Nach F auflösen und du kriegst eine Lösung aus F_G, my und r1/r2.
|
|
|
lena18
Anmeldungsdatum: 11.10.2009
Beiträge: 464
|
| lena18 Verfasst am: 24. Okt 2009 18:39 Titel: |
|
|
Hallo
Ich bin dir echt sehr dankbar, dass du mir dabei immer hilfst, mein Lehrer hat sich schon gewundert, wie ich das mache,
(bin von einem 4er auf einen 3er gerutscht freu... langsam macht dieses Fach richtig Spaß )
Ich weiß trotzdem nicht was ich falsch mache, ich komme nicht auf die Lösung, habe es schon mehrmals gerechnet, kommt immer das Selbe heraus.
Summe Fx
Fw-FRB=0, Fw=FRB=müy*FB
Summe Fy
FG-F-FB-FRw=0 -> FRw=müy*Fw
FG-F-FB-müy*Fw=0
FG-F-FB-müy*müy*FB=0
FB=(FG-F)/(1+müy²)
Summe M
FB*r2-FRB*r2-FG*r2+F*(r2+r1)=0
FB*r2-FRB*r2-FG*r2+F*(3r2/2)=0
FB-FRB-FG+1,5F=0
FB-müy*FB-FG+1,5F=0
FB=(FG-1,5F)/(1-müy)
FB=FB
FG-1,5F/1-müy=FG-F/1+müy²
umgeformt
F=FG*(müy²+müy)/(müy+1,5müy²+0,5)
F=877,32N
Aber F aus Lösung 4905N??
Müsste dann die Reibung nicht 0 sein?
Ich verstehe das einfach nicht.
Vielen Dank
Lena
Hallo ich schreibe es einfach hier mal rein.
Bei der 2. Hausaufgabe habe ich eine Gleichung mit F und FG, müy und alfa als Lösung, aber jetzt habe ich ja F und müy nicht, wie mache ich das jetzt?
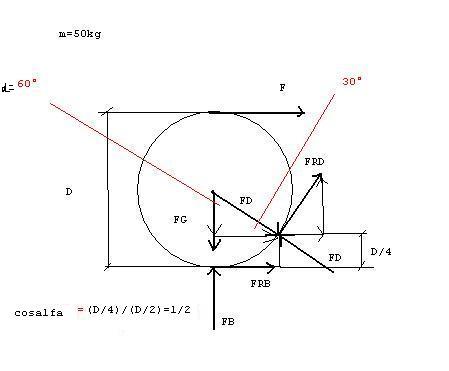
Eine Walze mit der Masse m=50kg soll durch ein am Umfang befestigtes waagrecht verlaufendes Seil die Stufe hinaufgezogen werden.
Wie gross müssen die Seilkraft F und die Haftreibzahl müy0 zwischen Stufenkante und Walzenkante mindestens sein, damit die Walze nicht an der Kante abrutscht.
Unter welchem Winkel muss man mit einer tangetialen Seilkraft ziehen, damit man mit einer möglichst geringen Kraft auskommt? Wie gross muss in diesem Fall müy0 wenigsten sein?
Ich hoffe das Freimachen ist jetzt fehlerlos
Danke vielmals
lg Lena
| Beschreibung: |
|
| Dateigröße: |
14.57 KB |
| Angeschaut: |
15363 mal |
|
|
|
|
Gajeryis
Anmeldungsdatum: 08.10.2009
Beiträge: 194
Wohnort: CH - Bern
|
| Gajeryis Verfasst am: 24. Okt 2009 21:53 Titel: |
|
|
| lena18 hat Folgendes geschrieben: | | Ich bin dir echt sehr dankbar, dass du mir dabei immer hilfst, mein Lehrer hat sich schon gewundert, wie ich das mache, (bin von einem 4er auf einen 3er gerutscht freu... langsam macht dieses Fach richtig Spaß ) |
Freut mich, dies zu lesen. Die Rechnung für die Nachhilfestunden kommt Ende Monat. *frechgrins*
Scherz beiseite: Ich bin immer froh, wenn ich jemandem helfen kann; vor allem jemandem, der die Hilfe auch dankbar annimmt und schätzt.
| lena18 hat Folgendes geschrieben: | | Ich weiß trotzdem nicht was ich falsch mache, ich komme nicht auf die Lösung, habe es schon mehrmals gerechnet, kommt immer das Selbe heraus. |
Ich komme ebenfalls auf die 877.32 N.
Die gegebene Lösung F = F_G macht auch Sinn. Denn sobald F >= F_G ist, wird die Scheibe angehoben und wir haben keine Kontaktkräfte mehr, die Reibwerte müssten nicht gegeben werden. Da nun F nicht am Scheibenschwerpunkt angreift, dreht sie sich. Von dem her ist die Aufgabe mit F = F_G auch erfüllt.
Es ist aber nicht die geringste Kraft F, bei der Bewegung auftritt. Das wäre dann eben unsere Lösung.
Sonst fragst du einfach deinen Lehrer, weshalb dort diese Lösung steht.
Zur nächsten Aufgabe:
Teilaufgabe eins
Zu deiner Skizze: Da sind ein paar Kräfte zu viel vorhanden. Überleg' dir mal, was mit F_B passiert, sobald die Walze auch nur um einen Millimeter angehoben wurde. Sollte dir das Gleichungssystem etwas vereinfachen.
Weiter bin ich mir nicht sicher, wie du F_D eingeführt hast. F_D ist eine Kontaktkraft auf die Walze, steht also senkrecht auf den Kreis.
Ich werde alpha so verwenden, wie du es eingeführt hast: Als Winkel (fast) Berührungspunkt Boden B - Walzenachse M - Berührungspunkt Stufe D.
Ich mache es dir einfach, die Aufstellung der Gleichgewichtsbedingungen ist nun wirklich zu trivial, um sie zu verheimlichen. Deshalb hier gleich der formelle Lösungsweg:
Moment um M: F = my * F_D (1)
Horizontale: F = sin(a) * F_D (2)
Da beide Gleichungen (1) und (2) stimmen müssen, kriegst du so my = sin(a).
Vertikale: F_G = cos(a) * F_D (3)
Mit (2) und (3) kriegst du F = tan(a) * F_G
Teilaufgabe gelöst.
Teilaufgabe zwei:
Nun wird das Seil nicht mehr fix horizontal gezogen.
Ich führe den Winkel beta ein, positive Richtung Gegenuhrzeigersinn, 0° bei F horizontal nach rechts (entspricht Teilaufgabe eins).
Wir suchen die minimale Seilkraft in Abhängigkeit des Winkels beta.
Wir stellen wieder die Gleichgewichtsbedingungen auf.
Das Moment verändert sich formell nicht, F greift immer tangential an.
Die Horizontale verändert sich, da nur noch die horizontale Komponente von F einwirkt.
Die Vertikale verändert sich, da neu die vertikale Komponente von F mitträgt.
Dann löst du nach F auf. Du hast nun eine Funktion in der Form F = F(F_G, alpha, beta).
Wir suchen F(beta) -> minimal.
Aus der Analysis erinnerst du dich vielleicht noch an das Thema "Kurvendiskussion". Die erste Ableitung einer Funktion f(x) nach x (geschrieben f'(x) oder df/dx ) ist die Steigung der Kurve an der Stelle x. Positive Steigung ist ein Ansteigen von f(x) in Richtung positiven x. Die zweite Ableitung ( f''(x) oder (d^2)f/(dx^2) ) ist die Veränderung der Steigung an der Stelle x.
Wenn das Minimum einer Funktion gesucht wird, suchen wir nach einer Stelle, an der die Kurve eine "Senke" hat. Im tiefsten Punkt der Senke ist die Steigung = 0 und die Steigung wird (in Richtung positivem x) grösser, die Veränderung der Steigung ist also positiv.
Für das Minimum der Seilkraft bezüglich beta leitest du die Gleichung F nach beta ab. Die Lösung muss folgende Bedingungen erfüllen:
dF/dbeta = 0 (Steigung = 0, ist also ein Extremalwert)
(d^2)F / (dbeta^2) > 0 (Sei ein Minimum)
Dabei kannst du dich auf Werte für beta zwischen -90° und +90° beschränken, andere Winkel sind unsinnig.
Das ergibt dir F_min, my kannst du analog Teilaufgabe eins bestimmen.
|
|
|
lena18
Anmeldungsdatum: 11.10.2009
Beiträge: 464
|
| lena18 Verfasst am: 25. Okt 2009 22:21 Titel: |
|
|
[quote="Gajeryis"] | lena18 hat Folgendes geschrieben: |
Die Rechnung für die Nachhilfestunden kommt Ende Monat. *frechgrins*
|
Na, da bin ich mal gespannt 
Nein ich bin echt froh, dass du mir hilfst.
Tut mir leid, aber die Teilaufgabe 2 verstehe ich überhaupt nicht. Die Kurvendiskussion war auch nie meine Stärke.
Was ist eine Senke? Ich glaube ohne Zeichnung oder so werde ich das nie verstehen.
Wieso hast du bei der ersten Teilaufgabe den Drehpunkt als Mittelpkt. des Kreises genommen und nicht den Auflagepkt.?
Ausserdem wieso kommen jetzt bei der 2. Teilaufgabe nicht die Komponenten von FRD und FD bei summe x und y dazu? Du hast doch irgendwo mal bei diesem masselosen Stangenbeispiel gesagt, dass doch die Komponenten von den Reibkräften fehlen etc.
Als Lösung im Buch habe ich
a) F=289N müy0=0,577
b.)F'=217N, müy0'=0,866, alfa 60°
Ok mag sein, dass sie A und B vertauscht haben, aber wieso wird die Kraft geringer, tanalfa ist doch größer als 1?
Jetzt ist das gleich so viel auf einmal, was ich nicht verstehe, ich entschuldige mich dafür und wäre dir dankbar für eine möglichst einfache Erklärung.
Lena
|
|
|
Gajeryis
Anmeldungsdatum: 08.10.2009
Beiträge: 194
Wohnort: CH - Bern
|
| Gajeryis Verfasst am: 26. Okt 2009 00:54 Titel: |
|
|
| lena18 hat Folgendes geschrieben: | Die Kurvendiskussion war auch nie meine Stärke.
Was ist eine Senke? Ich glaube ohne Zeichnung oder so werde ich das nie verstehen. |
Eine Senke ist das 'Gegenteil' eines Hügels.
Die Hügelspitze in einer Funktion ist ein Extremalwert, nämlich ein Maximum, einer Funktion.
Die Sohle einer Senke in einer Funktion ist entsprechend ein Minimum.
*Nachtrag: Für eine "Zeichnung" werde ich weiter unten noch einen Link posten.
| Zitat: | | Wieso hast du bei der ersten Teilaufgabe den Drehpunkt als Mittelpkt. des Kreises genommen und nicht den Auflagepkt.? |
Die Momentenbedingung kann man um einen beliebigen Punkt machen. Da ich eine möglichst einfache Gleichung haben wollte, die mir my gibt, habe ich den Walzenmittelpunkt gewählt. Da F_D und F_G durch den Mittelpunkt zeigen, gehen sie nicht ins Moment um die Mitte ein, zudem ist der Hebelarm (Walzenradius) für beide relevanten Kräfte gleich und kommt nicht in die Rechnung. Also ergibt sich eine sehr einfache Beziehung zwischen Seilkraft und Reibungskraft:
})
| Zitat: | | Ausserdem wieso kommen jetzt bei der 2. Teilaufgabe nicht die Komponenten von FRD und FD bei summe x und y dazu? |
Äääähm... *oops*. Ich sehe, ich habe die auch schon bei der ersten Teilaufgabe vergessen, reinzunehmen. Da hast du gut aufgepasst. *Lob*
Zu meiner Verteidigung, ich habe gestern grade mal 3h geschlafen, da konzentriert es sich äusserst schlecht.
Hier noch die allgemeine Formel für Teilaufgabe 2, Teilaufgabe 1 ist dann nur mit  :
Horizontal:  \cdot F_{D} \quad {( 2 )})
Vertikal:  \cdot F_{D} \quad {( 3 )})
Aus (1) und (2) kriegst du
Aus (3) und (1) kriegst du
Für Teilaufgabe 1 kriege ich mit F_G = 50kg * 9.81 N/kg
my ist ebenfalls eine Funktion von beta, also muss für F_S(beta) weiter aufgelöst werden:
*Nachtrag: Mit dem JAVA-Plotter von Arndt Brünner kannst du dir die Funktion ansehen. Eingabe wie folgt: " 1 / (1 + 0.577*cos(x) + sin(x)) ". Bei "1. Ableitung" Häkchen setzen. Staunen.
Um einen Minimalwert zu finden, setzen wir die erste Ableitung = 0.
Für die Ableitung mache ich folgende Substitution:
Ich leite die Funktion f(u) nach u ab:
 = \frac{d}{d u} \left( \frac{1}{u} \right) = u' \cdot \left( \frac{-1}{u^{2}} \right) \stackrel{!}{=}0)
Fürs bestimmen der Lösung reicht es, u' = 0 nachzuweisen. u' ist:
Vereinfacht sich zu: 
Den Nachweis, dass die zweite Ableitung positiv ist, lasse ich hier mal weg, da das gefundene beta ein plausibles Resultat darstellt; es liegt zwischen 0 und 90 Grad.
Dies ergibt als Resultat:
| Zitat: | Als Lösung im Buch habe ich
a) F=289N müy0=0,577
b.)F'=217N, müy0'=0,866, alfa 60° |
Diese Lösungen wurden mit g = 10.0 gerechnet und gerundet.
Ich hoffe, dass ich mit dieser nachträglichen Korrektur deine Verwirrung wieder gelöst habe. Möchte mich für die Rechenfehler nochmals entschuldigen.
|
|
|
lena18
Anmeldungsdatum: 11.10.2009
Beiträge: 464
|
| lena18 Verfasst am: 27. Okt 2009 20:55 Titel: |
|
|
Hallo
Danke vielmals für deine Antwort.
Irgendwie ist mir das alles viel zu hoch.
Auf folgende Formeln komme ich ja noch ohne deiner Aufstellung aller Gleichgewichtsbedingungen: (entschuldigung, aber ich bin trotzdem noch Fachneuling im Gegensatz zu dir deshalb bitte bei komplizierten Formeln mit Herleitung)
Hier noch die allgemeine Formel für Teilaufgabe 2, Teilaufgabe 1 ist dann nur mit :
Horizontal:
Vertikal:
Aus (1) und (2) kriegst du
Aus (3) und (1) kriegst du
aber du hast doch gesagt, dass für die Teilaufgabe 1 nur der Winkel ß gleich 0 wäre. Also hätte ich dann für
müy=tanalfa=sinalfa/cosalfa=(Wurzel3/2)/(1/2)=(Wurzel3/2)*2=Wurzel3??? anstatt 1/Wurzel3
my ist ebenfalls eine Funktion von beta, weiss nicht mehr was das zu bedeuten hat, wie oder woher weiß man das?
##
Wo das müy ist und woher das cot kommt, leuchtet mir nach langer Überlegung auch nicht ein. Tut mir echt leid, dass ich mir hier leider sehr schwer tue. Könntest du es mir bitte erklären?
Ich denke folgendes lasse ich mal ausser Acht, bis ich weiß wie die vorherigen Formeln hergeleitet wurden.
Danke vielmals im Voraus
Lena[/b]
|
|
|
Gajeryis
Anmeldungsdatum: 08.10.2009
Beiträge: 194
Wohnort: CH - Bern
|
| Gajeryis Verfasst am: 27. Okt 2009 22:42 Titel: |
|
|
| lena18 hat Folgendes geschrieben: | | (entschuldigung, aber ich bin trotzdem noch Fachneuling im Gegensatz zu dir deshalb bitte bei komplizierten Formeln mit Herleitung) |
Entschuldige, ich habe gehofft, die Erklärungen zum Vorgehen im Originalpost würden sich gut mit den neuen Formeln ergänzen.
| Gajeryis hat Folgendes geschrieben: | Aus (1) und (2) kriegst du
Aus (3) und (1) kriegst du
 |
| lena18 hat Folgendes geschrieben: | aber du hast doch gesagt, dass für die Teilaufgabe 1 nur der Winkel ß gleich 0 wäre. Also hätte ich dann für
müy=tanalfa |
Vorsicht, du hast da einen Fehler:
cos(0) ist 1, nicht null. Dadurch ergibt sich: 
| Zitat: | | "my ist ebenfalls eine Funktion von beta", weiss nicht mehr was das zu bedeuten hat, wie oder woher weiß man das? |
| Zitat: | | Wo das müy ist und woher das cot kommt, leuchtet mir nach langer Überlegung auch nicht ein. Tut mir echt leid, dass ich mir hier leider sehr schwer tue. Könntest du es mir bitte erklären? |
"ist eine Funktion von beta" ist ein anderer Satz für "hängt von beta ab". In der Formel für my ist das beta drin, nämlich im cosinus(beta).
Wenn du nun die Gleichung für F_S nach beta ableiten willst, musst du erstmal alle versteckten betas sichtbar machen, sonst kommst du auf ein falsches Ergebnis.
Beispiel: Du hast  = \kappa \cdot t^{2} \quad)
Die Ableitung nach t, wenn kappa eine Konstante ist, ist:
 = \kappa \cdot 2t)
Wenn nun aber kappa ebenfalls eine Funktion von t ist, z.B.  = \sin{t}) , verändert sich die Ableitung zu:
 = \cos{t}\cdot t^{2} + \sin{t} \cdot 2t)
Siehst du den Unterschied zur ersten Berechnung?:
 = \sin{t} \cdot 2t)
Deshalb sollte man keine versteckten Sachen haben, wenn man z.B. eine Funktion ableiten oder integrieren will.
Zurück zur Aufgabe:
Du hast im Nenner das 1/my drin. 1/my ist aber keine Konstante, sondern von beta abhängig:
Nun setzen wir dies in die Gleichung für F_S ein:
Ich forme ein wenig um:
Im ersten Summanden wird  . Und es kommt noch ein kleiner Trick: Die beiden mittleren Summanden im Nenner kann man mit einer geschickten Ausklammerung vereinfachen:
 + \sin{\beta}})
Hier ist mir ein Fehler passiert, ich hatte das 1/sin(a) vergessen und nur das 1 hingeschrieben. Auf die Lösung hatte dieser Fehler aber keinen Einfluss. Trotzdem Entschuldigung für die entstandene Verwirrung. Manchmal sieht man vor lauter latex die Rechnung nicht mehr.
Deshalb nun richtig:
Jetzt können wir nach beta ableiten, da nirgends mehr ein beta versteckt ist.
Ich substituiere den gesamten Nenner durch u:
 = \frac{d}{d\beta}\frac{1}{u})
Die Substitution klappt nun mit der Kettenregel (bei Unklarheiten diesbezüglich siehe den Thread von Steve08)
)
Da wir ein Minimum suchen und die Steigung (=1.Ableitung) in einem Minimumspunkt (Sohlpunkt einer Senke) gerade null ist, muss
 \stackrel{!}{=} 0) sein.
Entweder müsste der Nenner unendlich werden, was wir für jedes beta ausschliessen können. Also muss du/dbeta muss null werden. Und das schauen wir uns jetzt an:
 \stackrel{!}{=} 0)
Jetzt können wir die Summanden einzeln ableiten.
Der erste Summand, das 1/sin(a) hängt nicht von beta ab und fällt raus (Ableitung einer Konstante ist null). Deshalb hat sich mein Fehler oben auch nicht auf die Lösung der zweiten Teilaufgabe ausgewirkt.
Der zweite Summand ist von beta abhängig, das cos(beta) muss abgeleitet werden. Das damit multiplizierte cot(alpha) ist nicht von beta abhängig und ist als Konstante zu betrachten.
Der letzte Summand ist ebenfalls von beta abhängig, sin(beta) wird abgeleitet.
Damit ergibt sich
 = ( 0 + \cot{\alpha}*[-\sin{\beta}] + [\cos{\beta}] ) = 0)
Wenn du noch immer Unklarheiten hast, nur her mit den Fragen. Ich bin dafür da, dir die Sache zu erklären.
Mir ist klar, dass diese Aufgabe schwieriger war als die vorherigen. War sie auch für mich, wie du leider mitkriegen musstest. Bisher musstest du "nur" Gleichungssysteme aufstellen und nach einer gesuchten Kraft auflösen. Mit einer Optimierungsaufgabe wie dieser kam ein Baustein mehr dazu: das Ableiten einer Funktion, welche du aus den Gleichgewichtsbedingungen überhaupt erst gekriegt hast. Mir befinden uns jetzt ein Level höher, dass es schwieriger wurde soll dir keine Angst machen, wir schaffen auch diesen Wald gemeinsam zu lichten.
|
|
|
lena18
Anmeldungsdatum: 11.10.2009
Beiträge: 464
|
| lena18 Verfasst am: 28. Okt 2009 20:32 Titel: |
|
|
Hallo Gajeryis
| Zitat: | | Zu meiner Verteidigung, ich habe gestern grade mal 3h geschlafen, da konzentriert es sich äusserst schlecht. |
Jaaa ja, das sagen sie alle, wenn sie nicht rechnen können und es jemandem trotzdem zeigen wollen.
nein Spaß bei Seite.
| Zitat: | Trotzdem Entschuldigung für die entstandene Verwirrung. Manchmal sieht man vor lauter latex die Rechnung nicht mehr.
|
Macht doch nichts, ich sehe es gerade selbst, was das für ein Zeugs ist.
Da hast du dir aber viel Mühe gegeben und dazu noch sehr gut erklärt. Danke vielmals. Ist echt Wahnsinn, was ihr da für jeden tut.
Das mit dem Differenzieren müsste ich mir allerdings nochmals anschauen bzgl. Kettenregel usw.
Frage:
1.)Was ist, wenn zB ein Maximum der Kraft F verlangt wird, dort ist ja die Steigung auch null, nur eben ein Maximum. Was müsste man dann tun?
2.)Wie hätte das mit der 2. Ableitung funktioniert (positive Veränderung?)
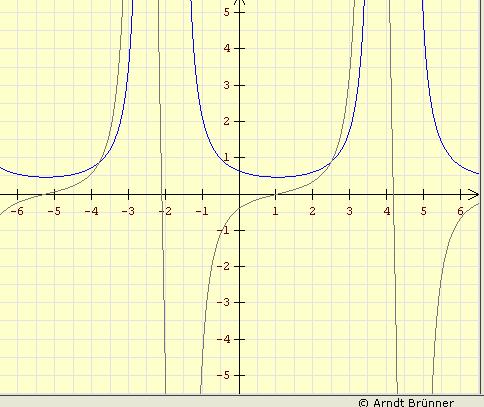
3.)Ich habe mal den Graphen angeschaut, der mir aber absolut nichts sagt, könntest du mir das Wichtigste erklären?
Danke vielmals und gute Nacht
PS: (Könntest Lehrer werden.. )
Lena
| Beschreibung: |
|
| Dateigröße: |
33.15 KB |
| Angeschaut: |
14915 mal |
|
|
|
|
Gajeryis
Anmeldungsdatum: 08.10.2009
Beiträge: 194
Wohnort: CH - Bern
|
| Gajeryis Verfasst am: 29. Okt 2009 12:05 Titel: |
|
|
| Zitat: | | 1.)Was ist, wenn zB ein Maximum der Kraft F verlangt wird, dort ist ja die Steigung auch null, nur eben ein Maximum. Was müsste man dann tun? |
Richtig bemerkt. Wenn man sich das Bild der Funktion vors Innere Auge führt und sich sicher ist, dass innerhalb des plausiblen Wertebereiches (in dieser Aufgabe: innerhalb 0 und 90 Grad) nur eine Extremalstelle ist (z.B. das gesuchte Maximum), dann reicht es, die erste Ableitung null zu setzen.
Wenn aber diese erste Ableitung mehrere Nullstellen innerhalb des gesuchten Wertebereiches hat, dann leitest du die Funktion noch ein zweites Mal nach derselben Variable ab. Dazu kurzer Exkurs:
| Zitat: | | 2.)Wie hätte das mit der 2. Ableitung funktioniert (positive Veränderung?) |
In der Kurvendiskussion schaut man sich mittels mathematischer Mittel an, wie eine Funktion überhaupt verläuft.
Ich gebe eine kleine Analogie: Stell dir vor, eine beliebige Funktion ist das Höhenprofil eines Wanderweges. Die x-Koordinate ist die Horizontaldistanz (Das, was du auf einer Karte rausmessen kannst), die y = f(x) - Koordinate ist die Höhe über Meer jedes Wegpunktes.
Wenn du nun entlang des Weges (=in positiver x-Richtung) spazierst, kannst du dir anschauen, wie der Weg in vertikaler Richtung verläuft: Du kannst zwischen zwei Punkten den horizontalen Abstand (delta x) messen und den Höhenunterschied (delta y) ermitteln. Höhenunterschied durch Abstand ergibt dir das Mass für die Steigung. Das Dumme dabei ist, dass du so die Steigung über diese Strecke nur im Mittel kennst. Allfällige Bodenwellen dazwischen werden nicht berücksichtigt. Deshalb wird das delta x ganz klein gemacht, um keine Bodenwelle zu verpassen. Um dies auch mit Buchstaben auszudrücken, wird die Strecke nun dx, der Höhenunterschied dy bezeichnet; die Steigung ist dann dy/dx. Mathematiker haben herausgefunden, dass die Ableitung einer Funktion (der Höhenlinie) genau die Funktion der Steigung (dieser Höhenlinie) an jedem Punkt des Weges ergibt.
Ok, Zusammenfassung:
Du leitest die Funktion der Höhenlinie ab und kriegst die Steigung: die Veränderung der Höhe entlang des Weges. Gewinnst du an Höhe, hast du eine positive Steigung, verlierst du an Höhe, hast du ein Gefälle, eine negative Steigung.
Nun, wenn eine Ableitung einem also die Veränderung einer Funktion gibt, können wir doch auch die Veränderung der Steigung hinkriegen! May I present: die zweite Ableitung. Wenn wir die Steigungsfunktion ableiten, kriegen wir die Funktion der Veränderung der Steigung entlang des Weges.
Gehen wir einen Hügel hinauf und erreichen wir die Spitze, haben wir zuerst eine positive Steigung, auf der Spitze ist der Weg horizontal, wir haben eine Steigung null, beim hinabgehen wird die Steigung negativ. Die Steigung hat sich also verringert, die Änderung der Steigung ist negativ.
Gehen wir durch eine Senke,haben wir zuerst negative Steigung, danach positive Steigung. Dies ergibt eine positive Veränderung der Steigung.
Gehen wir auf einer geraden Rampe, haben wir zwar eine Steigung, aber eine gleichbleibende. Die Veränderung der Steigung in einem (vertikal) geraden Wegstück ist null.
Damit die zweite Ableitung - die Veränderung der Steigung - einen Wert ungleich null ergibt, reicht schon eine kleine Steigungsänderung, es muss also prinzipiell nicht eine Hügelspitze oder Senke geben. Die Steigung kann sich z.B. auch von +10% auf +5% ändern. Dies nur als Nebenbemerkung.
Exkurs beendet. Zurück zur Frage:
Wenn du mit der 1. Ableitung mehrere Nullstellen findest, dann musst du prüfen, ob diese das gesuchte Maximum oder z.B. eine davon ein Minimum ist. Du leitest die Funktion ein zweites Mal ab (Ableitung der 1. Ableitung). Dann setzst du die x-Werte der Nullstellen ein und schaust, ob die Werte positiv, negativ oder null werden.
Hast du an einer Stelle mit Steigung null einen positiven Wert für die Veränderung der Steigung, ist die Nullstelle der Sohlpunkt einer Senke: ein Minimum.
Hast du einen negativen Wert für die 2. Ableitung, ist die Nullstelle ein Maximum.
Was es auch gibt, ist, dass erste und zweite Ableitung beide null sind. Das wäre dann ein (kurzes) horizontales Geradenstück. Beispiel: Kubische Parabeln haben dies an ihrem Wendepunkt (bei y = x^3 bei x=0).
| Zitat: | | 3.)Ich habe mal den Graphen angeschaut, der mir aber absolut nichts sagt, könntest du mir das Wichtigste erklären? |
Kann ich. Horizontal hast du die x-Achse. Wichtig hier zu erwähnen: Die Zahlenwerte sind die Winkel, aber im Bogenmass, nicht in Grad. 3.14 = pi = 180° Vertikal hast du die f(x)-Achse. Die blaue Linie ist die Funktion f(x), die graue Linie ist die erste Ableitung d/dx f(x) (auch geschrieben f'(x) ).
Was du hier gut siehst: Die blaue Linie hat eine Senke im Bereich um etwa 1 rad. Um den Minimalpunkt (Minimaler Kraftaufwand) genau zu finden, können wir uns die graue Linie anschauen. Dort wo die graue Linie die x-Achse kreuzt, ist der Wert der 1. Ableitung genau null.
Wenn wir den Wert ablesen, erhalten wir den Winkel von etwa 1.047 rad. Durch pi mal 180 Grad gerechnet erhalten wir 60 Grad. Das heisst, wenn beta 60 Grad beträgt, ist F(beta) minimal, nämlich 0.433 mal F_G.
Was du auch siehst:
Geht der Winkel beta gegen -120° (=-2.09 rad) geht die nötige Seilkraft gegen unendlich. Kein Wunder, sie zeigt dann in Richtung der Stufenkante, man drückt das die Walze nur stark auf die Stufe, man zieht sie kaum hoch.
Dasselbe wenn beta zu gross wird, die Seilkraft wird unglaublich gross.
| Zitat: | | PS: (Könntest Lehrer werden.. ) |
Ich hoffe, das war ein Kompliment, keine Beschimpfung.
Aber näää, als Lehrer an einer obligatorischen Schule müsste ich vielen jungen Leuten Zeugs eintrichtern, das sie gar nicht wissen wollen. Als Nachhilfelehrer kann ich jungen Leuten helfen, welche Hilfe wollen.
|
|
|
lena18
Anmeldungsdatum: 11.10.2009
Beiträge: 464
|
| lena18 Verfasst am: 30. Okt 2009 20:00 Titel: |
|
|
Hallo
| Zitat: | | Als Nachhilfelehrer kann ich jungen Leuten helfen, welche Hilfe wollen. |
Ja, Hilfe wollen, es aber nur schwer verstehen.. (so wie ich)
Danke vielmals für die ausführliche Erklärung.
Ich denke, ich habs verstanden.
Es gehört vielleicht nicht hier her, aber wir sollten uns in das Thema Schwerpkt. einarbeiten. Wie ich sehen konnte, wurden schon Beispiele gerechnet.
Zum Beispiel wird der Schwerpunkt über das Produkt von Fläche und Schwerpunktabstand einer Fläche berechnet.
Nehmen wir an es sei ein Rechteck. Da ist es einfach, nämlich befindet sich der Schwerpunkt in der Mitte (Diagnale von Eck zu Eck). Auch wenn es ein Würfel ist, ist es noch einfach, bei einer Kugel weiß man es auch noch logischerweise, aber wie wird der Schwerpunkt bei einer Halbkugel berechnet? Da verläuft die eine Seite ja nicht konstant ins Bild hinein wie beim Klotz und endet irgendwo, sondern bei einer Halbkugel verläuft es ja "rund" ins Bild hinein (Vorderansicht). Da kann man doch nicht den Querschnitt nehmen oder?
Weisst du so überhaupt was ich meine??
Wie funktioniert sowas überhaupt?
Vielen Dank im Voraus
Lena
Habe noch vergessen zu sagen, dass mir gerade einfällt, da du gerade von dx und dy gesprochen hast, könnte es sein, dass man da integrieren muss?
Wenn ja, wie würde man da vorgehen?
|
|
|
Gajeryis
Anmeldungsdatum: 08.10.2009
Beiträge: 194
Wohnort: CH - Bern
|
| Gajeryis Verfasst am: 31. Okt 2009 15:20 Titel: |
|
|
| lena18 hat Folgendes geschrieben: | Es gehört vielleicht nicht hier her, aber wir sollten uns in das Thema Schwerpkt. einarbeiten. Wie ich sehen konnte, wurden schon Beispiele gerechnet.
Zum Beispiel wird der Schwerpunkt über das Produkt von Fläche und Schwerpunktabstand einer Fläche berechnet.
[...] aber wie wird der Schwerpunkt bei einer Halbkugel berechnet? [...]Habe noch vergessen zu sagen, dass mir gerade einfällt, da du gerade von dx und dy gesprochen hast, könnte es sein, dass man da integrieren muss? |
Deine Intuition bewährt sich. Den Schwerpunkt einer beliebigen Fläche, rechnet man tatsächlich per Integralrechnung aus. Dabei teilt man eine Fläche in einzelne Teilchen auf und macht dann eigentlich ein gewichtetes Mittel über alle Teilchen.
Exkurs
Ein kleines Beispiel für solch ein gewichtetes Mittel ist der Schwerpunkt des Systems Erde - Mond. Die Erde hat etwa die 81fache Masse der Erde. Wenn wir nun den Abstand des Schwerpunktes von einem beliebigen Bezugspunkt auf der Achse Erde-Mond aus berechnen wollen, rechnen wir:
Abstand zum System-Schwerpunkt = (Abstand zur Erde * Masse der Erde + Abstand zum Mond * Masse des Mondes) / (Gesamtmasse des Systems )
Die Abstände können dabei auch negative Werte haben, wenn der Bezugspunkt zwischen den beiden Körpern liegt.
Du kannst dir diese Rechnung auch wie folgt vorstellen: Du hast eine (masselose) Wippe. Links des Gelenks hast du je die beiden Massen der Erde und des Mondes mit ihren entsprechenden Abständen. Rechts des Gelenks hast du ein verschiebliches Gewicht mit der Masse von Erde und Mond zusammen. Sobald bei Verschieben der Gesamtmasse die Wippe in Ruhe bleibt, hast du den Abstand zum Schwerpunkt gefunden. Wenn du das Momentengleichgewicht um das Gelenk aufstellst, kommst du auf die oben ausgeschriebene Gleichung.
Exkurs beendet.
Für Flächen haben wir keine diskreten Objekte mit einer Masse. Aber wir können die Fläche z.B. senkrecht zur x-Achse in dünne Streifen der Breite dx schneiden. Die Teilflächen können wir jetzt einzeln mit dem Abstand zum Koordinaten-Nullpunkt gewichten und aufsummieren. Als Integral aufgeschrieben:
Das Integral über dA entspricht einem simplen Aufsummieren der Teilflächen, A ist also der Betrag der Gesamtfläche.
Die Teilfläche dA ist die Fläche des Streifens mit Breite dx und Länge y = f(x). Ins Integral eingesetzt:
 \, dx}{\int f(x) \, dx} = \frac{\int x \cdot f(x) \, dx}{A})
Zur Halbkugel:
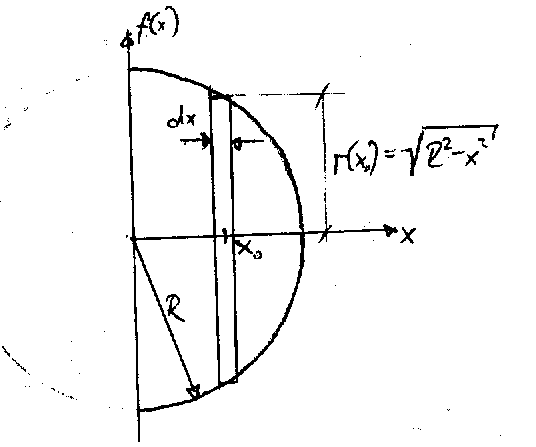
Die Halbkugel sei in einem Koordinatensystem so gerichtet, dass das Zentrum der Vollkugel im Koordinatennullpunkt liegt und die Halbkugel im positiven x-Bereich (x-Achse = horizontale Achse) liegt.
In y-Richtung wirst du mit mir einverstanden sein, wenn der Schwerpunkt auf der x-Achse liegen muss, da die Halbkugel nach oben und nach unten symmetrisch ist.
In x-Richtung geht das nicht so einfach, da benötige ich das Integral.
Die Funktion für eine Kugel ist
 = \pm \sqrt{ R^{2} - x^{2} })
Da diese Funktion um die x-Achse symmetrisch ist, reicht es, den oberen Teil zu betrachten.
Die x-Koordinate des Schwerpunktes ist
Der Teil unter dem Bruchstrich ist die Gesamtfläche des Viertelkreises, also  .
Das Integral über dem Bruchstrich ist für dich möglicherweise nicht gerade das schönste zum Auflösen.
Bei Integralen, welche aus zwei miteinander multiplizierten Teilen bestehen, muss häufig partiell integriert werden. Damit ich eine Ahnung kriege, wie ich zu einem nützlichen Ergebnis komme, schaue ich mir die Sache rückwärts an: Ich suche mir eine Funktion, deren Ableitung dem Inhalt der Integrationsklammer nahe kommt. Hier zum Beispiel:
 ^{\frac{3}{2}} = \frac{du}{dx}\cdot \frac{d}{du} u^{\frac{3}{2}} = \frac{du}{dx}\cdot \frac{3}{2} \cdot u^{\frac{1}{2}} = -2x \cdot \frac{3}{2} \cdot ( R^{2} - x^{2} ) ^{\frac{1}{2}} = - \frac{1}{3}\cdot x \cdot \sqrt{R^{2} - x^{2}})
Bingo. Die Ableitung meines Ansatzes unterscheidet sich nur um die Konstante -1/3 von der zu integrierenden Funktion. Das heisst:
 ^\frac{3}{2} ] )
Da Integralgrenzen gesetzt wurden, rechnen wir also das Ergebnis für das bestimmte Integral:
 ^\frac{3}{2} ]_{0}^{R} = [ -\frac{1}{3} \cdot ( R^{2} - R^{2} ) ^\frac{3}{2} ] - [ -\frac{1}{3} \cdot ( R^{2} - 0^{2} ) ^\frac{3}{2} ] = \frac{1}{3} R^{3})
Der Schwerpunkt ist nun:
|
|
|
lena18
Anmeldungsdatum: 11.10.2009
Beiträge: 464
|
| lena18 Verfasst am: 31. Okt 2009 18:45 Titel: |
|
|
Hallo
Danke für deine Erklärung.
Ich habs mir durchgelesen, aber das ist mir schon viel zu hoch. Im Buch steht irgendwas mit xs=3r/8 anstatt 4r/3pi.
Obwohl ich es mehrfach durchgelesen habe, verstehe ich so gut wie nichts davon. Zum Beispiel wie das mit der Scheibe Fläche und Breite dx und fx gemeint ist und warum fx.dx?
Trotzdem vielen Dank für dein Erklärung. Ich denke ich widme meine Zeit Sachen die verständlicher für mich sind
Lena
|
|
|
Gajeryis
Anmeldungsdatum: 08.10.2009
Beiträge: 194
Wohnort: CH - Bern
|
|
|
Gajeryis
Anmeldungsdatum: 08.10.2009
Beiträge: 194
Wohnort: CH - Bern
|
| Gajeryis Verfasst am: 31. Okt 2009 22:37 Titel: |
|
|
Möchte trotzdem noch kurz auf deine Kommentare zurückkommen.
| lena18 hat Folgendes geschrieben: | | Ich habs mir durchgelesen, aber das ist mir schon viel zu hoch. [...] Obwohl ich es mehrfach durchgelesen habe, verstehe ich so gut wie nichts davon. |
Nun, du hast ja schon vorher, wo es um Extremalwerte ging, Probleme mit Ableitungen etc. gehabt. Da hier Wissen um Integration nötig ist, erstaunt es mich wenig, dass du wieder vor einem Haufen Fragezeichen stehst.
Ableitungen und Integration an sich kann ich dich nicht lehren. Wenn du konkrete Fragen hast, dann kann ich helfen. Konkrete Fragen z.B. wie steve, der etwas zur Kettenregel gefragt hatte, oder wenn du Probleme mit der Lösung eines bestimmten Integrals hast, etc. Für Grundwissen ist eigentlich der Mathelehrer zuständig, das kann dir auch das physikerboard nicht wirklich ersetzen... Du kannst dir natürlich persönliche Nachhilfe in deinem Wohngebiet suchen, wenn du eine Person findest, die dir etwas gut erklären kann, ist das bestimmt kein rausgeworfenes Geld.
| Zitat: | | Zum Beispiel wie das mit der Scheibe Fläche und Breite dx und fx gemeint ist und warum fx.dx? |
Aufsummieren von Teilflächen:
Analog dazu, wie du den Schwerpunkt mehrerer Massen auf einer Wippe finden kannst, indem du die Massen mit dem jeweiligen Abstand zum Gelenk multiplizierst und die Summe durch das Gesamtgewicht teilst kannst du bei Flächen die einzelnen Teilflächen mit dem jeweiligen Abstand zum Koordinatennullpunkt multiplizieren, aufsummieren und das ganze durch die Gesamtfläche teilen; bei räumlichen Körpern wiederum sind es Teilvolumen, welche du mit dem Abstand zum Nullpunkt gewichtest, aufsummierst und durch das Gesamtvolumen teilst.
Nachfrage: Das Beispiel mit Mond und Erde, hast du dies überhaupt verstanden?
Die Breite dx:
Wie du im dem vorigen Posting angehängten Bildchen siehst, ist die gezeichnete Teilfläche nur eine ungenaue Darstellung der tatsächlich zwischen den zwei vertikalen Trennstrichen eingeschlossenen Fläche. Je kleiner aber die Breite der Teilfläche wird, desto näher ist die Fläche des Rechteckes an der tatsächlichen Fläche des Kreis-Schnitzes dran.
Integration ist eigentlich eine Aufsummierung von ganz vielen kleinen Einzelteilen. (Die Integrationsklammer kann man als langgezogenes "S" ansehen und als "Summe:" interpretieren. Genau so wie das Summenzeichen, das griechische Sigma, ebenfalls ein S ist und für Summe steht.) Der Mecano der Integration erlaubt uns, prinzipiell von jeder beliebigen Fläche den Flächeninhalt oder den Flächenschwerpunkt zu berechnen.
|
|
|
lena18
Anmeldungsdatum: 11.10.2009
Beiträge: 464
|
| lena18 Verfasst am: 01. Nov 2009 16:28 Titel: |
|
|
Hallo
Ok, jetzt habe ich es denke ich verstanden mit deiner Skizze.
Ich habe mir schon gedacht, ich versteh das nie.
Also kurz erklärt.
Wenn ich jetzt von links nach rechts in die Halbkugel schaue, dann habe ich lauter Kreise, die immer kleiner werden. (Grösster Kreis r=R, wenn ich das richtig verstehe).
Jetzt geht es darum, dass du also nur eine einzige dünne Scheibe aus diesem Volumen raus schneidest und dessen Breite dann dx nennst. Da der Radius dieser Scheibe nicht mehr R sein kann, sondern <R, nennt man diesen Radius nun r und dieser berechnet sich also über den Pythagoräischen Lehrsatz. y²=r²-x². Der Durchmesser wäre dann in diesem Fall 2y oder der Radius r=y.
Wenn man nun den Schwerpunktabstand möchte, dann nimmt man den Abstand des Volumenteils vom Koordinatenursprung, laut deiner Formel wäre das dann x mal dem Teilvolumen (dieser Scheibe/Fläche *dx). Dieses Integral wird dann also duch das Integral des GEsamtvolumens dividiert.
Ich hoffe, dass ich damit richtig liege, denn jetzt sitz ich schon etwas länger vor deiner Skizze Nicht, dass die Analyse völlig umsonst war
Vielen Dank im Voraus
Lena
hallo ich geb das mal hier rein. wahrscheinlich ist es wieder so eine leichte Aufgabe, aber ich weiss nicht wie ich da rechnen soll.
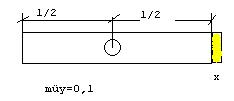
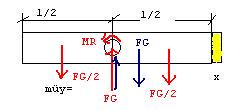
Ein homogener Balken ist auf einen Zapfen mit d=3cm gesteckt. Welche Überlänge x darf ein Teil des balkens haben, wenn der Balken horizontal bleiben soll?
habe mir gedacht, dass
Summe y
FA+FB-FG=0
und summe m
Reibmoment+FA*l/4-FB*(l+2x)/4=0
Reibmoment = FG*müy*r
Andere Überlegung wäre. Das Ganze ist so im Gleichgewicht. Um aus dem Gleichgewicht zu kommen, muss das Reibmoment überwunden werden.
Also muss FG*müy*r=FGneu*(l/2+x)/2 sein
aber was ist FGneu?? vor allem ist das l noch in der Gleichung.
beim letzten Beispiel hab ich nicht mal eine Ahnung wie das funktioniert und wo überhaupt müy wirken soll!
Könntest du mich aufklären?
Entschuldige, dass es jetzt soviel auf einmal ist, aber in 2 Wochen haben wir eine Schularbeit (Reibung aller Arten) und ich hab langsam ein schlechtes Gewissen, weil ich keine Aufgabe selbständig berechnen kann.
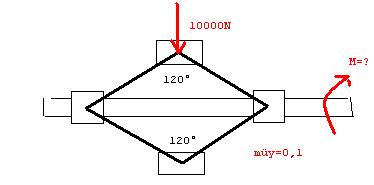
Was die Aufgabe angeht, betrifft es dieses Mal einen Wagenheber.
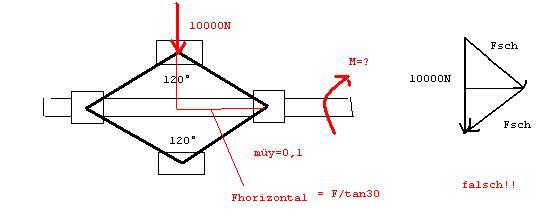
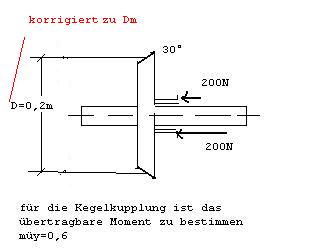
Für den Wagenheber dessen linker Teil der Spindel Rechtsgewinde und dessen rechter Teil Linksgewinde hat, soll das zum Heben und Senken einer Last F=10000N nötige Moment für die gezeichnete Schenkelstellung berechnet werden. Es handelt sich um ein eiingängiges Trapezgewinde Tr 20x4 mit der Gewindetiefe t=2mm
Ich habe gerechnet:
sin60/F=sin60/Fschenkel
Fschenkel = F
cos30=F(Längs)/Fschenkel
F(längs)=8660,25N
Ist nun Fu=FG*tan(alfa+-roh) allgemeingültig?
tanroh=müy
roh=5,71°
tanalfa=4/d2*pi=4/(18*pi)
alfa=4,05°
Fu=FG*tan(alfa+roh)=1489,66N (Heben)
Fu=-250,98N (Senken)??
M=Fu*d2/2=13,41Nm (Heben)?
M=2,26Nm (Senken)?
Muss ich denn nicht über beta/2 oder sowas rechnen beim Trapezgewinde?
Lösungen wären:
balken x=3mm
kegelrad M=48Nm
Wagenheber heben M=54,7Nm senken M=10,1Nm
Ich wäre froh, wenn du mir dabei helfen könntest.
vielen vielen Dank im Voraus
Lena
| Beschreibung: |
|
| Dateigröße: |
9.01 KB |
| Angeschaut: |
23479 mal |
|
| Beschreibung: |
|
| Dateigröße: |
3.88 KB |
| Angeschaut: |
23485 mal |
|
| Beschreibung: |
|
| Dateigröße: |
10.17 KB |
| Angeschaut: |
23486 mal |
|
Zuletzt bearbeitet von lena18 am 01. Nov 2009 19:40, insgesamt 2-mal bearbeitet |
|
|
Gajeryis
Anmeldungsdatum: 08.10.2009
Beiträge: 194
Wohnort: CH - Bern
|
| Gajeryis Verfasst am: 01. Nov 2009 18:21 Titel: |
|
|
Hi lena
Was die Integral-Sache angeht, scheinst du das Prinzip verstanden zu haben.
Zur Aufgabe kann ich dir erst spätabends oder morgen was schreiben, hab grade nur wenig Zeit.
Bis denne.
|
|
|
Gajeryis
Anmeldungsdatum: 08.10.2009
Beiträge: 194
Wohnort: CH - Bern
|
| Gajeryis Verfasst am: 02. Nov 2009 20:50 Titel: |
|
|
Balkenaufgabe:
Du bist nahe dran. Beim Aufstellen der Gleichung
| Zitat: | Also muss FG*müy*r=FGneu*(l/2+x)/2 sein
aber was ist FGneu?? vor allem ist das l noch in der Gleichung. |
hast du nur die eine Hälfte des Balkens drin. Zudem ist der Index "neu" unnötig, da du mit F_G einfach das Gesamtgewicht des Balkens (inkl. Überlänge) formell angibst. Die Reibkraft ist ja ebenfalls vom Gesamtgewicht abhängig, nicht nur vom symmetrischen Teil.
Du kannst es dir auch so überlegen:
Wie weit verschiebt sich der Schwerpunkt des Balkens vom Zapfenmittelpunkt bei Überlänge x?
Dann hast du die Kontaktkraft F_G senkrecht von unten nach oben durch den Zapfenmittelpunkt, die Gewichtskraft F_G um den entsprechenden Betrag seitlich verschoben senkrecht von oben nach unten wirkend und die Reibkraft my*F_G horizontal der Drehrichtung entgegengerichtet, um d/2 nach oben versetzt.
Machst du ein Momentengleichgewicht um den Zapfenmittelpunkt, F_G sollte dabei herausfallen, du kriegst eine Gleichung x(my, d).
Wagenheber:
Gegebene Daten: my = 0.1; F = 10 kN; d_N = 20 mm; m = 4 mm; t = 2 mm
Gesuchte Daten: M_Heben; M_Senken
d_N ist der Aussendurchmesser des Gewindes. m ist der Abstand zwischen zwei Gewindezahn-Mitten.
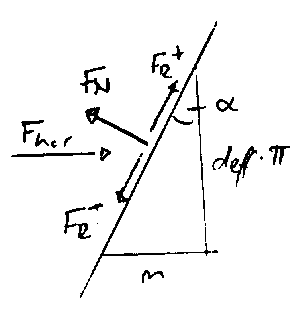
Zuerst brauchen wir die effektiv auf das Gewinde wirkende Kraft F_hor. Wir haben ein Gestänge, welches von oben und unten mit der Kraft F = 10kN belastet wird. Das heisst, die horizontale Kraft kriegen wir mithilfe von Trigonometrie:
Ich definiere mal den Steigungswinkel des Gewindes
wobei
Das d_eff habe ich eingeführt, weil die Reibkraft eher in der Mitte der Gewindestirnfläche wirkt als an der äusseren Kante.
Für die wirkenden Kräfte schaust du dir bitte die Skizze an.
Beim Heben wirken jeweils die tangentialen Komponenten der Reibungskraft und Normalkraft entgegen der Drehung:
Beim Senken wirkt die Reibkraft entgegen, die Normalkraft hilft beim Drehen.
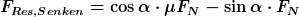
Das entsprechende Moment ist dann die resultierende Kraft mal den Hebelarm:
Habe die Gleichungen noch nicht geprüft und noch keine Resultate gerechnet. Aber ich hoffe, dass ich dir die Idee vermitteln konnte.
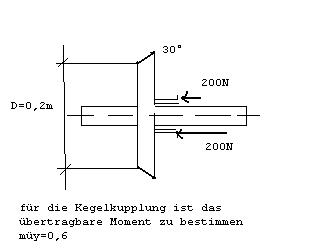
Kegelkupplung:
Eine schöne Skizze, aber kannst du mir einen kurzen Text dazu schreiben? Ich sehe grade nicht, was an was reiben soll.
| Zitat: | | Entschuldige, dass es jetzt soviel auf einmal ist, aber in 2 Wochen haben wir eine Schularbeit (Reibung aller Arten) und ich hab langsam ein schlechtes Gewissen, weil ich keine Aufgabe selbständig berechnen kann. |
Meistens bist du auf dem richtigen Weg. Dir fehlt wahrscheinlich etwas die Routine. Rechne alle gemachten Übungen nochmals ohne die Lösung offen zu sehen. Das hilft dir, Sicherheit zu gewinnen. Unsicherheit erhöht die Fehlergefahr.
| Beschreibung: |
|
| Dateigröße: |
2.62 KB |
| Angeschaut: |
23464 mal |
|
|
|
|
lena18
Anmeldungsdatum: 11.10.2009
Beiträge: 464
|
| lena18 Verfasst am: 03. Nov 2009 21:16 Titel: |
|
|
Hallo Gajeryis
Erstmal vielen Dank für deine ausführlichen Erklärungen. Du hilfst mir immer sehr.
Balkenaufgabe:
Ich habe da also
FG*((l/2+x)/2)-FG*müy*r-FG*(l/2)/2=0
FG gekürzt x=2müy*r=3mm
deine Variante bekomm ich leider nicht her (siehe Skizze blau geschrieben)
FG*x-FG*müy*r=0 (FG*x =GEsamtschwerkraft mal Abstand)
x=müy*r??
Frage:
Was ich immer noch nicht verstehe ist, dass wenn die Überlänge nicht gefragt ist, dann haben wir ein Gleichgewicht (siehe skizze rot geschrieben) und FG mit FG/2 auf beiden Seiten. Wird nun nach Überlänge gefragt, dann haben wir auf einmal überall FG
Wenn man da alle Kräfte in y hat, würde es doch FG+FG-FG=0 sein, ist doch irrsinnig oder? sorry, aber es leuchtet mir einfach nicht ein.
Beim Wagenheber versteh ich nur nicht was ich nun falsch gemacht habe mit meinem Kraftdreieck. Was für eine horizontale Kraft Flängs habe ich überhaupt gerechnet. Wo würde diese denn wirken?
F/sin60=Fsch/sin60
F=Fsch
cos30=Flängs/Fsch
deine Variante (die richtige) wäre ja die links im Wagenheber eingezeichnet.
ausserdem, warum muss ich schlussendlich Das Moment *2 rechnen, damit ich auf 54 und 10Nm komme? diese 10000N wirken ja nur von oben, unten ist ja nur eine Kontaktkraft?!
Das Beispiel mit dem Kegelrad ist leider so im buch eingezeichnet und mit einem Text versehen wie in Skizze. Darum frage ich, wie was wirkt, ich kann mir das auch irgendwie nicht vorstellen, wie es in den zahnrädern aussieht(Kraftwirkung). Nur dass wahrscheinlich die Normalkraft auf den Zahn eine in Achsrichtung und eine radiale Kraft verursacht??!
Ich wäre dir dankbar, wenn du mich wieder aufklären könntest.
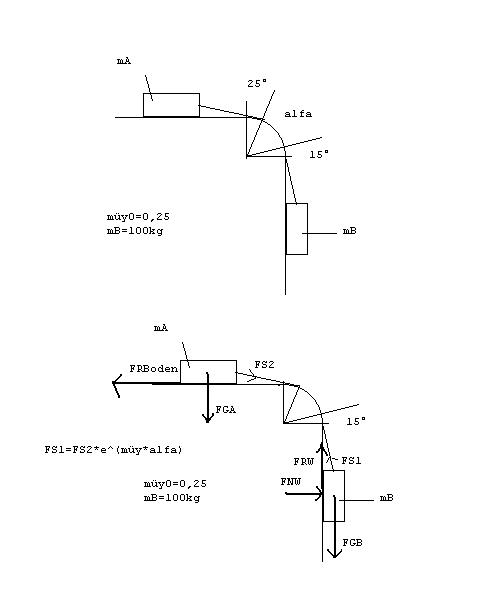
Bei dem neuen Beispiel bräuchte ich wieder einen Tip und zwar, weiss ich nicht wie ich das mit dem Seil zurückrechnen soll. Denn die Reibkraft des mA ist doch auch von mB abhängig, da mA aufgrund des Gewichtes von mB noch mehr reibt oder?
aber wie mache ich das mit der Seilkraft, Fs1 ist ja FS2*e^müy*alfa, ausserdem wirkt die Seilkraft ja schräg nach unten und da ist ja auch kein Winkel angegeben??
skizzen sind im Anhang.
tut mir echt leid, dass ich nun so einige Fragen habe und dich so sehr fordere. entschuldigung.
Vielen Dank im Voraus,
Lena
| Beschreibung: |
|
| Dateigröße: |
5.63 KB |
| Angeschaut: |
23446 mal |
|
| Beschreibung: |
|
| Dateigröße: |
14.29 KB |
| Angeschaut: |
23447 mal |
|
| Beschreibung: |
|
| Dateigröße: |
11.21 KB |
| Angeschaut: |
23447 mal |
|
Zuletzt bearbeitet von lena18 am 03. Nov 2009 21:19, insgesamt einmal bearbeitet |
|
|
lena18
Anmeldungsdatum: 11.10.2009
Beiträge: 464
|
| lena18 Verfasst am: 03. Nov 2009 21:19 Titel: |
|
|
hier wäre noch die letzte skizze
| Beschreibung: |
|
| Dateigröße: |
18.14 KB |
| Angeschaut: |
19978 mal |
|
|
|
|
Gajeryis
Anmeldungsdatum: 08.10.2009
Beiträge: 194
Wohnort: CH - Bern
|
| Gajeryis Verfasst am: 04. Nov 2009 17:26 Titel: |
|
|
Hi lena
Ich habe heute leider kaum Zeit und kann dir deshalb erst morgen ausführlich Antworten, vor allem für die Wagenheber-Aufgabe und die neue Frage werde ich ein paar Skizzen machen müssen. Entschuldige, dass ich dich vertrösten muss.
Nun aber kurz:
| Zitat: | | Was ich immer noch nicht verstehe ist, dass wenn die Überlänge nicht gefragt ist, dann haben wir ein Gleichgewicht (siehe skizze rot geschrieben) und FG mit FG/2 auf beiden Seiten. Wird nun nach Überlänge gefragt, dann haben wir auf einmal überall FG |
So wie du es auf der Skizze eingezeichnet hast, machst du die Rechnung aufwändig. Nicht falsch, aber aufwändig und damit fehleranfällig.
Du hast links den Balkenteil, dessen Gewicht als repräsentative Kraft bei L/4 Abstand nach unten zieht. Den dazu symmetrischen Teil rechts zieht ebenfalls als rep. Kraft im Abstand L/4 nach unten. Das heisst, im Moment um den Zapfenmittelpunkt heben sich die beiden auf. Nun hast du aber den Teil der Überlänge, der ja ebenfalls ein Gewicht hat und nach unten zieht. Wie gross diese Gewichtskraft ist, kriegst du aus dem Verhältnis von x und L heraus. Diese Gewichtskraft hast du in deiner Skizze noch nicht berücksichtigt. Die Kontaktkraft im Zapfen muss dann die Summe aller drei Teile sein, nicht nur des symmetrischen Teiles.
Dieser Weg führt ebenfalls zum richtigen Resultat, es besteht aber eine grössere Gefahr, dass du dich in den Gleichungen verhedderst.
Deshalb habe ich meinen Weg vorgeschlagen:
Der Schwerpunkt eines geraden Balkens mit gleichbleibendem Querschnitt (von der Seite als Rechteck gesehen) ist (in Längsrichtung) immer in der Mitte der Gesamtlänge des Balkens. Eine repräsentative Gewichtskraft greift in diesem Schwerpunkt an.
Wenn du einen Balken der Länge L hast, greift "F_G = g * L * Querschnittsfläche * Dichte = L * Konstante" bei L/2 an. In diesem Fall ist der Zapfen genau bei L/2, also gibt es bei Überlänge=null kein Moment, das aufgenommen werden muss.
Wenn du nun einen Balken der Länge L+x (x ist die Überlänge) hast, greift "F_Gü = (L+x) * Konstante" bei (L+x)/2 an, also x/2 neben dem Zapfen. Die Kontaktkraft im Zapfen ist dann natürlich F_N = F_Gü, damit in vertikaler Richtung Kräftegleichgewicht herrscht. Da nun die Gewichtskraft nicht mehr durch den Zapfenmittelpunkt geht, muss dieses Moment durch die Reibungskraft am Zapfen aufgenommen werden. Die Reibungskraft wiederum ist d/2 vom Zapfenmittelpunkt entfernt.
kraftmalkraftarmistlastmallastarm: F_R * d/2 = F_G * x/2
Ich hoffe, damit hast du genügend "Aufklärung" erhalten, was diese Aufgabe betrifft.
Für mehr habe ich heute leider nicht Zeit, du kriegst morgen Nachmittag von mir den Rest... der Aufgaben.
|
|
|
lena18
Anmeldungsdatum: 11.10.2009
Beiträge: 464
|
| lena18 Verfasst am: 04. Nov 2009 20:57 Titel: |
|
|
Hallo
Also ich weiß nicht, das mit dem Erklären hast du einfach drauf
Alles was ich bisher gerechnet habe, ist auf deine Rechenweise immer logisch gewesen und einfacher ist es auch noch.
Also deine Variante ist ja FG*x/2-FG*müy*r=0
x=2müy*r
Habs also nochmals kompliziert auch noch gerechnet, ob ich es wirklich verstanden habe :
Also
FN=FG/2+FG/2 = FG
(FG/2)*(l/4-x/2) + FG*müy*r - (FG/2)*(l/4+x/2)=0
l/8 - x/4 + müy*r - l/8 - x/4=0
-x/4 + müy*r - x/4=0
x=2müy*r
Vielen vielen Dank noch
Bezüglich des Wagenhebers habe ich noch eine Frage und zwar, wieso ist es im Buch eigentlich so kompliziert erklärt mit Fu=FG*tan(alfa+roh) etc. und bei Trapezgewinde müy'=müy/cos(beta/2) (beta=30°)
Das müy' muss ich ja so verwenden in deiner REchnung, aber Fu?
Deine Variante ist für mich logischer.
Danke
Lena
|
|
|
|
|
Registrieren
Login
FAQ
Suchen
