| Autor |
Nachricht |
fummi
Anmeldungsdatum: 06.07.2008
Beiträge: 1
|
 fummi Verfasst am: 06. Jul 2008 12:36 Titel: d, großes/kleines griechisches Delta -> Unterschied? fummi Verfasst am: 06. Jul 2008 12:36 Titel: d, großes/kleines griechisches Delta -> Unterschied? |
 |
|
Hi,
ich hab mal ne recht blöde Frage 
Und zwar würde mich einfach mal interessieren, wo genau der Unterschied zwischen beispielsweise dU,  U und U und 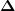 U liegt U liegt 
Hab schon nen Physikstudenten im vierten Semester gefragt, aber der konnte mir das auch nicht wirklich erklären, sondern meinte nur, dass man auch ohne das zu Wissen arbeiten kann 
Danke schonmal  |
|
 |
noob
Gast
|
 noob Verfasst am: 06. Jul 2008 14:35 Titel: noob Verfasst am: 06. Jul 2008 14:35 Titel: |
 |
|
Hallo,
ich würde sagen, dass das in erster Linie mal einfach nur Platzhalter für irgend etws sind. Nicht mehr und nicht weniger. Es haben sich gewissen Regeln etabliert, die man auch brechen kann.
So ist das grosse Delta meist eine Differenz, muss es aber nicht sein, das kleine Delta ist meist entweder das Kronecker Delta, oder eine Variation, wie zum Beispiel im Hamilton Prinzip, oder das Symbol für den Deltapeak und unser schreibschrift d steht eigentlich fast immer für totales differential.
Müsste man aber auch alles anders definieren können, aber warum sollte man das, wenn fast die gesamte Literatur so arbeitet.
In meinem Theoretischen Physik Buch gibt es kein F für Kraft, sonder X und der Impuls ist nicht P, sondern G. Warum auch immer 
Sind eben nur Zeichen, denen man den Sinn im Kontext gibt.
Gruß |
|
 |
bishop
Moderator

Anmeldungsdatum: 19.07.2004
Beiträge: 1133
Wohnort: Heidelberg
|
 bishop Verfasst am: 06. Jul 2008 15:02 Titel: bishop Verfasst am: 06. Jul 2008 15:02 Titel: |
 |
|
also das kleine delta ist kein Diffential, es beschreibt nur eine unendlich kleine Größe. Das große Delta beschreibt hingegen eine tatsächliche Differenz a-b
so ungefähr ist das^^
_________________
Ein Physiker ist jemand, der über die ersten drei Terme einer divergenten Reihe mittelt |
|
 |
noob
Gast
|
 noob Verfasst am: 06. Jul 2008 15:30 Titel: noob Verfasst am: 06. Jul 2008 15:30 Titel: |
 |
|
| bishop hat Folgendes geschrieben: | also das kleine delta ist kein Diffential, es beschreibt nur eine unendlich kleine Größe. Das große Delta beschreibt hingegen eine tatsächliche Differenz a-b
so ungefähr ist das^^ |
aber auch das ist doch wieder nur Definitionssache, oder?
Ich habe schon oft nur ein d für Differential gesehen, ohne einen Nenner, sprich auch kein echter Differentialquotienten, aber der Tutor hat es als totale Ableitung bezeichnet, obwohl nur ein einzelnes d davor stand.
Gruß |
|
 |
bishop
Moderator

Anmeldungsdatum: 19.07.2004
Beiträge: 1133
Wohnort: Heidelberg
|
 bishop Verfasst am: 06. Jul 2008 15:44 Titel: bishop Verfasst am: 06. Jul 2008 15:44 Titel: |
 |
|
puh ja, die Notation ist leider nicht wirklich allgemeingut.
Es ist z.B in der Thermodynamik so, dass man gerne das delta benutzt um anzuzeigen, dass es sich dabei nicht um ein vollständiges Differential handelt (im falle der Arbeit ist es nämlich i.A kein solches) sondern einfach eine unendlich klene größe.
Weiterhin werden im Falle der analytischen Mechanik mit dem kleinen delta virtuelle verrückungen angezeigt, die auch keine differentiale sind, sondern unendlich kleine verschiebungen
aber alles sehr schwammig in der Notation leider gottes
_________________
Ein Physiker ist jemand, der über die ersten drei Terme einer divergenten Reihe mittelt |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 06. Jul 2008 16:30 Titel: dermarkus Verfasst am: 06. Jul 2008 16:30 Titel: |
 |
|
Einverstanden, das 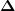 , das , das 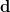 und das und das  verwendet man so: verwendet man so:
-
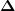 bezeichnet eine Differenz, die endlich groß ist. Zum Beispiel bezeichnet eine Differenz, die endlich groß ist. Zum Beispiel 
-
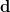 bezeichnet ebenfalls eine Differenz, aber eine sehr kleine Differenz. Die ist so klein, dass sie in Ableitungen vorkommt, in denen ja bekanntlich unendlich klein werdende Differenzen verwendet werden. bezeichnet ebenfalls eine Differenz, aber eine sehr kleine Differenz. Die ist so klein, dass sie in Ableitungen vorkommt, in denen ja bekanntlich unendlich klein werdende Differenzen verwendet werden.
Dass  ist, hast du bestimmt schon mal beim Kennenlernen der Differentialrechnung in der Schule gesehen. ist, hast du bestimmt schon mal beim Kennenlernen der Differentialrechnung in der Schule gesehen.
Weil diese unendlich kleine Differenz  in Ableitungen vorkommt, kann man sie integrieren. Deshalb nennt man sie ein Differential. in Ableitungen vorkommt, kann man sie integrieren. Deshalb nennt man sie ein Differential.
-
 bezeichnet ebenfalls eine Differenz, die unendlich klein werden kann. Allerdings sagt das bezeichnet ebenfalls eine Differenz, die unendlich klein werden kann. Allerdings sagt das  nicht, dass das ein Differential ist. Also verwendet man das nicht, dass das ein Differential ist. Also verwendet man das  zum Beispiel in der Thermodynamik für Differenzen, die sehr klein sein können, aber von denen man nicht weiß, ob man sie integrieren kann, oder von denen man weiß, dass man sie nicht integrieren kann, dass sie also kein Differential sind. zum Beispiel in der Thermodynamik für Differenzen, die sehr klein sein können, aber von denen man nicht weiß, ob man sie integrieren kann, oder von denen man weiß, dass man sie nicht integrieren kann, dass sie also kein Differential sind.
In der Thermodynamik-Vorlesung wirst du dementsprechend Schreibweisen wie  oder oder  kennenlernen, die kennzeichnen, ob es sich um ein Differential handelt oder nicht. kennenlernen, die kennzeichnen, ob es sich um ein Differential handelt oder nicht.
Also zusammengefasst:
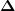 für endlich große Differenzen für endlich große Differenzen
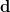 für unendlich kleine Differenzen, die Differentiale sind für unendlich kleine Differenzen, die Differentiale sind
 für unendlich kleine Differenzen, die keine Differentiale zu sein brauchen. für unendlich kleine Differenzen, die keine Differentiale zu sein brauchen. |
|
 |
bishop
Moderator

Anmeldungsdatum: 19.07.2004
Beiträge: 1133
Wohnort: Heidelberg
|
 bishop Verfasst am: 06. Jul 2008 17:53 Titel: bishop Verfasst am: 06. Jul 2008 17:53 Titel: |
 |
|
dazu natürlich noch das  , wir sprechen es "del" aus, das die partielle Ableitung kennzeichnet , wir sprechen es "del" aus, das die partielle Ableitung kennzeichnet
Scheint aber kein griechischer Buchstabe zu sein
_________________
Ein Physiker ist jemand, der über die ersten drei Terme einer divergenten Reihe mittelt |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 06. Jul 2008 17:56 Titel: dermarkus Verfasst am: 06. Jul 2008 17:56 Titel: |
 |
|
| bishop hat Folgendes geschrieben: | | Scheint aber kein griechischer Buchstabe zu sein |
Einverstanden. Dieses stilisierte d für partielle Ableitungen kenne ich unter dem "Fachbegriff" Schweinekringel  |
|
 |
DerMoment1608
Gast
|
 DerMoment1608 Verfasst am: 09. Mai 2012 16:42 Titel: DerMoment1608 Verfasst am: 09. Mai 2012 16:42 Titel: |
 |
|
|
Auch wenn der Post schon älter ist: Vielen Dank für die tolle Erklärung der ganzen verschiedenen "ds" und "deltas", das hat mich immer ziemlich verwirrt. |
|
 |
fips
Gast
|
 fips Verfasst am: 27. März 2014 09:20 Titel: d und Delta fips Verfasst am: 27. März 2014 09:20 Titel: d und Delta |
 |
|
|
Der so bezeichnete Schweinekringel ist ein Altdeutsches d |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 27. März 2014 11:16 Titel: Jayk Verfasst am: 27. März 2014 11:16 Titel: |
 |
|
War das wirklich nötig, diesen Post auszukramen?  ist ein Del. Damit bezeichnet man entweder die partielle Ableitung oder den Rand einer Mannigfaltigkeit. Laut Wikipedia wurde das Symbol zuerst von Legendre benutzt, daher würde ich doch bezweifeln, dass es sich um ein altdeutsches d handelt. Die Herkunft des Scheinekringels wird wohl für immer ungeklärt bleiben. ist ein Del. Damit bezeichnet man entweder die partielle Ableitung oder den Rand einer Mannigfaltigkeit. Laut Wikipedia wurde das Symbol zuerst von Legendre benutzt, daher würde ich doch bezweifeln, dass es sich um ein altdeutsches d handelt. Die Herkunft des Scheinekringels wird wohl für immer ungeklärt bleiben. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
|
 |
|



















