| Autor |
Nachricht |
Nighel123
Anmeldungsdatum: 14.04.2012
Beiträge: 126
|
 Nighel123 Verfasst am: 19. Nov 2012 22:02 Titel: Laplace \phi(r)=-4 pi delta(x) Nighel123 Verfasst am: 19. Nov 2012 22:02 Titel: Laplace \phi(r)=-4 pi delta(x) |
 |
|
Moin,
ich kann mir die 4 pi bei einer Umformung nicht verstehen... vielleicht könnt ihr mir ja da weiter helfen:
Siehe Anhang:
| Beschreibung: |
|
| Dateigröße: |
41.05 KB |
| Angeschaut: |
36495 mal |

|
| Beschreibung: |
|

Download |
| Dateiname: |
Screen Shot 2012-11-19 at 21.59.59.jpg |
| Dateigröße: |
45.27 KB |
| Heruntergeladen: |
2025 mal |
|
|
 |
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
 pressure Verfasst am: 22. Nov 2012 09:27 Titel: pressure Verfasst am: 22. Nov 2012 09:27 Titel: |
 |
|
Du bist offensichtlich über eine mögliche Darstellung der Delta-Distribution gestolpert:
)
Wenn du nachvollziehen willst, warum das "=" gilt, dann müsstest du dir alle Eigenschaften, welche man an die Delta-Distribution stellt, aufschreiben und einzeln nachprüfen.
Wenn du dich nur an dem  störst, dann setzt z.B. störst, dann setzt z.B.  und integriere beide Seiten über das Volumen einer im Ursprung zentrierten Kugel mit Radius R > 0, wobei für die rechte Seite der Satz von Gauß die Rechnung beschleunigt. und integriere beide Seiten über das Volumen einer im Ursprung zentrierten Kugel mit Radius R > 0, wobei für die rechte Seite der Satz von Gauß die Rechnung beschleunigt.
|
|
 |
Nighel123
Anmeldungsdatum: 14.04.2012
Beiträge: 126
|
 Nighel123 Verfasst am: 22. Nov 2012 15:19 Titel: Nighel123 Verfasst am: 22. Nov 2012 15:19 Titel: |
 |
|
also wenn ich laplace zwei mal auf das potential wirken lasse erhalte doch nach der poissongleichung

ist mein rho jetzt nicht quasi die delta verteilung? Weil sich die ladung nur an einem Punkt konzentriert. Und die 4 pi müssen noch dazu kommen, weil sich sonst nicht die 4 pi unterm bruchstrich die vor der eckigen klammer sind wegkürzen würden und damit die poissongleichung verletzt wäre... Kann man sich das so denken?
Gruß Nickel
|
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 23. Nov 2012 00:38 Titel: jh8979 Verfasst am: 23. Nov 2012 00:38 Titel: |
 |
|

<br />
)
Diese Gleichung ist eine rein mathematische Gegebenheit, die man (leicht) beweisen kann. Das hat nichts damit zu tun, dass man es in der Physik verwendet (am physikalischen Beispiel kann man es sich hoechstens veranschaulichen).
Zum Beweis wieso das so ist:
1.) Zeigen dass die linke Seite Null ist fur r!=0.
2.) Zeigen das Integration ueber ein Gebiet dass den Ursprung enthält nicht Null ergibt. Am zweckmaessigsten nimmt man dafuer -wie schon gesagt- eine Kugel mit Mittelpunkt im Ursprung.
|
|
 |
Nighel123
Anmeldungsdatum: 14.04.2012
Beiträge: 126
|
 Nighel123 Verfasst am: 23. Nov 2012 01:34 Titel: Nighel123 Verfasst am: 23. Nov 2012 01:34 Titel: |
 |
|
Moin,
ok wenn ich das jetzt versuche dann komme ich mit
^{3/2}}+\frac{y d_y}{\left(x^2+y^2+z^2\right)^{3/2}}+\frac{z d_z}{\left(x^2+y^2+z^2\right)^{3/2}}=\frac{3}{\left(x^2+y^2+z^2\right)^{3/2}})
Wie kann ich das auf 0 für alle r!=0 bekommen?
Gruß Nickel
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18065
|
 TomS Verfasst am: 23. Nov 2012 01:52 Titel: TomS Verfasst am: 23. Nov 2012 01:52 Titel: |
 |
|
Was rechnest du da? Du musst schon Zähler und Nenner differenzieren
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Nighel123
Anmeldungsdatum: 14.04.2012
Beiträge: 126
|
|
 |
kingcools
Anmeldungsdatum: 16.01.2011
Beiträge: 700
|
 kingcools Verfasst am: 23. Nov 2012 17:50 Titel: kingcools Verfasst am: 23. Nov 2012 17:50 Titel: |
 |
|
|
Ich vermute er will nur sagen, dass in diesem Problem die Richtung unwichtig ist und nur der Abstand relevant.
|
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 24. Nov 2012 08:08 Titel: jh8979 Verfasst am: 24. Nov 2012 08:08 Titel: |
 |
|
Wenn es Dich gluecklicher macht
 = \overset{\rightharpoonup }{r})
Er rechnet einfach den allgemeinen Fall vor...
|
|
 |
Nighel123
Anmeldungsdatum: 14.04.2012
Beiträge: 126
|
 Nighel123 Verfasst am: 24. Nov 2012 21:37 Titel: Nighel123 Verfasst am: 24. Nov 2012 21:37 Titel: |
 |
|
danke jetzt bin ich glücklich
und wenn jetzt

dann kommt da unendlich raus. Und das ist jetzt die definition von der Delta Funktion?
Gruß Nickel
|
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 24. Nov 2012 22:28 Titel: jh8979 Verfasst am: 24. Nov 2012 22:28 Titel: |
 |
|
| Nighel123 hat Folgendes geschrieben: |
und wenn jetzt

dann kommt da unendlich raus. Und das ist jetzt die definition von der Delta Funktion?
|
Nicht ganz. Die Delta "Funktion" ist eigentlich eine Distribution und keine regulaere Funktion. Die definierenden Eigenschaften sind
 f(x) = \begin{cases}
<br />
0 & \text{,falls } 0 \notin \Omega \\
<br />
f(0) & \text{,falls } 0 \in \Omega
<br />
\end{cases}
<br />
)
wobei  ein Gebiet in R^n ist und f eine Testfunktion. Dies klingt sehr formal ist aber einfacher als Du denkst, stell es Dir einfach als normales Integral ueber Funktionen vor. ein Gebiet in R^n ist und f eine Testfunktion. Dies klingt sehr formal ist aber einfacher als Du denkst, stell es Dir einfach als normales Integral ueber Funktionen vor.
Die erste Eigenschaft ist bei Dir erfuellt, da du gezeigt hast, dass fuer r ungleich 0, der Ausdruck Null ist. Jetzt musst Du nur noch zeigen, dass die zweite Eigenschaft erfuellt ist. Der formale mathematische Beweis ist nicht sehr schwer, erfordert aber ein wenig Nachdenken und nicht nur Rechnen. Um ein Gefuehl dafuer zu kriegen kannst Du einfach mal f(x) =1 fuer alle x setzen und gucken, dass wirklich 1 rauskommt, wenn man das Integral ausfuehrt.
|
|
 |
Nighel123
Anmeldungsdatum: 14.04.2012
Beiträge: 126
|
 Nighel123 Verfasst am: 25. Nov 2012 00:35 Titel: Nighel123 Verfasst am: 25. Nov 2012 00:35 Titel: |
 |
|
Moin,
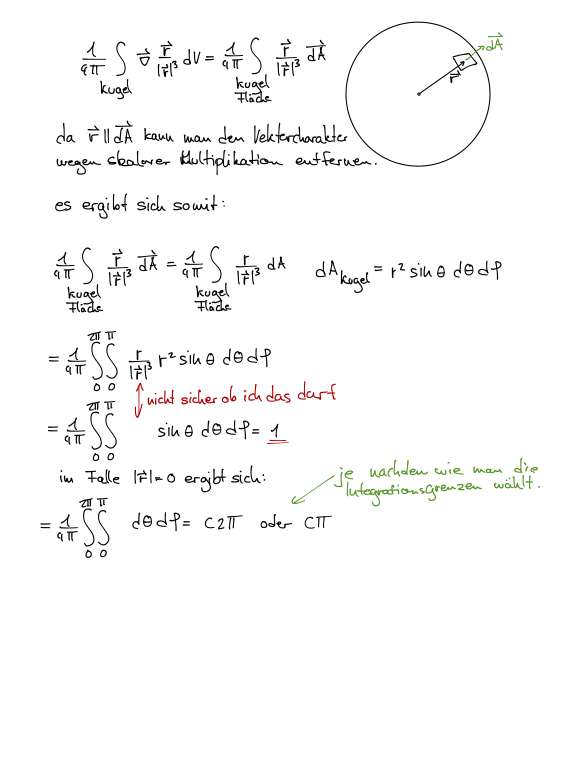
hab noch mal ein bisschen rumprobiert und mal die linke seite über eine Kugel integriert.(siehe Anhang)
bie mir kommt allerdings dann nicht das selbe wie wenn ich die delta Funktion integriere raus...:S irgendwas verstehe ich da noch nicht ganz.
Gruß Nickel
| Beschreibung: |
|
| Dateigröße: |
55.3 KB |
| Angeschaut: |
36325 mal |

|
|
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 25. Nov 2012 01:05 Titel: jh8979 Verfasst am: 25. Nov 2012 01:05 Titel: |
 |
|
(Abgesehen davon dass man das r^2 nicht so wegkuerzen kann wie Du es getan hast:)
Der Trick ist, nicht 0 Einzusetzen fuer alle Werte r!=0, sondern den Gaussen Satz anzuwenden (wir machen uns jetzt mal keine Gedanken über die genauen mathematischen Vorrauseztungen des Gauss'schen Satze, sondern wenden ihn einfach an).

fuer ein Vektorfeld F.
Hier sieht man dann auch den Grund warum man eine Kugel waehlen sollte: Dann ist dS ~ e_r.
PS: Eigentlich ist dies ein wenig geschummelt, denn es ist nicht klar, dass man den Gauss'schen Satz so ohne weiteres anwenden darf, da unser Vektorfeld divergiert fuer r -> 0. Einen sauberen mathematischen Beweis findest Du hier unter "Proof of Green function of ∇2":
http://en.citizendium.org/wiki/Green%27s_function#Proof_of_Green_function_of_.E2.88.87sup.3E2.3C.2Fsup.3E
|
|
 |
Nighel123
Anmeldungsdatum: 14.04.2012
Beiträge: 126
|
 Nighel123 Verfasst am: 26. Nov 2012 17:44 Titel: Nighel123 Verfasst am: 26. Nov 2012 17:44 Titel: |
 |
|
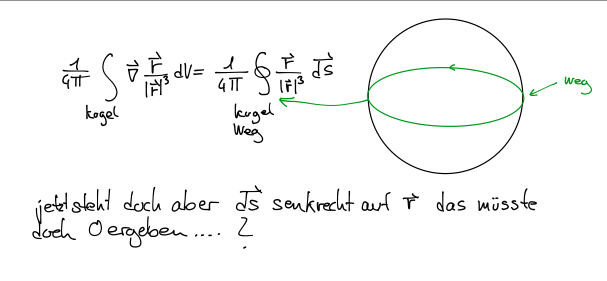
ich verstehe aber nicht ganz was ich jetzt mit dem Wegintegral machen soll. Das ist doch immer 0 weil r senkrecht zu ds steht. Und wenn r=0 dann ist das auch 0...
Bild(siehe Anhang)
| Beschreibung: |
|
| Dateigröße: |
38.21 KB |
| Angeschaut: |
36298 mal |
|
|
|
 |
kingcools
Anmeldungsdatum: 16.01.2011
Beiträge: 700
|
 kingcools Verfasst am: 26. Nov 2012 18:47 Titel: kingcools Verfasst am: 26. Nov 2012 18:47 Titel: |
 |
|
|
außer im nullpunkt ja
|
|
 |
Nighel123
Anmeldungsdatum: 14.04.2012
Beiträge: 126
|
 Nighel123 Verfasst am: 26. Nov 2012 20:43 Titel: Nighel123 Verfasst am: 26. Nov 2012 20:43 Titel: |
 |
|
|
warum im Nullpunkt nicht wenn ich einen 0 Vector auf einen anderen Projeziere und die Porjektion mit der länge des andern Vekors multipliziere bekomme ich doch auch 0 oder nicht?
|
|
 |
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
 pressure Verfasst am: 26. Nov 2012 20:55 Titel: pressure Verfasst am: 26. Nov 2012 20:55 Titel: |
 |
|
|
Das ist übrigens kein Wegintegral sondern ein Oberflächenintegral und der Vektor steht eben auch normal zur Oberfläche der Kugel, also verschwindet das Integral nicht.
|
|
 |
kingcools
Anmeldungsdatum: 16.01.2011
Beiträge: 700
|
 kingcools Verfasst am: 26. Nov 2012 21:05 Titel: kingcools Verfasst am: 26. Nov 2012 21:05 Titel: |
 |
|
| Nighel123 hat Folgendes geschrieben: | | warum im Nullpunkt nicht wenn ich einen 0 Vector auf einen anderen Projeziere und die Porjektion mit der länge des andern Vekors multipliziere bekomme ich doch auch 0 oder nicht? |
Im Nullpunkt ist das ganze nicht differenzierbar. Daher ist es nicht überall Null.(so wie es die Definition der Deltafunktion verlangt)
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18065
|
 TomS Verfasst am: 26. Nov 2012 21:24 Titel: TomS Verfasst am: 26. Nov 2012 21:24 Titel: |
 |
|
Betrachte mal den Ausdruck
)
mit der Heavisideschen Sprungfunktion.
Das Integral kann man zunächst einfach durch den Hauptsatz der Differential- und Integralrechnung lösen:
 = \Theta(+\infty)-\Theta(-\infty) = 1-0 = 1)
Andererseits kann man die Sprungfunktion auch differenzieren und erhält die eindimensionale Deltafunktion
 = \delta(x))
Und damit ist
 = 1)
Das ist der einfachstmögliche Fall, der mir zu dem Thema einfällt. Auch hier ist die Stufenfunktion bei x=0 nicht differenzierbar, aber im verallgemeinerten Sinn darf man das als Distribution auffassen und erhält ein vernünftiges Ergebnis.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Nighel123
Anmeldungsdatum: 14.04.2012
Beiträge: 126
|
|
 |
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
 pressure Verfasst am: 27. Nov 2012 07:17 Titel: pressure Verfasst am: 27. Nov 2012 07:17 Titel: |
 |
|
|
Du hast den Sinus weggezaubert und die Integrationsgrenzen sind natürlich fest... also was soll C?
|
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 28. Nov 2012 00:21 Titel: jh8979 Verfasst am: 28. Nov 2012 00:21 Titel: |
 |
|
|
Dein Volumen V ist eine Kugel vom Radius R, d.h. sobald Du das Volumen Integral in ein Oberflaechenintegral umschreibst, dann solltest du auch r durch R ersetzen. Und R ist natuerlich nie 0, sonst waere da ja keine Kugel, ueber die Du integriert. D.h. die letzte Zeile bei Dir macht natuerlich keinen Sinn, der Rest ist aber sonst in Ordnung und liefert ja auch das gewuenschte Ergebnis.
|
|
 |
Br0t
Anmeldungsdatum: 23.11.2010
Beiträge: 28
|
 Br0t Verfasst am: 20. Dez 2013 21:17 Titel: Br0t Verfasst am: 20. Dez 2013 21:17 Titel: |
 |
|
@jh8979:
Ich hätte eine Frage; du meinst man darf den Gaußschen Satz nicht ohne Weiteres anwenden, weil das Potential  im Ursprung divergiert ebenso wie sein Gradient. Nach dem Wikipedia-Artikel (http://de.wikipedia.org/wiki/Gau%C3%9Fscher_Integralsatz) zum Gaußschen Satz fordert man stetige Differenzierbarkeit für das Vektorfeld, also hier im Ursprung divergiert ebenso wie sein Gradient. Nach dem Wikipedia-Artikel (http://de.wikipedia.org/wiki/Gau%C3%9Fscher_Integralsatz) zum Gaußschen Satz fordert man stetige Differenzierbarkeit für das Vektorfeld, also hier 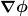 . Im Ursprung ist das hier ja eben nicht gegeben, worauf du richtigerweise hinweist. . Im Ursprung ist das hier ja eben nicht gegeben, worauf du richtigerweise hinweist.
Jetzt hast du diesen Beweis gepostet, der die Greensfunktion aus dem Greens-Theorem herleitet. Aber um das zu zeigen muss man doch eben den Gaußschen Satz bemühen, oder kennst du einen Beweis, der ohne den Gaußschen Satz auskommt? Ansonsten sehe ich keinen Vorteil dieses Beweises gegenüber dem, der sofort den Gaußschen Satz anwendet ohne sich um die Voraussetzungen zu kümmern.
Kann jemand das Problem auflösen? Warum dürfen wir den Gaußschen Satz anwenden?
|
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 20. Dez 2013 21:21 Titel: jh8979 Verfasst am: 20. Dez 2013 21:21 Titel: |
 |
|
Der "Trick" in dem geposteten Beweis ist weniger dass das Greens-Theorem angewendet wird, sondern dass der Ursprung mit einer kleinen epsilon-Kugel ausgeschnittenen wird und dann der Limes epsilon -> 0 betrachtet wird. Da man also ein Gebiet ohne eine Epsilon-Umgebung des Ursprungs betrachtet kann man die bekannten Sätze (Green, Gauss, .. ) ohne Probleme anwenden.
Zuletzt bearbeitet von jh8979 am 20. Dez 2013 22:29, insgesamt einmal bearbeitet |
|
 |
Br0t
Anmeldungsdatum: 23.11.2010
Beiträge: 28
|
 Br0t Verfasst am: 20. Dez 2013 22:07 Titel: Br0t Verfasst am: 20. Dez 2013 22:07 Titel: |
 |
|
Oh ja, ich habe den wichtigsten Punkt des Beweises beim ersten Hinschauen übersehen. Danke, das ist ein netter Trick. Die Seite ist insgesamt hilfreich.
Frohe Feiertage!
|
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 20. Dez 2013 22:28 Titel: jh8979 Verfasst am: 20. Dez 2013 22:28 Titel: |
 |
|
| Br0t hat Folgendes geschrieben: | | Frohe Feiertage! |
Ebenso 
|
|
 |
|