| Autor |
Nachricht |
Gast006
Gast
|
 Gast006 Verfasst am: 04. Dez 2020 18:14 Titel: Laplace-Transformation Gast006 Verfasst am: 04. Dez 2020 18:14 Titel: Laplace-Transformation |
 |
|
Ich habe folgende Gleichung im Bildbereich:
 = \frac{U_1}{L \cdot C} \cdot \frac{1}{s} \cdot \frac{1}{(s^2 + \frac{R}{L} \cdot s + \frac{1}{L \cdot C})} \text{ mit } L = 1 \mu H \text{ ; } R = 1 \Omega \text{ ; } C = 1\mu F )
Wie müsste ich fortfahren, damit ich es dann rücktransformieren kann.
Ich habe versucht das auf eine einfache Weise zu machen ohne Partialbruchzerlegung und Nullstellenausrechnen, indem ich die quadratische Ergänzung anwende.
Dann komme ich im dritten Bruch auf der rechten Seite des Gleichheitszeichens auf:
^2 + \frac{1}{LC} - \frac{R}{2L}})
Ab hier weiss ich dann nicht mehr weiter. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 04. Dez 2020 19:07 Titel: TomS Verfasst am: 04. Dez 2020 19:07 Titel: |
 |
|
Wieso möchtest du keine Partialbruchzerlegung machen? Weißt du grundsätzlich, wie man Integrale mittels des Residuensatzes berechnet?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 04. Dez 2020 20:40 Titel: Re: Laplace Transformation jh8979 Verfasst am: 04. Dez 2020 20:40 Titel: Re: Laplace Transformation |
 |
|
| Gast006 hat Folgendes geschrieben: |
Wie müsste ich fortfahren, damit ich es dann rücktransformieren kann.
Ich habe versucht das auf eine einfache Weise zu machen ohne Partialbruchzerlegung und Nullstellenausrechnen, .. |
Du willst es also möglichst einfach machen, ohne die einfache Methode zu wählen? ... interessant... |
|
 |
Gast006
Gast
|
 Gast006 Verfasst am: 04. Dez 2020 21:18 Titel: Gast006 Verfasst am: 04. Dez 2020 21:18 Titel: |
 |
|
|
Die einfachste Methode wäre es so umzuformen, sodass man es mittels einer Formel aus einer Korrespondenztabelle für Laplace transformierte direkt überführen kann. Wie würde es denn mittels Partialbruchzerlegung aussehen ? |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 04. Dez 2020 21:22 Titel: jh8979 Verfasst am: 04. Dez 2020 21:22 Titel: |
 |
|
| Gast006 hat Folgendes geschrieben: | | Wie würde es denn mittels Partialbruchzerlegung aussehen ? |
Indem man die Partialabruchzerlegung ausführt... |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 04. Dez 2020 21:44 Titel: TomS Verfasst am: 04. Dez 2020 21:44 Titel: |
 |
|
| Gast006 hat Folgendes geschrieben: | | Die einfachste Methode wäre es so umzuformen, sodass man es mittels einer Formel aus einer Korrespondenztabelle für Laplace transformierte direkt überführen kann. Wie würde es denn mittels Partialbruchzerlegung aussehen ? |
Wenn man die Partialbruchzerlegung durchgeführt hat, kann man das Integral mittels Residuensatz direkt ausrechnen und benötigt keine Tabelle mehr.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Gast006
Gast
|
 Gast006 Verfasst am: 04. Dez 2020 21:45 Titel: Gast006 Verfasst am: 04. Dez 2020 21:45 Titel: |
 |
|
Ich hätte doch bei der Partialbruchzerlegung:
^2 + \frac{1}{L C} - \frac{R}{2L}} = \frac{A}{(s + \frac{R}{2L})^2} + \frac{B}{(s + \frac{R}{2L})} + \frac{C}{\frac{1}{LC} - \frac{R}{2L}}) oder muss ich noch die oder muss ich noch die 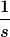 vor den Bruch, in den Nenner rein multiplizieren also: vor den Bruch, in den Nenner rein multiplizieren also:
^2 + s(\frac{1}{LC} - \frac{R}{2L})} = \frac{A}{s} + \frac{B}{(s + \frac{R}{2L})^2} + \frac{C}{s + \frac{R}{2L}} + \frac{D}{s(\frac{1}{LC} - \frac{R}{2L})})
Ist denn der Ansatz so korrekt ? |
|
 |
Gast006
Gast
|
 Gast006 Verfasst am: 04. Dez 2020 21:49 Titel: Gast006 Verfasst am: 04. Dez 2020 21:49 Titel: |
 |
|
|
Vorhin dachte ich an etwas ohne Partialbruchzerlegung. Also erweitern des Bruchs mit 1 und so weiter |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 05. Dez 2020 08:46 Titel: TomS Verfasst am: 05. Dez 2020 08:46 Titel: |
 |
|
Das wird zu kompliziert.
Gehen wir mal von deinem ursprünglichen Bruch
 = \frac{U_1}{L \cdot C} \cdot \frac{1}{s} \cdot \frac{1}{(s^2 + \frac{R}{L} \cdot s + \frac{1}{L \cdot C})} )
Er ist von der Form
 = \frac{1}{s} \frac{1}{s^2 + bs + c})
Dafür erhalte ich
 = \frac{1}{cs} - \frac{s + b}{s^2 + bs + c})
Nun bestimmst du die beiden Nullstellen für den Nenner des zweiten Bruchs, d.h.
(s - s_2))
Damit erhältst du zwei weitere Partialbruchzerlegungen
(s - s_2)} = \frac{b}{(s_1 - s_2)(s - s_1)} - \frac{b}{(s_1 - s_2)(s - s_2)} )
(s - s_2)} = \frac{s_1}{(s_1 - s_2)(s - s_1)} - \frac{s_2}{(s_1 - s_2)(s - s_2)} )
Damit kannst du die Rücktransformation aus der Tabelle ablesen.
Alternative: Für die Rücktransformation berechnest du ja
 = \frac{1}{2\pi i} \int_{\gamma -i\infty}^{\gamma + i\infty} ds \, e^{st} \, F(s))
Dabei ist gamma so zu wählen, dass die Integration rechts der Polstellen von F(s) verläuft. Die drei Polstellen n = 0,1,2 hast du oben berechnet bzw. kannst sie direkt ablesen:

Aufgrund der exponentiellen Dämpfung kannst du das Integral entlang eines Halbkreises im negativ unendlichen schließen, d.h. du erhältst
 = \frac{1}{2\pi i} \oint_Cds \, e^{st} \, F(s))
wobei die Kurve C entgegen des Uhrzeigersinns alle Polstellen umschließt.
Damit wiederum kannst du direkt den Residuensatz anwenden, d.h.
 = \frac{1}{2\pi i} \oint_Cds \, e^{st} \, F(s) = \sum_n \text{Res}_n \, e^{st} F(s) )
Da F(s) drei Polstellen erster Ordnung enthält, gilt für jedes drei Residuen n = 0,1,2
 = \lim_{s \to s_n} (s - s_n) \, e^{st} \, F(s) )
Du kannst also auf die Partialbruchzerlegung verzichten, wenn du den Residuensatz verstehst:
 = \frac{1}{(s - s_0) (s - s_1) (s - s_2)} )
 = \frac{1}{2\pi i} \oint_Cds \, e^{st} \, F(s) = \sum_n \text{Res}_n \, e^{st} F(s) )
 = \lim_{s \to s_n} (s - s_n) \, \frac{e^{st}}{(s - s_0) (s - s_1) (s - s_2)} = \frac{e^{s_nt}}{ (s_n - s_p) (s - s_q)} )
Wenn n=0, dann p=1, q=2, wenn n=1, dann p=0, q=2 usw.
Im Grenzwert kürzt sich der Vorfaktor mit s_n ja immer gegen eine der drei Polstellen 0,1,2 weg. Je Residuum n verbleiben also gerade die beiden anderen Polstellen p,q ungleich n.
Die Formel funktioniert auch für andere Zähler, insbs. wenn F(s) Polynome in s enthält.
Dieser Weg ohne Partialbruchzerlegung ist oft deutlich sparsamer.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Gast006
Gast
|
 Gast006 Verfasst am: 05. Dez 2020 11:53 Titel: Gast006 Verfasst am: 05. Dez 2020 11:53 Titel: |
 |
|
Wie kommst du denn von :
| TomS hat Folgendes geschrieben: |
 = \frac{1}{s} \frac{1}{s^2 + bs + c})
|
auf
| TomS hat Folgendes geschrieben: |
 = \frac{1}{cs} - \frac{s + b}{s^2 + bs + c})
|
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 05. Dez 2020 18:33 Titel: TomS Verfasst am: 05. Dez 2020 18:33 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
 = \frac{1}{cs} - \frac{s + b}{s^2 + bs + c})
|
Sorry, es muss natürlich
 = \frac{1}{cs} - \frac{s + b}{c(s^2 + bs + c)})
lauten, sonst kürzen sich die Terme nicht weg.
Der Ansatz ist aber klar, oder?
Jeder der beiden Brüche hat mindestens ein Polynom von Grad Null im Zähler, d.h. eine Konstante. Der Nenner mit s^2 bringt jedoch eine Potenz mehr in s mit als der andere, deswegen muss der entsprechende Zähler ein Polynom von Grad Eins statt Null haben, sonst könnten sich die Terme nicht kürzen.
D.h.

kann nicht funktionieren; stattdessen

_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Gast006
Gast
|
 Gast006 Verfasst am: 06. Dez 2020 04:05 Titel: Gast006 Verfasst am: 06. Dez 2020 04:05 Titel: |
 |
|
Ich komme dann auf:
 = U_1(s) \cdot (\frac{1}{s} - \frac{s}{s^2 + \frac{R}{L}s + \frac{1}{LC}})) Wie müsste es weiter gehen ? In der Tabelle findet man für Wie müsste es weiter gehen ? In der Tabelle findet man für  die Heaviside Funktion die Heaviside Funktion |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 06. Dez 2020 08:30 Titel: TomS Verfasst am: 06. Dez 2020 08:30 Titel: |
 |
|
| Gast006 hat Folgendes geschrieben: |
 = U_1(s) \cdot (\frac{1}{s} - \frac{s}{s^2 + \frac{R}{L}s + \frac{1}{LC}})) |
Wieso steht hier auf einmal eine Funktion U_1(s)?! Ich dachte, das wäre eine Konstante.
| Gast006 hat Folgendes geschrieben: | | Wie müsste es weiter gehen ? |
s.o.: mittels Nullstellenbestimmung für den zweiten Bruch.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Gast006
Gast
|
 Gast006 Verfasst am: 06. Dez 2020 15:37 Titel: Gast006 Verfasst am: 06. Dez 2020 15:37 Titel: |
 |
|
Ah Jo
da war ich wohl etwas zu schnell beim abtippen.
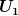 soll das hier natürlich heissen. soll das hier natürlich heissen.
Bei der Nullstellenbestimmung des zweiten Bruchs, komme ich da auf:
 = U_1 \cdot (\frac{1}{s} + \frac{s}{(s - (500 + j \cdot 866)k \frac{1}{s}) \cdot (s - (500 - j \cdot 866)k \frac{1}{s})}))
Müsste ich hier nicht nochmal eine Partialbruchzerlegung machen und dann mittels Abdeckregel einen der Koeffizienten bestimmen und der andere Koeffizient wäre dann das Konjugiert komplexe von dem anderen Koeffizient ? |
|
 |
Gast006
Gast
|
 Gast006 Verfasst am: 06. Dez 2020 15:41 Titel: Gast006 Verfasst am: 06. Dez 2020 15:41 Titel: |
 |
|
|
die 1/s hat nichts mit dem Input im Bildbereich zu tun. Es ist die Einheit 1/s bzw. die frequenz. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 06. Dez 2020 16:12 Titel: TomS Verfasst am: 06. Dez 2020 16:12 Titel: |
 |
|
Jetzt verstehe ich gar nichts mehr.
Was soll “die 1/s hat nichts mit dem Input im Bildbereich zu tun” bedeuten? Ist jetzt 1/s als Funktion Teil des Ausdrucks oder nicht?
Hast du oben gesehen, dass im zweiten Bruch ein (b+s) im Zähler steht, nicht nur ein s?
Warum setzt du jetzt Zahlen ein? Das ist doch verfrüht.
Warum fragst du, ob du nochmal Partialbruchzerlegung anwenden sollst? Ich hatte dir doch oben explizit erklärt, wie das mit Partialbruchzerlegung funktioniert - oder wie du es alternativ berechnen kannst.
Verstehst du meine Rechnung oben?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Gast006
Gast
|
 Gast006 Verfasst am: 06. Dez 2020 16:25 Titel: Gast006 Verfasst am: 06. Dez 2020 16:25 Titel: |
 |
|
Du hast doch gesagt das ich da die Nullstellen bestimmen soll, ob ich da jetzt Werte einsetze oder nicht, sollte doch nichts kaputt machen, wenn man es mit einer Formel aus der Korrespondenztabelle vergleichen möchte.
Wenn du den Residuensatz meinst - den hatten wir noch nicht, deswegen verstehe ich deine Rechnung auch nicht. |
|
 |
Gast006
Gast
|
 Gast006 Verfasst am: 06. Dez 2020 16:26 Titel: Gast006 Verfasst am: 06. Dez 2020 16:26 Titel: |
 |
|
|
Die Partialbruchzerlegung habe ich da schon gemacht. |
|
 |
Gast006
Gast
|
 Gast006 Verfasst am: 06. Dez 2020 16:37 Titel: Gast006 Verfasst am: 06. Dez 2020 16:37 Titel: |
 |
|
Ich habe da natürlich die Nullstellen eingesetzt. Ich hätte das so hinschreiben können, wie du das hingeschrieben hast:
 = U_1 \cdot (\frac{1}{s} + \frac{s}{(s - s_1) (s - s_2)}))
mit s1 und s2 sind komplex |
|
 |
Gast006
Gast
|
 Gast006 Verfasst am: 06. Dez 2020 19:35 Titel: Gast006 Verfasst am: 06. Dez 2020 19:35 Titel: |
 |
|
|
Wie gehts denn hier weiter ? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 06. Dez 2020 19:37 Titel: TomS Verfasst am: 06. Dez 2020 19:37 Titel: |
 |
|
Ich meinte natürlich, du sollst die zweite Partialbruchzerlegung durchführen - in deinem Nenner steht immer noch ein Produkt - und anschließend das Ganze als Summe dreier Brüche ohne Einsetzen von Zahlenwerten hinschreiben; auch die Rücktransformation solltest du ohne Einsetzen durchführen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Gast006
Gast
|
 Gast006 Verfasst am: 06. Dez 2020 20:01 Titel: Gast006 Verfasst am: 06. Dez 2020 20:01 Titel: |
 |
|
Ich schreibs mal ausführlich:
Also Ausgehend von dem Bruch:
(s - s_2)})
Der Ansatz:
(s - s_2)} = \frac{A}{s - s_1} + \frac{B}{s - s_2})
Hier kann ich ja mittels Abdeckregel die beiden Koeffizienten s1 und s2 bestimmen. Da aber s1 das komplex konjugierte von s2 und umgekehrt ist, kann ich ja einfach sagen das der andere Koeffizient, dass komplex konjugierte davon ist Also:
Für:
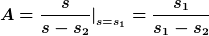
und 
Dann komme ich auf folgende Partialbrüche:
 = U_1 \cdot (\frac{1}{s} + \frac{\left(\frac{s_1}{s_1 - s_2}\right)}{s_1 - s_2} + \frac{\left(\frac{s_2}{s_2 - s_1}\right)}{s_2 - s_1}) )
Ist das so richtig ?
Das sieht mir noch komplizierter aus als davor. |
|
 |
Gast006
Gast
|
 Gast006 Verfasst am: 06. Dez 2020 20:04 Titel: Gast006 Verfasst am: 06. Dez 2020 20:04 Titel: |
 |
|
|
Ich meine A und B bestimmen s1 und s2 sind ja schon bestimmt |
|
 |
Gast006
Gast
|
 Gast006 Verfasst am: 06. Dez 2020 20:09 Titel: Gast006 Verfasst am: 06. Dez 2020 20:09 Titel: |
 |
|
 = U_1 \cdot (\frac{1}{s} + \frac{\left(\frac{s_1}{s_1 - s_2}\right)}{s - s_1} + \frac{\left(\frac{s_2}{s_2 - s_1}\right)}{s - s_2}))
sollte das heissen. |
|
 |
Gast006
Gast
|
 Gast006 Verfasst am: 06. Dez 2020 20:17 Titel: Gast006 Verfasst am: 06. Dez 2020 20:17 Titel: |
 |
|
|
Also ich sehe noch nicht, dass die hinteren 2 Partialbrüche mit den Formeln aus der Korrespondenztabelle ähneln. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
|
 |
Gast006
Gast
|
 Gast006 Verfasst am: 06. Dez 2020 20:44 Titel: Gast006 Verfasst am: 06. Dez 2020 20:44 Titel: |
 |
|
Ich hab da jetzt folgendes raus:
 = U_1 \cdot (\frac{1}{s} + (\frac{s_1}{s_1 - s_2}) \cdot \frac{1}{s + (-s_1)} + (\frac{s_2}{s_2 - s_1}) \cdot \frac{1}{s + (-s_2)}))
und das jetzt transformiert für  : :
 = U_1 \cdot (1 + (\frac{s_1}{s_1 - s_2})\cdot {e}^{+s_1 t} + \frac{s_2}{s_2 - s_1} {e}^{+s_2 t}))
Ist das so gemeint ? |
|
 |
Gast006
Gast
|
 Gast006 Verfasst am: 06. Dez 2020 21:09 Titel: Gast006 Verfasst am: 06. Dez 2020 21:09 Titel: |
 |
|
|
Wie kann ich denn die Nullstellenbestimmung allgemein halten, ohne einen Wert einzusetzen ? |
|
 |
Gast006
Gast
|
 Gast006 Verfasst am: 07. Dez 2020 02:11 Titel: Gast006 Verfasst am: 07. Dez 2020 02:11 Titel: |
 |
|
Habs jetzt raus:
Für den Fall das die Nullstellen komplex sind habe folgendes raus:
 = U_1 \cdot \left(1 + \frac{a}{\beta} \cdot {e}^{-a t} \cdot \sin(\beta t) - {e}^{-a t} \cdot \cos(\beta t) \right))
Nach der Rücktransformation habe ich die komplexen Nullstellen eingesetzt sprich ohne Werte in der folgenden Form:
^{2} - \frac{1}{LC}})
Nachdem ich festgestellt habe das }^{2}) ist, habe ich den Realteil = a und den Imaginärteil = ist, habe ich den Realteil = a und den Imaginärteil = 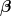 gesetzt. gesetzt.
Anschließend habe ich das so umgeformt, sodass ich einmal den komplexen sinus und einmal den komplexen kosinus ablesen konnte.
Jetzt habe ich auch verstanden, warum ich mit den Werten erst bis nach der Rücktransformation warten soll.
Danke |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 07. Dez 2020 09:12 Titel: TomS Verfasst am: 07. Dez 2020 09:12 Titel: |
 |
|
Ich hab’ das jetzt nicht im Detail durchgerechnet, vom Prinzip her sieht das jedoch vernünftig aus. Die letzte Erkenntnis ist wichtig - Einsetzen immer möglichst spät ;-)
Zum Residuensatz: falls du öfters mit Laplacetransformation zu tun hast, solltest du ihn auf jeden Fall anwenden können.
1) Im Falle von gebrochen-rationalen Funktionen F(s) mit Polynomen P(s), Q(s)
 = \frac{P(s)}{Q(s)})
sparst du dir ‘zig Seiten komplizierter Partialbruchzerlegung; das einzige, was du benötigst ist die Zerlegung von Q(s) nach den Nullstellen.
2) Außerdem kannst du damit Integrale für allgemeinere Funktionen
 = \frac{f(s)}{Q(s)})
lösen, wobei f(s) eine nahezu beliebige Funktion ist - während du mit konventionellen Methoden keine Chance hast.
Ich würde mal behaupten, dass der Residuensatz in weiten Bereichen der theoretischen Physik das mit großem Abstand wichtigste mathematische Hilfsmittel ist, um eine Vielzahl von Berechnungen deutlich schneller oder überhaupt ausführen zu können.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Gast006
Gast
|
 Gast006 Verfasst am: 07. Dez 2020 14:40 Titel: Gast006 Verfasst am: 07. Dez 2020 14:40 Titel: |
 |
|
|
Also ich gehe gerade den Residuensatz durch und stelle fest, dass dieser sehr viel rechenintensiver ist als die Partialbruchzerlegung mit anschließender Korrespondenztabelle. Vielleicht ist der Residuensatz für einfache und mehrfache Pole von einfachen Termen im rellen ganz gut geeignet aber sinnvoll ist der in dieser Aufgabe eher weniger, wenn man auf die Zeit achtet und die hat man in Prüfungen ehh zu wenig |
|
 |
Gast006
Gast
|
 Gast006 Verfasst am: 07. Dez 2020 14:57 Titel: Gast006 Verfasst am: 07. Dez 2020 14:57 Titel: |
 |
|
|
Kommt drauf an wo man in der Physik ist. In der Elektrotechnik wird schon ganz gerne auf Korrespondenztabellen zurückgegriffen. Kenne jetzt auch niemanden der Schaltvorgänge mit dem Residuensatz gelöst hat. In der theoretischen Elektrotechnik mag es da sicher einige Bereiche geben oder halt in der theoretischen Physik. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 07. Dez 2020 15:44 Titel: TomS Verfasst am: 07. Dez 2020 15:44 Titel: |
 |
|
| Gast006 hat Folgendes geschrieben: | | Also ich gehe gerade den Residuensatz durch und stelle fest, dass dieser sehr viel rechenintensiver ist als die Partialbruchzerlegung mit anschließender Korrespondenztabelle. |
Dann hast du etwas nicht verstanden.
Du benötigst für beide Ansätze die Polstellen.
Im Falle des Residuensatz benötigst du jedoch keine Partialbruchzerlegung und keine Korrespondenztabelle, du kannst das Ergebnis oft direkt ablesen.
Ich zeig’s dir mal an einem Beispiel.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Gast006
Gast
|
 Gast006 Verfasst am: 07. Dez 2020 22:54 Titel: Gast006 Verfasst am: 07. Dez 2020 22:54 Titel: |
 |
|
Das Internet ist voll mit Beispielen. Wenn du ein Beispiel brauchst, nimm gleich dieses hier:
 = \frac{U_1}{L C} \cdot (\frac{1}{s(s - s_1)(s - s_2)}))
Mit  = \frac{1}{(s - 0)(s - s_1)(s - s_2)})
Dann versteh ich dich auch bzgl. dieser Aufgabe. Ich bleibe dabei.
Bei diesem Ausdruck liesst man weder den sinus noch den cosinus direkt ab, noch ist es einfacher bzw. schneller wie mit ohne Anwendung von Formeln aus Korrespondenztabellen.
Darauf war mein vorheriger Kommentar bezogen. Das man im nachhinein die Partialbruchzerlegung gespart hat mag durchaus sein, jedoch bringt es nichts, wenn ich dadurch mehr Seiten für Umformungsschritte aufgewendet habe. |
|
 |
Gast006
Gast
|
 Gast006 Verfasst am: 07. Dez 2020 23:07 Titel: Gast006 Verfasst am: 07. Dez 2020 23:07 Titel: |
 |
|
|
Es gibt hierbei auch Formeln aus Korrespondenztabellen, die ganz ohne Partialbruchzerlegung an der Stelle auskommen. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 07. Dez 2020 23:22 Titel: jh8979 Verfasst am: 07. Dez 2020 23:22 Titel: |
 |
|
Ich halte die Partialbruchzerlegung für "einfacher", weil man weniger verstanden haben muss, aber der Residuensatz ist einfach sehr machtvoll und macht die Rechnung in der Tat simpel (, sofern man weiss, was man hier tut  ). ).
Wenn ich das hier
| TomS hat Folgendes geschrieben: |
 = \frac{1}{2\pi i} \oint_Cds \, e^{st} \, F(s) = \sum_n \text{Res}_n \, e^{st} F(s) )
|
einfach anwende
| Gast006 hat Folgendes geschrieben: | Wenn du ein Beispiel brauchst, nimm gleich dieses hier:
 = \frac{U_1}{L C} \cdot (\frac{1}{s(s - s_1)(s - s_2)}))
Mit  = \frac{1}{(s - 0)(s - s_1)(s - s_2)})
|
kann ich ohne Nachdenken ablesen:
 = \frac{U_1}{L C} \cdot \left( \frac{e^{0 \cdot t}}{(0 - s_1)(0 - s_2)} +\frac{e^{s_1 t}}{s_1 (s_1 - s_2)} +\frac{e^{s_2 t}}{s_2 (s_2 - s_1)} \right))
(Modulo irgendwelcher Heaviside-Thetas, die da auftauchen, wenn man vorsichtig vorgeht, aber das Problem hat die Ablese-Methode aus Tabellen aus.)
Der Rest ist dann bisschen rumspielen mit komplexen e-Funktionen.
Und wie Tom geschrieben hat, funktioniert dieser Weg immer ohne Probleme, solange ich die Nullstellen des Nenners kenne, egal wie der Zähler aussieht. |
|
 |
Multiple_Choice
Anmeldungsdatum: 08.04.2019
Beiträge: 77
|
 Multiple_Choice Verfasst am: 08. Dez 2020 00:00 Titel: Multiple_Choice Verfasst am: 08. Dez 2020 00:00 Titel: |
 |
|
Soweit war ich ja auch bereits mit dem Resiudensatz gekommen. Wenn ich aber das so haben will, dass ich weder Partialbruchzerlegung, noch das vereinfachen der e-Funktionen zu sin und cos haben möchte, dann habe ich folgende Korrespondenztabelle, die mir bei komplexen Nullstellen auf der Seite 4 Formel Nr. 56, die direkte Lösung beinhaltet:
http://eitidaten.fh-pforzheim.de/daten/mitarbeiter/blankenbach/vorlesungen/mathe_2/mathe_2_Laplace_folien.pdf
Natürlich gibt es auch die allgemeinen Tabellen wie die auf Wikipedia aber das Verständniss von Korrespondenztabellen sollte es sein, eben so wenig wie möglich zu rechnen und eben das kann in einer Prüfung Leben retten. Beim umformen der e-Funktionen kann in einer Stress Situation wie der einer Prüfung, sich schnell mal ein Fehler einschleichen und schon hat man das ganze, in den Sand gesetzt.
Ergo, hat man die passende Tabelle zur Hand, ist man deutlich schneller am Werk als beim Residuensatz, wo man noch die e-Funktionen zu sin und cos umformen muss |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 08. Dez 2020 00:38 Titel: TomS Verfasst am: 08. Dez 2020 00:38 Titel: |
 |
|
Also wir wollen dich nicht davon überzeugen, dass du unsere Methode anwenden sollst. Gerade in der Prüfung machst du das am besten so, wie du es gewohnt bist.
Der Residuensatz ist dann vorteilhaft, wenn
i) der Nenner sehr viele Faktoren enthält und die Partialbruchzerlegung aufwändig und fehlerträchtig wird; du hast hier bereits recht lange dazu gebraucht
ii) der Zähler zusätzlich ein kompliziertes Polynom enthält, wodurch die Partialbruchzerlegung noch unübersichtlicher wird
iii) kompliziertere Funktionen als Polynome auftreten, so dass die Tabelle nicht hilft
Zur Anwendung des Residuensatzes musst du die e-Funktion nicht in Sinus und Cosinus zerlegen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 08. Dez 2020 07:16, insgesamt einmal bearbeitet |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 08. Dez 2020 01:57 Titel: jh8979 Verfasst am: 08. Dez 2020 01:57 Titel: |
 |
|
| Multiple_Choice hat Folgendes geschrieben: |
Ergo, hat man die passende Tabelle zur Hand, ist man deutlich schneller am Werk als beim Residuensatz, wo man noch die e-Funktionen zu sin und cos umformen muss |
Ja, natürlich: wenn ich die Lösungen schon bereit habe zum Ablesen, dann ist das offensichtlich die schnellste Variante... |
|
 |
Gast006
Gast
|
 Gast006 Verfasst am: 08. Dez 2020 15:35 Titel: Gast006 Verfasst am: 08. Dez 2020 15:35 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
Zur Anwendung des Residuensatzes musst du die e-Funktion nicht in Sinus und Cosinus zerlegen. |
Das stimmt schon alles was du sagst. Jedoch macht der Ausdruck, so mit den e-Funktionen keinen Sinn, wenn man eine trifftige Aussage z.B über den Schaltvorgang treffen muss.
Erst wenn ich die e-Funktionen zu sin und cos Funktionen gebastelt habe, kann ich über den Schaltvorgang des RLC Schwingkreises in der Prüfung eine Aussage treffen.
Bei der Partialbruchzerlegung kann man sich da natürlich vieles verhauen aber sobald man dahinter gekommen ist, dass man erst bis zum Schluss mit dem einsetzen warten muss, ist das Thema auch kein Problem mehr. Beim Residuensatz ist das ja nämlich auch so.
Nichts desto trotz war das eine sehr interessante Session und hab den Residuensatz gelernt. Danke |
|
 |
|

 ).
).