| Autor |
Nachricht |
KleinerWicht
Gast
|
 KleinerWicht Verfasst am: 03. März 2018 15:39 Titel: Reibungskraft zweier Kreisflächen |
 |
|
Meine Frage:
Wenn ich zwei Kreisflächen gegeneinander verschiebe (Radius bekannt) kann ich über einen Drehmomentschlüssel das notwendige Drehmoment messen.
Wie komme ich von dem Drehmoment (Nm) auf die Reibungskraft (N)?
Meine Ideen:
Integral der Kreisfläche? |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5867
Wohnort: jwd
|
| Mathefix Verfasst am: 03. März 2018 19:11 Titel: |
|
|
Mit N = Anpresskraft der Scheiben
 |
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5870
|
| Myon Verfasst am: 03. März 2018 19:28 Titel: Re: Reibungskraft zweier Kreisflächen |
|
|
| KleinerWicht hat Folgendes geschrieben: |
Integral der Kreisfläche? |
Ja. Wobei man etwas genauer sagen muss, was man hier unter der Reibungskraft versteht. Ist  die Reibungskraft, wenn die beiden Scheiben gegeneinander bewegt werden, so gilt für die Reibungskraft pro Fläche
Für das Drehmoment integrierst Du und erhältst (r=Radius der Scheiben):
 |
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5867
Wohnort: jwd
|
| Mathefix Verfasst am: 03. März 2018 19:46 Titel: Re: Reibungskraft zweier Kreisflächen |
|
|
| Myon hat Folgendes geschrieben: | | KleinerWicht hat Folgendes geschrieben: |
Integral der Kreisfläche? |
Ja. Wobei man etwas genauer sagen muss, was man hier unter der Reibungskraft versteht. Ist die Reibungskraft, wenn die beiden Scheiben gegeneinander bewegt werden, so gilt für die Reibungskraft pro Fläche
Für das Drehmoment integrierst Du und erhältst (r=Radius der Scheiben):
|
Ich dachte, dass die Reibkraft unabhängig von der Auflagefläche ist. |
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5870
|
| Myon Verfasst am: 03. März 2018 19:50 Titel: Re: Reibungskraft zweier Kreisflächen |
|
|
| Mathefix hat Folgendes geschrieben: | | Ich dachte, dass die Reibkraft unabhängig von der Auflagefläche ist. |
Das Drehmoment pro Fläche nimmt linear mit dem Radius zu. Die Gleichung M=F_R*r würde gelten, wenn die Scheiben sich nur am Rand berühren würden. |
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5867
Wohnort: jwd
|
| Mathefix Verfasst am: 04. März 2018 12:23 Titel: Re: Reibungskraft zweier Kreisflächen |
|
|
| Myon hat Folgendes geschrieben: | | Mathefix hat Folgendes geschrieben: | | Ich dachte, dass die Reibkraft unabhängig von der Auflagefläche ist. |
Das Drehmoment pro Fläche nimmt linear mit dem Radius zu. Die Gleichung M=F_R*r würde gelten, wenn die Scheiben sich nur am Rand berühren würden. |
Alles klar. Hätte ich ich auch durch reines Nachdenken drauf kommen müssen: Angriffspunkt der Reibkraft liegt im Flächenschwerpunkt des durch das Drehmoment aufgespannten Dreiecks.
Wünsche Dir einen schönen Sonntag.
Gruss
Jörg |
|
|
KleinerWicht
Gast
|
| KleinerWicht Verfasst am: 04. März 2018 12:55 Titel: Irgendwas passt nicht |
|
|
Die Ergebnisse passen nicht.
Ich gehe daher mal etwas tiefer in die Hintergründe. Wenn man einen Boden bei unterschiedlichen Normalkräften abscherrt, dann kann man die Scherfestigkeit in Reibungswinkel und Kohäsion zerlegen.
Mein erster Versuchsaufbau arbeitete mit zwei Kästen, welche gegeneinander verschoben werden. Mit dem Aufbringen einer Last und Messung der notwendigen Zugkraft konnte ich die Schubspannung (Zugkraft je Fläche) ermitteln und gegen die Normalspannung (Last auf Fläche) auftragen. Die Ergebnisse waren für kohäsionsarme Stoffe (z.b. Sand) plausibel. Bei kohäsiven Stoffen ergab sich das Problem, dass sich die Fläche durch den Schub verkleinert und ich somit auch den Schubweg messen müsste.
Um dies zu vermeiden war der Gedanke zwei Zylinder gegeneinander zu verdrehen. Die Normalspannung ergibt sich wieder über Last und Fläche. Mit Hilfe eines Drehmomentschlüssels bzw. einen Hebelarm und einen Kraftmesser kann ich das notwendige Drehmoment zum Abscheren ermitteln. Die Fläche bleibt hierbei konstant.
Die berechneten Scherkräfte passen jedoch nicht, sie sind deutlich zu klein.
Es muss ein Integral für die Scherkraft in Abhängigkeit von Drehmoment und Kreisfläche geben? |
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5867
Wohnort: jwd
|
| Mathefix Verfasst am: 04. März 2018 13:33 Titel: Re: Irgendwas passt nicht |
|
|
| KleinerWicht hat Folgendes geschrieben: | Die Ergebnisse passen nicht.
Ich gehe daher mal etwas tiefer in die Hintergründe. Wenn man einen Boden bei unterschiedlichen Normalkräften abscherrt, dann kann man die Scherfestigkeit in Reibungswinkel und Kohäsion zerlegen.
Mein erster Versuchsaufbau arbeitete mit zwei Kästen, welche gegeneinander verschoben werden. Mit dem Aufbringen einer Last und Messung der notwendigen Zugkraft konnte ich die Schubspannung (Zugkraft je Fläche) ermitteln und gegen die Normalspannung (Last auf Fläche) auftragen. Die Ergebnisse waren für kohäsionsarme Stoffe (z.b. Sand) plausibel. Bei kohäsiven Stoffen ergab sich das Problem, dass sich die Fläche durch den Schub verkleinert und ich somit auch den Schubweg messen müsste.
Um dies zu vermeiden war der Gedanke zwei Zylinder gegeneinander zu verdrehen. Die Normalspannung ergibt sich wieder über Last und Fläche. Mit Hilfe eines Drehmomentschlüssels bzw. einen Hebelarm und einen Kraftmesser kann ich das notwendige Drehmoment zum Abscheren ermitteln. Die Fläche bleibt hierbei konstant.
Die berechneten Scherkräfte passen jedoch nicht, sie sind deutlich zu klein.
Es muss ein Integral für die Scherkraft in Abhängigkeit von Drehmoment und Kreisfläche geben? |
Diese komplexen Zusammenhänge hast Du in Deiner Ursprungsfrage nicht erwähnt. Es treten also nicht nur Reib-, sondern auch Scherkräfte auf.
Völlig anderer Belastungsfall. |
|
|
KleinerWicht
Gast
|
| KleinerWicht Verfasst am: 05. März 2018 20:16 Titel: Wieso anderer Belastungsfall |
|
|
Ich verstehe nicht wieso das in andere Fall ist? Ist doch Wurst ob es eine Reibungskraft, Scherkraft oder sonst was für eine Kraft ist.
Ich muss jedesmal von einem Drehmoment und einer Kreisfläche auf die Kraft zurückrechnen?! |
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5867
Wohnort: jwd
|
| Mathefix Verfasst am: 06. März 2018 14:16 Titel: Re: Wieso anderer Belastungsfall |
|
|
| KleinerWicht hat Folgendes geschrieben: | Ich verstehe nicht wieso das in andere Fall ist? Ist doch Wurst ob es eine Reibungskraft, Scherkraft oder sonst was für eine Kraft ist.
Ich muss jedesmal von einem Drehmoment und einer Kreisfläche auf die Kraft zurückrechnen?! |
Drehmoment = Kraft x Hebelarm (Kraftangriffspunkt)
Der Angriffspunkt der Scherkraft ist mit Sicherheit von dem der Reibkraft verschieden. |
|
|
Duke711
Anmeldungsdatum: 26.01.2017
Beiträge: 434
|
| Duke711 Verfasst am: 06. März 2018 14:44 Titel: |
|
|
|
Bei kohäsiven Stoffen hast Du dann aber eine zusätzliche Abscherrung, das hat dann aber nichts mehr mit dem Coulombschen Reibgesetz zu tun, also ein völlig anderer Ansatz. |
|
|
KleinerWicht
Gast
|
| KleinerWicht Verfasst am: 10. März 2018 12:49 Titel: Unterschied - und nun? |
|
|
| Duke711 hat Folgendes geschrieben: | | Bei kohäsiven Stoffen hast Du dann aber eine zusätzliche Abscherrung, das hat dann aber nichts mehr mit dem Coulombschen Reibgesetz zu tun, also ein völlig anderer Ansatz. |
Ich habe doch auch Kohäsion zwischen zwei Holzscheiben?
Aber gut, und nun, hat jemand einen Lösungansatz? |
|
|
KleinerWicht
Gast
|
| KleinerWicht Verfasst am: 10. März 2018 13:07 Titel: Re: Reibungskraft zweier Kreisflächen |
|
|
| Myon hat Folgendes geschrieben: |
|
Mit dem Umstellen nach F erhalte ich
Dann passen die Ergebnisse schon besser, aber Perfekt passen würden sie mit einem Faktor von 2 statt 1,5.
Stimmt dae Integral vielleicht nicht? |
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5867
Wohnort: jwd
|
| Mathefix Verfasst am: 10. März 2018 19:02 Titel: Re: Reibungskraft zweier Kreisflächen |
|
|
| KleinerWicht hat Folgendes geschrieben: | | Myon hat Folgendes geschrieben: |
|
Mit dem Umstellen nach F erhalte ich
Dann passen die Ergebnisse schon besser, aber Perfekt passen würden sie mit einem Faktor von 2 statt 1,5.
Stimmt dae Integral vielleicht nicht? |
Das Endergebnis stimmt.
Im Zwischenergebnis fehlt der Faktor f
 |
|
|
GustavGans
Gast
|
| GustavGans Verfasst am: 10. März 2018 19:32 Titel: |
|
|
|
Vielleicht hast du in deinem Versuchsaufbau auf irgendeine Lagerreibung vergessen. Ich nehme an du hast eine Vorrichtung für deinen Versuch gebaut. |
|
|
Duke711
Anmeldungsdatum: 26.01.2017
Beiträge: 434
|
| Duke711 Verfasst am: 11. März 2018 02:00 Titel: Re: Unterschied - und nun? |
|
|
| KleinerWicht hat Folgendes geschrieben: | | Duke711 hat Folgendes geschrieben: | | Bei kohäsiven Stoffen hast Du dann aber eine zusätzliche Abscherrung, das hat dann aber nichts mehr mit dem Coulombschen Reibgesetz zu tun, also ein völlig anderer Ansatz. |
Ich habe doch auch Kohäsion zwischen zwei Holzscheiben?
Aber gut, und nun, hat jemand einen Lösungansatz? |
Wo hast Du da bitte Kohäsion? Kohäsion beschreibt den inneren Zusammenhalt eines Stoffes. Nur handelt es sich bei von einenander getrennten Holzscheiben nun nicht mehr um einen einzelnen Stoff. Adhäsion ja, aber bei zwei Holzscheiben verschwinden gering klein, auf jeden keine Erklärung warum das Coulombschen Reibgesetz nicht stimmen sollte.
Nur hast Du sicher nicht alle Effekte betrachtet und das mathematische Modell unbewusst sehr vereinfacht. |
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5867
Wohnort: jwd
|
| Mathefix Verfasst am: 11. März 2018 12:21 Titel: |
|
|
Die Diskussion dreht sich im Kreis.
Der Ansatz von Myon über die Reibung stellt ein zulässig vereinfachtes Modell dar, da die Mikrostruktur und deren Kraftwirkung an der Kontaktfläche nicht bekannt ist.
Für die Reibkraft gilt
m = Masse Scheibe
Der Betrag von 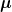 hängt von der Rauhtiefe der Scheiben (Mikrostruktur) ab. Unter ihm kann man alle Einflussfaktoren subsummieren.
Bei bekanntem Drehmoment kann 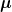mit der Myon´schen Formel bestimmt werden. Dann passt alles. |
|
|
KleinerWicht
Gast
|
| KleinerWicht Verfasst am: 17. März 2018 08:39 Titel: Torsion, nicht Reibung |
|
|
Ich habe den Denkfehler jetzt verstanden.
Es gibt bei dem Versuch zwei Zustände.
Phase 1: Durch das Drehmoment wird die kohäsive Probe verzerrt, bis es zu einem Bruch kommt. Kurz vor dem Bruch habe ich die maximale Scherspannung erreicht.
Phase 2: Durch das Drehmoment werden zwei Probenhälften entlang der Bruchfläche verschoben, es wirkt nur noch eine Reibungskraft.
Oder? |
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5867
Wohnort: jwd
|
| Mathefix Verfasst am: 17. März 2018 13:58 Titel: Re: Torsion, nicht Reibung |
|
|
| KleinerWicht hat Folgendes geschrieben: | Ich habe den Denkfehler jetzt verstanden.
Es gibt bei dem Versuch zwei Zustände.
Phase 1: Durch das Drehmoment wird die kohäsive Probe verzerrt, bis es zu einem Bruch kommt. Kurz vor dem Bruch habe ich die maximale Scherspannung erreicht.
Phase 2: Durch das Drehmoment werden zwei Probenhälften entlang der Bruchfläche verschoben, es wirkt nur noch eine Reibungskraft.
Oder? |
Es existieren nicht 2 getrennte Phasen, sondern es besteht ein kontinuierlicher Prozess. Mit steigender Anzahl von Umdrehungen, weden die Unebenheiten immer mehr abgeschliffen und damit sinkt die Reibungskraft. |
|
|
|
Registrieren
Login
FAQ
Suchen
