| Autor |
Nachricht |
Hilfe Feuer et brennt
Gast
|
 Hilfe Feuer et brennt Verfasst am: 12. Dez 2013 16:14 Titel: Kurzfrage lineare DGL 2. Ordnung harmonischer Oszillator Hilfe Feuer et brennt Verfasst am: 12. Dez 2013 16:14 Titel: Kurzfrage lineare DGL 2. Ordnung harmonischer Oszillator |
 |
|
Meine Frage:
Hallo kurz Frage:
Es geht um die DGL für den harmonischen Oszillator.
Wir haben die DGL:
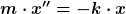
 (1) (1)
Es ist jetzt allgemein üblich 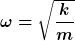 zu verwenden. Dadurch solle die Sache übersichtlicher werden. zu verwenden. Dadurch solle die Sache übersichtlicher werden.
(1) ist eine homogene lineare DGL zweiter Ordnung mit konstanten Koeffizienten. Wie kommt man auf die charakteristische Gleichung:

??? Das ist mir ein Rätsel.
\cdot (D- \omega \cdot i))
Die Eigenwerte kann man jetzt ablesen.
Meine Ideen:
Mir ist halt unklar wie man von den obigen Gleichungen, auf diese kommt:

Ich quäle mich schon so lange diesen Umformungsschritt zu verstehen, sodass ich jetzt hier an Euch weitergebe. Es wäre mir wirklich sehr wichtig wenn mir jemand diesen Sachverhalt erklären könnte.
Grüße ganz herzlich Dennis. |
|
 |
Wiktoria
Gast
|
 Wiktoria Verfasst am: 12. Dez 2013 16:30 Titel: Re: Kurzfrage lineare DGL 2. Ordnung harmonischer Oszillator Wiktoria Verfasst am: 12. Dez 2013 16:30 Titel: Re: Kurzfrage lineare DGL 2. Ordnung harmonischer Oszillator |
 |
|
| Hilfe Feuer et brennt hat Folgendes geschrieben: | Hallo kurz Frage:
Es geht um die DGL für den harmonischen Oszillator.
Wir haben die DGL:
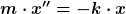 |
Kurze Antwort: das ist keine Gleichung einer harmonischen Schwingung!
m ... Masse
k ... Federkonstante |
|
 |
Hilfe Feuer et brennt
Gast
|
 Hilfe Feuer et brennt Verfasst am: 12. Dez 2013 16:33 Titel: Hilfe Feuer et brennt Verfasst am: 12. Dez 2013 16:33 Titel: |
 |
|
Ja falsch ausgedrückt, das folgt aus dem zweiten Newtonschen Axiom. Aber kannst du mir bitte bei meiner Frage helfen?
Dennis |
|
 |
Wiktoria
Gast
|
 Wiktoria Verfasst am: 12. Dez 2013 16:37 Titel: Wiktoria Verfasst am: 12. Dez 2013 16:37 Titel: |
 |
|
|
Was ist denn die Frage? |
|
 |
Hilfe Feuer et brennt
Gast
|
 Hilfe Feuer et brennt Verfasst am: 12. Dez 2013 16:41 Titel: Re: Kurzfrage lineare DGL 2. Ordnung harmonischer Oszillator Hilfe Feuer et brennt Verfasst am: 12. Dez 2013 16:41 Titel: Re: Kurzfrage lineare DGL 2. Ordnung harmonischer Oszillator |
 |
|
| Hilfe Feuer et brennt hat Folgendes geschrieben: | Meine Frage:
Hallo kurz Frage:
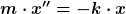
 (1) (1)
|
Wie komme von dieser Gleichung.
Zu dieser Gleichung:
| Hilfe Feuer et brennt hat Folgendes geschrieben: | Meine Frage:

|
Dennis |
|
 |
Wiktoria
Gast
|
 Wiktoria Verfasst am: 12. Dez 2013 16:45 Titel: Wiktoria Verfasst am: 12. Dez 2013 16:45 Titel: |
 |
|
Dies halte ich für unmöglich.
Vielleicht kann jemand anders helfen. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 12. Dez 2013 16:48 Titel: jh8979 Verfasst am: 12. Dez 2013 16:48 Titel: |
 |
|
|
Du nimmst als Ansatz für Deine Lösung x(t)=e^(D*t). Einsetzen liefert Dir dann statt einer DGL für x(t) eine algebraische Gleichung in D. |
|
 |
Hilfe Feuer et brennt
Gast
|
 Hilfe Feuer et brennt Verfasst am: 12. Dez 2013 16:50 Titel: Hilfe Feuer et brennt Verfasst am: 12. Dez 2013 16:50 Titel: |
 |
|
Dort habe ich es z.B. gefunden aber auch woanders:
Da ich keine Links eintippen kann: Auf google und dann folgendes eingeben: harmonischer oszillator charakteristisches Polynom und direkt erster Treffer (Matheplanet)
Direkt oben nach den ersten Diagrammen.
Dennis |
|
 |
Hilfe Feuer et brennt
Gast
|
 Hilfe Feuer et brennt Verfasst am: 12. Dez 2013 17:00 Titel: Hilfe Feuer et brennt Verfasst am: 12. Dez 2013 17:00 Titel: |
 |
|
| jh8979 hat Folgendes geschrieben: | | Einsetzen liefert Dir dann statt einer DGL für x(t) eine algebraische Gleichung in D. |
=e^{D\cdot t})
Kann noch nicht verstehen wie man damit auf:
 kommt. kommt.
Danke.
Dennis. |
|
 |
Wiktoria
Gast
|
 Wiktoria Verfasst am: 12. Dez 2013 17:03 Titel: Wiktoria Verfasst am: 12. Dez 2013 17:03 Titel: |
 |
|
|
Und ebenfalls rätselhaft: wie kommt man von k auf D? |
|
 |
stereo
Anmeldungsdatum: 27.10.2008
Beiträge: 402
|
 stereo Verfasst am: 12. Dez 2013 17:09 Titel: stereo Verfasst am: 12. Dez 2013 17:09 Titel: |
 |
|
| Hilfe Feuer et brennt hat Folgendes geschrieben: | | jh8979 hat Folgendes geschrieben: | | Einsetzen liefert Dir dann statt einer DGL für x(t) eine algebraische Gleichung in D. |
=e^{D\cdot t})
Kann noch nicht verstehen wie man damit auf:
 kommt. kommt.
Danke.
Dennis. |
=A e^{D\cdot t})
=D A e^{D\cdot t} = D x(t))
=D^2 A e^{D\cdot t} = D^2 x(t))
Das in die DGL einsetzen und schauen und fertig. |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 12. Dez 2013 17:12 Titel: Jayk Verfasst am: 12. Dez 2013 17:12 Titel: |
 |
|
Die charakteristische Gleichung bekommst du, wenn du einen Exponentialansatz machst:  Wie Richard Feynman gesagt hat (so ähnlich): Auf diese Weise haben wir das Ableiten auf eine Multiplikation reduziert. Dann kannst du statt Wie Richard Feynman gesagt hat (so ähnlich): Auf diese Weise haben wir das Ableiten auf eine Multiplikation reduziert. Dann kannst du statt  schreiben schreiben  x = 0) . Merkst du was? . Merkst du was? |
|
 |
Hilfe Feuer et brennt
Gast
|
 Hilfe Feuer et brennt Verfasst am: 12. Dez 2013 17:21 Titel: Hilfe Feuer et brennt Verfasst am: 12. Dez 2013 17:21 Titel: |
 |
|
| stereo hat Folgendes geschrieben: |
=A e^{D\cdot t})
=D A e^{D\cdot t} = D x(t))
=D^2 A e^{D\cdot t} = D^2 x(t))
Das in die DGL einsetzen und schauen und fertig. |
Das ist klar. Das Problem ist noch wo ist dann bei der Gleichung:

das m und x hin?
Danke Euch riesig für die Antworten!
Dennis |
|
 |
stereo
Anmeldungsdatum: 27.10.2008
Beiträge: 402
|
 stereo Verfasst am: 12. Dez 2013 17:29 Titel: stereo Verfasst am: 12. Dez 2013 17:29 Titel: |
 |
|
Das sollte eigentlich nicht schwer sein:



Jetzt einsetzen:
 = 0)
Da die triviale Lösung x(t)=0 wahrscheinlich nicht gesucht ist, muss die Summe Null werden. |
|
 |
Hilfe Feuer et brennt
Gast
|
 Hilfe Feuer et brennt Verfasst am: 12. Dez 2013 17:44 Titel: Hilfe Feuer et brennt Verfasst am: 12. Dez 2013 17:44 Titel: |
 |
|
Das da ist jetzt klar. In meinem Fall fehlt da aber noch ein Vorfaktor:
- - > w w w .fotos-hochladen.net/view/bild38vncghkz1q.png<- -
Dennis |
|
 |
stereo
Anmeldungsdatum: 27.10.2008
Beiträge: 402
|
 stereo Verfasst am: 12. Dez 2013 17:52 Titel: stereo Verfasst am: 12. Dez 2013 17:52 Titel: |
 |
|
 , das ist genau das, was dir Jayk versucht hat zu erklären. Die Ableitungen sind nur noch Multiplikationen mit K. Und in der "nullten Ableitung" (keine Ableitung) steht eben , das ist genau das, was dir Jayk versucht hat zu erklären. Die Ableitungen sind nur noch Multiplikationen mit K. Und in der "nullten Ableitung" (keine Ableitung) steht eben  . .
Warum hast du jetzt eigentlich K mit D getauscht? |
|
 |
Hilfe Feuer et brennt
Gast
|
 Hilfe Feuer et brennt Verfasst am: 12. Dez 2013 17:57 Titel: Hilfe Feuer et brennt Verfasst am: 12. Dez 2013 17:57 Titel: |
 |
|
| Hilfe Feuer et brennt hat Folgendes geschrieben: | Dort habe ich es z.B. gefunden aber auch woanders:
Da ich keine Links eintippen kann: Auf google und dann folgendes eingeben: harmonischer oszillator charakteristisches Polynom und direkt erster Treffer (Matheplanet)
Direkt oben nach den ersten Diagrammen.
|
Das ist Notation, aber es muss ja so stimmen. Es kommt daher, dass dort (in dem Zitat beschrieben) es halt mit D gehandhabt wird.
Danke Euch vielmals.
Dennis |
|
 |
|















