| Autor |
Nachricht |
Ascareth
Anmeldungsdatum: 11.11.2010
Beiträge: 203
|
 Ascareth Verfasst am: 09. Nov 2012 21:29 Titel: Richtung beim Biegemoment am Balken Ascareth Verfasst am: 09. Nov 2012 21:29 Titel: Richtung beim Biegemoment am Balken |
 |
|
Hallo,
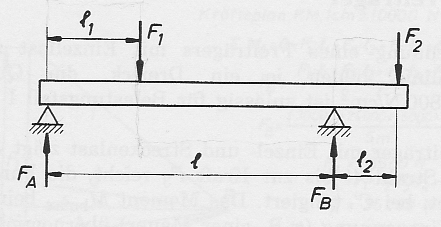
irgendwie schnall ich die Richtungsfestlegung bei den Biegemomenten am Balken nicht so richtig. Ich habe im Anhang einmal die Richtungskonvention für die folgenden Aufgaben und einmal den Lageplan für die Aufgabe selbst.
Wenn der Drehpunkt im Punkt B (Fb) liegt, ist es dann wirklich so dass man von da ab stur die Biegemomente der durch die von unten nach oben wirkenden Kräfte positiv und die der entgegengesetzt wirkenden Kräfte negativ bewertet?
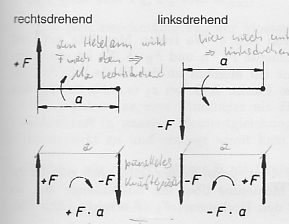
Dem Anhang Richtungsfestlegung.png entnehme ich links unten, dass eine nach unten gerichtete Kraft die rechts an einer nach oben gerichteten Kraft vorbeischert, ein positives Moment erzeugt. Demnach müsste doch das Moment das durch die Kraft F2 im Anhang aufgabe_richtung.png erzeugt wird positiv sein. Dem widerspricht aber, die Konvention der Momentrichtung von oben nach unten wirkender Kräfte. Oder?
Oder kann man generell sagen, dass für die Bewertung der äußeren Momente am Balken, die parallelen Kräftepaare gar nicht herangezogen werden? Bewertet man da also ausschließlich mit der Momentdefinition der Hebelarme?
Gruß, Asca
| Beschreibung: |
|
| Dateigröße: |
57.39 KB |
| Angeschaut: |
19607 mal |
|
| Beschreibung: |
|
| Dateigröße: |
56.78 KB |
| Angeschaut: |
19607 mal |
|
|
|
 |
Packo
Gast
|
 Packo Verfasst am: 10. Nov 2012 08:33 Titel: Packo Verfasst am: 10. Nov 2012 08:33 Titel: |
 |
|
Ich habe dir schon einmal erklärt:
Ein Biegemoment ist positiv, wenn es den Balken nach oben hohl biegt.
Die Definition: Kraft nach oben ergibt negatives, Kraft nach unten ergibt positives Biegemoment, ist Unsinn.
|
|
 |
Ascareth
Anmeldungsdatum: 11.11.2010
Beiträge: 203
|
 Ascareth Verfasst am: 10. Nov 2012 17:52 Titel: Ascareth Verfasst am: 10. Nov 2012 17:52 Titel: |
 |
|
| Packo hat Folgendes geschrieben: | Ich habe dir schon einmal erklärt:
Ein Biegemoment ist positiv, wenn es den Balken nach oben hohl biegt. |
Ich will dir das ja gern auch glauben, aber ich verstehe das nicht. Was soll das bedeuten? Soll der Balken nach oben gebogen werden, oder wie meinst du das? Dann müsste doch eine Kraft von unten wirken, was ja eben gerade positiv wäre ... Was meinst du mit "nach oben hohl biegen"? (Ein hohler Balken ist für mich ein Rohr) Oder meinst du konvex / konvert?
| Packo hat Folgendes geschrieben: |
Die Definition: Kraft nach oben ergibt negatives, Kraft nach unten ergibt positives Biegemoment, ist Unsinn. |
Wie würdest du die 4 Konvention in dem Bild beschreiben?
|
|
 |
Packo
Gast
|
 Packo Verfasst am: 10. Nov 2012 19:58 Titel: Packo Verfasst am: 10. Nov 2012 19:58 Titel: |
 |
|
Ich dachte nach oben hohl sei verständlich, ist jedoch zugegebenermaßen mathematisch nicht ganz einwandfrei.
Besser: wir zählen die x-Koordinate von links nach rechts positiv und die y-Koordinate nach oben positiv.
Ist dann die zweite Ableitung der Biegelinie nach x an einer Stelle x=x0 positiv, dann ist das Biegemoment an der Stelle x=x0 positiv.
Anmerkung: die Funktion y = x² ist hohl nach oben gekrümmt.
Englisch sagt man: "can hold water".
Die Funktion y =-x² ist hohl nach unten gekrümmt.
"cannot hold water".
(Die Bezeichnungen konkav und konvex sind ebenfalls zu vermeiden, weil auch sie verschieden definiert werden).
|
|
 |
Ascareth
Anmeldungsdatum: 11.11.2010
Beiträge: 203
|
 Ascareth Verfasst am: 11. Nov 2012 00:53 Titel: Ascareth Verfasst am: 11. Nov 2012 00:53 Titel: |
 |
|
Das heißt also das Moment das den Balken wie die Funktion y = x² hohl nach oben biegt ist positiv. Richtig?
Warum erzeugt dann Fa ein positives Moment? Fa biegt den Balken in die entgegen gesetzte Form von -x^2.
|
|
 |
Packo
Gast
|
 Packo Verfasst am: 11. Nov 2012 08:17 Titel: Packo Verfasst am: 11. Nov 2012 08:17 Titel: |
 |
|
| Ascareth hat Folgendes geschrieben: | | Warum erzeugt dann Fa ein positives Moment? Fa biegt den Balken in die entgegen gesetzte Form von -x^2. |
Die entgegengesetzte Form von -x² ist x², also positive Krümmung.
Versuch mal einen Strohhalm mit FA zu belasten!
|
|
 |
Ascareth
Anmeldungsdatum: 11.11.2010
Beiträge: 203
|
 Ascareth Verfasst am: 11. Nov 2012 18:36 Titel: Ascareth Verfasst am: 11. Nov 2012 18:36 Titel: |
 |
|
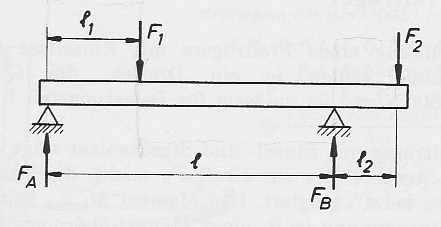
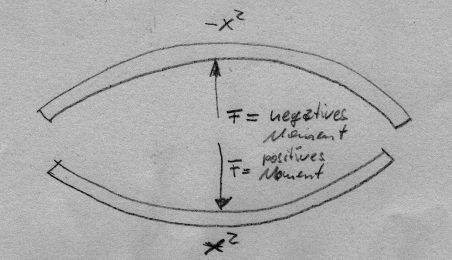
Also wie im zweiten Anhang (balken_biegemoment_vorzeichen.jpeg)?
Wenn ich diese Definition einmal auf den ersten Anhang (aufgabe_richtung_611.png) beziehe, dann sieht das bei mir so aus:
Fa = negativ, F1 = positiv, Fb = Drehpunkt, F2 = positiv
Das funktioniert so aber nicht. F2 hat zu F1 ein unterschiedliches Vorzeichen. Wieso?
| Beschreibung: |
|
| Dateigröße: |
57.39 KB |
| Angeschaut: |
19460 mal |
|
| Beschreibung: |
|
| Dateigröße: |
21.96 KB |
| Angeschaut: |
19472 mal |
|
|
|
 |
Packo
Gast
|
 Packo Verfasst am: 11. Nov 2012 21:09 Titel: Packo Verfasst am: 11. Nov 2012 21:09 Titel: |
 |
|
| Ascareth hat Folgendes geschrieben: | Fa = negativ, F1 = positiv, Fb = Drehpunkt, F2 = positiv
Das funktioniert so aber nicht. F2 hat zu F1 ein unterschiedliches Vorzeichen. Wieso? |
Du scheinst da Kräfte mit Biegemomenten zu verwechseln.
Wir habe das Vorzeichen von Biegemomenten definiert, nicht das Vorzeichen von Kräften.
|
|
 |
Ascareth
Anmeldungsdatum: 11.11.2010
Beiträge: 203
|
 Ascareth Verfasst am: 11. Nov 2012 22:30 Titel: Ascareth Verfasst am: 11. Nov 2012 22:30 Titel: |
 |
|
Wenn ein Biegemoment mit F * l berechnet wird, wie soll dann die Kraft ein dem Biegemoment unterschiedliches Vorzeichen haben? Das Kraft physikalisch nicht gleich einem Moment ist, ist schon klar, aber Vorzeichen müssen doch gleich sein. Oder wird hier mit negativen und positiven Längen gerechnet?
Ich glaube das führt alles zu nichts ... könntest du nicht einfach von links nach rechts darstellen an Hand welcher Kriterien du über die Vorzeichen entscheidest?
|
|
 |
Ascareth
Anmeldungsdatum: 11.11.2010
Beiträge: 203
|
 Ascareth Verfasst am: 12. Nov 2012 10:03 Titel: Ascareth Verfasst am: 12. Nov 2012 10:03 Titel: |
 |
|
Moin, ich habe noch einmal etwas gegoogelt und folgendes finden können:
http://www.maschinenbau-wissen.de/skript/mechanik/statik/59-schnittreaktionen
würdest du dem so zustimmen?
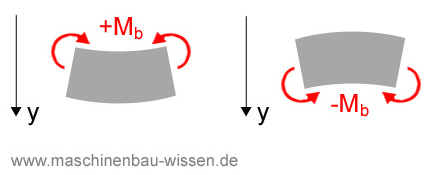
Ganz unten findet sich die Grafik im Anhang, die ganz einfach und simpel die Richtung des Momentes beschreibt.
Das gibt denke ich genau deine Definition über die Parabelöffnung wieder. +x² -> +M ; -x² -> -M
Richtig oder?
ABER: wenn ich das so anwende, dann bekomme ich für Fa * l = positiv, F1 * (l - l1) = positiv und für F2 * l2 = negativ.
Mit den Werten: F1 = 4000N; F2 = 2000N; l = 6m; l1 = 3m; l2 = 1,5m
Für Fa habe ich dann -2500N heraus ... kann ja nur falsch sein, da eine Kraft, die von unten nach oben wirkt positiv definiert ist.
| Beschreibung: |
|
| Dateigröße: |
14.39 KB |
| Angeschaut: |
19421 mal |
|
Zuletzt bearbeitet von Ascareth am 12. Nov 2012 10:38, insgesamt 3-mal bearbeitet |
|
 |
Packo
Gast
|
 Packo Verfasst am: 12. Nov 2012 10:15 Titel: Packo Verfasst am: 12. Nov 2012 10:15 Titel: |
 |
|
Wir führen ein Koordinatensystem ein mit x positiv nach rechts und x = 0 am linken Trägerende.
Wir denken uns den Träger bei x durchgeschnitten und berechen Biegemomente von allen Kräften, die links der Schnittstelle wirken.
Wir zählen Biegemomente, die im Uhrzeigersinn wirken, als positiv.
Dann erhalten wir:
Im Bereich I) 0 ≤ x ≤ L1
M(x) = FA*x
Im Bereich II) L1 ≤ x ≤ L
M(x) = FA*x - F1*(x-L1)
Im Bereich III) L ≤ x ≤ L+L2
M(x) = Fa*x - F1*(x-L1) + FB*(x-L)
An drei Stellen ist das Biegemoment gleich 0:
für x=0
für x = L+L2
für x=F1*L1/(F1-FA)
Das Biegemoment ist positiv für 0 < x < F1*L1/(F1-FA)
Das Biegemoment ist negativ für F1*L1/(F1-FA) < x < L+L2
|
|
 |
Ascareth
Anmeldungsdatum: 11.11.2010
Beiträge: 203
|
 Ascareth Verfasst am: 12. Nov 2012 11:48 Titel: Ascareth Verfasst am: 12. Nov 2012 11:48 Titel: |
 |
|
Und was bringt dir das, wenn du weder Fa noch Fb gegeben hast? Das führt dich zu einer Gleichung mit zwei Unbekannten. Du musst doch den Drehpunkt in Fa oder Fb legen, und dann dafür eine Momentengleichung aufstellen und dann nach Fa / Fb umstellen!
| Packo hat Folgendes geschrieben: | | Wir zählen Biegemomente, die im Uhrzeigersinn wirken, als positiv. |
Das ist doch verständlich. Wenn ich die Kräfte so bewerte komme ich auf folgende Momentengleichung (Drehpunkt Fb!).
M = 0 = Fa * l - F1 * (l - l1) + F2 * l2
- Fa * l = -F1 * (l - l1) + F2 * l2 | *(-1/l)
Fa = (F1 * (l - l1) - F2 * l2) / (l)
Fa = (4000N * (6m - 3m) - 2000N * 1,5m) / (6m) = 1500N
Was richtig ist! Zumindest lt. Lösung.
Dann ist doch die Definition super simpel eigentlich. Es geht also lediglich um den Uhrzeigersinn.
Allerdings! Lässt sich dann die Definition über die Zug-Druck-Verformung des Balkens nicht anwenden, da auf den Punkt Fb bezogen, die Kraft F1 oben auf den Balken eine Druckspannung wirkt, und F2, oben auf den Balken eine Zugspannung wirkt, da ja rechts von F2 kein weiteres Lager vorhanden ist. ...
Was meinst du dazu?
|
|
 |
|




















