| Autor |
Nachricht |
mzh
Anmeldungsdatum: 31.05.2010
Beiträge: 44
|
 mzh Verfasst am: 25. Jan 2011 16:33 Titel: Einheit Wellenfunktion mzh Verfasst am: 25. Jan 2011 16:33 Titel: Einheit Wellenfunktion |
 |
|
Hallo zusammen
Ich versuche mir über die Bedeutung der Integration über die Wellenfunktion klar zu werden, also bspw: 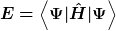 . .
Wenn man jetzt nur den Operator für die kinetische Energie betrachtet, 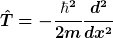 (in einer Dimension), so muss sich ja für das Integral (in einer Dimension), so muss sich ja für das Integral 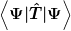 die Einheit [J] ergeben (es handelt sich ja um Energie). die Einheit [J] ergeben (es handelt sich ja um Energie).
Wenn ich die Einheiten zusammenrechne, komme ich aber auf [N].
Ausgehend davon, dass die Einheit der Wellenfunktion 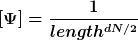 ist, wobei d die Dimensionalität und N die Anzahl Teilchen ist (hier d,N=1). ist, wobei d die Dimensionalität und N die Anzahl Teilchen ist (hier d,N=1).
Also, die Einheit von 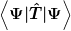 ist nun ist nun
^2}{kg}\frac{1}{m^2}\frac{1}{m^{1/2}}) . Wenn ich das zusammenfasse kriege ich aber . Wenn ich das zusammenfasse kriege ich aber 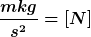 . .
Kann mir jemand erklären was ich falsch mache? Vielen Dank für Postings. |
|
 |
Chillosaurus
Anmeldungsdatum: 07.08.2010
Beiträge: 2440
|
 Chillosaurus Verfasst am: 25. Jan 2011 17:09 Titel: Chillosaurus Verfasst am: 25. Jan 2011 17:09 Titel: |
 |
|
Die Wellenfunktion hat die Dimension 1/WURZEL(Volumen)
Das Betragsquadrat hat also die Dimension 1/Volumen
Die Energie hat die Dimension einer Energie (was auch sonst?)
Unterm Integral steht Also Energie pro Volumen.
Integration über ein Volumen liefert also die Energie, wie erwartet.
In deinem 1-D-Fall ist das analog.
Dein Problem wird wohl sein, dass du für die Energie nicht die passende Einheit gewählt hast und diese aus unerklärlichem Grunde auch noch quadriert hast. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 25. Jan 2011 17:18 Titel: TomS Verfasst am: 25. Jan 2011 17:18 Titel: |
 |
|
Die Dimension und die Darstellung deines Operators der kinetischen Energie ist irreführend, denn
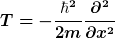
gilt genau dann, wenn T auf die Wellenfunktion in der Ortsdarstellung wirkt
 = \langle x|\psi\rangle)
nicht wenn der abstrakte Operator auf einen abstrakten Ket wirkt. Dann gilt aber für die Energie auch
\,T\,\psi(x))
und damit solltest du die Einheiten ablesen können
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
mzh
Anmeldungsdatum: 31.05.2010
Beiträge: 44
|
 mzh Verfasst am: 25. Jan 2011 22:06 Titel: mzh Verfasst am: 25. Jan 2011 22:06 Titel: |
 |
|
| Chillosaurus hat Folgendes geschrieben: | Die Wellenfunktion hat die Dimension 1/WURZEL(Volumen)
Das Betragsquadrat hat also die Dimension 1/Volumen
Die Energie hat die Dimension einer Energie (was auch sonst?)
Unterm Integral steht Also Energie pro Volumen.
Integration über ein Volumen liefert also die Energie, wie erwartet.
In deinem 1-D-Fall ist das analog.
Dein Problem wird wohl sein, dass du für die Energie nicht die passende Einheit gewählt hast und diese aus unerklärlichem Grunde auch noch quadriert hast. |
Das Quadrat kommt von h_quer^2 (im Zähler des Operators).
@tomS: Ich denke, im Sinne gewöhnlicher Quantenchemie ist es berechtigt, den Operator als auf Psi(x) in der Ortsdarstellung wirkend zu schreiben.
Ich denke mein Problem war, dass ich das dm in der Integration nicht berücksichtigt habe und deshalb [N] anstelle von [J] erhielt (besser kann ich es leider nicht erklären).
Vielen Dank für eure Beiträge. |
|
 |
Chillosaurus
Anmeldungsdatum: 07.08.2010
Beiträge: 2440
|
 Chillosaurus Verfasst am: 25. Jan 2011 22:29 Titel: Chillosaurus Verfasst am: 25. Jan 2011 22:29 Titel: |
 |
|
| mzh hat Folgendes geschrieben: | | [...] Das Quadrat kommt von h_quer^2 (im Zähler des Operators). [...] |
Wenn du mit der Einheit des Operators umgehst, musst du bedenken, dass sich dadurch auch die Einheit der Wellenfunktion ändert, auf die der Operator wirkt (durch das Ableiten)! |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 25. Jan 2011 22:35 Titel: TomS Verfasst am: 25. Jan 2011 22:35 Titel: |
 |
|
| mzh hat Folgendes geschrieben: |
@tomS: Ich denke, im Sinne gewöhnlicher Quantenchemie ist es berechtigt, den Operator als auf Psi(x) in der Ortsdarstellung wirkend zu schreiben. |
Ja, dagegen ist nichts einzuwenden.
Aber der Ausdruck
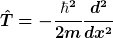
gilt eben gerade für die Ortsdarstellung und nicht für
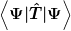
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
mzh
Anmeldungsdatum: 31.05.2010
Beiträge: 44
|
 mzh Verfasst am: 26. Jan 2011 18:18 Titel: mzh Verfasst am: 26. Jan 2011 18:18 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
Aber der Ausdruck
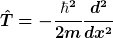
gilt eben gerade für die Ortsdarstellung und nicht für
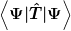 |
Wie müsste denn der Operator dann aussehen, damit er für 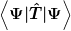 gilt? Müsste man da etwa Zeit einführen, dh. eine neue Einheit würde dazukommen.. gilt? Müsste man da etwa Zeit einführen, dh. eine neue Einheit würde dazukommen..
@chillosaurus: Ich habe mir auch gedacht, dass durch eine Operation wie Ableiten die Einheit ändert. Aber wenn ich mir das an einem Beispiel durchdenke, dann komme ich zum Schluss, dass man doch die Einheiten quasi von der Ableitung abseparieren kann.
Angenommen ich leite die Strecke nach der Zeit ab (um Geschwindigkeit zu erhalten), dann habe ich ja schon alle Einheiten der Geschwindigkeit (s/t), wenn ich die Differentiale (d, dt) einführe, da die Einheit von dt, ja [dt]=s ist, unabhängig davon wie infinitesimal klein das dt ist.
) |
|
 |
Chillosaurus
Anmeldungsdatum: 07.08.2010
Beiträge: 2440
|
 Chillosaurus Verfasst am: 26. Jan 2011 19:29 Titel: Chillosaurus Verfasst am: 26. Jan 2011 19:29 Titel: |
 |
|
Ah.. dann verstehe ich, wie du das schreibst.
Es ist doch alles richtig. Eine relevante Aussage kriegst du erst nach der Integration über das Volumen. Das Volumen ist in deinem Fall eindimensional deswegen wird aus N -Integration in 1 Dimension--> N*m, Bingo das ist eine Energie. Deine Vermutung war also korrekt. |
|
 |
mzh
Anmeldungsdatum: 31.05.2010
Beiträge: 44
|
 mzh Verfasst am: 26. Jan 2011 20:53 Titel: mzh Verfasst am: 26. Jan 2011 20:53 Titel: |
 |
|
| Chillosaurus hat Folgendes geschrieben: | Ah.. dann verstehe ich, wie du das schreibst.
Es ist doch alles richtig. Eine relevante Aussage kriegst du erst nach der Integration über das Volumen. Das Volumen ist in deinem Fall eindimensional deswegen wird aus N -Integration in 1 Dimension--> N*m, Bingo das ist eine Energie. Deine Vermutung war also korrekt. |
Hm, ich würde sagen ich stimme dem zu, allerdings würde ich es anders betonen. Die "Aussage der Wellenfunktion" ergibt sich erst, wie du sagst, aus der Integration. Die *Einheit* des Integrals 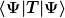 ist allerdings durch das Volumenelement der Integration von Anfang an (mit-)bestimmt, denn im eindimensionalen Fall, [dV]=m. Ich hoffe, ich mache das nicht unnötig kompliziert, wollte aber nur nochmals darauf hinweisen. ist allerdings durch das Volumenelement der Integration von Anfang an (mit-)bestimmt, denn im eindimensionalen Fall, [dV]=m. Ich hoffe, ich mache das nicht unnötig kompliziert, wollte aber nur nochmals darauf hinweisen. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 26. Jan 2011 23:28 Titel: TomS Verfasst am: 26. Jan 2011 23:28 Titel: |
 |
|
| mzh hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: |
Aber der Ausdruck
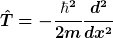
gilt eben gerade für die Ortsdarstellung und nicht für
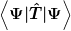 |
Wie müsste denn der Operator dann aussehen, damit er für 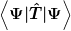 gilt? gilt? |
Hast du den Unterschied zwische der abstrakten Dirac-Notation und der Wellenfunktion verstanden? Es gilt
 = \langle x | \psi\rangle)
Du kannst auf den Ket keine x-Ableitung anwenden; die x-Abhängigkeit entsteht erst durch die Projektion auf den Bra
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
mzh
Anmeldungsdatum: 31.05.2010
Beiträge: 44
|
 mzh Verfasst am: 28. Jan 2011 09:21 Titel: mzh Verfasst am: 28. Jan 2011 09:21 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
Hast du den Unterschied zwische der abstrakten Dirac-Notation und der Wellenfunktion verstanden? Es gilt
 = \langle x | \psi\rangle)
Du kannst auf den Ket keine x-Ableitung anwenden; die x-Abhängigkeit entsteht erst durch die Projektion auf den Bra |
Ehrlich gesagt, wahrscheinlich nicht. Ich habe bis jetzt angenommen, die Dirac-Notation ist im Grunde nur eine Bequemlichkeit, um 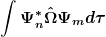 als als 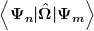 schreiben zu können. schreiben zu können.
Ich muss sagen, mir war nicht klar, dass ich mit 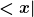 auf die Wellenfunktion wirken muss, um eine x-Abhängigkeit zu erhalten. Allerdings, jetzt wo ich darüber nachdenke, auf die Wellenfunktion wirken muss, um eine x-Abhängigkeit zu erhalten. Allerdings, jetzt wo ich darüber nachdenke,  \neq |\psi>) , von daher kann ich langsam sehen, weshalb meine erste Formulierung falsch war. , von daher kann ich langsam sehen, weshalb meine erste Formulierung falsch war. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 28. Jan 2011 09:54 Titel: TomS Verfasst am: 28. Jan 2011 09:54 Titel: |
 |
|
Diese Erkenntnis ist wichtiger als die Diskussion über Einheiten der Wellenfunktion.
Die Idee Diracs bei der Einführung der abstrakten Bras und Kets lag genau darin, eine formale Methode zu haben, die unabhängig ist von speziellen x-, p-, Energie- usw. Darstellungen. Die Idee ist eigentlich ganz einfach.
Es gibt einen abstrakten Hilbertraum von Kets; auf diesem sind Operatoren definiert. Das Skalarprodukt wird mittels der Bras aus dem Dualraum gebildet.
Spezifische Darstellungen (hier generisch a, wobei a für x, p, E usw. stehen kann) erhält man durch Projektion
 = \langle a | \psi\rangle)
Die a-Darstellung wird durch die Eigenvektoren eines hermiteschen Operators A definiert (Ortsoperator, Impulsoperator, Hamiltonoperator). Diese Eigenvektoren bilden ein (verallgemeinertes) VONS, d.h. es gilt die "Eins-Identität"
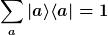
D.h. die Summe über alle Projektoren auf alle a-Eigenzustände ergibt den Eins-Operator.
Damit kann jeder Zustand geschrieben werden als
 |a\rangle)
Damit zeigt sich, dass die Wellenfunktion (mit der Variablen a) nichts weiter ist als der Entwicklunsgkoeffizient des Zustandes in der a-Darstellung. Damit sind die Fourierentwicklungen für x- und p-Darstellung nur Spezialfälle dieser verallgemeinerten Notation.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
mzh
Anmeldungsdatum: 31.05.2010
Beiträge: 44
|
 mzh Verfasst am: 28. Jan 2011 12:46 Titel: mzh Verfasst am: 28. Jan 2011 12:46 Titel: |
 |
|
 = \langle a | \psi\rangle)
Es ist für mich schon eine neue Erkenntnis, dass die Wellenfunktion erst durch Projektion von a auf das Ket "spezifisch" abhängig von a wird. Das muss ich erstmal verarbeiten. Kennst du evlt. das Buch von Szabo/Ostlund und weisst zufällig ob das dort geschildert wird? Ich muss mir das wirklich genauer anschauen. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 28. Jan 2011 12:54 Titel: TomS Verfasst am: 28. Jan 2011 12:54 Titel: |
 |
|
Das Buch kenne ich nicht.
Ein knappes aber sehr gutes Buch ist der "Sakurai"; da findest du das alles. Zum Rechnen lernen und üben ist der aber eher ungeeignet.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
mzh
Anmeldungsdatum: 31.05.2010
Beiträge: 44
|
 mzh Verfasst am: 28. Jan 2011 13:20 Titel: mzh Verfasst am: 28. Jan 2011 13:20 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Das Buch kenne ich nicht.
Ein knappes aber sehr gutes Buch ist der "Sakurai"; da findest du das alles. Zum Rechnen lernen und üben ist der aber eher ungeeignet. |
Noch was zu deinem vorletzten Post, du hast dort geschrieben, psi(a) = <a|psi>, mit a = x, p, E...
Also kann Psi von E abhängen oder fasse ich das verkehrt auf? |
|
 |
Chillosaurus
Anmeldungsdatum: 07.08.2010
Beiträge: 2440
|
 Chillosaurus Verfasst am: 28. Jan 2011 14:09 Titel: Chillosaurus Verfasst am: 28. Jan 2011 14:09 Titel: |
 |
|
| mzh hat Folgendes geschrieben: | | [...] Also kann Psi von E abhängen oder fasse ich das verkehrt auf? |
Es gibt doch zu jeder Observablen eine Darstellung der Wellenfunktion. Also ex. auch eine Energiedarstellung. |
|
 |
|















