| Autor |
Nachricht |
Langley
Anmeldungsdatum: 19.10.2010
Beiträge: 12
|
 Langley Verfasst am: 02. Nov 2010 20:33 Titel: Trichteraufgabe, wann kreist die Punktmasse? Langley Verfasst am: 02. Nov 2010 20:33 Titel: Trichteraufgabe, wann kreist die Punktmasse? |
 |
|
Die 2. Runde der Physikolympiade endete am 29. Oktober. Ich nehme an, man kann jetzt über diese Aufgaben diskutieren.
R(z) soll den Radius des Trichters als Funktion des vertikalen Abstandes zum unteren Rand beschreiben.
Einige werden sicherlich schon die Aufgabe zu Gesicht bekommen haben:
Betrachtet wird eine Punktmasse der Masse m , die sich reibungsfrei in unterschiedlichen Trichtern bewegt.
Die Masse wird mit einer Geschwindigkeit v bei einer Höhe z in den Trichter gesetzt. Überraschenderweise bleibt die Masse, unabhängig von der gewählten z-Koordinate, bei der Bewegung stets auf der gleichen Höhe, ihre z-Koordinate ist also konstant.
Bestimmen Sie, welche Form der Trichter dafür haben muss, d.h. geben Sie die Funktion R(z) in Abhängigkeit von den auftretenden Parametern an. Bestimmen Sie außerdem, wie hoch der Trichter demnach sein muss, wenn sich die Masse mit einer Geschwindigkeit von v = 1,0 m/s bewegt und der obere bzw. untere Radius des Trichters 50 cm bzw. 5,0 cm betragen.
Mein Ansatz:
Zeichnet man die Situation in einem Kräftedreieck auf ergibt sich:
 = \frac{F_{Radial}}{F_{G}} = \frac{v^2}{g \cdot r} )
wobei phi: Steigungswinkel
Desweiteren führt dies auf die Differentialgleichung:
 = \frac{v^2}{g \cdot R(z)} )
Eine Lösung der DGL ist:
 = \sqrt{2} \cdot \sqrt\frac{v^2 \cdot z}{g})
Jedoch erscheint mir diese Lösung falsch, da sie - wenn überhaupt - die Funktion z(R) beschreibt. Was habe ich falsch gemacht/übersehen?
|
|
 |
eva1
Anmeldungsdatum: 06.10.2010
Beiträge: 532
|
 eva1 Verfasst am: 03. Nov 2010 00:38 Titel: Re: Trichteraufgabe, wann kreist die Punktmasse? eva1 Verfasst am: 03. Nov 2010 00:38 Titel: Re: Trichteraufgabe, wann kreist die Punktmasse? |
 |
|
| Langley hat Folgendes geschrieben: |
 = \frac{F_{Radial}}{F_{G}} = \frac{v^2}{g \cdot r} )
 = \frac{v^2}{g \cdot R(z)} )
|
Das ist falsch, da \not= R'(z) )
Es gilt nämlich: =Z'(r))
Damit: =\frac{v^2}{g}\cdot ln(\frac{r}{r_{unten}}))
Und damit ist R:=r_{unten}\cdot e^{\frac{z\cdot g}{v^2}})
Wie geht die Aufgabe mit der Münze??
Hat da jemand eine Idee?
|
|
 |
eva1
Anmeldungsdatum: 06.10.2010
Beiträge: 532
|
 eva1 Verfasst am: 03. Nov 2010 13:25 Titel: eva1 Verfasst am: 03. Nov 2010 13:25 Titel: |
 |
|
Wie kann folgendes Problem gelöst werden?
Welche Form(Funktion R(z) Radius von Höhe z) muss ein Trichter haben, damit eine Münze (Masse m und Radius r) auf jeder höhe z nur mit einer horizontalen Geschwindigkeit v rotieren kann. Die z-Koordinate ist daher konstant. Außerdem gilt: R>>r! Das ganze ist natürlich reibungsfrei und die Münze rollt.
Meine Idee:
Kann man das mit einem Kollergang vergleichen?
|
|
 |
Langley
Anmeldungsdatum: 19.10.2010
Beiträge: 12
|
 Langley Verfasst am: 03. Nov 2010 16:22 Titel: Langley Verfasst am: 03. Nov 2010 16:22 Titel: |
 |
|
Wieso ist
} \, dz = \ln(\frac{r}{r_{unten}} ))
?
|
|
 |
eva1
Anmeldungsdatum: 06.10.2010
Beiträge: 532
|
 eva1 Verfasst am: 03. Nov 2010 18:04 Titel: eva1 Verfasst am: 03. Nov 2010 18:04 Titel: |
 |
|
} \, dz \not= \ln(\frac{r}{r_{unten}} ))
Du musst vom unteren Trichterand über den Radius integrieren.
Ergo:
)
|
|
 |
Limes90
Anmeldungsdatum: 03.11.2010
Beiträge: 39
|
 Limes90 Verfasst am: 03. Nov 2010 18:28 Titel: Limes90 Verfasst am: 03. Nov 2010 18:28 Titel: |
 |
|
ich habe die Aufgabe auch bearbeitet und erhalte für den Radius =e^{\frac{z(R) \cdot g}{v^2}}) und damit 23,5 cm für die Trichterhöhe und damit 23,5 cm für die Trichterhöhe
bei der Aufgabe mit der Münze erhalte ich einen Radius von
=e^{\frac{z}{\frac{v^2}{g} \stackrel{+}{-} r }})
da habe ich einfach die Münze als Scheibe zusätzlich betrachtet und von deren Mittelpunkt den alten Radius des Trichters genommen und durch Winkelbetrachtungen den neuen Radius berechnet
Was habt ihr bei der Zeit bei b) heraus? Ich habe 8 s.
Zuletzt bearbeitet von Limes90 am 15. Nov 2010 16:51, insgesamt 2-mal bearbeitet |
|
 |
Langley
Anmeldungsdatum: 19.10.2010
Beiträge: 12
|
 Langley Verfasst am: 03. Nov 2010 20:45 Titel: Langley Verfasst am: 03. Nov 2010 20:45 Titel: |
 |
|
|
Wie hast du die Zeit bestimmt? Ich bin daran verzweifelt... =/
|
|
 |
eva1
Anmeldungsdatum: 06.10.2010
Beiträge: 532
|
 eva1 Verfasst am: 03. Nov 2010 21:08 Titel: eva1 Verfasst am: 03. Nov 2010 21:08 Titel: |
 |
|
Für die Zeit habe ich 3,4 Sekunden, ist aber ziemlich sicher falsch!
Das mit der Münze ist ziemlich sicher falsch! Denn es steht ja in der Angabe R>>r!
|
|
 |
eva1
Anmeldungsdatum: 06.10.2010
Beiträge: 532
|
 eva1 Verfasst am: 03. Nov 2010 21:08 Titel: eva1 Verfasst am: 03. Nov 2010 21:08 Titel: |
 |
|
|
Wie hast du das mit der Zeit gemacht?
|
|
 |
Limes90
Anmeldungsdatum: 03.11.2010
Beiträge: 39
|
 Limes90 Verfasst am: 03. Nov 2010 23:38 Titel: Limes90 Verfasst am: 03. Nov 2010 23:38 Titel: |
 |
|
bei b) habe ich herausgefunden, dass es eine gleichförmige Bewegung tangential zur Trichterfläche nach unten gibt, ich habe die Funktion z(R) geplottet und dann die Länge der Kurve durch Ausmessen bestimmt, ich wollte zuerst die Bogenlänge bestimmen, doch das Integral war irgendwie nicht lösbar
Warum sollte denn die Funktion mit der Münze total falsch sein? Gut, ich habe den unteren Radius nicht mitbetrachtet.
Ich brauchte r << R für eine Vereinfachung, weil ich eine quadratische Gleichung lösen musste.
Zuletzt bearbeitet von Limes90 am 15. Nov 2010 16:52, insgesamt einmal bearbeitet |
|
 |
eva1
Anmeldungsdatum: 06.10.2010
Beiträge: 532
|
 eva1 Verfasst am: 04. Nov 2010 10:36 Titel: eva1 Verfasst am: 04. Nov 2010 10:36 Titel: |
 |
|
Es gibt sicher keine Leute mehr die Lösungen einschicken!
Abgabetermin war ja der 29.10 und da muss die Lösung bei der Post sein!
Also kann man schon darübe reden!
|
|
 |
FloTor
Anmeldungsdatum: 11.12.2005
Beiträge: 128
|
 FloTor Verfasst am: 04. Nov 2010 12:34 Titel: FloTor Verfasst am: 04. Nov 2010 12:34 Titel: |
 |
|
Wieso bleibt die Masse überhaupt auf einer Höhe? Die wird ja mit einer beliebigen Geschwindigkeit reingepackt... oder meinen die, dass der Vektor senkrecht zur Erdbeschleunigung ist?
Wo kann man denn die Aufgaben einsehen und machen?
|
|
 |
eva1
Anmeldungsdatum: 06.10.2010
Beiträge: 532
|
 eva1 Verfasst am: 04. Nov 2010 14:16 Titel: eva1 Verfasst am: 04. Nov 2010 14:16 Titel: |
 |
|
Einsehen: gar nicht!
Die Masse bleibt auf der Höhe, da sich Normalkraft und Gravitationskraft genau so addieren, sodass sie die benötige Zentripedalkraft ergeben.
Außerdem hängt ja die Trichteform von der Geschwindigkeit ab, wenn du dir die Formel anguckst.
Verstanden?
|
|
 |
FloTor
Anmeldungsdatum: 11.12.2005
Beiträge: 128
|
 FloTor Verfasst am: 04. Nov 2010 15:50 Titel: FloTor Verfasst am: 04. Nov 2010 15:50 Titel: |
 |
|
Ne...
wenn der Vektor der Anfangsgeschwindigkeit zum Beispiel eine kleine z-Komponente hätte, würde der Massepunkt meiner Meinung nach eine Osziallation in z-Richtung ausführen.
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 04. Nov 2010 17:08 Titel: VeryApe Verfasst am: 04. Nov 2010 17:08 Titel: |
 |
|
Mit einer einfachen Skizze kommt man auf


= \frac {g }{ v²} \cdot z + C)
definiert man jetzt den Radius bei z=0 mit runten kommt man auf
= \frac {g}{ v²} \cdot 0 + C )
 )
= \frac {g }{ v²} \cdot z + ln (R_{unten}) )
= e^{\frac {g }{ v²} \cdot z + ln (R_{unten})} )
= e^{\frac {g }{ v²} \cdot z } * R_{unten})
|
|
 |
eva1
Anmeldungsdatum: 06.10.2010
Beiträge: 532
|
 eva1 Verfasst am: 04. Nov 2010 17:52 Titel: eva1 Verfasst am: 04. Nov 2010 17:52 Titel: |
 |
|
| FloTor hat Folgendes geschrieben: | Ne...
wenn der Vektor der Anfangsgeschwindigkeit zum Beispiel eine kleine z-Komponente hätte, würde der Massepunkt meiner Meinung nach eine Osziallation in z-Richtung ausführen. |
Die Anfangsgeschwindigkeit geht nicht in z-Richtung! Das ist gegeben, kannst net wissen. Sie ist horizontal und tangenial zur trichterfläche
|
|
 |
Langley
Anmeldungsdatum: 19.10.2010
Beiträge: 12
|
 Langley Verfasst am: 04. Nov 2010 22:59 Titel: Langley Verfasst am: 04. Nov 2010 22:59 Titel: |
 |
|
Danke VeryApe, denke deine Lösung erreicht volle Punktzahl  . Wie hast du die Sache mit dem Abschätzen der Zeit gemacht? . Wie hast du die Sache mit dem Abschätzen der Zeit gemacht?
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 05. Nov 2010 00:33 Titel: VeryApe Verfasst am: 05. Nov 2010 00:33 Titel: |
 |
|
vielleicht könntest du genauer sagen um welche Zeit es sich handelt.
Den test habe ich nicht gemacht wär auch unfair gewesen  bin doch schon einige Jahre älter bin doch schon einige Jahre älter
|
|
 |
eva1
Anmeldungsdatum: 06.10.2010
Beiträge: 532
|
 eva1 Verfasst am: 05. Nov 2010 10:55 Titel: eva1 Verfasst am: 05. Nov 2010 10:55 Titel: |
 |
|
Ja die Aufgabe mit der Punktmasse fand ich jetzt nicht so schwer. Das müssten, denk ich mal, die meisten geschafft haben. Ich hab es über die Umkehrfunktion gemacht. Es kommt das selbe heraus.
Wie aber geht die Aufgabe, wenn statt der Punktmasse eine Münze hergenommen wird?? Kannst du das vielleicht erklären VeryApe, dann hast auch meinen großen Respekt!
|
|
 |
Limes90
Anmeldungsdatum: 03.11.2010
Beiträge: 39
|
 Limes90 Verfasst am: 05. Nov 2010 13:47 Titel: Limes90 Verfasst am: 05. Nov 2010 13:47 Titel: |
 |
|
Ich habe mal bei der Wettbewerbsleitung nachgefragt, wegen der Diskussion im Internet. Heute bekam ich folgende Antwort:
Hallo xxxxx,
da es leider immer wieder einige Verspätungen bei den Einsendungen gibt (so auch in diesem Jahr), bitte ich Sie, noch bis zum Ende der nächsten Woche mit der Diskussion der Aufgaben im Internet zu warten.
.....
Beste Grüße
Stefan Petersen
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 05. Nov 2010 13:51 Titel: dermarkus Verfasst am: 05. Nov 2010 13:51 Titel: |
 |
|
Danke fürs einholen der Info und fürs Bescheidsagen.
Dann machen wir hier am besten einfach mal vorläufig zu, bis Ende nächster Woche die Runde wirklich für alle vorbei ist.
Die Aufgaben und die Diskussionen dazu sind ja spannend genug, um auch übernächste Woche noch interessant zu sein 
|
|
 |
para
Moderator

Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
 para Verfasst am: 05. Nov 2010 15:12 Titel: para Verfasst am: 05. Nov 2010 15:12 Titel: |
 |
|
Okay. Ich nahm an, dass der Einsendeschluss strikt gehandhabt wird. Aber die Antwort der Wettbewerbsleitung war ja eindeutig. Auch von mir nochmal danke für's Nachfragen, Limes90.
_________________
Formeln mit LaTeX |
|
 |
para
Moderator

Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
 para Verfasst am: 15. Nov 2010 00:01 Titel: para Verfasst am: 15. Nov 2010 00:01 Titel: |
 |
|
Nachdem die erbetene Sperrfrist abgelaufen ist, ist der Thread nun wieder offen. Danke für eure Geduld, und viel Spaß bei der weiteren Diskussion. :)
_________________
Formeln mit LaTeX |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 15. Nov 2010 00:07 Titel: franz Verfasst am: 15. Nov 2010 00:07 Titel: |
 |
|
|
Vielleicht nochmal die Originalaufgabe?
|
|
 |
Limes90
Anmeldungsdatum: 03.11.2010
Beiträge: 39
|
 Limes90 Verfasst am: 15. Nov 2010 17:03 Titel: Limes90 Verfasst am: 15. Nov 2010 17:03 Titel: |
 |
|
Nun wird eine Trichterfunktion vorgegeben:
=R_{oben}/\sqrt{\frac{2g}{v^2} \cdot (h-z) +1})
1. Eine Punktmasse wird mit der tangential und horizontal zur Trichterfläche gerichteten Geschwindigkeit v auf den oberen Rand des Trichters gesetzt. Es soll gezeigt werden, dass deren Höhe sich nicht verändert .
2. Die Punktmasse besitzt nun eine Geschwindigkeit u senkrecht zur Geschwindigkeit v und entlang der Trichterfläche. Die Zeit soll abgeschätzt werden, wann die Masse den Trichter verlässt. Außerdem muss man die Bewegung der Masse beschreiben.
Die erforderlichen Daten für die 2.Aufgabe:
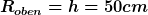 und und 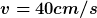 und und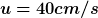
|
|
 |
eva1
Anmeldungsdatum: 06.10.2010
Beiträge: 532
|
 eva1 Verfasst am: 16. Nov 2010 14:08 Titel: eva1 Verfasst am: 16. Nov 2010 14:08 Titel: |
 |
|
|
kommt da jetzt keiner drauf?
|
|
 |
eva1
Anmeldungsdatum: 06.10.2010
Beiträge: 532
|
 eva1 Verfasst am: 19. Nov 2010 16:03 Titel: eva1 Verfasst am: 19. Nov 2010 16:03 Titel: |
 |
|
kommt schon leute! 
|
|
 |
para
Moderator

Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
 para Verfasst am: 21. Nov 2010 13:45 Titel: para Verfasst am: 21. Nov 2010 13:45 Titel: |
 |
|
Für welche Teilaufgabe wird denn jetzt eine Lösung gesucht?
_________________
Formeln mit LaTeX |
|
 |
eva1
Anmeldungsdatum: 06.10.2010
Beiträge: 532
|
 eva1 Verfasst am: 21. Nov 2010 23:18 Titel: eva1 Verfasst am: 21. Nov 2010 23:18 Titel: |
 |
|
Für die hier:
| Limes90 hat Folgendes geschrieben: | Nun wird eine Trichterfunktion vorgegeben:
=R_{oben}/\sqrt{\frac{2g}{v^2} \cdot (h-z) +1})
1. Eine Punktmasse wird mit der tangential und horizontal zur Trichterfläche gerichteten Geschwindigkeit v auf den oberen Rand des Trichters gesetzt. Es soll gezeigt werden, dass deren Höhe sich nicht verändert .
2. Die Punktmasse besitzt nun eine Geschwindigkeit u senkrecht zur Geschwindigkeit v und entlang der Trichterfläche. Die Zeit soll abgeschätzt werden, wann die Masse den Trichter verlässt. Außerdem muss man die Bewegung der Masse beschreiben.
Die erforderlichen Daten für die 2.Aufgabe:
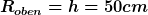 und und 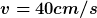 und und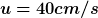 |
|
|
 |
eva1
Anmeldungsdatum: 06.10.2010
Beiträge: 532
|
 eva1 Verfasst am: 23. Nov 2010 17:37 Titel: eva1 Verfasst am: 23. Nov 2010 17:37 Titel: |
 |
|
zu 2.
Limes schrieb per pn, dass es sich um eine gleichförmige Bewegung handelt.
Wie kann man das beweisen/zeigen?
Hat da jemand eine Idee?
|
|
 |
Limes90
Anmeldungsdatum: 03.11.2010
Beiträge: 39
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 23. Nov 2010 22:58 Titel: VeryApe Verfasst am: 23. Nov 2010 22:58 Titel: |
 |
|
ich versteh die Angabe nicht, darum hab ich auch nichts geschrieben.
Ich versteh auch nicht warum das gleichförmig sein soll, wenn die Geschwindigkeit u senkrecht nach unten geht verliert da Ding an potentieller Energie die in kinetischer landet, geschweige denn sollte sie ja in richtung der Ebene gehen sonst hätten wir ja einen stoss.
Ich kapier diesen Teil nicht, aber Respekt an die Leute die das gelöst haben.
Hattet ihr eine Skizze dabei oder war das nur eine Angabe in Text.
|
|
 |
eva1
Anmeldungsdatum: 06.10.2010
Beiträge: 532
|
 eva1 Verfasst am: 23. Nov 2010 23:00 Titel: eva1 Verfasst am: 23. Nov 2010 23:00 Titel: |
 |
|
nur Angabe mit Text!
Was verstehst du denn nicht?
|
|
 |
eva1
Anmeldungsdatum: 06.10.2010
Beiträge: 532
|
 eva1 Verfasst am: 23. Nov 2010 23:11 Titel: eva1 Verfasst am: 23. Nov 2010 23:11 Titel: |
 |
|
Nicht schlecht! Habs verstanden. Genial. Bin Beeindruckt!
Was hast du für e) und f) herausbekommen?
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 23. Nov 2010 23:16 Titel: VeryApe Verfasst am: 23. Nov 2010 23:16 Titel: |
 |
|
v wirkt horizontal tangential, soviel check ich,
in welche Richtung wirkt u.?
parallel in Richtung z Achse, das haut aber mit der Schnittebene nicht hin.
wie wirkt jetzt u genau
|
|
 |
eva1
Anmeldungsdatum: 06.10.2010
Beiträge: 532
|
 eva1 Verfasst am: 24. Nov 2010 14:16 Titel: eva1 Verfasst am: 24. Nov 2010 14:16 Titel: |
 |
|
u geht einfach nach unten !
Also entlang des Trichters nach unten.
|
|
 |
Schätzer
Gast
|
 Schätzer Verfasst am: 24. Nov 2010 18:04 Titel: Schätzer Verfasst am: 24. Nov 2010 18:04 Titel: |
 |
|
|
Ich schätz mal es dauert 2 Sekunden
|
|
 |
eva1
Anmeldungsdatum: 06.10.2010
Beiträge: 532
|
 eva1 Verfasst am: 25. Nov 2010 14:21 Titel: eva1 Verfasst am: 25. Nov 2010 14:21 Titel: |
 |
|
Ich denke Limes90 Lösung ist die Richtige!
Wie wäre es über einen anderen Aufgabenteil zu disskutieren:
Was ist der Unterschied, wenn eine Münze(Radius r Masse m sehr dünn) statt einer Punktmasse im Trichter rotiert?
Dabei: Trichterradius >> Münzradius und die Münze rollt.
|
|
 |
Limes90
Anmeldungsdatum: 03.11.2010
Beiträge: 39
|
 Limes90 Verfasst am: 25. Nov 2010 16:32 Titel: Limes90 Verfasst am: 25. Nov 2010 16:32 Titel: |
 |
|
Hier mal ein Bild von so einem Trichter mit den Geschwindigkeiten u und v. Wie eva1 schon erklärt hat, wird eine Münze mit dem Radius r und der Geschwindigkeit v auf den Trichter gesetzt (ohne u). Diese soll auf der gleichen Höhe bleiben. Es soll der Trichterradius R in Abhängigkeit von z berechnet werden. Dabei ist r << R.
Ich würde mich auch über Lösungen freuen.
| Beschreibung: |
|

Download |
| Dateiname: |
trichter.jpg |
| Dateigröße: |
56.35 KB |
| Heruntergeladen: |
782 mal |
|
|
 |
BbM
Gast
|
 BbM Verfasst am: 25. Nov 2010 17:57 Titel: BbM Verfasst am: 25. Nov 2010 17:57 Titel: |
 |
|
Wenn es nur um das Trägheitsmoment geht,dann ändert sich nichts
Aber natürlich wird die Münze umfallen
|
|
 |
|
















 . Wie hast du die Sache mit dem Abschätzen der Zeit gemacht?
. Wie hast du die Sache mit dem Abschätzen der Zeit gemacht?
