| Autor |
Nachricht |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 22. Sep 2010 15:18 Titel: Kurvenform eines unendlich dünnen Seils Schwerelosigkeit v=v VeryApe Verfasst am: 22. Sep 2010 15:18 Titel: Kurvenform eines unendlich dünnen Seils Schwerelosigkeit v=v |
 |
|
ich eröffne jetzt einen eigenen Thread weil ich mir vorher nicht gedacht hätte das das rauskommen würde. Vielleicht kann das einer kontrollieren und bestätigen oder auch Falsifizieren.
| Beschreibung: |
|

Download |
| Dateiname: |
Differential.jpg |
| Dateigröße: |
29.48 KB |
| Heruntergeladen: |
3199 mal |
Zuletzt bearbeitet von VeryApe am 22. Sep 2010 16:38, insgesamt einmal bearbeitet |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 22. Sep 2010 15:20 Titel: VeryApe Verfasst am: 22. Sep 2010 15:20 Titel: |
 |
|
Dynamisches Gleichgewicht:


}=0=F1_{x} \cdot dy-F1_{y}\cdot dx-dFz_{x} \cdot \frac {dy}{2}-dFz_{y} \cdot \frac {dx}{2} )
!!Biegemomentenfrei!!
Die Terme:

sind unendlich klein zum Quadrat -> in die Mülltone.
daraus folgt:
}=0=F1_{x} \cdot dy-F1_{y}\cdot dx )
*****************************************************
(1) 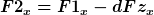
(2) 
(3) 
*****************************************************
y''... Die Steigung der Steigung sprich




=y'' \cdot dx \cdot (F1_{x}-dFz_{x}))

unendlich klein zum Quadrat 

*********************************************************
Grundansatz:


********************************************************


²}=dFz )




rho... Krümmungsradius
mü....Masse pro Meter

^{\frac{3}{2}}}{y''})
^{\frac{3}{2}}})
^{\frac{3}{2}}})
^{\frac{3}{2}}})
************************************************
Grundansatz:

^{\frac{3}{2}}}+\frac {\mu \cdot v² \cdot y'² \cdot y''}{(1+y'²)^{\frac{3}{2}}}=y'' \cdot F1_{x} )
^{\frac{3}{2}}}+\frac { y'² }{(1+y'²)^{\frac{3}{2}}})=F1_{x} )
************************************************
Aus biegemomenten Freiheit folgt:
=\mu \cdot v² \cdot \frac { 1}{\sqrt{1+y'²}})
=\mu \cdot v² \cdot \frac { y'}{\sqrt{1+y'²}})
*************************************************
Aus einer willkürlichen Kurve unter v folgt
das die Zunahme von Fx und von Fy nur durch die Zentrifugalkräfte erfolgt
(1) 
(2) 
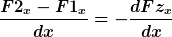

********************************************************
^{\frac{3}{2}}} \rightarrow Fx=\mu \cdot v² \cdot \frac { 1}{\sqrt{1+y'²}})
^{\frac{3}{2}}} \rightarrow Fy=\mu \cdot v² \cdot \frac { y'}{\sqrt{1+y'²}})
Die Gleichheit von Fx und Fy mit F1x und F1y besagt das jede willkürliche Kurve biegemomentfrei unter Zentrifugalbelastung im dynamischen Kräftegleichgewicht sein kann, dabei ist egal ob v=0 oder v=v oder v=unendlich
*********************************************************
Es kommt sogar noch dicker, mit dem hab ich überhaupt nich gerechnet
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 22. Sep 2010 15:45 Titel: VeryApe Verfasst am: 22. Sep 2010 15:45 Titel: |
 |
|
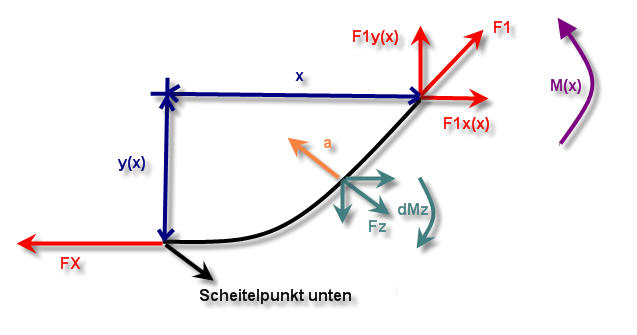
Momentenbilanz - Verifizierung über Geogebra
| Beschreibung: |
|
| Dateigröße: |
23.05 KB |
| Angeschaut: |
6209 mal |
|
Zuletzt bearbeitet von VeryApe am 22. Sep 2010 16:04, insgesamt einmal bearbeitet |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 22. Sep 2010 16:20 Titel: franz Verfasst am: 22. Sep 2010 16:20 Titel: |
 |
|
|
Entschuldigung, aber wie lautet die kurze Frage zur langen Antwort?
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 22. Sep 2010 16:37 Titel: VeryApe Verfasst am: 22. Sep 2010 16:37 Titel: |
 |
|
Mögliche Seilformen egal ob v=0 oder v=v oder v=unendlich.
Wodurch wird dann die Seilform bestimmt?
Ich würde jetzt sagen durch die Krümmung den sie bestimmt das Biegemoment, zwar nicht bei einen uendlich dünnen Seil, aber meistens hat man ja eines das etwas dicker ist hrhr.
Das heißt das Seil wird durch die Krümmung und daraus resultierenden Materialspannung in den Kreiszustand gezwungen sodass die Krümmung gleichbleibt und die Biegemomente im Gleichgewicht sind.
Die Zentrifugalkräfte dürften dabei überhaupt keine Auswirkung haben.
Unter Schwerkraft müßte die Schwerkraft und das Biegemoment die Form des Seils bestimmen.
die Zentrifugalkraft sprich die Geschwindigkeit bestimmt nur wann das Seil durch Normalkräfte reißt, aber meiner Ansicht nach nicht die Form
| Beschreibung: |
|

Download |
| Dateiname: |
Moegliche Seilformen.jpg |
| Dateigröße: |
20.08 KB |
| Heruntergeladen: |
3139 mal |
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 22. Sep 2010 16:41 Titel: VeryApe Verfasst am: 22. Sep 2010 16:41 Titel: |
 |
|
@Franz die Frage ist ob das stimmt.
weil dann die Annahmen zur kurvenform einer hängenden FahrradKette falsch sind. samt deiner Angabe zur dynamischen Version der Kettenlinie.
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 22. Sep 2010 17:41 Titel: schnudl Verfasst am: 22. Sep 2010 17:41 Titel: |
 |
|
VeryApe, deine Gedanken sind wirklich nicht nachzuvollziehen, auch wenn man sich an deine mathematische Schreibweise schon gewöhnt hat. Kann echt sein, dass es Hand und Fuß hat, aber es ist wirklich wirr geschrieben und man findet keinen roten Faden. Vergiss nicht, dass du dich schon tagelang mit dem Thema beschäftigst, andere aber vielleicht nicht.
Kannst du mal versuchen, dich auf das wesentliche zu konzentrieren? Worin unterscheidet sich dein neuer Ansatz zum alten? Und was kommt letztlich raus? Kannst du das ein wenig komprimiert darstellen?
Das soll aber keine inhaltliche Abwertung sein, sondern nur eine Kritik zur Form! Ich schaue es mir trotzdem mal an...bis jetzt sehe ich keinen Unterschied zu früher.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 22. Sep 2010 18:03 Titel: VeryApe Verfasst am: 22. Sep 2010 18:03 Titel: |
 |
|
Tagelang hrhr
Seit gestern abend und heute weil ich frei habe eingehend.
Ich werde da auch keine Zeit mehr reinstecken, für mich ist das beendet.
Es kommt im Endeffekt raus.
Das die Geschwindigkeit des Seils die Form des seils nicht bestimmen kann.
Jede Kurvenform bei egal welcher Geschwindigkeit ist aufgrund Zentrifugalkraft biegefrei.
Die Materialspannungen durch die Krümmung bestimmen die Form des Seils.
Unter Schwerkraft natürlich auch die Schwerkraft.
Das bedeutet für die Fahrradkette das man die Verdrehungen der Kettenglieder berücksichtigen muß und insbesondere die Reibung in den Kettengliedern, ansonsten braucht man gar nicht anfangen.
Und es bedeutet das wir es hier nicht mit einer dynamischen Kettenlinie zu tun haben. sondern mit einer Biegespannung behafteten Linie unter schwerkraft.
Deswegen sind die Ansätze dort falsch.
MFG
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 22. Sep 2010 18:12 Titel: schnudl Verfasst am: 22. Sep 2010 18:12 Titel: |
 |
|
Soll ich das Thema löschen wenn es für dich ohnehin beendet ist?
Du wirst das nicht wollen, da du ja viel Aufwand hineingesteckt hast. Nun soll man bestätigen, was du gemacht hast. Dann wäre es aber gut, zu verstehen, was denn eigentlich die Inputs, der Unterschied zu deinen vorigen Ansätzen und vor allem der Output ist? Welche Formel beschreibt denn nun die Kurvenform? Die war ja schließlich gefragt- oder? Gib uns eine kleine Lesehilfe für deine Ausführungen. Wenn du es nicht machen willst, sei bitte nicht traurig, dass es niemand anschauen mag. Insofern gebe ich franz 100% Recht mit seiner etwas sarkastischen Frage...
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 22. Sep 2010 18:46 Titel: VeryApe Verfasst am: 22. Sep 2010 18:46 Titel: |
 |
|
Bitte nicht lass das noch für Isi.
Er glaubt er hätte eine dynamische Kettenlinie. Muß die Verdrehungen der Kettenlinie nicht berücksichtigen und die Reibung.
Ohne das braucht er aber gar nicht zu starten.
Die Kernaussagen:
Kein Schwerkraftterm, schwerelosigkeit, nur zentrifugalkräfte auf die einzelnen Elemente.
Die Summe der Zentrifugalkräfte einer beliebigen Kurve
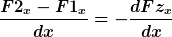

^{\frac{3}{2}}} \rightarrow Fx=\mu \cdot v² \cdot \frac { 1}{\sqrt{1+y'²}})
^{\frac{3}{2}}} \rightarrow Fy=\mu \cdot v² \cdot \frac { y'}{\sqrt{1+y'²}})
********************************************************
Aus dem Dynamischen Gleichgewicht ansatz zur Kettenlinie. Die kettenlinie ist biegemomentfrei folgt das.
=\mu \cdot v² \cdot \frac { 1}{\sqrt{1+y'²}})
=\mu \cdot v² \cdot \frac { y'}{\sqrt{1+y'²}})
Aus Fx(x)=F1(x) und Fy(x)=F1y(x) folgt
Jede Kurve erfüllt die Biegefreiheit.
es gibt keinen Grund warum die Zentrifugalkraft dem Seil eine gewisse Kurvenform aufzwingen soll.
|
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
 isi1 Verfasst am: 22. Sep 2010 18:50 Titel: isi1 Verfasst am: 22. Sep 2010 18:50 Titel: |
 |
|
Ohne dass ich das wirklich im Griff habe, scheint es mir so, als ob VeryApe die Bedingung, F1y/F1x = y', die eigentlich eine Voraussetzung für flexible Seile ist, als Ergebnis gefunden hat. Wie die Humanisten sagen: ὕστερον πρότερον. 
Aber wirklich 'beweisen' kann ich es nicht. Dazu müsste ich erst meine Kette berechnen können.
Habe schon überlegt, den Prof. Werner Maurer direkt anzuschreiben. Kann ja sein, dass man mit Impulsströmen das Problem einfacher formulieren kann.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 22. Sep 2010 19:12 Titel: VeryApe Verfasst am: 22. Sep 2010 19:12 Titel: |
 |
|
Isi deine angesprochene Gleichung für flexible seile ergibt sich aus dem Differential das die Momente der Kraftkomponenten null sein müssen im differential wenn das nicht der fall wäre würde ja ein Biegemoment wirken und es wäre keine Kettenlinie.
Gerade aber in deinem Fall mußt du mit Biegemomenten rechnen die sich bei dir in Verdrehung und in den Reibungsmomenten äußern.
|
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
 isi1 Verfasst am: 22. Sep 2010 20:03 Titel: isi1 Verfasst am: 22. Sep 2010 20:03 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: | Isi deine angesprochene Gleichung für flexible Seile ergibt sich aus dem Differential das die Momente der Kraftkomponenten null sein müssen im Differential wenn das nicht der Fall wäre würde ja ein Biegemoment wirken und es wäre keine Kettenlinie.
Gerade aber in deinem Fall musst du mit Biegemomenten rechnen die sich bei dir in Verdrehung und in den Reibungsmomenten äußern. |
Ja, VeryApe, schon klar, habe ich verstanden. Du hast es ja mustergültig erklärt.
Ich schreibe mir gerade Deine Gleichungen nochmal zusammen, denn ich glaube schon, dass das der richtige Weg ist. Kann natürlich sein, dass es ohne Reibung nicht zum richtigen Ergebnis führt - aber vorläufig würde ich reibungsfrei rechnen.
Mit den Impulsströmen kann man das vielleicht einfacher formulieren, die DGL wird wohl nicht einfacher werden.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 22. Sep 2010 20:18 Titel: VeryApe Verfasst am: 22. Sep 2010 20:18 Titel: |
 |
|
Meine Gleichungen bringen dir aber nichts wenn das oben aufgezeigte richtig ist du mußt sie neuaufsetzen.
Aus folgenden Grund wenn du den untersten Scheitelpunkt hernimmst und wir dort die Kraft FX nennen. dann resultiert dieses FX aus mü * v² und einen konstanten Anteil an Schwerkraft. wenn wir jetzt zum rechten vertikalen scheitel wandern. dann dreht sich dieses mü v² aufgrund der wirkenden Zentrifugalkräfte in die senkrechte Richtung. das heißt Fx aufgrund von zentrifugal wird null Fy wird zu mü* v² und zwar egal welche Kurve bei jeder Kurve ist das so .
Das passt zwar. jedoch bleibt die Schwerkraftkomponente konstant über die Kurve erhalten wie du ja schon in der Kettenlinie gesehen hast. Die bekommst du also im vertikalen rechten Scheitelpunkt nicht weg.
Jede Kurve liefert das selbe Dilemma.
Das bedeutet das bei dieser hängenden Fahrradkette nie und nimmer gültig sein kann.
F1x/F1y=y' ... und das bedeutet wiederum das Biegemomente wirken.
Deswegen hast du bei meiner Differentialgleichung auch wieder die Kettenlinie erhalten und keine 90 Grad tangente. weil sie nie Biegemomentefrei möglich ist.
Ob jetzt nur Verdrehungen zum Ziel führen keine Ahnung.
Vielleicht hilft auch ein Seil das du unter Biegemomente betrachtest.
Die Schwerkraftmomente müssen sich mit dem Biegemoment aufheben das aus der Krümmung des Materials entsteht.
Aufjedenfall ist das ein Haufen Arbeit.
Wünsche noch viel Spass MFG 
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 23. Sep 2010 00:28 Titel: schnudl Verfasst am: 23. Sep 2010 00:28 Titel: |
 |
|
das Ergebnis von VeryApe für die schwerelose Kette ist für mich 100% nachvollziehbar und trotzdem ziemlich verblüffend...ich hätte schwören können das nur ein Kreis stabil wäre. Irgendeinen Fehler sehe ich nicht.
Ich muss das Ergebnis erst mal verdauen... 
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 23. Sep 2010 02:18 Titel: schnudl Verfasst am: 23. Sep 2010 02:18 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: |
Aus folgenden Grund wenn du den untersten Scheitelpunkt hernimmst und wir dort die Kraft FX nennen. dann resultiert dieses FX aus mü * v² und einen konstanten Anteil an Schwerkraft. wenn wir jetzt zum rechten vertikalen scheitel wandern. dann dreht sich dieses mü v² aufgrund der wirkenden Zentrifugalkräfte in die senkrechte Richtung. das heißt Fx aufgrund von zentrifugal wird null Fy wird zu mü* v² und zwar egal welche Kurve bei jeder Kurve ist das so .
Das passt zwar. jedoch bleibt die Schwerkraftkomponente konstant über die Kurve erhalten wie du ja schon in der Kettenlinie gesehen hast. Die bekommst du also im vertikalen rechten Scheitelpunkt nicht weg.
Jede Kurve liefert das selbe Dilemma. |
Da schliesse ich mich nicht an. Wenn man die Kräftebilanzen um die Schwerkraft erweitert, landet man bei der modifizierten "Grundgleichung" (sollte klar sein wie man drauf kommt):
^{1/2}} + \mu g \frac{(1+y'^2)^{1/2}}{y''})
Das Fx bleibt also grundsätzlich einmal nicht erhalten, wie es bei der Kettenlinie der Fall ist. Weshalb sollte es so sein?
Der Anteil der Schwerkraft (2. Term) verschwindet aber am rechten Scheitelpunkt S, wenn dort der Krümmungsradius R endlich ist:
 = \mu g \lim_{x \rightarrow S} \frac{(1+y'^2)^{1/2}}{\kappa (1+y'^2)^{3/2}}= \lim_{x \rightarrow S} R/y' = 0)
Bei der normalen Kettenlinie ist der Grenzwert endlich, da der Krümmungsradius für diesen Limes proportional zu y' und somit unendlich ist: das ist genau die Differenzialgleichung für die Kettenlinie. Wenn man die Voraussetzung Fx=const fallen lässt, braucht man eben eine Krümmung am Scheitelpunkt S. Das ist aufgrund der Geometrie mit dem Zahnrad aber sowieso gegeben.
Es ist spät... 
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 23. Sep 2010 10:11 Titel: VeryApe Verfasst am: 23. Sep 2010 10:11 Titel: |
 |
|
ich kann dir jetzt auf 2 Arten erklären warum ich glaube das ich Recht habe auf eine mechanische Art und auf eine mathematische.
Ich nehme zunächst die mechanische und dann die mathematische.
Vorweg gesagt, ich arbeite immer mit einen dynamisches Gleichgewicht mit den Dalembertschen Trägheitskräften. Ich kann jeden Drehpunkt wählen wenn Summe aller F=0 gültig sein soll.
Wir wissen das jede Kurve aufgrund von Zentrifugalkraftbelastung biegefrei ist. Das bedeutet das sich das Moment der rechten vertikalen Scheitelkraft bezüglich Scheitel unten mit den Momenten der Zentrifugalkomponenten bezüglich Scheitel unten aufheben. Das gilt natürlich für jeden x wert nicht nur für den rechten Scheitel.
Da ich ein dynamisches Gleichgewicht habe kann ich natürlich sofort jeden anderen Drehpunkt wählen ohne etwas falsch zu betrachten.
Ich wähle den Punkt in dem sich untere Scheitelkraft und rechte Scheitelkraft schneiden. Hier müssen sich natürlich die Zentrifugalmomente selbst aufheben weil auch hier gültig sein muß Summe aller M=0
siehe Skizze
| Beschreibung: |
|

Download |
| Dateiname: |
Kurvenformen ohne Schwerkraft.jpg |
| Dateigröße: |
34.83 KB |
| Heruntergeladen: |
1956 mal |
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 23. Sep 2010 11:16 Titel: VeryApe Verfasst am: 23. Sep 2010 11:16 Titel: |
 |
|
Nun die mathematische:
Die Kettenlinie ohne Geschwindigkeit führt auffolgende Gleichung:
 =\mu g \frac{(1+y'^2)^{1/2}}{y''})
Ich kann jetzt F1x' bilden und weiß das die Steigung null sein muß, denn durch was soll sich F1x verändern es wirken ja keine Kräfte in x.
(u * v)'=u'*v+v'u
^{\frac{1}{2}} \cdot y''^{-1} )
^{\frac{1}{2}})
^{-\frac{1}{2}} \cdot 2y' \cdot y'')


^{-\frac{1}{2}} \cdot 2y' \cdot y'' \cdot y''^{-1} + -y''^{-2} \cdot y''' \cdot (1+y'²)^{\frac{1}{2}} )
****************************
^{\frac{1}{2}}} - \frac {(1+y'²)^{\frac{1}{2}} \cdot y'''}{y''^{2}} )
=\mu \cdot g \cdot [\frac {y'}{(1+y'²)^{\frac{1}{2}}} - \frac {(1+y'²)^{\frac{1}{2}} \cdot y'''}{y''^{2}}] = 0)
daraus folgt die Differentialgleichung:
 \cdot y'''}{y' \cdot y''^{2}})
Die Differentialgleichung der Kettenlinie anders geschrieben.
Diese Gleichung hat isi unter hängender Fahrradkette bereits gelöst und kam auf die Kettenlinie,
wieso hab ich aber diese Gleichung sogar bei Zentrifugalansatz erhalten?
ganz einfach:
^{1/2}} + \mu g \frac{(1+y'^2)^{1/2}}{y''})
einmal differenziert ergibt:
^{\frac{3}{2}}} +\mu \cdot g \cdot [\frac {y'}{(1+y'²)^{\frac{1}{2}}} - \frac {(1+y'²)^{\frac{1}{2}} \cdot y'''}{y''^{2}}])
Wodurch ändert sich aber unser Fx nur natürlich nur durch die Zentrifugalkräfte in x.
zur Erinnerung.
^{\frac{3}{2}}} )
aus unseren dynamischen Gleichgewicht heißt das siehe zurück:



sprich
^{\frac{3}{2}}} )
daher muß gültig sein:
^{\frac{3}{2}}} +\mu \cdot g \cdot [\frac {y'}{(1+y'²)^{\frac{1}{2}}} - \frac {(1+y'²)^{\frac{1}{2}} \cdot y'''}{y''^{2}}] =-\frac {\mu \cdot v² \cdot y' \cdot y''}{(1+y'²)^{\frac{3}{2}}} )
es folgt:
^{\frac{1}{2}}} - \frac {(1+y'²)^{\frac{1}{2}} \cdot y'''}{y''^{2}}] =0 )
 \cdot y'''}{y' \cdot y''^{2}})
somit erhalten wir diesselbe Lösung wie bei der statischen Kettenlinie
Die Geschwindigkeit hat einfach keine Auswirkung. es gibt keinen grund für die Zentrifugalkraft das Seil aus der Kettenlinie zu zwingen.
Es gibt keine 90 Grad tangente.
Es treten Biegemomente auf die das Seil in eine Kurve zwingen
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 23. Sep 2010 19:16 Titel: schnudl Verfasst am: 23. Sep 2010 19:16 Titel: |
 |
|
Ich wollte eigentlich nur zeigen, dass Fx nicht konstant ist (für die Schwerkraftkomponente stimmt es aber im Nachhinein betrachtet...) - und das ist es ja auch nicht, da du ja selbst Fx'=-dFz/dx angibst. Aber nun verblüfft mich zugegebenermaßen schon, dass nach dem Differenzieren beide v-Terme rausfallen und die Kettenlinie überbleibt. Das war mir nicht bewusst und ich staune, wie man Opfer falscher Überlegungen werden kann.
Rein gefühlsmässig kann ich es immer noch nicht glauben, aber die Rechnung ist wasserdicht.
Nun verstehe ich auch, wo euer Problem liegt: Die Kette hängt dann einfach so nach unten wie eine nicht bewegte...und dafür gibt es ja eine (überraschend einfache) Lösung. Nur ist das mit der Aufhängung nicht vereinbar...Hmmm

_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 23. Sep 2010 19:22 Titel: VeryApe Verfasst am: 23. Sep 2010 19:22 Titel: |
 |
|
weil die Kette in sich geschlossen ist, also haben wir einen Scheitel, das geht aber nur mit Verdrehungen. wer soll FX Schwer aufheben das übrigens auch noch von oberen in rechten Scheitel dazukommt.
wer soll FX Schwer*2 aufheben. dazu bräuchte man eine Kraft von aussen. oder eben Biegemomente
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 23. Sep 2010 19:42 Titel: schnudl Verfasst am: 23. Sep 2010 19:42 Titel: |
 |
|
naja, das ist jetzt ein technisches Detail, aber die eigentliche Überraschung liegt ja woanders. Wer hätte das gedacht? 
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 23. Sep 2010 19:46 Titel: VeryApe Verfasst am: 23. Sep 2010 19:46 Titel: |
 |
|
Zunächst mal danke das du das durchgeschaut hast,  war auch ziemlich überrascht weil ich mir nicht erklären konnte warum isi die Kettenlinie rausbekommt. war auch ziemlich überrascht weil ich mir nicht erklären konnte warum isi die Kettenlinie rausbekommt.
Fand das interessant um es in einen eigenen Thread zu geben.
Übrigens glaubst du das durch die Verdrehungen die Geschwindigkeit doch einen Einfluss auf die Kette haben kann.
Zwar nicht auf ein Seil sonder halt auf eine Kette.
Je schneller die Kette umso schneller müssen sich die Kettenteile drehen umso größer die Momente. umso weniger muß gültig sein Fy/Fx=y'.
Kann sein das die Geschwindigkeit doch die Kurvenform bestimmt durch Verdrehungen bei einer Kette.
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 23. Sep 2010 20:28 Titel: schnudl Verfasst am: 23. Sep 2010 20:28 Titel: |
 |
|
Im Nachhinein sooo einfach...
Ich habe mich selbst (beim letzten Thread) bei der Umformung Fx=... total verrannt und schrieb dutzende (!) A4 Seiten mit Ausdrücken voll (ich habe die Zettel bis ca. Nr 20 durchnummeriert...du brauchtest dafür 3 Zeilen) , bis ich dann schliesslich das Handtuch warf, und meinte, es sei Zeitverschwendung, da ich die entstehende DG sowieso nicht lösen könne. Kaum fasst man aber zwei Terme bloß geeignet zusammen, wird es plötzlich ur-einfach !
Das hast du gut gemacht ! 
Leider weiß ich nicht, was du mit den Verdrehungen meinst. Ich muss auch gestehen, dass mein Wissensdrang für dieses Thema nun erst mal gestillt ist - ich beisse immer noch geistig am Ergebnis und habe noch keinen Kopf für die Details der Aufhängung...
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 23. Sep 2010 20:42 Titel: VeryApe Verfasst am: 23. Sep 2010 20:42 Titel: |
 |
|
das zusammenfassen war der Verdienst von isi. der hat das gleich gesehen. hab selber mit langen Termen herumgerechnet. Nachzusehen auf kurvenform einer Dynamischen Fahrradkette.
Mit Verdrehungen mein ich das die Kettenglieder ja mit einer Art zwei gelenkstäben drehend verbunden sind und sich die ganze Zeit verdrehen. Wenn dieser in unterschiedliche Krümmungen laufen werden sie drehend entweder verzögert oder beschleunigt je nach Krümmung. dazu müssen Momente wirken, die das ganze in Drehungen bringen, je schneller sich die Kette bewegt ob so stärker verzögern oder beschleunigen müssen diese bei Krümmungsänderung.
Aber das soll Isi herausfinden,
Isi wenn du dazu mal ne Lösung hast poste sie mal würd mich interessieren.
Ich hab nun auch genug von den Thema und bedanke mich nochmal bei schnudel für die Hilfe, der hat sich eigentlich immer Zeit genommen sogar als ich gedacht hatte ich hätte einen Fehler in der klassischen Mechanik entdeckt lol  verdammtes Buch. verdammtes Buch.
|
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
 isi1 Verfasst am: 23. Sep 2010 21:22 Titel: isi1 Verfasst am: 23. Sep 2010 21:22 Titel: |
 |
|
Eine andere Möglichkeit, VeryApe,
die Kettenlinie zu berechnen, ist die Variationsrechnung.
Dieser Ansatz zeigt recht verständlich, dass Deine Überlegungen richtig sind.
Kettenlinie: Man sucht eine Kurve fester Länge zwischen A und B , für die der Schwerpunkt der Kette am tiefsten liegt. Man kann auch sagen, für die die Energie W=∫y(x)*g*dm minimal wird. Natürlich kommt auch der cosh raus.
mit Geschwindigkeit v: In unserem Fall wird zu W noch die kin. Energie ∫v²/2*dm addiert.
Wie man immer die Kurve legt, bleibt dieser Term konstant, da v und ∫dm konstant sind, und beeinflusst das Ergebnis nicht.
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 24. Sep 2010 13:10 Titel: schnudl Verfasst am: 24. Sep 2010 13:10 Titel: |
 |
|
Diesen Variations-Ansatz habe ich anfangs verworfen, weil er keine Abhängigkeit von v aufzeigte.
Damals war ich noch felsenfest überzeugt, dass dies nicht sein könne, und vermutete daher, dass der Lagrange Formalismus hier aus irgendeinem Grund nicht anwendbar sei. Stattdessen versuchte ich, ein Variationsprinzip zu finden, welches die Zentrifugalkräfte mit einbezieht...

Sicher bin ich mir aber immer noch nicht ganz. In den mir bekannten Herleitungen des Lagrange Formalismus wird von holonomen Zwangsbedingungen ausgegangen. Diese hier scheinen nicht in diese Kategorie zu fallen.
Ich habe mir die ganze Zeit ein Ersatzmodell für die Kette zurechtgelegt: Ein flexibles Rohr, in dem Flüssigkeit im Kreis gepumpt wird. Die Wandkräfte die dann auf das Rohr an der Innenseite ausgeübt werden, sind Zwangskräfte und keine von aussen eingeprägten Kräfte. Deshalb glaube ich, dass der Lagrange Mechanismus möglich sein könnte. Beweis habe ich aber keinen...aber ich glaube versuchsweise dran!
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
 isi1 Verfasst am: 24. Sep 2010 19:43 Titel: isi1 Verfasst am: 24. Sep 2010 19:43 Titel: |
 |
|
Ich tendiere eigentlich auch zu Deiner Meinung, schnudl, denn das Lasso zeigt ja, dass es einen sauberen Kreis gibt.
VeryApes Idee, das Seil könnte sich elastisch strecken (Es treten Biegemomente auf die das Seil in eine Kurve zwingen) wird an der Lassoschlaufe widerlegt (Siehe Bild in diesem Thema:
http://forum.physik-lab.de/ftopic6588.html ).
Andererseits hatte ich ja berichtet:
| isi1 hat Folgendes geschrieben: | | VeryApe hat Folgendes geschrieben: | | woher hast du die Aufgabe? |
Von einem Kollegen, der an einem Kettenflaschenzug eine bauchförmige Kurve der Antriebskette beobachtet hat, während die Last das Kettenrad antreibt. Die Kette wird dabei oben nach links herausgeschleudert, der Bauch war nur ca. 1/2 Meter, darunter und rechts hatte die Kette etwa die Form des Ruhezustands - sagt er. |
Die bauchförmige Kurve ließe sich durch 'Herausschleudern' der Kette durch das Zahnrad deuten.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 25. Sep 2010 10:27 Titel: VeryApe Verfasst am: 25. Sep 2010 10:27 Titel: |
 |
|
Isi ich glaube das du hier einen Denkfehler unterliegst.
wenn du ein Seil betrachtest das zwischen zwei Reibungsfreien Umlenkrollen durchhängt. auf der einen Seite befindet sich eine Seiltrommel auf der das Seil aufgewickelt ist auf der anderen Seite ein Motor und du betrachtest das komplett reibungsfrei, dann hängt das Seil bei v=0 in der Kettenlinie durch, wenn du das Seil durch den Motor beschleunigst dann wird sich das Seil natürlich nach oben beschleunigen sprich die länge zwischen den Umlenkrollen die durchhängt wird geringer. es bildet sich nach der Beschleunigung wieder eine Kettenlinie aber eine mit kürzer Länge und die Geschwindigkeit ist größer.
Meine Aussage ist aber das das Seil bei egal welcher Geschwindigkeit genau wieder die gleiche Kettenlinie beschreiben könnte. sprich ich könnte mit einer dritten Umlenkrolle während der Beschleunigung arbeiten die im untersten Scheitelpunkt ansetzt und nach der Seil beschleunigung wieder wegnehmen die gleiche Kettenkurve würde sich konstant halten.
"das heißt die Beschleunigung bestimmt natürlich die Kurve"
Meine Betrachtungen bezogen sich aber darauf ob die Form durch die Geschwindigkeit bestimmt wird und meine Betrachtung bezog sich bei der Schwerkraft auf einen konstanten Punkt von dem die äußere Kraft herrührt.
zum Beispiel der oberste Radaufhängungspunkt.
Der Lassowerfer beschleunigt das Seil ständig, die Haltekraft des Seil varriert ständig,weil er die Hand mit dreht, Sie kommt einmal von oben und einmal von unten oder von der Seite. er bringt durch die Beschleunigungen das Seil in eine Kreisform.
wenn ich eine kurze Schnur zusammenbinde und auf meinen Finger lege. meinen Finger dabei immer auf und abbewege und das ganze leicht ins drehen bringe, wird die Schnur auch einen Kreis beschreiben.
bei betrachtung mit einer konstanten Haltekraft und SChwerkraft herrschen Biegemomente,
aber genauso beim Lassowerfer treten Biegemomente auf sogar nochmer.
Und zwar immer auf der gegenüberliegenden Seite zur der Seite wo er die Haltekraft aufbringt, sind sie am maximalsten.
Nachtrag: die einzelnen Glieder des Seil werden auch bei konstanter Geschwindigkeit des Seil beschleunigt von dem Rede ich aber hier nicht.
Hier geht es um eine Beschleunigung die die Geschwindigkeit der einzelnen Kettenglieder verändert, also um Kräfte die Energie zuführen
|
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
 isi1 Verfasst am: 25. Sep 2010 11:47 Titel: isi1 Verfasst am: 25. Sep 2010 11:47 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: | | Meine Aussage ist aber das das Seil bei egal welcher Geschwindigkeit genau wieder die gleiche Kettenlinie beschreiben könnte. sprich ich könnte mit einer dritten Umlenkrolle während der Beschleunigung arbeiten die im untersten Scheitelpunkt ansetzt und nach der Seil Beschleunigung wieder wegnehmen die gleiche Kettenkurve würde sich konstant halten. |
Da stimmen wir überein, VeryApe,
Deine ausführlichen Berechnungen und auch die Energiebetrachtung zeigen das, wenn auch meine Intuition (soll bei Frauen besonders ausgeprägt sein) dagegen spricht.
Deine Maschine könnte man konkretisieren:
Rechts saugt ein Motor die Kette mit der Geschwindigkeit v ein, links spendet ein zweiter die Kette in genau der Richtung der Kettenlinie.
Das gilt rechts auch beim Zahnrad, links schleudert das Ritzel die Kette heraus, sie wird dann durch ihr Gewicht und den Zug der hängenden Kette nach unten abgelenkt. Der Bauch entsteht vielleicht durch einen stationären Schwingungsvorgang (ähnlich der Welle beim Eisbach)
http://de.wikipedia.org/w/index.php?title=Datei:Eisbach_surfen_1.jpg&filetimestamp=20090806223125
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 25. Sep 2010 22:47 Titel: VeryApe Verfasst am: 25. Sep 2010 22:47 Titel: |
 |
|
Der Bauch entsteht während der Beschleunigung der Kette. eigentlich müsste er sich legen, wäre da nicht die Reibung in den Kettengliedern, der Motor muß ständig die Kette beschleunigen umso konstant auf Geschwindigkeit zu halten.
Ein völlig Flexibles Seil wird bei beschleunigung in einer Richtung eine Linie beschreiben es wird auf einen Strich in Richtung beschleunigung zusammenfallen. Es wird auch nie einen Kreis beschreiben. Wenn du nicht in jeden Massepunkt die Beschleunigung so ausrichtest das es zu einen Kreis wird. Meistens bringt aber seine Kraft zentral in einen Angriffspunkt auf (Lassowerfer) und kann selten agieren wie die Schwerkraft.
wäre das Lasso völlig flexibel würde es ihm zusammenfallen und nie einen Kreis beschreiben.
Meine Argumentation, aber ich bin kein Professor für dynamische Systeme  obs richtig ist kannsd du ja mal herausfinden. obs richtig ist kannsd du ja mal herausfinden.
|
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
 isi1 Verfasst am: 26. Sep 2010 11:46 Titel: isi1 Verfasst am: 26. Sep 2010 11:46 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: | | Der Bauch entsteht während der Beschleunigung der Kette. |
Ja, VeryApe, genau diesen Verdacht hatte ich auch schon.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
|
























 verdammtes Buch.
verdammtes Buch.