| Autor |
Nachricht |
WebFritzi
Anmeldungsdatum: 07.02.2008
Beiträge: 13
|
 WebFritzi Verfasst am: 07. Feb 2008 11:16 Titel: Indefinite Sturm-Liouville-Operatoren in der Anwendung WebFritzi Verfasst am: 07. Feb 2008 11:16 Titel: Indefinite Sturm-Liouville-Operatoren in der Anwendung |
 |
|
Hi!
Ich bin Mathematiker und beschäftige mich zur Zeit mit
indefiniten Sturm-Liouville-Operatoren (alles eindimensional).
Die treten z.B. auf, nachdem man für eine lineare
Transportgleichung (oder Bewegungsgleichung?)
einen Sep-Ansatz gemacht hat.
Nun würde ich gerne wissen, ob ihr noch andere Gebiete
eurer Disziplin kennt, in denen solche Operatoren auftauchen.
Sie haben die Form
' + qf \right).)
Man nennt r die Gewichtsfunktion und p und q die Koeffizienten.
Wichtig ist hier, dass die Gewichtsfunktion r auch negativ werden
kann! |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 07. Feb 2008 12:37 Titel: dermarkus Verfasst am: 07. Feb 2008 12:37 Titel: |
 |
|
Zu den Anwendungsgebieten, in denen Differentialgleichungen vorkommen können, die zu diesem Operator gehören, kann ich bisher erst vage umschreiben, dass man so etwas in der Transporttheorie antreffen wird, also zum Beispiel bei Diffusionsprozessen, und wohl auch bei einer schwingenden Saite, zum Beispiel wenn die Dicke dieser Saite entlang ihrer Länge variiert.
Darf ich mal eine, vielleicht auch dumme, Rückfrage stellen? Wenn ich das richtig verstehe, ist dein 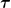 der Operator, und der Operator, und ) , , ) , , ) und und ) alles von der angesprochenen einen betrachteten Raumdimension alles von der angesprochenen einen betrachteten Raumdimension  abhängige Funktionen; und der Strich meint die Ableitung nach diesem abhängige Funktionen; und der Strich meint die Ableitung nach diesem  . Und wenn ich das richtig nachgeschlagen habe, dann sind die Differentialgleichungen, die zu diesem Operator gehören, von der Form . Und wenn ich das richtig nachgeschlagen habe, dann sind die Differentialgleichungen, die zu diesem Operator gehören, von der Form
 - \lambda f(x) = \frac{g(x)}{r(x)})
, die auch so geschrieben werden kann:
 \frac{\dd}{\dd x}f(x) \right) + q(x)f(x) - \lambda r(x) f(x) = g(x) $ } \begin{eqnarray*})
. Dabei halte ich  für eine konstante Zahl größer oder gleich Null und für eine konstante Zahl größer oder gleich Null und ) für eine "beliebige, einigermaßen anständige" (Physikersprache für eine "beliebige, einigermaßen anständige" (Physikersprache  ) von ) von  abhängige Funktion. abhängige Funktion.
Kann man dann nicht immer das ) so wählen, dass das so wählen, dass das ) auf dem gesamten Intervall, das man zu betrachten hat, größer als Null ist? Dumme Frage eines Physikers: Wozu braucht der Mathematiker dann noch eine Betrachtung für Funktionen auf dem gesamten Intervall, das man zu betrachten hat, größer als Null ist? Dumme Frage eines Physikers: Wozu braucht der Mathematiker dann noch eine Betrachtung für Funktionen ) , die kleiner oder gleich Null werden können? , die kleiner oder gleich Null werden können?
Zuletzt bearbeitet von dermarkus am 07. Feb 2008 14:21, insgesamt einmal bearbeitet |
|
 |
WebFritzi
Anmeldungsdatum: 07.02.2008
Beiträge: 13
|
 WebFritzi Verfasst am: 07. Feb 2008 14:21 Titel: WebFritzi Verfasst am: 07. Feb 2008 14:21 Titel: |
 |
|
Uiui, da muss ich wohl ein wenig ausholen. Also, die Differentialgleichungen, die mit diesem Differentialausdruck 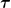 (noch kein Operator!) zusammenhaengen, sind natuerlich die folgenden: (noch kein Operator!) zusammenhaengen, sind natuerlich die folgenden:
f = g.)
Ausgeschrieben ist das
' + qf - \lambda r f = r g.)
Die Sache ist die: Der Mathematiker (und natuerlich auch der Physiker) will einen Hilbertraum, in dem er den Differentialausdruck al Operator betrachten kann. Ist r positiv, dann waehlt er fuer gewoehnlich den mit r gewichteten L^2-Raum ) , der aus den Funktionen besteht, fuer die gilt , der aus den Funktionen besteht, fuer die gilt

Man betrachtet den Differentialausdruck auf dem Unterraum
 : f,pf'\,\text{ sind absolut stetig und }\,\tau f \in L^2_r(a,b)\right\}.)
Der Operator  definiert auf definiert auf  heisst dann der maximale Operator. Diesen kann man um ein paar Dimensionen einschraenken und bekommt dann den minimalen Operator. Dazwischen liegen die selbstadjungierten Realisierungen. heisst dann der maximale Operator. Diesen kann man um ein paar Dimensionen einschraenken und bekommt dann den minimalen Operator. Dazwischen liegen die selbstadjungierten Realisierungen.
Nun, wenn r jetzt aber nicht mehr positiv ist, hat man mit ) keinen Hilbertraum mehr, sondern ein sogenannter Kreinraum. Die Spektraleigenschaften von selbstadjungierten Operatoren in Hilbert- und Kreinraeumen unterscheiden sich allerdings sehr. Ist r also indefinit, verkompliziert sich einiges. keinen Hilbertraum mehr, sondern ein sogenannter Kreinraum. Die Spektraleigenschaften von selbstadjungierten Operatoren in Hilbert- und Kreinraeumen unterscheiden sich allerdings sehr. Ist r also indefinit, verkompliziert sich einiges. |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 07. Feb 2008 15:26 Titel: dermarkus Verfasst am: 07. Feb 2008 15:26 Titel: |
 |
|
OK,
) \cdot r(x) = ( {\rm mein} \, g(x)))
und der Differentialausdruck 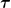 wird erst dann zum Operator, wird erst dann zum Operator,  , wenn man einen zugehörigen Hilbertraum wählen kann. , wenn man einen zugehörigen Hilbertraum wählen kann.
Und ich glaube verstanden zu haben, wenn du von "indefinit" sprichst, meinst du, dass das ) auch negativ werden kann, d.h., dass man nicht von vorneherein sagen kann, ob das auch negativ werden kann, d.h., dass man nicht von vorneherein sagen kann, ob das ) , mit dem man es da zu tun hat, positive oder negative Werte annimmt. , mit dem man es da zu tun hat, positive oder negative Werte annimmt.
------------------------
Mein Frage von oben, etwas konkreter formuliert:
Wenn ich der Frage nachgehe, ob es in der Physik Beispiele für die Anwendung eines solchen Falles gibt, dann schaue ich direkt auf die Differenzialgleichung, die ich aus einem physikalischen Zusammenhang erhalte. Und in dieser Differentialgleichung steht ja zunächst noch kein ) , kein , kein  und kein und kein ) drin, sondern nur die Funktion drin, sondern nur die Funktion ) mit mit  = q(x) - \lambda \cdot r(x)) . .
Nun gehe ich her und wähle mir eine Funktion ) , so, dass sie im gesamten betrachteten Intervall positiv ist und zusätzlich dafür sorgt, dass das Integral , so, dass sie im gesamten betrachteten Intervall positiv ist und zusätzlich dafür sorgt, dass das Integral |^2 r(x) \, \dd x $ \begin{eqnarray*}) im betrachteten Intervall endlich wird. Aus dieser Festlegung des im betrachteten Intervall endlich wird. Aus dieser Festlegung des ) bekomme ich dann mein bekomme ich dann mein  = h(x) + \lambda \cdot r(x) $ \begin{eqnarray*}) . .
Gibst du mir recht, dass man mit dieser Vorgehensweise jedes physikalische Problem, das die Form dieser Differentialgleichung annimmt, lösen kann, ohne dass man sich mit der Möglichkeit eines negativ werdenden ) beschäftigen muss? beschäftigen muss?
Oder gibt es vielleicht zusätzliche Bedingungen für ) , ,  und/oder und/oder ) , die dem entgegensprechen? , die dem entgegensprechen? |
|
 |
WebFritzi
Anmeldungsdatum: 07.02.2008
Beiträge: 13
|
 WebFritzi Verfasst am: 07. Feb 2008 15:41 Titel: WebFritzi Verfasst am: 07. Feb 2008 15:41 Titel: |
 |
|
Ich verstehe nicht ganz, worauf du hinaus willst. Wir Mathematiker gehen direkt von dem gegebenen Differentialausdruck aus. Wir nehmen dabei an, die Funktionen r,p,q seien gegeben. Dann versuchen wir, die Spektra der sogenannten selbstadjungierten Realisierungen zu bestimmen.
Was du da machst, verstehe ich nicht. Irgendwie gehst du gar nicht von einem gegebenen r aus. Kann es nicht sein, dass man einen physikalischen Vorgang hat, der sich mit Hilfe eines obigen Differentialausdrucks beschrieben laesst, wobei die Funktionen r,p,q fest gegeben sind? Da kann man dann nichts mehr angleichen, sondern muss damit arbeiten. Ob man will oder nicht.
Ach so, ich hatte noch eines vergessen. p muss positiv sein. Der Einfachheit halber koennen wir auch p = 1 waehlen, also
.)
Es waere schoen, wenn du mir deinen letzten Beitrag nochmal etwas genauer erklaeren koenntest. |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 07. Feb 2008 16:24 Titel: dermarkus Verfasst am: 07. Feb 2008 16:24 Titel: |
 |
|
Ich schreibs mal mit deiner Definition von ) hin: hin:
 \frac{\dd}{\dd x}f(x) \right) + q(x)f(x) - \lambda r(x) f(x) = g(x)\cdot r(x) )
Hier kann ich ja einfach ausklammern und erhalte:
 \frac{\dd}{\dd x}f(x) \right) + \underbrace{\left(q(x) - \lambda r(x)\right)}_{=h(x)} f(x) = g(x)\cdot r(x) )
Was ich beim Aufstellen der Differentialgleichung aus der Physik erhalte, ist ja nur das ) . .
Das Aufspalten von ) in in ) und und ) kann ich dann beliebig machen, nämlich so, dass sich das mathematisch am einfachsten lösen lässt. kann ich dann beliebig machen, nämlich so, dass sich das mathematisch am einfachsten lösen lässt. |
|
 |
WebFritzi
Anmeldungsdatum: 07.02.2008
Beiträge: 13
|
 WebFritzi Verfasst am: 07. Feb 2008 16:28 Titel: WebFritzi Verfasst am: 07. Feb 2008 16:28 Titel: |
 |
|
| dermarkus hat Folgendes geschrieben: |
Was ich beim Aufstellen der Differentialgleichung aus der Physik erhalte, ist ja nur das ) . .
|
Meiner Meinung nach nicht. Du hast das q. Das h entsteht doch dadurch, dass du Lambda als Eigenwertparameter einfuehrst. Ich denke da an sowas wie die Quantentheorie, wo man halt seine Differentialoperatoren hat und nach den stabilen Zustaenden sucht (d.h. Eigenwerte bzw. Eigenfunktionen). |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 07. Feb 2008 17:27 Titel: dermarkus Verfasst am: 07. Feb 2008 17:27 Titel: |
 |
|
Ah, danke, jetzt hab ichs endlich kapiert 
Das Lambda ist natürlich nicht, wie ich oben geschrieben hatte, einfach nur irgendeine konstante Zahl, sondern folgt natürlich direkt aus dem Separationsansatz als Separationskonstante (=Eigenwertparameter).
Damit sind natürlich auch ) und und ) festgelegt und nicht mehr frei wählbar, und meine Frage von oben war tatsächlich nicht besonders helle festgelegt und nicht mehr frei wählbar, und meine Frage von oben war tatsächlich nicht besonders helle 
------------------------------------------------------------------
Dafür kann ich jetzt schon ein bisschen konkreter sagen, wo so etwas in der Physik vorkommt:
Bei Diffusionsvorgängen in Form der Diffusionsgleichung
 - \frac{1}{D} \frac{\partial }{\partial t} \varrho(x,t) =0)
mit der Teilchenkonzentration ) und der Diffusionskonstanten und der Diffusionskonstanten 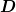 . .
Bei Schwingungsvorgängen in Form der Wellengleichung
 - \frac{\partial^2}{\partial t^2} u(x,t) =0)
mit der Wellenausbreitungsgeschwindigkeit  und der Auslenkung der Welle und der Auslenkung der Welle ) . .
Je nach Anfangs- und Randbedingungen sowie Eigenschaften des Systems (zum Beispiel eine ortsabhängige Diffusionskonstante oder eine ortsabhängige Schallgeschwindigkeit c(x) in einer Saite, deren Dicke sich mit dem Ort x verändert) bekommt man damit auch kompliziertere Fälle als in einfachen Beispielen wie
hier und im Beispiel hier
Ob man damit allerdings sogar einen Fall mit negativ werdendem ) konstruieren kann, habe ich bisher noch nicht eruiert. konstruieren kann, habe ich bisher noch nicht eruiert. |
|
 |
WebFritzi
Anmeldungsdatum: 07.02.2008
Beiträge: 13
|
 WebFritzi Verfasst am: 07. Feb 2008 18:52 Titel: WebFritzi Verfasst am: 07. Feb 2008 18:52 Titel: |
 |
|
Vielen Dank fuer deine Ausfuehrungen.
| dermarkus hat Folgendes geschrieben: |
Ob man damit allerdings sogar einen Fall mit negativ werdendem ) konstruieren kann, habe ich bisher noch nicht eruiert. konstruieren kann, habe ich bisher noch nicht eruiert.
|
Und genau darum geht's.  |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 07. Feb 2008 19:23 Titel: dermarkus Verfasst am: 07. Feb 2008 19:23 Titel: |
 |
|
Ist folgender Fall schon interessant und brauchbar für deine Zwecke?
Saite mit ortsabhängiger Wellenausbreitungsgeschwindigkeit wie oben. (Zum Beispiel =c_0+\frac{c_0}{10}\frac{x}{\ell} $ \begin{eqnarray*}) für für  .) Das Quadrat der Geschwindigkeit ist allein schon wegen des Quadrates garantiert immer größer oder gleich Null, hier gilt .) Das Quadrat der Geschwindigkeit ist allein schon wegen des Quadrates garantiert immer größer oder gleich Null, hier gilt
 > 0) . .
Aus der Wellengleichung

und dem Separationsansatz  \cdot T(t)) folgt folgt

und damit
} X =0)
mit = - \frac{1}{c^2(x)} < 0) sowie sowie  , ,  und und  . .
---------------------------------------
Als Randbedingungen könnte man =X (x=\ell)=0) nehmen, das wäre die an beiden Enden eingespannte Saite. Als physikalisch sinnvolle Lösung würde ich eine Überlagerung von stehenden Wellen erwarten, die zwar ortsabhängig eine veränderliche Wellenlänge und Ausbreitungsgeschwindigkeit haben, aber deren Umlaufzeiten für einmal hin- und herlaufen das Inverse ihrer Schwingungsfrequenzen sind. nehmen, das wäre die an beiden Enden eingespannte Saite. Als physikalisch sinnvolle Lösung würde ich eine Überlagerung von stehenden Wellen erwarten, die zwar ortsabhängig eine veränderliche Wellenlänge und Ausbreitungsgeschwindigkeit haben, aber deren Umlaufzeiten für einmal hin- und herlaufen das Inverse ihrer Schwingungsfrequenzen sind. |
|
 |
WebFritzi
Anmeldungsdatum: 07.02.2008
Beiträge: 13
|
 WebFritzi Verfasst am: 08. Feb 2008 16:52 Titel: WebFritzi Verfasst am: 08. Feb 2008 16:52 Titel: |
 |
|
Hallo Markus,
nein, sorry. Das ist nicht wirklich interessant, da r < 0. Interessant wird es, wenn r das Vorzeichen wechselt. Und RICHTIG interessant wird es, wenn der Differentialoperator auf ganz IR betrachtet wird.
Aber ich danke dir, dass du dir die Muehe machst und die Zeit nimmst!  |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 09. Feb 2008 01:56 Titel: dermarkus Verfasst am: 09. Feb 2008 01:56 Titel: |
 |
|
Meinst du da Funktionen r(x) mit Unstetigkeitsstelle beim Wechsel zwischen positiven und negativen Werten, oder darf r(x) auch Nullstellen haben, um stetig zwischen plus und minus zu wechseln?
----------------------------------
Jedenfalls scheinen da wohl etwas wildere Situationen nötig sein als einfache Diffusionsvorgänge oder schwingende Saiten.
Bisher habe ich die Vermutung, dass man da vielleicht im Zusammenhang mit Diffusion in Festkörpern suchen könnte, wo der Diffusionskoeffizient eventuell, vielleicht irgendwie im Zusammenhang mit negativ werdenden effektiven Massen, negativ werden könnte.
Und eine schon etwas konkretere Vermutung, dass zum Beispiel bei Diffusion von geladenen Teilchen in Flüssigkeiten in porösen Materialien Diffusionskonstanten ziemlich variabel werden können, und dabei auch negative Werte annehmen können; siehe zum Beispiel
http://ciks.cbt.nist.gov/~garbocz/FFvDiff/FFvDiff/index.html |
|
 |
WebFritzi
Anmeldungsdatum: 07.02.2008
Beiträge: 13
|
 WebFritzi Verfasst am: 10. Feb 2008 03:28 Titel: WebFritzi Verfasst am: 10. Feb 2008 03:28 Titel: |
 |
|
Hi Markus,
| dermarkus hat Folgendes geschrieben: |
Meinst du da Funktionen r(x) mit Unstetigkeitsstelle beim Wechsel zwischen positiven und negativen Werten, oder darf r(x) auch Nullstellen haben, um stetig zwischen plus und minus zu wechseln?
|
Das ist ziemlich egal. Im allgemeinen setzen wir stets voraus, dass r lokal integrierbar ist (also über jedes kompakte Intervall) und fast überall ungleich Null. Also kann r eine recht "wilde" Funktion sein. |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 14. Feb 2008 13:56 Titel: dermarkus Verfasst am: 14. Feb 2008 13:56 Titel: |
 |
|
Weitere Situationen, in denen der Diffusionskoeffizient negativ werden und damit sein Vorzeichen wechseln kann, sind
* turbulente Strömungen mit Diffusion
Phys. Rev. E 61, 1390
( Link zum Paper bei Physical Review E online )
* turbulente/chaotische Strömungen mit Diffusion und chemischen Reaktionen
http://eprints.nottingham.ac.uk/498/1/vikhanskycox.pdf
* Diffusion in Medien mit Temperaturgradienten
J. Chem. Phys. 121, 3874
( Link zum Paper bei Journal of Chemical Physics online)
Wenn du die Absicht hast, für die Vorgehensweise beim Lösen deiner Differentialgleichungen reale physikalische Modelle zum Vergleich und zur Inspiration heranzuziehen, dann dürfte es sich also für dich lohnen, die physikalischen Mechanismen, die in solchen Beispielen wirksam sind, genauer unter die Lupe zu nehmen, und die Bedingungen und Situationen zu betrachten, unter und in denen die räumliche und zeitliche Abhängigkeit der Parameter in diesen Versuchen separabel oder in guter Näherung separabel sind.
Wenn du hingegen einfach nur ein paar mögliche Anwendungen dieser Mathematik für den Outlook eines Papers brauchst, dann reicht dir wohl auch schon eine etwas allgemeinere Sichtweise auf diese physikalischen Anwendungen.
Helfen dir die bisherigen Anstöße schon etwas weiter? Ein guter Suchtipp fürs Googeln in diesem Zusammenhang dürfte übrigens eine Suche nach
"negative diffusion coefficient"
"diffusion coefficient" "changes sign"
und ähnlichem sein, mit solchen Methoden habe ich die konkreten Papers und Links ausgegraben, die ich dir nennen konnte. |
|
 |
WebFritzi
Anmeldungsdatum: 07.02.2008
Beiträge: 13
|
 WebFritzi Verfasst am: 14. Feb 2008 14:23 Titel: WebFritzi Verfasst am: 14. Feb 2008 14:23 Titel: |
 |
|
WOW, danke, Markus. Da werde ich mal bei Gelegenheit reinschauen.
Das Problem ist das folgende: Wir in der reinen Mathematik muessen
immer mehr herausstellen, wie unsere Ergebnisse angewandt werden
koennen. Das moegen die Financiers. Ich find's zwar bescheuert, aber
so ist es nunmal. Wenn deine Beispiele wirklich passen sollten, waere
das phaenomenal!  |
|
 |
|
|
















 ) von
) von 
