Gekoppelte Schwingung

PILOM · Anmeldungsdatum: 11.12.2022 Beiträge: 8

Meine Frage:
Ich habe ein Problem bei folgender Aufgabe:
Ein ebenes mathematisches Pendel (Länge L) mit Masse m ist im homogenen Schwerefeld der Erde an einer Masse M aufgehängt und schwingt in der x-y?Ebene. Die Bewegung der Masse M, die durch eine Feder (Federkonstante k) mit der Wand verbunden ist, sei auf die x-Achse beschränkt.
a) Wählen Sie geeignete generalisierte Koordinaten und bestimmen Sie die Lagrange-Funktion.
b) Bestimmen Sie die Bewegungsgleichungen mithilfe der Lagrange-Gleichungen zweiter Art.
c) Bestimmen Sie die Eigenschwingungen des Systems unter der Annahme kleiner Auslenkung p <<1 mit k = 4mg/L und M = 3m.
Die a) und b) konnte ich lösen, aber bei der c) habe ich Probleme

Meine Ideen:
Ich habe als Koordinaten die Auslenkung der Masse M und den Winkel p gewählt. Damit komme ich dann nach anwenden der Angaben von c) auf die Bewegungsgleichungen:

Um jetzt aber die Eigenschwingungen zu finden müsste ich diese ja lösen und ich habe leider keine Ahnung wie ich da ansetzten soll oder ob das überhaupt möglich ist.
Ich freue mich über jede Hilfe smile

Myon · Anmeldungsdatum: 04.12.2013 Beiträge: 5871

Kannst Du mal die Lagrangefunktion angeben, die Du bei a) erhalten hast? Die Bewegungsgleichungen können noch nicht richtig sein, alleine schon dimensionsmässig.
Die Bewegungsgleichungen sollte man dann auf ein Gleichungssystem der Form

bringen können. Dann die Eigenwerte und Eigenvektoren der Matrix A bestimmen. Die Eigenschwingungen sind von der Form

wobei lambda1, lambda2 die Eigenwerte und v1, v2 Eigenvektoren sind.

PILOM · Anmeldungsdatum: 11.12.2022 Beiträge: 8

Das ist meine Lagrange Funktion und die resultierenden Bewegungsgleichungen. Ich hab mal meinen ganzen Rechenweg dazu geschickt, vielleicht findest du da einen Fehler. Ich hab vielleicht schon einen Tunnelblick und übersehe etwas.
MfG Eric

Myon · Anmeldungsdatum: 04.12.2013 Beiträge: 5871

Ich denke, die Lagrange-Funktion ist grundsätzlich schon richtig, meine aber, dass man sie für kleine Winkel phi einfacher schreiben kann (bin allerdings nicht 100% sicher!):

Sonst treten in den Bewegungsgleichungen erste Ableitungen nach der Zeit auf.

Mit dieser Lagrange-Funktion ergeben sich Bewegungsgleichungen etwa wie folgt (mit sin(phi)=phi)

Mit nochmals etwas Umformen ergibt sich ein Gleichungssystem etwa wie

und man erhält die Form

Achtung, in den obigen Gleichungen sind fast sicher noch irgendwelche Fehler.

PILOM · Anmeldungsdatum: 11.12.2022 Beiträge: 8

Vielen Dank, ich sehe meinen Fehler. Ich habe die Näherung für sehr kleine phi erst auf die Bewegungsgleichungen angewandt und nicht schon auf die Lagrange Funktion. Dadurch hatte ich dann durch die Produktregel Terme drin die das DGL System kaputt/kompliziert gemacht haben.
Eine Frage hätte ich noch, darf ich den

mit 1 für kleine phi nähern oder geht das nicht?
MfG Eric

Myon · Anmeldungsdatum: 04.12.2013 Beiträge: 5871

Myon · Anmeldungsdatum: 04.12.2013 Beiträge: 5871

@PILOM: Falls Du Teil c) noch gelöst hast, mich würde interessieren, was Du erhalten hast. Oder auch, wenn Du noch eine Musterlösung erhältst.

PILOM · Anmeldungsdatum: 11.12.2022 Beiträge: 8

Myon · Anmeldungsdatum: 04.12.2013 Beiträge: 5871

Nur kurz: danke, das freut mich, denn ich erhielt die gleichen Eigenfrequenzen ;-).

Ich dachte ebenfalls, dass die Werte vernünftig aussehen, aber war mir nach der Rechnerei doch unsicher. Dass die Eigenwerte negativ sind, ist m.M.n. richtig, denn dann ergeben sich harmonische Schwingungen. Das Argument in der Exponentialfunktion wird imaginär, z.B.:

Myon · Anmeldungsdatum: 04.12.2013 Beiträge: 5871

PS: Auch für die Eigenvektoren erhalte ich Gleiches. Damit es dimensionsmässig aufgeht, könnte man schreiben

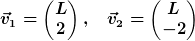
Die Eigenschwingungen haben dann die Form

mit Konstanten A_i, theta_i.

PILOM · Anmeldungsdatum: 11.12.2022 Beiträge: 8

@Myon, vielen Dank für die Hilfe, dann habe ich wohl doch nichts zu falsches gerechnet smile

Gruß Eric