| Autor |
Nachricht |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 26. Apr 2023 14:26 Titel: Mechanik und euklidische Geometrie II index_razor Verfasst am: 26. Apr 2023 14:26 Titel: Mechanik und euklidische Geometrie II |
 |
|
TomS fragt im anderen Thread:
TomS: hab den Link angepasst
| TomS hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: |
... geht es eigentlich um die Frage, ob ich in dem Hebelarm beide Endpunkte derselben Galileitransformation unterziehe oder nicht. Da gibt es nichts zu streiten, man kann es so oder so festlegen.
|
Kennst du ein Lehrbuch, das die Mechanik auf derartigen invarianten Größen aufbaut? Ich meine nicht nur speziell das Drehmoment sondern die gesamte Lagrangesche Mechanik.
|
Ich kenne kein Buch, das den Fokus auf Lagrangesche Mechanik legt oder ausführlich die Newtonsche Mechanik kovariant beschreibt. Ich kenne nur ein Buch, das eine geometrische Formulierung der klassischen Physik anstrebt, nämlich Thorne, Blandford, Modern Classical Physics. (Die Punktmechanik umfaßt aber nur gut 30 von über 1400 Seiten und ist recht elementar.) Für das Verständnis der Geometrie der Mechanik fand ich aber in erster Linie das Buch von Dirschmid, Tensoren und Felder, sehr hilfreich. Es behandelt hauptsächlich Relativitätstheorie und Differentialgeometrie. Aber die Darstellung der affinen Geometrie fand ich auch sehr lesenswert. Damit sollte es eigentlich eine leichte Übung sein, geometrische Konstruktionen für alle mechanischen Größen anzugeben.
Oft ist es ja auch nur eine Frage wie man die Formeln liest. Wenn in elementaren Darstellungen mit mit Koordinatentupeln ) gearbeitet wird, kann man das sofort auf den Tangentialraum übersetzen gearbeitet wird, kann man das sofort auf den Tangentialraum übersetzen  . Die Abhängigkeit vom Ursprung kann man dann einfach explizit machen, indem man . Die Abhängigkeit vom Ursprung kann man dann einfach explizit machen, indem man

setzt, was im affinen Raum immer möglich ist. Das beinhaltet praktisch nicht mehr als in jeder Formel geeignet einen Ortsvektor 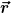 durch einen Punkt P zu ersetzen oder wenn eine vektorielle Größe benötigt wird, eben durch einen Verschiebungsvektor zwischen zwei Punkten. Das ist immer eindeutig, wenn man sich strikt an die Regeln der affinen Geometrie hält. durch einen Punkt P zu ersetzen oder wenn eine vektorielle Größe benötigt wird, eben durch einen Verschiebungsvektor zwischen zwei Punkten. Das ist immer eindeutig, wenn man sich strikt an die Regeln der affinen Geometrie hält.
Speziell für das Drehmoment  erhält man damit die allgemeine geometrische Konstruktion erhält man damit die allgemeine geometrische Konstruktion
\wedge \vec{F})
eines Bivektors auf dem Euklidischen Raum mit beliebigem Bezugspunkt O. Das Transformationsverhalten unter Änderung des "Ursprungs" O ist ein Spezialfall, der sich sofort aus der allgemeingültigen Beziehung
 + (O-O')) , ,
ergibt, die für beliebige Punkte P, O und O' gilt. Damit folgt (P wird fix gelassen, nur O wird ersetzt)
\wedge \vec{F} = M + \vec{d}\wedge\vec{F},)
m.a.W. es ist exakt dasselbe wie eine Änderung des Bezugspunkts für das Drehmoment von 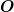 auf auf  mit der impliziten Änderung des Ortsvektors mit der impliziten Änderung des Ortsvektors  . Nur interpretiert man es als "Transformationsgesetz", wenn man O und O' als Ursprung eines Koordinatensystems betrachtet. Aber wieder ist dies kein mathematischer Unterschied, sondern nur ein unwesentlicher Unterschied in der Sichtweise. . Nur interpretiert man es als "Transformationsgesetz", wenn man O und O' als Ursprung eines Koordinatensystems betrachtet. Aber wieder ist dies kein mathematischer Unterschied, sondern nur ein unwesentlicher Unterschied in der Sichtweise.
Manchmal ist es aber auch nützlich globale Galilei-Transformationen des gesamten Raums zu betrachten, nämlich  für alle Punkte P des Raums. Hier erlaube ich noch eine Drehung für alle Punkte P des Raums. Hier erlaube ich noch eine Drehung  um den Punkt Q, um den Punkt Q,
)
mit der normalen vektoriellen Drehung  auf dem Tangentialraum. Ich würde behaupten, für Symmetrieüberlegungen ist dies sogar der üblichere Fall. Damit erhält man dann ein anderes Transformationsgesetz desselben Drehmoments, nämlich auf dem Tangentialraum. Ich würde behaupten, für Symmetrieüberlegungen ist dies sogar der üblichere Fall. Damit erhält man dann ein anderes Transformationsgesetz desselben Drehmoments, nämlich
\wedge R\cdot\vec{F} = R\cdot((P- Q) - (O-Q))\wedge R\cdot \vec{F} = R\cdot\vec{r}\wedge R\cdot\vec{F},)
was in beliebigen Dimensionen invariant unter reinen Boosts und Translationen und im 2dimensionalen unter der gesamten Galileigruppe ist.
So kannst du im Prinzip denke ich problemlos auch die ganze Lagrangesche Mechanik aufbauen. Aus ) wird wird  = V(P)) . Und die Lagrangefunktion eines Teilchens lebt auf dem Tangentialbündel . Und die Lagrangefunktion eines Teilchens lebt auf dem Tangentialbündel 
 = \frac{m}{2}\langle \dot P, \dot P\rangle - V(P))
mit Skalarprodukt  auf dem Tangentialraum auf dem Tangentialraum 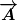 etc. etc.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 26. Apr 2023 14:52 Titel: TomS Verfasst am: 26. Apr 2023 14:52 Titel: |
 |
|
Vielen Dank!
Zwei Frage habe ich noch:
1) wie sieht dann Drehimpuls und dessen Zusammenhang mit dem Drehmoment aus?
2) wie verhält es sich bei Boosts? damit sich der Streitpunkt erledigt, müsste das Drehmoment auch invariant unter Galilei-Boosts sein
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 26. Apr 2023 16:29 Titel: index_razor Verfasst am: 26. Apr 2023 16:29 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Zwei Frage habe ich noch:
1) wie sieht dann Drehimpuls und dessen Zusammenhang mit dem Drehmoment aus?
|
Nicht anders, als du denkst, aber mit ein paar notwendigen Qualifizierungen. Der Drehimpuls ist ebenfalls ein Bivektor (oder eben ein Vektor im 3dimensionalen), der einen Bezugspunkt benötigt, definiert durch
\wedge \vec{p}.)
Natürlich ergibt sich hier noch eine Subtilität durch den Impuls, die für die Kraft nicht vorhanden ist. Der Impuls selbst erfordert auch einen Bezug. Das kann man ignorieren, wenn man kein theoretisches Problem mit absoluter Ruhe hat. (Darüber haben wir an anderer Stelle schon mal geredet). In diesem Fall gilt einfach  und folglich und folglich 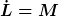 , wenn man einen "Raumfesten" (=absolut ruhenden) Bezugspunkt O wählt (also , wenn man einen "Raumfesten" (=absolut ruhenden) Bezugspunkt O wählt (also  ). Andernfalls muß man eben berücksichtigen, daß der Impuls immer auf die Bewegung eines Bezugskörper angegeben werden muß. ). Andernfalls muß man eben berücksichtigen, daß der Impuls immer auf die Bewegung eines Bezugskörper angegeben werden muß.
Eine andere Möglichkeit -- und wohl auch die natürlichste, die sich am ehesten mit der elementaren Mechanik deckt -- ist, den Ort und und die Geschwindigkeit auf denselben Bezugskörper mit Bahnkurve ) zu beziehen. Dann kann man den Impuls von P relativ zu Q definieren als zu beziehen. Dann kann man den Impuls von P relativ zu Q definieren als ) und der zugehörige Drehimpuls ist und der zugehörige Drehimpuls ist
 - Q(t))\wedge \vec{p}_Q)
Dann gilt wieder (dasselbe M wie oben)
 , ,
wenn der Bezugskörper eine geradlinig-gleichförmige Bewegung ausführt, da in diesem Fall
 = m\ddot{P} = \vec{F})
Diese Definition ist äquivalent zum "relativen Drehimpuls", die vorige zum "absoluten Drehimpuls" aus dem Artikel "Comments on Torque Analyses", den du im anderen Thread zitiert hast. Der Artikel betrachtet anscheinend wegen dieser beiden Möglichkeiten die Definition als mehrdeutig. Aber wie gesagt, wirklich natürlich ist nur die zweite und es ist auch die einzige, die sich auf die Newtonsche Raumzeit verallgemeinern läßt, in der sich keine absolute Ruhe mehr definieren läßt. Denn die zweite Definition erfordert nur, daß der Bezugskörper geradlinig-gleichförmig bewegt ist, was auch in der Raumzeit eine sinnvolle Bedingung ist.
| Zitat: | | 2) wie verhält es sich bei Boosts? damit sich der Streitpunkt erledigt, müsste das Drehmoment auch invariant unter Galilei-Boosts sein |
Der relative Drehimpuls  (zweite Definition) ist manifest invariant unter globalen Boosts, genau wie M. (zweite Definition) ist manifest invariant unter globalen Boosts, genau wie M.
Wenn nur der Bezugskörper geboostet wird (="Wechsel des Bezugssystems"),
 = Q(t) + \vec{v}t, \qquad \vec{r}' = P-Q' = (P - Q) - \vec{v}t = \vec{r} - \vec{v}t)
transformiert  anders als M, aber in einer Weise, daß wieder anders als M, aber in einer Weise, daß wieder

gilt. Denn
\wedge (\vec{p}_Q - m\vec{v}) = L_Q - \vec{v}t\wedge \vec{p}_Q - \vec{r}\wedge m\vec{v})
Also

Den absoluten Drehimpuls überlasse ich dir. ;-)
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 26. Apr 2023 17:01 Titel: TomS Verfasst am: 26. Apr 2023 17:01 Titel: |
 |
|
Vielen Dank.
Das hier ...
| index_razor hat Folgendes geschrieben: | | Sonnenwind hat Folgendes geschrieben: | | Also sagen Physiker und Techniker letztlich dasselbe aus. |
Ja, das stimmt, wenn du das Drehmoment bzgl. eines fixen Punkts definierst, wie in Gl. (11) aus dem Artikel, den TomS oben verlinkt hatte. Die n-dimensionale Verallgemeinerung dieser Gleichung lautet
\wedge \vec{F}_i.)
Unter simultanen Galileitransformationen aller (!) 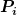 , , 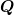 und und 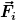 hängt die Änderung von hängt die Änderung von 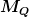 nur von der Drehung nur von der Drehung  ab, nämlich ab, nämlich
\wedge R\cdot\vec{F}_i.)
In zwei Dimensionen vereinfacht sich das zu
\sum_i (P_i -Q) \wedge \vec{F}_i = M_Q,)
da für Drehungen 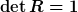 . Es kommt natürlich darauf an, ob man . Es kommt natürlich darauf an, ob man 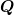 und und 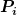 zusammen transformiert oder nur zusammen transformiert oder nur 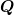 allein. allein. |
... und deine letzten Ausführungen ist eine Sichtweise, die ich tatsächlich so noch nicht kannte.
Ich beziehe mich auf Darstellungen wie
https://cimec.org.ar/foswiki/pub/Main/Cimec/MecanicaRacional/84178116-Vol-1-Landau-Lifshitz-Mechanics-3Rd-Edition-197P.pdf
Landau / Lifshitz: Mechanics
3rd ed., chap. II § 9.
Wie verträgt sich die von dir entwickelte Darstellung mit der Algebra der Galilei-Transformation? Du führst ja andere Objekte ein, die sich nur nur noch unter Rotationen transformieren.
Wie geht man sinnvollerweise bzgl. Lagrangefunktion, Euler-Lagrange-Gleichungen, Symmetrien und Noether-Theorem vor? Du hast das oben kurz skizziert, aber das wäre ja noch explizit aufzubereiten. Wozu? Nur für die Frage des Drehmoments? Ich denke, man verwendet - ähnlich wie beim Kreisel das rotierende Bezugsystem - diese explizite Mitführung eines zeitabhängigen Ursprungs nur für spezielle Fragestellungen. Oder siehst du weitere Vorteile, die gesamte Mechanik so darzustellen?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Apr 2023 06:56 Titel: index_razor Verfasst am: 28. Apr 2023 06:56 Titel: |
 |
|
Das stimmt nicht ganz. Es verhält sich so: Ich betrachte die Wirkung der Galileigruppe auf einem 4-dimensionalen affinen Raum  mit Tangentialraum mit Tangentialraum  , der die Summe aus einem eindimensionalen Vektorraum , der die Summe aus einem eindimensionalen Vektorraum 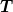 und einem dreidimensionalen euklidischen Vektorraum und einem dreidimensionalen euklidischen Vektorraum  ist. Das heißt für ist. Das heißt für  gilt ganz normal unter Galileitransformationen gilt ganz normal unter Galileitransformationen
: x \mapsto t\vec{e}_0 + R\cdot\vec{r} - \vec{u}t.\qquad\text{(1)})
Für die üblichen mechanischen Größen gebe ich eine geometrische Konstruktion auf  an. Die Wirkung der Galileigruppe auf an. Die Wirkung der Galileigruppe auf  vererbt sich dabei einfach auf diese Größen. Der Grund, weshalb z.B. die Änderung des Drehmoments vererbt sich dabei einfach auf diese Größen. Der Grund, weshalb z.B. die Änderung des Drehmoments
 - Q(t)]\wedge\vec{F}(P(t)))
nur von Rotationen abhängt, ist der, daß hier nur räumliche Vektoren auftauchen, d.h. P(t)}, \vec{F}\in \overrightarrow{E}_3) . Und die Einschränkung der Galileigruppe auf den euklidischen Teilraum . Und die Einschränkung der Galileigruppe auf den euklidischen Teilraum  besteht nur aus Rotationen. Setze einfach besteht nur aus Rotationen. Setze einfach  in Gl. (1) (oder siehe z.B. Dirschmid a.a.O., S. 227). Deswegen halte ich auch dieses Transformationsgesetz aus mathematischer Sicht für das natürlichere. Die Alternative entspricht eher einer Änderung des Bezugspunkts in Gl. (1) (oder siehe z.B. Dirschmid a.a.O., S. 227). Deswegen halte ich auch dieses Transformationsgesetz aus mathematischer Sicht für das natürlichere. Die Alternative entspricht eher einer Änderung des Bezugspunkts ) . (Was nicht heißen soll, daß diese Änderung physikalisch unwichtig ist, siehe unten.) . (Was nicht heißen soll, daß diese Änderung physikalisch unwichtig ist, siehe unten.)
| Zitat: |
Wie geht man sinnvollerweise bzgl. Lagrangefunktion, Euler-Lagrange-Gleichungen, Symmetrien und Noether-Theorem vor? Du hast das oben kurz skizziert, aber das wäre ja noch explizit aufzubereiten.
|
Die Definition der Lagrange-Funktion  erfordert ja zunächst mal die Einführung eines Phasenraums. Dafür benötigt man eigentlich schon einen Bezugskörper, weil erfordert ja zunächst mal die Einführung eines Phasenraums. Dafür benötigt man eigentlich schon einen Bezugskörper, weil  ja von den Geschwindigkeiten abhängt. Allerdings bringt es natürlich wirklich meistens nichts, die Bahnkurve dieses Körpers explizit durch die Gleichungen zu schleifen. Man muß sich nur daran erinnern, daß ein Wechsel dieses Bezugskörpers ja von den Geschwindigkeiten abhängt. Allerdings bringt es natürlich wirklich meistens nichts, die Bahnkurve dieses Körpers explizit durch die Gleichungen zu schleifen. Man muß sich nur daran erinnern, daß ein Wechsel dieses Bezugskörpers  = Q(t) + \vec{c}(t)) dem Übergang zu einer anderen Lagrangefunktion entspricht, z.B. dem Übergang zu einer anderen Lagrangefunktion entspricht, z.B.

(Der Term  ist eine totale Zeitableitung und spielt keine Rolle.) Aber wenn man keinen solchen Wechsel vorhat, muß man Q auch überhaupt nicht weiter erwähnen. (Dann landet man bei der Sichtweise am Ende meines ersten Beitrags.) Noether-Theorem, Euler-Lagrange-Gleichungen funktionieren, höchstens abgesehen von der Notation, noch genauso. Die Untersuchung der Boostinvarianz erfordert z.B. eine Änderung des Bezugs, ansonsten passiert physikalisch nichts interessantes. ist eine totale Zeitableitung und spielt keine Rolle.) Aber wenn man keinen solchen Wechsel vorhat, muß man Q auch überhaupt nicht weiter erwähnen. (Dann landet man bei der Sichtweise am Ende meines ersten Beitrags.) Noether-Theorem, Euler-Lagrange-Gleichungen funktionieren, höchstens abgesehen von der Notation, noch genauso. Die Untersuchung der Boostinvarianz erfordert z.B. eine Änderung des Bezugs, ansonsten passiert physikalisch nichts interessantes.
***
Dies alles bringt für mich in erster Linie mehr Klarheit in die mathematische Struktur der Mechanik. Die Definition von Inertialsystemen, die Rolle von Scheinkräften sind neben der Frage nach dem Transformationsverhalten häufig aufgeworfene Probleme, die oft für Durcheinander sorgen. Ich denke das liegt genau daran, daß man in der Formulierung der Mechanik nicht explizit auf die Existenz von Bezugskörpern und oft nichtmal auf die Existenz einer verwendeten Basis hinweist. Betrachten man z.B. den "Ortsvektor" ) und definiert die "Geschwindigkeit" und definiert die "Geschwindigkeit" ) wird mit meiner Übersetzungsprozedur in Größen der euklidischen Geometrie sofort eine Mehrdeutigkeit klar: Der Vektor ist wird mit meiner Übersetzungsprozedur in Größen der euklidischen Geometrie sofort eine Mehrdeutigkeit klar: Der Vektor ist
})
aber was ist dann 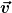 -- --

oder

Ausgehend von Gl (2) und der Definition "Geschwindigkeit ist die Ableitung des Ortsvektors nach der Zeit" kann nur die zweite Gleichung gemeint sein. Aber stattdessen wird oft die erste verwendet. Das ist auch klar, denn die zweite Gleichung kann man allein mit Koordinatentupeln nicht mal ausdrücken. Das ist inkonsistent, und diese Inkonsistenz pflanzt sich auf die Definition der Beschleunigung fort. Für zeitunabhängige Basen, liefern beide Definitionen dasselbe Ergebnis, was oft zu der Aussage führt, die Bewegungsgesetze der Mechanik gelten nur in Inertialsystemen. Aber das macht die Sache nicht einfacher, sondern komplizierter und obskurer. Das Ergebnis dieser Konfusion kann man auch in einigen Threads hier im Forum betrachten.
Wenn man stattdessen sowohl die Abhängigkeit von der Basis (sofern überhaupt eine verwendet wird, was oft gar nicht nötig ist) als auch von der Bahn des Bezugskörpers explizit macht, lösen sich alle diese Probleme ganz trivial auf, und die Eigenschaften der Bewegungsgesetze werden m.E. viel natürlicher und intuitiver.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 28. Apr 2023 08:49 Titel: TomS Verfasst am: 28. Apr 2023 08:49 Titel: |
 |
|
Wahrscheinlich sehe ich den Wald vor lauter Bäumen nicht.
1) Üblicherweise hat man



L folgt mittels Norther-Theorem (z.B. für das freie Teilchen). M ist letztlich eine Definition, das letzte Gleichheitszeichen folgt aus den Bewegungsgleichungen.
Diese Größen gelten nach meinem Verständnis für einen festen Koordinatenursprung.
Die Galilei-Transformation besagt nun, dass die bekannten Regeln für Translation, Rotation und Boost gelten. Dies entspricht einer Transformation des Bezugsystems.
2) Bei dir gilt nun - und das war ja die eigentliche Frage -
 \times F)
wobei du nun r und o zugleich einer Galilei-Transformation unterwirfst, wobei der Abstandsvektor (r - o) invariant bzgl. Translation und Boost ist.
Diese Definition des Drehmoments kann ich einführen, ohne mir irgendwelche Gedanken über eine andere Formulierung zu machen oder meine o.g. Lagrangefunktion zu ändern. Ich definiere
 \times F)
und verstehe diese Größe - so wie beim starren Körper - im mitbewegten Bezugsystem.
Meine Frage ist aber eine andere: wie gelange ich von einer Lagrangefunktion zu dieser Definition des Drehmoments?
Dazu muss ich doch anstelle von

jetzt

betrachten.
D.h. aber doch, ich muss auf dieser Basis neue Größen für p, L, F und M berechnen. Das war meine Frage.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 28. Apr 2023 09:24, insgesamt einmal bearbeitet |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Apr 2023 09:13 Titel: index_razor Verfasst am: 28. Apr 2023 09:13 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Wahrscheinlich sehe ich den Wald vor lauter Bäumen nicht.
1) Üblicherweise hat man



L folgt mittels Norther-Theorem (z.B. für das freie Teilchen). M ist letztlich eine Definition, das letzte Gleichheitszeichen folgt aus den Bewegungsgleichungen.
Diese Größen gelten nach meinem Verständnis für einen festen Koordinatenursprung.
Die Galilei-Transformation besagt nun, dass die bekannten Regeln für Translation, Rotation und Boost gelten. Dies entspricht einer Transformation des Bezugsystems.
2) Bei dir gilt nun - und das war ja die eigentliche Frage -
 \times F)
|
Nein, bei mir gilt einfach  . Ich betrachte also absolut dasselbe M . Ich betrachte also absolut dasselbe M
\times\vec{F}) . .
Die Frage war nur, "wie transformiert M unter der Galileigruppe". Eine möglich Antwort ist: Man betrachtet die Wirkung der Gruppe auf der affinen Raumzeit und transformiert alle Punkte, also auch P und O. Da  ein räumlicher Vektor ist, bleibt dann nur eine Rotation ein räumlicher Vektor ist, bleibt dann nur eine Rotation

Oder eine andere Möglichkeit: man ändert den Bezugskörper O durch einen relativ zu diesem geradlinig gleichförmig bewegten Bezugskörper und läßt P fix (oder umgekehrt). Dann erhalte ich z.B.

mit einem entsprechenden Zusatzterm  im transformierten Drehmoment. Das ist schon alles. Ich halte die Frage, welche dieser beiden Möglichkeiten die richtige ist, für falsch gestellt. im transformierten Drehmoment. Das ist schon alles. Ich halte die Frage, welche dieser beiden Möglichkeiten die richtige ist, für falsch gestellt.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 28. Apr 2023 12:05 Titel: TomS Verfasst am: 28. Apr 2023 12:05 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Das ist schon alles. Ich halte die Frage, welche dieser beiden Möglichkeiten die richtige ist, für falsch gestellt. |
Es geht nicht um richtig oder falsch, da hast du recht. Aber es ist sicher nicht schon alles ;-)
Zum Drehimpuls:

1) deine Herangehensweise zu Translation und Boost



2) mir bekannte Herangehensweise


 \times (p - mu))
Bei deiner Vorgehensweise (1) sind r, p und L invariant bzgl. Translation und Boost, und transformieren bzgl. Rotationen wir Vektoren. D.h. wir reden von einer Darstellung der SO(3).
Bei der üblichen Vorgehensweise (2) transformieren r, p und L bzgl. der vollen Galilei-Gruppe.
(1) ist nicht falsch, es erscheint mir im Allgemeinen jedoch unnatürlich. Im Speziellen - wenn ich nur auf das Drehmoment hinaus will - dann OK. Zumindest ist (1) nicht verbreitet. Ich kenne auch keine entsprechende Einführung der Poincare-Gruppe im Falle der SRT.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Apr 2023 12:29 Titel: index_razor Verfasst am: 28. Apr 2023 12:29 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
(1) ist nicht falsch, es erscheint mir im Allgemeinen jedoch unnatürlich. Im Speziellen - wenn ich nur auf das Drehmoment hinaus will - dann OK. Zumindest ist (1) nicht verbreitet. Ich kenne auch keine entsprechende Einführung der Poincare-Gruppe im Falle der SRT. |
Doch in der SRT geht es genauso. Und es gibt einige moderne Darstellungen, die es genauso machen. Dort ist es nämlich noch einfacher, weil die Struktur der Raumzeit simpler ist. Es handelt sich um einen affinen Raum  mit 4-dimensionalem pseudoeuklidischen Tangentialraum. Poincare-Transformationen sind genau die affinen Transformationen auf mit 4-dimensionalem pseudoeuklidischen Tangentialraum. Poincare-Transformationen sind genau die affinen Transformationen auf  , deren Differential , deren Differential  die linearen Transformationen des Tangentialraums mit der Eigenschaft die linearen Transformationen des Tangentialraums mit der Eigenschaft  = g(x,y)) sind. sind.
Alles was ich tue, ist diese Situation in kompletter Analogie auf die Galileische Raumzeit zu übertragen. (Siehe nochmal hier für eine etwas genauere Erklärung wie diese Analogie aussieht. Noch ausführlicher, wie gesagt, in dem Buch von Dirschmid.)
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 28. Apr 2023 13:23 Titel: TomS Verfasst am: 28. Apr 2023 13:23 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Doch in der SRT geht es genauso. Und es gibt einige moderne Darstellungen, die es genauso machen. |
Ich bestreite doch nicht, dass es funktioniert; ich halte die Vorgehensweise lediglich für wenig verbreitet. Kennst du eine online verfügbare Quelle?
Und wie gesagt, ich halte es für unnatürlich, wenn Rotationen anders behandelt werden. Oder sieht das nur so aus? Dann habe ich noch irgendwas nicht verstanden.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Apr 2023 13:55 Titel: index_razor Verfasst am: 28. Apr 2023 13:55 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Doch in der SRT geht es genauso. Und es gibt einige moderne Darstellungen, die es genauso machen. |
Ich bestreite doch nicht, dass es funktioniert; ich halte die Vorgehensweise lediglich für wenig verbreitet. Kennst du eine online verfügbare Quelle? |
Ja, an der Verbreitung kann ich allein natürlich nicht viel ändern. Ich kann nur versuchen klar zu machen, warum ich diese Darstellung für überlegen halte. Aber es kann auch an der Auswahl der Literatur liegen. Wie gesagt, für die SRT ist sie wohl verbreiteter als für die Newtonsche Mechanik. Eine Online-Quelle kenne ich auch leider nicht. (Ich suche selten Online-Skripte zu diesem Thema.)
| Zitat: |
Und wie gesagt, ich halte es für unnatürlich, wenn Rotationen anders behandelt werden. Oder sieht das nur so aus? Dann habe ich noch irgendwas nicht verstanden. |
Ja, das sieht wohl nur so aus. Wie gesagt, ich betrachte eine Wirkung der vollen Galileigruppe -- inklusive Boosts, Rotationen und Translationen -- auf der Galileischen Raumzeit. Kein Element der Gruppe wird dabei irgendwie gesondert behandelt. Daraus folgen die angegebenen Transformationsgesetze ganz natürlich. Sie sind eine direkte Folge der Definition: Eine Galileitransformation (Poincare-Transformation) ist eine affine Abbildung der Raumzeit, die die galileische Struktur (pseudoeuklidische Struktur) erhält. Unter dem "Erhalten" der galileischen Struktur wird dabei verstanden: Zeitintervalle zwischen beliebigen Ereignissen bleiben gleich und räumliche Abstände zwischen gleichzeitigen Ereignissen bleiben gleich. (Beides ist der Grund, warum räumliche Vektoren nur rotiert werden können.) Mehr habe ich nicht vorausgesetzt. Und diese Definition von Galileitransformation ist absolut natürlich.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 28. Apr 2023 14:17 Titel: TomS Verfasst am: 28. Apr 2023 14:17 Titel: |
 |
|
Stimme dir bei alledem zu.
Aber kannst du mir dann erklären, wie du dies hier
| index_razor hat Folgendes geschrieben: | Manchmal ist es aber auch nützlich globale Galilei-Transformationen des gesamten Raums zu betrachten, nämlich  für alle Punkte P des Raums. Hier erlaube ich noch eine Drehung für alle Punkte P des Raums. Hier erlaube ich noch eine Drehung  um den Punkt Q, um den Punkt Q,
)
mit der normalen vektoriellen Drehung  auf dem Tangentialraum. Ich würde behaupten, für Symmetrieüberlegungen ist dies sogar der üblichere Fall. Damit erhält man dann ein anderes Transformationsgesetz desselben Drehmoments, nämlich auf dem Tangentialraum. Ich würde behaupten, für Symmetrieüberlegungen ist dies sogar der üblichere Fall. Damit erhält man dann ein anderes Transformationsgesetz desselben Drehmoments, nämlich
\wedge R\cdot\vec{F} = R\cdot((P- Q) - (O-Q))\wedge R\cdot \vec{F} = R\cdot\vec{r}\wedge R\cdot\vec{F},)
|
interpretierst?
Das meinte ich mit einer Sonderstellung der Rotation (mir ist natürlich klar, wie man das berechnet).
Wie soll ich es formulieren? In der üblichen Darstellung überträgt sich die volle Algebra auch auf andere Objekte; z.B. in der SRT transformiert der Energie-Impuls-Vierervektor exakt so wie der Raumzeit-Vektor. In deiner Darstellung treten Größen auf, die bzgl. gewisser Galilei-Transformationen Skalare sind, bzgl. Drehungen jedoch Vektoren; das ist erst mal ungewöhnlich.
Oder sagst du, dass lediglich eine speziell konstruierte Größe M ein spezielles Transformationsverhalten aufweist? Bzw. dass die Raumzeit eine kompliziertere Struktur hat?
Ja, letzteres stimmt natürlich. Evtl. erscheint die Herangehensweise in der SRT tatsächlich natürlicher, und man erkennt, dass gewisse Artefakte nur der der Group Contraction von Poincare zu Galilei geschuldet sind.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Apr 2023 14:54 Titel: index_razor Verfasst am: 28. Apr 2023 14:54 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Stimme dir bei alledem zu.
Aber kannst du mir dann erklären, wie du dies hier
| index_razor hat Folgendes geschrieben: | Manchmal ist es aber auch nützlich globale Galilei-Transformationen des gesamten Raums zu betrachten, nämlich  für alle Punkte P des Raums. Hier erlaube ich noch eine Drehung für alle Punkte P des Raums. Hier erlaube ich noch eine Drehung  um den Punkt Q, um den Punkt Q,
)
mit der normalen vektoriellen Drehung  auf dem Tangentialraum. Ich würde behaupten, für Symmetrieüberlegungen ist dies sogar der üblichere Fall. Damit erhält man dann ein anderes Transformationsgesetz desselben Drehmoments, nämlich auf dem Tangentialraum. Ich würde behaupten, für Symmetrieüberlegungen ist dies sogar der üblichere Fall. Damit erhält man dann ein anderes Transformationsgesetz desselben Drehmoments, nämlich
\wedge R\cdot\vec{F} = R\cdot((P- Q) - (O-Q))\wedge R\cdot \vec{F} = R\cdot\vec{r}\wedge R\cdot\vec{F},)
|
interpretierst?
Das meinte ich mit einer Sonderstellung der Rotation (mir ist natürlich klar, wie man das berechnet).
|
Ich glaube ich weiß was du meintest. Aber das liegt eben daran, daß 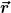 ein räumlicher Vektor ist. Er verbindet also gleichzeitige Ereignisse. Sein Bild unter Galileitransformation verbindet wieder gleichzeitige Ereignisse und hat dieselbe Länge wie ein räumlicher Vektor ist. Er verbindet also gleichzeitige Ereignisse. Sein Bild unter Galileitransformation verbindet wieder gleichzeitige Ereignisse und hat dieselbe Länge wie 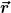 , denn das ist genau die Struktur, die unter Galileitransformationen erhalten bleibt. Und daraus folgt sofort, daß , denn das ist genau die Struktur, die unter Galileitransformationen erhalten bleibt. Und daraus folgt sofort, daß 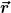 nur rotiert worden sein kann. nur rotiert worden sein kann.
| Zitat: |
Wie soll ich es formulieren? In der üblichen Darstellung überträgt sich die volle Algebra auch auf andere Objekte; z.B. in der SRT transformiert der Energie-Impuls-Vierervektor exakt so wie der Raumzeit-Vektor. In deiner Darstellung treten Größen auf, die bzgl. gewisser Galilei-Transformationen Skalare sind, bzgl. Drehungen jedoch Vektoren; das ist erst mal ungewöhnlich. |
Nein, das stimmt so nicht. Impulse sind in der Newtonschen Mechanik räumliche Vektoren. Sie transformieren genauso wie alle räumlichen Vektoren in der Raumzeit. In der SRT ist der Viererimpuls ein zeitartiger Vektor, und er transformiert genauso wie alle zeitartigen Vektoren. Das ist vollkommen analog. Die einzigen Unterschiede, die es hier gibt, sind in den unterschiedlichen geometrischen Strukturen der Galilei- und der Minkowskiraumzeit begründet. Sie haben nichts mit der Behandlung der Gruppenwirkung zu tun.
| Zitat: |
Oder sagst du, dass lediglich eine speziell konstruierte Größe M ein spezielles Transformationsverhalten aufweist? Bzw. dass die Raumzeit eine kompliziertere Struktur hat? |
Ja, die Galileische Raumzeit hat eine komplizierter Struktur. Es gibt einen absoluten Unterschied zwischen zeitlichen und räumlichen Vektoren. Ein rein zeitlicher Vektor transformiert gemäß
: \vec{e}_0\mapsto \vec{e}_0 + \vec{u})
und bleibt unbeeinflußt von der Rotation. (Allerdings gilt: ^{-1} = (R^{-1}, -R^{-1}\cdot\vec{u})) .) Ein rein räumlicher Vektor transformiert wie .) Ein rein räumlicher Vektor transformiert wie
: \vec{r} \mapsto R\cdot\vec{r})
und wird nur rotiert. Die Transformation von Linearkombinationen zeitlicher und räumlicher Vektoren ergibt sich aus der Linearität der Galileitransformation.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 28. Apr 2023 15:05 Titel: TomS Verfasst am: 28. Apr 2023 15:05 Titel: |
 |
|
Ok, klar. Danke.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 29. Apr 2023 11:25 Titel: index_razor Verfasst am: 29. Apr 2023 11:25 Titel: |
 |
|
Vielleicht noch ein paar Bemerkungen um klar zu machen, daß es sich bei den verschiedenen Transformationsverhalten mechanischer Größen nicht um vollkommen konträre Auffassung von Mechanik, der Wirkung der Galileigruppe etc. handelt. Es sind eigentlich nicht mal fundamental verschiedene Auffassungen, sondern bloße Festlegungen, welche Art von Änderung am System man gerade untersuchen will.
Für zwei Punkte P und Q mit räumlichem Verbindungsvektor  erhalten wir mittels Galileitransformation erhalten wir mittels Galileitransformation 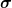 die Beziehungen die Beziehungen
} = R\cdot\vec{r} + \vec{v}t + \vec{d}\qquad\text{(a)})
P} = R\cdot\vec{r} - \vec{u}t - \vec{d}\ \ \text{mit}\ \ t(\vec{u} - \vec{v}) = R\cdot\vec{r} - \vec{r}\qquad\text{(b)}) , ,
sowie
\sigma(P)} = R\cdot\vec{r}\qquad\text{(c)}) . .
Daraus ergeben sich drei mögliche Transformationsgesetze für das Drehmoment  , nämlich , nämlich
\sigma(P)}\times\vec{F}' = R\cdot\vec{r}\times R\cdot\vec{F})
P}\times\vec{F}' = M' - (\vec{u}t + \vec{d})\times R\cdot\vec{F})
und
} \times\vec{F}' = M' + (\vec{v}t + \vec{d})\times R\cdot{F})
Etwas längliche Herleitung aus der Galileischen Struktur der Raumzeit:
Zur Erinnerung: die Welt ist ein 4-dimensionaler affiner Raum  mit Tangentialraum mit Tangentialraum  . Auf dem Tangentialraum gibt es ein lineares Funktional . Auf dem Tangentialraum gibt es ein lineares Funktional 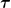 mit mit  = 0) , das die absolute Zeit zwischen zwei Punkten in , das die absolute Zeit zwischen zwei Punkten in  angibt. angibt.
Betrachten wir zwei gleichzeitige Punkte  , d.h. , d.h.  . Beide Punkte sollen zu irgendeiner Zeit t später als der Punkt O stattfinden. Es gibt also zwei Vektoren, sagen wir . Beide Punkte sollen zu irgendeiner Zeit t später als der Punkt O stattfinden. Es gibt also zwei Vektoren, sagen wir  , mit , mit  = \tau(e_0') = 1) , so daß , so daß
 und und 
Nun untersuchen wir, was bei einer Galileitransformation  dieser Punkte passiert und wie sich ihre geometrischen Beziehungen zueinander ändern. Eine Galileitransformation ändert nicht die Zeitintervalle zwischen zwei Punkten. Folglich ist der Vektor dieser Punkte passiert und wie sich ihre geometrischen Beziehungen zueinander ändern. Eine Galileitransformation ändert nicht die Zeitintervalle zwischen zwei Punkten. Folglich ist der Vektor \sigma(P)} \in\overrightarrow{E}_3) wieder rein räumlich. Da auch der euklidische Abstand gleichzeitiger Ereignisse nicht geändert wird, gilt wieder rein räumlich. Da auch der euklidische Abstand gleichzeitiger Ereignisse nicht geändert wird, gilt
\sigma(P)}\right\| = \|\overrightarrow{QP}\|.)
Es gibt also eine orthogonale Abbildung  mit mit
 = \sigma(Q) + R\cdot \vec{r}\qquad \text{(1)}) . .
Das ist Beziehung (c). Aus der Invarianz zeitlicher Abstände folgt ebenfalls
\sigma(O)}) = \tau(\overrightarrow{\sigma(Q)\sigma(O)}) = t)
Also gibt es zwei Vektoren  , so daß , so daß
 = \sigma(O) + t(e'_0 + \vec{u})\qquad\text{(2)})
und
 = \sigma(O) + t(e_0 + \vec{v})\qquad\text{(3)})
Die beiden Vektoren sind natürlich nicht unabhängig. Es gilt  = R\cdot\vec{r} - \vec{r}) . (Das folgt aus . (Das folgt aus  .) .)
Bisher haben wir die Galileitransformation 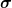 nur über die Wirkung auf den Tangentialraum charakterisiert, d.h. wir haben jeweils nur die Änderung der Verbindungsvektoren explizit angegeben. Aus dieser Festlegung erhalten wir eine eindeutige affine Abbildung auf nur über die Wirkung auf den Tangentialraum charakterisiert, d.h. wir haben jeweils nur die Änderung der Verbindungsvektoren explizit angegeben. Aus dieser Festlegung erhalten wir eine eindeutige affine Abbildung auf  , wenn wir für einen bestimmten Punkt vorgeben auf welchen Bildpunkt er durch , wenn wir für einen bestimmten Punkt vorgeben auf welchen Bildpunkt er durch 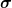 transformiert wird. Das ist der einzige Grund warum ich den Punkt O eingeführt habe, und ich lege fest, daß transformiert wird. Das ist der einzige Grund warum ich den Punkt O eingeführt habe, und ich lege fest, daß  = O + \vec{d}) mit mit  ein räumlicher Vektor. ein räumlicher Vektor.
Kombinieren wir (1) und (3) erhalten wir
 = Q + R\cdot\vec{r} + t\vec{v} + \vec{d}.)
Das ist (a). Analog folgt (b) aus (1) und (2).
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 29. Apr 2023 16:28 Titel: TomS Verfasst am: 29. Apr 2023 16:28 Titel: |
 |
|
Nochmals danke. Ja, ist letztlich Konvention, du hast recht.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
|
|















