| Autor |
Nachricht |
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18080
|
 TomS Verfasst am: 02. Feb 2024 09:57 Titel: Geometrie des Kegels - zu Raumzeit-Krümmung und Gravitation |
 |
|
Ich denke, wir sollten das Thema separat diskutieren. Evtl. passt es besser unter "Sonstiges".
Es geht im Folgenden um die Geometrie des Kegels als 2-dim. Mannigfaltigkeit, die Äquivalenz zur Konstruktion mittels Einbettung in einen 3-dim. flachen Raum. Speziell um Geodäten auf dem Kegel, die verschwindende intrinsische Krümmung, sowie den nicht-trivialen Effekt der Topologie, sozusagen der Spitze / Berandung oder Kappe.
Ziel ist letztlich die Erklärung der Effekte vollständig ohne Einbettung!
Metrik mittels Einbettung im 3-dim. Raum
Man startet mit der Lagrangefunktion des freien Teilchens in drei Dimensionen, formuliert in sphärischen Koordinaten:
)
In dieser fixiert man den Winkel theta, d.h.
und erhält
)
Daraus liest man die Metrik
 )
ab.
Metrik mittels Verkleben eines Sektors der 2-dim. Ebene
Man betrachte eine Kreisscheibe, aus der eine Sektor herausgeschnitten wurde; man verklebe die Schnittränder, ohne sich vorzustellen, wie das praktisch nur in drei Dimensionen funktioniert.
Zunächst zur Metrik der flachen 2-dim. Ebene in Polarkoordinaten:
Für Kurven gamma entlang der Koordinaten r und phi, wobei die jeweils andere Koordinate fest bleibt, gilt
 )
Das Herausschneiden des Sektors mit Winkel delta führt auf einen neuen Winkel
Durch das Verkleben der Ränder ändert sich der Umfang eines Kreises um den Ursprung von
zu
 r )
Das erreicht man ebenfalls mittels
wobei jeweils
gilt.
Die Länge in psi-Richtung ist also entsprechend verkürzt.
Damit gilt für die Metrik
 )
Die beiden Metriken sind also identisch, wenn man phi und psi identifiziert, sowie
setzt. Aus identischen Metriken folgen aber identische geometrische Eigenschaften.
Anmerkung: der letzte Ansatz ist allgemeiner, da man auch q > 1 betrachten kann.
Zuletzt bearbeitet von TomS am 04. Feb 2024 10:02, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18080
|
| TomS Verfasst am: 02. Feb 2024 11:06 Titel: |
|
|
Nächster Schritt:
Geodäten als Lösungen der Euler-Lagrange-Gleichungen
Die Euler-Lagrange-Gleichungen für das auf zwei Dimensionen reduzierte Problem lauten
Die zweite Gleichung formen wir noch um und erhalten
Wenn ich mich nicht verrechnet habe, entspricht das der Geodätengleichung, aus der sich die Christoffel-Symbole (unter der Beachtung von Symmetrie in b, c, d.h. zwei gemischte Terme ablesen lassen:
)
(alle anderen Null)
Der nicht-triviale Effekt des Herausschneidens und Verklebens steckt also im Sinus-Term.
Die Lösung der Gleichungen ist im folgenden eher weniger relevant. Wichtig ist lediglich, dass
keine Lösung darstellt, d.h. ein Kreis mit konstantem Radius ist keine Geodäte. Die Ursache ist liegt nicht in der Konstruktion des Kegels sondern bereits in der Geometrie der Ebene begründet: Geodäten sind Geraden; für konstantes phi entspricht dies radialen Geraden; für Geraden zwischen zwei Punkten mit unterschiedlichen Winkeln phi ist der Radius r entlang dieser Geraden nie konstant.
Geodäten mittels Levi-Civita-Zusammengang
Hier verwendet man die Definition
 )
sowie das obige Resultat
 )
 )
Die Berechnung ist unübersichtlicher, man muss insbs. Symmetrie-Argumente benutzen, um den Aufwand zu reduzieren.
Ein Beispiel:
für a=r muss wg. der Form von g auch d=r gelten;
dann muss in den ersten beiden Termen c=r bzw. b=r sein;
aber die rr-Komponente von g ist konstant, also folgt Null;
damit kann nur der letzte Term beitragen;
wg. der Ableitung nach d=r muss also b=c=psi sein, sonst Null
Daraus folgt als nicht-verschwindender Term für a=r
 = - \frac{1}{2} \partial_r \, r^2 \, q^2 = - r \, q^2)
(Rest analog)
Hier steckt der nicht-triviale Effekt des Herausschneidens und Verklebens in q, was bei verschwindendem delta ja q=1 liefert.
Beide Wege führen also zu identischen Metriken und somit zu identischen Geodätengleichungen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18080
|
| TomS Verfasst am: 03. Feb 2024 07:48 Titel: |
|
|
Nun zum ursprünglichen Ansinnen, dem Paralleltransport eines Vektors entlang einer geschlossenen Kurve um die Spitze; technisch Holonomie, speziell für eine flache Mannigfaltigkeit – noch zu zeigen – Monodromie
Paralleltransport
Der Levi-Civita-Zusammenhang Gamma definiert eine kovariante Ableitung von Vektorfeldern A auf Riemannschen Mannigfaltigkeiten. Der Paralleltransport entlang einer Kurve gamma
 )
wird definiert mittels des Tangenten-Einheitsvektors der Kurve
bzgl. eines geeigneten Parameters tau, so dass
gilt, sowie der kovarianten Richtungsableitung
 = 0)
Dabei wird die kovariante Ableitung auf die Tangente projiziert. Man erkennt, dass vermöge
im Spezialfall A = u gerade die Geodätengleichung resultiert, d.h. eine Geodäte ist gerade so definiert, dass ihre Tangente bzgl. ihrer selbst parallel verschoben wird.
Im vorliegenden Fall des Kegels betrachten wir eine geschlossene Kurve bei festem Radius r in psi-Richtung
 = (r, \psi))
mit
 = \omega \tau)
 )
sowie wg. Normierung von u
Der Zusammenhang ist gegeben durch die oben abgeleiteten Größen
Nach Einsetzen erkennt man, dass durch die Projektion auf u lediglich die psi-Ableitung verbleibt, d.h. die r-Abhängigkeit von A ist irrelevant; außerdem liefert Gamma nur einen Beitrag, nämlich die psi-Komponente.
Für die beiden Möglichkeiten b = r, psi ein resultieren zwei gekoppelte lineare Differentialgleichungen mit jeweils einem Gamma-Term
Durch nochmaliges Differenzieren und Eliminieren des Terms mit erster Ableitung folgen zwei ungekoppelte Schwingungsgleichungen mit Frequenz; der Lösungsansatz ist demnach eine Linearkombination aus Sinus und Cosinus. Unter Beachtung der Anfangsbedingungen für A bei psi = 0 erhält man den eindeutigen Paralleltransport
 = A^r_0 \, \cos q\psi - rq A^\psi_0 \, \sin q\psi )
 = A^\psi_0 \, \cos q\psi + \frac{1}{rq} A^r_0 \, \sin q\psi )
eines beliebigen Vektors A entlang der gewählten Kurve gamma, die die Spitze bzw. Kappe des Kegels umschließt.
Allgemein erhält man eine Inverse des Paralleltransportes
Im vorliegenden Fall entspricht dies einer linearen Transformation
 = \Lambda(\psi) \, A_0)
 = \begin{pmatrix} \cos q\psi & - rq \\ \frac{1}{rq} & \cos q\psi \end{pmatrix} )
Die Forderung eines trivialen Paralleltransports führt auf
 = A^a(0))
d.h.
mit den Lösungen
Beschränken wir uns auf den ursprünglichen Fall
so erkennen wir, dass
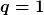
auf einen "trivialen Kegel" d.h. auf die euklidische Ebene in Polarkoordinaten führt. Andere Werte
entsprechen dagegen "echten Kegeln" mit jeweils nicht-trivialem Paralleltransport.
Interessant ist dieses Ergebnis insbs. aufgrund der Flachheit des Kegels – noch zu zeigen – im Gegensatz zu einer ähnlichen Rechnung z.B. für die Kugeloberfläche mit intrinsischer Krümmung. Es sollte außerdem klar sein, dass es sich um einen globalen topologischen Effekt handelt, da die lokale Geometrie in der Umgebung der Kurve überall identisch flach ist, und da insbs. keine "Krümmung von der Spitze oder Kappe aus wirkt".
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 05. Feb 2024 06:54, insgesamt 4-mal bearbeitet |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18080
|
| TomS Verfasst am: 04. Feb 2024 08:34 Titel: |
|
|
Der Riemannsche Krümmungstensor
Die vollständige Information zur intrinsischen Krümmung ist im Riemannschen Krümmungstensor kodiert. Er folgt unmittelbar aus dem Paralleltransport.
Betrachten wir den Paralleltransport des Vektors A über eine "infinitesimale" Strecke, deren Richtung definiert wird mittels eines konstanten Einheitsvektors u, anschließend über eine weitere infinitesimale Strecke entlang eines weiteren Vektors v; dann transportieren wir den so erhaltenen Vektor zurück entlang -a, anschließend entlang -b zum Ausgangspunkt. Dies liefert den Weg a, b, -a, -b und somit die Seiten eines infinitesimalen Parallelograms. Ausgegend vom oben diskutierten Paralleltransport
 \, dx)
erhalten wir so den Riemannschen Krümmungstensor R als Abbildung
Man kann die Vektoren u, v auch eliminieren und dies direkt mittels der kovariante Ableitung des Vektors A formulieren:
Dieser Kommutator entspricht dem Vergleich des Effektes der Geometrie auf den Vektor A entlang zweier infinitesimaler Wege beschrieben mittels (u,v) und (-v, -u)
Erweitert man die linke Seite und nutzt die torsionsfreie Eigenschaft des Christoffel-Symbols, so ergibt sich, dass
Es ist nun eine nette Übung, zu zeigen, dass diese Größe für den Kegel identisch Null ist (während sie für die Kugel eine nicht-verschwindende konstante Krümmung liefert).
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 04. Feb 2024 15:42, insgesamt 9-mal bearbeitet |
|
|
Aruna_Gast
Gast
|
| Aruna_Gast Verfasst am: 04. Feb 2024 08:52 Titel: |
|
|
| TomS hat Folgendes geschrieben: |
bzgl. eines geeigneten Parameters tau, so dass
|
Da bleibe ich schon hängen, weil ich mir die Bedeutung von kovarianten und kontravarianten Vektoren noch nicht erarbeitet habe und mir daher das Produkt nix sagt....
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18080
|
| TomS Verfasst am: 04. Feb 2024 09:20 Titel: |
|
|
Dann vergiss die Unterscheidung, sie ist eher technisch.
Ohnehin wird in den meisten Darstellungen der Physiker zu viel auf Indizes herumgeritten. Wichtiger sind die Bedeutungen der koordinatenfreien Formeln. Die Indizes braucht man nur zum konkreten Rechnen, nicht für's Verständnis, was man da berechnet. Konkret: man versteht die Idee eines Kräfteparallelogramms, der Addition zweier Geschwindigkeitsvektoren oder einer Rotation sogar besser anhand von Pfeilen ohne Indizes. Das gilt auch für meine Darstellung oben, ich werde noch etwas aufräumen.
Die Idee ist, auf einer gekrümmten Fläche, das Skalarprodukt zweier Vektoren zu definieren; dies erfordert eine Verallgemeinerung
zu
= \sum_{ab} g_{ab} x^a y^b)
D.h. das Skalarprodukt zweier Vektoren ist zunächst einfach eine lineare Abbildung g, die zwei Vektoren eine Zahl zuordnet. Speziell für y=x entspricht dies dem Quadrat des Betrages bzw. der Norm
 = \| x \|^2 )
Damit dies auf vernünftige Längen und Winkel führt, muss g für nicht-verschwindende Vektoren eine Länge ungleich Null liefern, und g soll symmetrisch in der Vertauschung von x und y sein. D.h.
 \ge 0)
 = 0 \;\implies x=0)
 = g(y,x))
(Das ändert sich in der RT, aber hier bleiben wir auf dem Kegel)
Damit ist g symmetrisch, d.h.
und damit wiederum diagonalisierbar mit strikt positiven Eigenwerten. Die Diagonalform ist natürlich wünschenswert.
Hat man diese Metrik sowie die geeigneten Koordinaten inkl. deren Gültigkeitsbereichen, so ist damit eine Riemannsche Mannigfaltigkeit inkl. aller geometrischen Eigenschaften eindeutig definiert. In unserem Fall darf man sich vorstellen, dass q die punktierte euklidische Ebene deformiert:
(Mathematiker würden hier zwei sogenannte Karten einführen)
Und damit ist schon mal das Märchen der drei Dimensionen vom Tisch.
Warum ist das wichtig? Weil es Artefakte derartiger Einbettungen gibt! Einfachstes Beispiel ist der 2-Torus, d.h. ein an gegenüberliegenden Kanten verklebtes Rechteck. Der ist flach, d.h. verschwindende Krümmung. Was man sich aber nicht vorstellen kann, wenn man sich die Einbettung anschaut; es existiert schlicht keine überall flache Einbettung des 2-Torus in den euklidischen 3-dim. Raum (allerdings in den 4-dim. Raum). D.h. Einbettungen erzeugen Artefakte, die nichts mit der "eigentlichen Mannigfaltigkeit" zu tun haben. Das spannende beim Kegel ist nicht, dass man diesen Effekt der Rotation auf die parallelverschobenen Vektoren hat – das hat man auch bei der Kugeloberfläche – sondern dass dies trotz der Flachheit des Kegels gilt. Und das spannende ist nicht, dass man diesen Effekt irgendwie mittels einer singulären Spitze erklären kann, sondern dass es ohne Spitze funktioniert.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Aruna_Gast
Gast
|
| Aruna_Gast Verfasst am: 04. Feb 2024 10:26 Titel: |
|
|
| TomS hat Folgendes geschrieben: | Dann vergiss die Unterscheidung, sie ist eher technisch.
Ohnehin wird in den meisten Darstellungen der Physiker zu viel auf Indizes herumgeritten. Wichtiger sind die Bedeutungen der koordinatenfreien Formeln. Die Indizes braucht man nur zum konkreten Rechnen, nicht für's Verständnis, was man da berechnet. Konkret: man versteht die Idee eines Kräfteparallelogramms, der Addition zweier Geschwindigkeitsvektoren oder einer Rotation sogar besser anhand von Pfeilen ohne Indizes. Das gilt auch für meine Darstellung oben, ich werde noch etwas aufräumen.
Die Idee ist, auf einer gekrümmten Fläche, das Skalarprodukt zweier Vektoren zu definieren; dies erfordert eine Verallgemeinerung
zu
D.h. das Skalarprodukt zweier Vektoren ist zunächst einfach eine lineare Abbildung g, die zwei Vektoren eine Zahl zuordnet. Speziell für y=x entspricht dies dem Quadrat des Betrages bzw. der Norm
|
Ist g hier der metrische Tensor?
| TomS hat Folgendes geschrieben: |
Hat man diese Metrik sowie die geeigneten Koordinaten inkl. deren Gültigkeitsbereichen, so ist damit eine Riemannsche Mannigfaltigkeit inkl. aller geometrischen Eigenschaften eindeutig definiert. In unserem Fall darf man sich vorstellen, dass q die punktierte euklidische Ebene deformiert:
|
die Deformation ist dann immer noch in 2D, d.h. durch g wird beschrieben, dass zwei benachbarte Punkt näher aneinander gerückt sind, oder weiter auseiander?
| TomS hat Folgendes geschrieben: |
(Mathematiker würden hier zwei sogenannte Karten einführen)
|
Steht Karte hier für Metrik?
Sind die zwei Karten dann die euklidsche Ebene einerseits und die durch g "verformte" Ebene anderseit?
| TomS hat Folgendes geschrieben: |
Warum ist das wichtig? Weil es Artefakte derartiger Einbettungen gibt! Einfachstes Beispiel ist der 2-Torus, d.h. ein an gegenüberliegenden Kanten verklebtes Rechteck. Der ist flach, d.h. verschwindende Krümmung. Was man sich aber nicht vorstellen kann, wenn man sich die Einbettung anschaut; es existiert schlicht keine überall flache Einbettung des 2-Torus in den euklidischen 3-dim. Raum
|
Meinst zu einen Zylinder?
| TomS hat Folgendes geschrieben: |
(allerdings in den 4-dim. Raum). D.h. Einbettungen erzeugen Artefakte, die nichts mit der "eigentlichen Mannigfaltigkeit" zu tun haben. Das spannende beim Kegel ist nicht, dass man diesen Effekt der Rotation auf die parallelverschobenen Vektoren hat – das hat man auch bei der Kugeloberfläche – sondern dass dies trotz der Flachheit des Kegels gilt.
|
ja, das hatte ich verstanden.
Wenn der Krümmungstensor verschwindet, sollte ein Paralletransport 0 ergeben.
Allerdings weiß ich noch nicht, wie die Paralleltransport mit dem Umlauf auf dem Kegel in Beziehung steht.
Da würde man nach meinem derzeitigen Verständnis ja erst in Richtung einer Koordinate verschieben und dann in die andere und schauen, ob bei Vertauschung der Reihenfolge eine Differenz rauskommt.
Dabei sollte auf einem flachen Kegel auch 0 rauskommen....(?)
| TomS hat Folgendes geschrieben: |
Und das spannende ist nicht, dass man diesen Effekt irgendwie mittels einer singulären Spitze erklären kann, sondern dass es ohne Spitze funktioniert. |
Ich wüsste gar nicht, wie man das mit einer Spitze erklären kann...
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18080
|
| TomS Verfasst am: 04. Feb 2024 10:34 Titel: |
|
|
Wir berechnen im folgenden den Riemannschen Krümmungstensor
auf dem Kegel. Die Arbeit reduziert sich aufgrund folgender Überlegungen:
i) im 2-dim. Raum existiert nur eine unabhängige Komponente dieses Tensors; alle andern sind entweder durch diese darstellbar, oder Null
ii) der Tensor ist antisymmetrisch im ersten Indexpaar (ab) sowie im zweiten (cd).
(ii) bedeutet, dass die Komponenten für a=b oder c=d verschwinden. Aufgrund von (i) ist es für jede 2-dim. Mannigfaltigkeit ausreichend, die Komponente (abcd) = (1212) zu berechnen.
In unserem Fall ist dies
Da g diagonal ist, und die r-Komponente gleich Eins, bleibt
Nun betrachtet man die oben berechneten Christoffel-Symbole; die meisten Indizes liefern Null.
Letztlich bleibt
Einsetzen liefert
 - (-rq^2) \frac{1}{r} = 0 )
Das ist nicht verwunderlich, wenn man sich überlegt, woher q stammt. Vergessen wir Aufschneiden und Verkleben oder Einbetten in drei Dimensionen! Wir definieren einfach eine 2-dim. Mannigfaltigkeit mit den Koordinaten
Niemand zwingt uns, mit psi und damit mit q zu arbeiten. Wir könnten auch die erste Winkelkoordinate benutzen; psi und sein Wertebereich sind lediglich gebräuchlicher.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18080
|
| TomS Verfasst am: 04. Feb 2024 11:01 Titel: |
|
|
| Aruna_Gast hat Folgendes geschrieben: | | Ist g hier der metrische Tensor? |
Jein.
g ist "die Metrik". Was tut die Metrik? Sie erlaubt die Berechnung von Skalarprodukten. Insofern ja.
Nein, wenn du dir unter dem metrischen Tensor die Darstellung als Matrix vorstellst. Die Matrix bzw. ihre Komponenten transformieren unter Koordinatentransformationen, g(x,y) nicht.
Die reale Strecke von München nach Berlin hängt nicht vom Maßstab, der Wahl des Nullmeridians oder der Kartenprojektion ab.
| Aruna_Gast hat Folgendes geschrieben: | | … die Deformation ist dann immer noch in 2D, d.h. durch g wird beschrieben, dass zwei benachbarte Punkt näher aneinander gerückt sind, oder weiter auseinander ? |
Nicht wirklich.
Schau dir den letzten Beitrag an. Die Länge eines kleinen Kreisabschnitts zwischen zwei Punkten auf einem Kreis um den Ursprung ist unabhängig von der Wahl der Koordinaten phi oder psi. Nur der Umfang dieses Kreises ändert sich.
| Aruna_Gast hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | (Mathematiker würden hier zwei sogenannte Karten einführen) |
Steht Karte hier für Metrik? |
Nein, eine Karte ist vereinfacht gesprochen ein Ausschnitt der unendlichen 2-dim. Ebene sowie eine Abbildung zwischen Mannigfaltigkeit und Ebene. Darauf kann man dann verschiedene Metriken definieren.
Die Abbildung zwischen Ausschnitt der Mannigfaltigkeit, für die die Karte gelten soll, und Ebene, ist bijektiv, d.h. invertierbar, und glatt, insbs. ohne Koordinatensingularitäten. Für Oberflächen von Kugeln, Tori, Kegeln … kann man diese Bedingung nur unter Verwendung mehrerer Karten erfüllen, die jeweils nicht die gesamte Mannigfaltigkeit abbilden. Für die zum Kegel kompaktifzierte punktierte Ebene, oder für ein zum Zylindermantel kompaktifziertes Rechteck benötigt man schon zwei Karten.
Das wird aber sehr technisch.
| Aruna_Gast hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | Warum ist das wichtig? Weil es Artefakte derartiger Einbettungen gibt! Einfachstes Beispiel ist der 2-Torus, d.h. ein an gegenüberliegenden Kanten verklebtes Rechteck. Der ist flach, d.h. verschwindende Krümmung. Was man sich aber nicht vorstellen kann, wenn man sich die Einbettung anschaut; es existiert schlicht keine überall flache Einbettung des 2-Torus in den euklidischen 3-dim. Raum
|
Meinst zu einen Zylinder? |
Nein, einen Torus.
Nimm ein Rechteck und verklebe zwei gegenüberliegende Kanten. Das liefert einen Zylindermantel. Die zwei noch nicht verklebten Kanten liefern zwei Kreise. Nun biegst du die Röhre zusammen und verklebst die Kreise.
Das liefert einen in drei Dimensionen eingebetteten Torus. Dessen Krümmung ist aber ein Artefakt dieser Einbettung.
Ich schreibe später nochwas dazu, es gibt noch eine andere, saubere und zugleich anschauliche Konstruktion für den flachen Torus.
| Aruna_Gast hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | D.h. Einbettungen erzeugen Artefakte, die nichts mit der "eigentlichen Mannigfaltigkeit" zu tun haben. Das spannende beim Kegel ist nicht, dass man diesen Effekt der Rotation auf die parallelverschobenen Vektoren hat – das hat man auch bei der Kugeloberfläche – sondern dass dies trotz der Flachheit des Kegels gilt.
|
ja, das hatte ich verstanden.
Wenn der Krümmungstensor verschwindet, sollte ein Paralletransport 0 ergeben.
Allerdings weiß ich noch nicht, wie die Paralleltransport mit dem Umlauf auf dem Kegel in Beziehung steht. |
Den Paralleltransport für den Umlauf hatte ich ja oben mittels der gekoppelten Differentialgleichungen vorgerechnet.
| Aruna_Gast hat Folgendes geschrieben: | | Da würde man nach meinem derzeitigen Verständnis ja erst in Richtung einer Koordinate verschieben und dann in die andere |
Für den Umlauf nur in psi-Richtung
| Aruna_Gast hat Folgendes geschrieben: | … und schauen, ob bei Vertauschung der Reihenfolge eine Differenz rauskommt.
Dabei sollte auf einem flachen Kegel auch 0 rauskommen....(?) |
Eben nicht.
Der Krümmungstensor folgt mittels des infinitesimalen Parallelogramms. Der Umlauf ist aber nicht infinitesimal.
Ein ähnlicher Effekt gilt für das Möbiusband: transportiere auf einem durchsichtigen Band einen Vektor, der senkrecht zur umlaufenden Linie liegt, einmal um das Möbiusband herum. Er dreht sich unterwegs nie, trotzdem hat er sich nach einem Umlauf gedreht.
Zurück zum Kegel: die Tatsache, dass R = 0 ist, der Vektor sich nach einem Umlauf dennoch gedreht hat, sagt uns, dass es sinnlos ist, irgendwo lokal nach der Ursache zu suchen.
| Aruna_Gast hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Und das spannende ist nicht, dass man diesen Effekt irgendwie mittels einer singulären Spitze erklären kann, sondern dass es ohne Spitze funktioniert. |
Ich wüsste gar nicht, wie man das mit einer Spitze erklären kann... |
Die Physiker betrachten die flache Ebene und setzen in einen Punkt eine delta-Funktion, also dort eine unendliche Krümmung.
Das ist aber Quatsch!
Schau dir nochmal die obige Argumentation an. Wir gehen aus von Koordinaten
Ich habe on meiner Rechnung aber konstanten Radius verwendet.
Betrachte also einen Kegelstumpf mit zwei offenen, kreisförmigen Rändern
Die Rechnung bleibt richtig. Eine Spitze existiert nirgendwo, nur zwei Kreisränder.
Dazu noch eine andere Konstruktion: betrachte einen endlichen, oben und unten offenen Zylindermantel; entlang (!) des Zylindermantels die Koordinate r, um den Zylinder herum die Koordinate psi. Längenmessung in r- und in psi-Richtung steckt man in die Metrik
Nun betrachte unsere Metrik auf dem endlichen, oben und unten offenen Mantel des Kegelstumpfs
Unser Fall entspricht also einem speziell deformierten Zylindermantel; die Deformation ist nur abhängig von r.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Aruna_Gast
Gast
|
| Aruna_Gast Verfasst am: 04. Feb 2024 17:41 Titel: |
|
|
| TomS hat Folgendes geschrieben: |
gilt, sowie der kovarianten Richtungsableitung
|
Ist Nabla die kovariante Richtungsableitung und A ein beliebiger Vektor?
| TomS hat Folgendes geschrieben: |
Die Forderung eines trivialen Paralleltransports führt auf
|
was bedeutet in Bezug auf Paralleltransport trivial bzw. nichttrivial?
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18080
|
| TomS Verfasst am: 04. Feb 2024 18:09 Titel: |
|
|
Zunächst mal ein paar Graphiken …
Man schaut von oben auf die Kegelspitze. Der Kegel ist dabei flach auf die Erde projiziert, der Winkel psi läuft von 0 bis 360°.
Die Abhängigkeit von den Anfangsbedingungen ist nicht so interessant.
Die Graphiken zeigen den Vektor
 = A^r(\psi) \, \hat{e}_r(\psi) + A^\psi(\psi) \, \hat{e}_\psi(\psi))
| Beschreibung: |
|
Download |
| Dateiname: |
q=0.5.png |
| Dateigröße: |
89.92 KB |
| Heruntergeladen: |
14 mal |
| Beschreibung: |
|
Download |
| Dateiname: |
q=0.9.png |
| Dateigröße: |
98.7 KB |
| Heruntergeladen: |
15 mal |
| Beschreibung: |
|
Download |
| Dateiname: |
q=1.0.png |
| Dateigröße: |
96.03 KB |
| Heruntergeladen: |
15 mal |
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 05. Feb 2024 14:04, insgesamt 2-mal bearbeitet |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18080
|
| TomS Verfasst am: 04. Feb 2024 18:22 Titel: |
|
|
| Aruna_Gast hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: |
gilt, sowie der kovarianten Richtungsableitung
|
Ist Nabla die kovariante Richtungsableitung und A ein beliebiger Vektor? |
Die kovariante Ableitung ist
Die kovariante Richtungsableitung ist dann die Projektion auf den Tangenteneinheitsvektor u der Kurve gamma
)
Der Paralleltransport von A entlang gamma ist definiert als Lösung von
| Aruna_Gast hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | Die Forderung eines trivialen Paralleltransports führt auf
|
was bedeutet in Bezug auf Paralleltransport trivial bzw. nichttrivial? |
Sorry, das muss ich natürlich erklären.
Im vorliegenden Fall bedeutet trivial, dass der Paralleltransport wegunabhängig ist.
Betrachten wir einen festen Punkt P sowie beliebige geschlossene Wege gamma von P nach P. Dann soll gelten,
"A verschoben entlang gamma = A"
In flachen Räumen gilt das sicher für Wege innerhalb bestimmter Bereiche. Auf dem Kegel gilt es immer dann, wenn die Windungszahl des Weges um die Spitze Null ist; dann ist der Transport trivial. Wenn sich die Kurve ein- oder mehrfach um die Spitze windet, dann gilt es nicht.
(Spitze nicht im wörtlichen Sinn; wir haben sie ja wegdiskutiert)
Physikalischer Sidekick – wenn's dich interessiert.
Betrachte eine lichtartige Geodäte gamma mit Tangenteneinheitsvektor u; dieser entspricht der Vierergeschwindigkeit des Photons. Der Viererimpuls ist dann proportional zu u, d.h.
Damit wird dieser gemeinsam mit u entlang von gamma parallelverschoben, d.h.
Aus diesen beiden Viererimpulsen berechnet man die gravitative oder kosmologische Rotverschiebung (die Berechnung der gemessenen Frequenz mittels "Anzahl Oszillationen pro Zeit" oder "Dehnung wg. Expansion" funktioniert nur, wenn es sich um Spezialfälle handelt; die Definition mittels Paralleltransport ist dagegen allgemeingültig)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18080
|
|
|
|
|
Registrieren
Login
FAQ
Suchen
