| Autor |
Nachricht |
Mahark
Anmeldungsdatum: 08.11.2006
Beiträge: 18
|
 Mahark Verfasst am: 08. Nov 2006 19:41 Titel: Kraftfeld aus Bewegungsgleichung Mahark Verfasst am: 08. Nov 2006 19:41 Titel: Kraftfeld aus Bewegungsgleichung |
 |
|
Wie komme ich von
einer Bewegunggleichung in Komponentenform
)
)
zu einem Vektor-Kraftfeld ) ? ?
Ich habe bereits jeweils die erste und zweite ableitung von 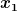 und und 
was mir bisher jedoch nicht viel nützt.
Zudem habe ich versuch 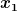 nach nach  umzustellen und in umzustellen und in  einzusetzten um so erstmal eine funktion einzusetzten um so erstmal eine funktion ) zu erhalten, zu erhalten,
jedoch bekomme ich dann \right))
hier stört mich jedoch die 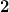 vor dem vor dem  , sonst könnte ich es mit , sonst könnte ich es mit ) = (1-x^2)^{\frac{1}{2}}) vereinfachen. vereinfachen.
Brauche dringend Hilfe!
[as_string: Ich habe mal Dein Latex etwas aufgeräumt. Ich hoffe, es war in Deinem Interesse]
|
|
 |
Patrick
Anmeldungsdatum: 05.07.2006
Beiträge: 417
Wohnort: Nieder-Wöllstadt
|
 Patrick Verfasst am: 08. Nov 2006 20:00 Titel: Patrick Verfasst am: 08. Nov 2006 20:00 Titel: |
 |
|
) = cos(arcsin(x)+arcsin(x)))
So, und jetzt benutzst du die Additionstheoreme:
 = cos(x)cos(y)-sin(x)sin(y))
Der Sinus hebt die Arcsinusfunktion auf.
sin(arcsin(x)) = x
Nach Einsetzen in die Additionstheoreme kannst du berechnen!
|
|
 |
Mahark
Anmeldungsdatum: 08.11.2006
Beiträge: 18
|
 Mahark Verfasst am: 08. Nov 2006 20:54 Titel: Mahark Verfasst am: 08. Nov 2006 20:54 Titel: |
 |
|
Vielen Dank für den Tip
damit habe ich jetzt die funktion ) bestimmt, bestimmt,
diese habe ich zweimal nach t differenziert um auf die beschleunigung zu kommen.
Jedoch habe ich noch ein Probleme ich glaube ich brauche jetzt auch die umkehrfunktion ) welche ich auch 2x ableiten muss, um zum kraftfeld zugelangen, oder gibt es da eine andere Möglichkeit? welche ich auch 2x ableiten muss, um zum kraftfeld zugelangen, oder gibt es da eine andere Möglichkeit?
Denn ich habe die Umkehrfunktion ) bestimmt und zweimal differenziert und da kamm ein übler therm raus, vorallem in vergleich zu bestimmt und zweimal differenziert und da kamm ein übler therm raus, vorallem in vergleich zu )
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 08. Nov 2006 21:10 Titel: schnudl Verfasst am: 08. Nov 2006 21:10 Titel: |
 |
|
Ein Potential mit
 = m \omega^2 \big(\frac{1}{2} x^2 + 2y^2 \big) )
ergibt eine Bewegungsgleichung, die als spezielle Lösung Deine angegebene enthält. Es mag aber andere Potentialformen geben, die zur gleichen partikulären Lösung kommen.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
Mahark
Anmeldungsdatum: 08.11.2006
Beiträge: 18
|
 Mahark Verfasst am: 08. Nov 2006 21:22 Titel: Mahark Verfasst am: 08. Nov 2006 21:22 Titel: |
 |
|
|
Wenn du mir zeigen könntest wie ich über das kraftfeld auf dieses potential komme wäre das perfekt, allerdings habe ich den gradienten des potentials gebildet und das kraftfeld sieht anders aus als das was ich berechnet habe die y-komponente ist 4b / a^2
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 08. Nov 2006 21:40 Titel: schnudl Verfasst am: 08. Nov 2006 21:40 Titel: |
 |
|
Naja:
Die Lagrangefunktion ist

Die Bewegungsgleichung ist:

und

Das ergibt

und

Die Lösung der ersten Gleichung (für x) ist:
 = A_x \sin(\omega t) + B_x \cos (\omega t))
Die Lösung der zweiten Gleichung (für y) ist:
 = A_y \sin(2 \omega t) + B_y \cos (2 \omega t))
Bei Deiner speziellen Lösung ist




Diese ist somit ein Spezialfall der allgemeinen Lösung mit ganz bestimmten Anfangsbedingungen.
Das Kraftfeld ist dann der Gradient aus dem Potential und somit

und

_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe)
Zuletzt bearbeitet von schnudl am 09. Nov 2006 14:59, insgesamt einmal bearbeitet |
|
 |
Mahark
Anmeldungsdatum: 08.11.2006
Beiträge: 18
|
 Mahark Verfasst am: 08. Nov 2006 22:47 Titel: Mahark Verfasst am: 08. Nov 2006 22:47 Titel: |
 |
|
Das sieht ganz gut aus aber ich verstehe nicht wie ich von dem kraftfeld auf die bewegungsgleichung (mit sin und cos) komme. wenn ich aus dem kraftfeld das "beschleunigungsfeld" erstelle (durch m dividieren)
dann müsste ich doch durch zweimaliges intigrieren auf die bewegungsgleichung kommen, doch da komm ich nicht drauf wie kommt denn der sinus und cosinus darein
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 09. Nov 2006 07:48 Titel: schnudl Verfasst am: 09. Nov 2006 07:48 Titel: |
 |
|
Da verstehe ich Deine Vorgangsweise nicht ...
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
 isi1 Verfasst am: 09. Nov 2006 11:41 Titel: Re: Kraftfeld aus Bewegungsgleichung isi1 Verfasst am: 09. Nov 2006 11:41 Titel: Re: Kraftfeld aus Bewegungsgleichung |
 |
|
| Mahark hat Folgendes geschrieben: |
)
) |
Hallo Mahark,
so beindruckend auch schnudls Ableitung ist, ich verstehe doch noch nicht alles. Sollte nicht  sein? sein?
Und war nicht Lagrange der Typ, der damit prahlte, in seinem Buch keine einzige Zeichnung benötigt zu haben?
Für mich sind Deine Ausgangsgleichungen eine Lissajous-Figur:
 http://www2.filehost.to/files/2006-11-09_02/113312_Lissajou2.JPG http://www2.filehost.to/files/2006-11-09_02/113312_Lissajou2.JPG
z.B. erzeugt durch ein Pendel in einem Kraftfeld mit schnudls Komponenten (in x2-Richtung eine größere Rückstellkraft wie in x1-Richtung).
Edit: siehe unten bei schnudl?
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ
Zuletzt bearbeitet von isi1 am 09. Nov 2006 16:42, insgesamt 2-mal bearbeitet |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 09. Nov 2006 14:57 Titel: schnudl Verfasst am: 09. Nov 2006 14:57 Titel: |
 |
|
Meiner Ansicht nach kann man zu einer vorgegebenen Bewegung nicht das zugehörige Potential finden.
z.B. sieht eine kreisförmige Planetenbewegung im 1/r Potential so aus:
 = R \sin (\omega t))
 = R \cos (\omega t))
Dies könnte aber ebenso die Bewegung in einem beliebig anderen(radialsymmetrischen) Potential sein. Die kinetische Energie ist ja konstant und die Trajektorie ist eine Äquipotentiallinie. Eine solche gibt es aber bei jedem radialsymmetrischen Potential !
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
 isi1 Verfasst am: 09. Nov 2006 16:34 Titel: isi1 Verfasst am: 09. Nov 2006 16:34 Titel: |
 |
|
| schnudl hat Folgendes geschrieben: | | Meiner Ansicht nach kann man zu einer vorgegebenen Bewegung nicht das zugehörige Potential finden. |
Hallo schnudl,
jetzt hast Du mich dazu gebracht, an meinen obigen Bemerkungen zu zweifeln. Was Du da anführst stimmt zwar für die Kreisbewegung, aber nicht für die oben gezeichnete Lissajous-Figur. Da der Cos(2wt) dazu führt, dass die Masse durch das Zentrum läuft, wird z.B. im 1/r²-Feld die Geschwindigkeit viel größer werden. Maharks Ausgangsgleichungen sind dann nicht mehr erfüllt (glaube ich wenigstens).
Du weißt das sicher auf Anhieb.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 10. Nov 2006 07:20 Titel: schnudl Verfasst am: 10. Nov 2006 07:20 Titel: |
 |
|
@isi
Ich denke du hast die falsche Formel geplottet. Bei mir sieht die Kurve ganz anders aus. Ich bekomme Deine Kurve, wenn ich beide male sinus statt einmal sinus und einmal cosinus nehme. Die Kurve geht dann bei mir nicht durch den Nullpunkt.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
 isi1 Verfasst am: 10. Nov 2006 07:23 Titel: isi1 Verfasst am: 10. Nov 2006 07:23 Titel: |
 |
|
| schnudl hat Folgendes geschrieben: | @isi
Ich denke du hast die falsche Formel geplottet. Bei mir sieht die Kurve ganz anders aus. Ich bekomme Deine Kurve, wenn ich beide male sinus statt einmal sinus und einmal cosinus nehme. Die Kurve geht dann bei mir nicht durch den Nullpunkt. |
Guten Morgen schnudl, könntest Du den Graphen bitte zeigen?
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 10. Nov 2006 07:29 Titel: schnudl Verfasst am: 10. Nov 2006 07:29 Titel: |
 |
|
muss jetzt frühstück für die kinder kochen - daher nur das excel
| Beschreibung: |
|

Download |
| Dateiname: |
Mappe1.xls |
| Dateigröße: |
57 KB |
| Heruntergeladen: |
205 mal |
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
 isi1 Verfasst am: 10. Nov 2006 08:25 Titel: isi1 Verfasst am: 10. Nov 2006 08:25 Titel: |
 |
|
Ja, stimmt, Schnudl,
ich hatte die eine Frequenz geringfügig erhöht, damit sich die Figur dreht und in einer falschen Phase das Foto gemacht. Das für die phasenverschobene Kurve nötige Potential ist m.E. immer noch das von Dir berechnete (in einer Richtung ist die Rückstellkraft 4*w²*xi, in der anderen w²*xj --- z.B. ein federndes Flacheisen, das hochkant vier mal soviel Kraft ausübt wie flachkant)
Das Argument bleibt gleich: die Kurve ist nicht radial symmetrisch, die Bahngeschwindigkeit nicht konstant.
Diskussion: Satz: Im 1/r²-Feld gibt es nur Kegelschnitte als Trägheitsbahnen.
Behauptung: Die Lissajous-Figur ist kein Kegelschnitt <--> Sie kann nicht im 1/r²-Feld entstehen.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 10. Nov 2006 09:24 Titel: schnudl Verfasst am: 10. Nov 2006 09:24 Titel: |
 |
|
| isi1 hat Folgendes geschrieben: | Ja, stimmt, Schnudl,
ich hatte die eine Frequenz geringfügig erhöht, damit sich die Figur dreht und in einer falschen Phase das Foto gemacht. Das für die phasenverschobene Kurve nötige Potential ist m.E. immer noch das von Dir berechnete (in einer Richtung ist die Rückstellkraft 4*w²*xi, in der anderen w²*xj --- z.B. ein federndes Flacheisen, das hochkant vier mal soviel Kraft ausübt wie flachkant)
Das Argument bleibt gleich: die Kurve ist nicht radial symmetrisch, die Bahngeschwindigkeit nicht konstant.
Diskussion: Satz: Im 1/r²-Feld gibt es nur Kegelschnitte als Trägheitsbahnen.
Behauptung: Die Lissajous-Figur ist kein Kegelschnitt <--> Sie kann nicht im 1/r²-Feld entstehen. |
Das mit dem 1/r Potential habe ich ja nicht 1:1 übertragen auf das vorliegende problem. Ich wollte damit nur zeigen, dass es durchaus viele verschiedene Potentiele geben kann, die zu einer gleichen Bewegung Anlass geben können.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
 isi1 Verfasst am: 10. Nov 2006 09:27 Titel: isi1 Verfasst am: 10. Nov 2006 09:27 Titel: |
 |
|
Alles klar, Schnudl 
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
|

















