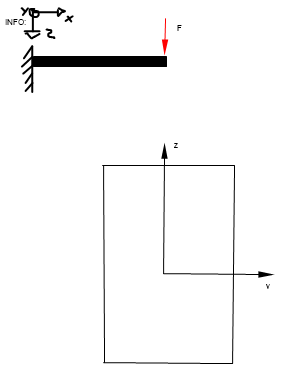
Axiales Flächenträgheitsmoment 2. Grades

haraldo · Anmeldungsdatum: 02.10.2022 Beiträge: 2

Moin,

Bei den axialen Flächenträgheitsmoment weiß ich, dass ich Iy berechnen muss, da das Teil mit einer Querkraft oder einfach gesagt, auf der z - Achse beansprucht wird.

Aber das reicht nicht als Erklärung, vll kennt sich ja jemand damit aus.

Mathefix · Anmeldungsdatum: 05.08.2015 Beiträge: 5867 Wohnort: jwd

Welche Erklärung erwartest Du?
Möchtest Du wissen warum das Flächenträgheitsmoment erforderlich ist?

haraldo · Anmeldungsdatum: 02.10.2022 Beiträge: 2

Moin,

Ich bräuchte eine Erklärung um es zu verstehen, wie das axiale Flächenträgheits- und Widerstandsmomente aufgebaut sind und was die miteinander zutun haben.

hansguckindieluft · Anmeldungsdatum: 23.12.2014 Beiträge: 1212

schau Dir diesen Thread mal an. Da wurde das Thema recht umfangreich besprochen:
https://www.techniker-forum.de/thema/flaechentraegheitsmoment-und-achsen.97209/

Mathefix · Anmeldungsdatum: 05.08.2015 Beiträge: 5867 Wohnort: jwd

Um die Zusammenhänge zu verstehen, muss man etwas weiter ausholen.

Annahmen:
1. Der Querschnitt im Balken bleibt eben; keine Verwerfungen
2. Es gilt das Hooke'sche Gesetz: Dehnung und Spannung sind proportional.

Das Biegemoment biegt den Balken nach unten durch und ruft im Balkenquerschnitt Normalspannungen hervor.
Die obere Randfaser des Balkens wird um

gedehnt, die unteren um

verkürzt. Im Querschnitt beträgt die Längenänderung der Fasern

Hooke'sche Gesetz

e = Abstand der neutralen Faser vom Rand

Gleichbewichtsbedingung

Die Summe der Zug- und Druckkräfte im Querschnitt müssen sich aufheben:

dA = Querschnittselement

Das besagt, das die Querschnittsachse in der weder Zug- noch Druckspannung herrscht die neutrale Faser ist, die durch den Schwerpunkt der Querschnittsfläche geht, also die 2. Hauptachse des Querschnitts ist.

Auf diese Achse bezogen, ergeben die Spannungen mit ihren zugehörigen Flächenelementen multipliziert ein Moment.

Mit

ist das axiale Trägheitsmoment I

ist das Widerstandsmoment W

Damit ist

roycy · Anmeldungsdatum: 05.05.2021 Beiträge: 961