| Autor |
Nachricht |
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18049
|
 TomS Verfasst am: 10. Jul 2022 13:23 Titel: |
 |
|
Hör doch bitte auf, Dinge auseinanderzudividieren, die ich zusammenfasse.
Die Menge der natürlichen Zahlen mit den Peano-Axiomen ist eine mathematische Struktur (ja, auch ohne, aber das interessiert mich nicht). Und wenn die Peano-Axiomen inkonsistent sind, dann auch die mathematische Struktur „Menge der natürlichen Zahlen mit den Peano-Axiomen“.
Um mehr geht es nicht.
| index_razor hat Folgendes geschrieben: | | Kannst du mal genau erläutern was du unter einer Inkonsistenz verstehst und was eine inkonsistente Struktur sein soll? |
Zum Beispiel die Menge der natürlichen Zahlen mit einem inkonsistenten Axiomensystem (welches auch immer).
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 10. Jul 2022 13:30 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | Hör doch bitte auf, Dinge auseinanderzudividieren, die ich zusammenfasse: |
Ich versuche nur Dinge auseinanderzuhalten, die nicht zusammengehören, nämlich Strukturen und Aussagen/Theorien. Das war genau das Problem mit deiner Aussage über "konsistente Strukturen".
Und das Problem besteht anscheinend immer noch:
| Zitat: | | Und wenn die Peano-Axiomen inkonsistent sind, dann auch die mathematische Struktur „Menge der natürlichen Zahlen mit den Peano-Axiomen“. |
Nun gut, ich glaube dazu ist alles gesagt.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18049
|
| TomS Verfasst am: 10. Jul 2022 13:41 Titel: |
|
|
Ich verstehe‘s nicht.
Tegmark spricht von „self-consistent mathematical structures“ und ich habe dir erklärt, was ich darunter verstehe - bzw. unter dem Gegenteil.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 10. Jul 2022 14:01 Titel: |
|
|
| TomS hat Folgendes geschrieben: | Ich verstehe‘s nicht.
Tegmark spricht von „self-consistent mathematical structures“
|
Wo denn? Es widerspricht seiner Verwendung des Begriffs "mathematical structure" aus dem MUH-paper. Selbstkonsistenz ist eine Eigenschaft von Mengen von Aussagen, nicht von Strukturen.
| Zitat: |
und ich habe dir erklärt, was ich darunter verstehe - bzw. unter dem Gegenteil. |
Ich weiß was die natürlichen Zahlen sind (eine Struktur), und ich weiß was die Peano-Axiome sind (keine Struktur, sondern eine Menge von Aussagen). Ich habe aber keine Ahnung was für eine Struktur „die Menge der natürlichen Zahlen mit den Peano-Axiomen“ sein soll.
Die Frage nach der Konsistenz der Peano-Axiome ist sinnvoll. Die Frage nach der Konsistenz der natürlichen Zahlen ist sinnlos.
P.S. Ich frage mich ob es was bringt, in Zukunft bei ähnlichen Diskussionen einfach auf diesen Blogpost zu verweisen. In der Kommentarsektion spielt sich sogar praktisch dieselbe Diskussion ab wie hier.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
|
Haudegen007
Gast
|
| Haudegen007 Verfasst am: 10. Jul 2022 17:17 Titel: |
|
|
|
Also auch hier: Einigkeit über Uneinigkeit;) |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18049
|
| TomS Verfasst am: 10. Jul 2022 20:57 Titel: |
|
|
| index_razor hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | Ich verstehe‘s nicht.
Tegmark spricht von „self-consistent mathematical structures“
|
Wo denn? |
Hier (und in seinem Buch)
https://arxiv.org/pdf/0704.0646.pdf
| Zitat: | Bearing these correspondences in mind, let us now discuss the Gödel-inspired worry mentioned above: that the MUH makes no sense because our universe would be somehow inconsistent or undefined. If one accepts David Hilbert’s dictum that “mathematical existence is merely freedom from contradiction” [126], then an inconsistent structure would not exist mathematically, let alone physically as in the MUH.
Our standard model of physics includes everyday mathematical structures such as the integers (defined by the Peano axioms) and real numbers. |
| index_razor hat Folgendes geschrieben: | | Die Frage nach der Konsistenz der Peano-Axiome ist sinnvoll. Die Frage nach der Konsistenz der natürlichen Zahlen ist sinnlos. |
S.o.:
| Zitat: | | Our standard model of physics includes everyday mathematical structures such as the integers (defined by the Peano axioms). |
Das Problem ist, dass du die Struktur = “Menge plus Relationen auf der Memge” in die Einzelbestandteile trennen möchtest. Aber das ist natürlich sinnlos, und Tegmark tut dies auch nicht. Beides zusammen ergibt die Struktur, und damit auch deren Konsistenz.
| index_razor hat Folgendes geschrieben: | | Ich weiß was die natürlichen Zahlen sind (eine Struktur), und ich weiß was die Peano-Axiome sind (keine Struktur, sondern eine Menge von Aussagen). Ich habe aber keine Ahnung was für eine Struktur „die Menge der natürlichen Zahlen mit den Peano-Axiomen“ sein soll. |
Umgekehrt wüsste ich nicht, dass irgendeine Definition der natürlichen Zahlen ohne die Peano-Axiome oder ein anderes äquivalentes Axiomensystem existiert.
Kennst du eine?
Ich weiß nicht, welches Problem du damit hast, eine mathematische Struktur als Menge plus Axiome, Relationen o.ä. aufzufassen. Ich finde kein Beispiel, das irgendwie nahelegt, dass keine Relationen, Axiome o.ä. notwendig wären.
https://de.m.wikipedia.org/wiki/Mathematische_Struktur
| Zitat: | | Eine mathematische Struktur ist eine Menge mit bestimmten Eigenschaften. Diese Eigenschaften ergeben sich durch eine oder mehrere Relationen zwischen den Elementen … Diese Relationen und damit auch die Struktur, die sie definieren, können von sehr verschiedener Art sein. Eine solche Art lässt sich durch gewisse Axiome festlegen, die die definierenden Relationen zu erfüllen haben. |
und viele Beispiele im Folgenden.
Tegmark erklärt das im Anhang A.
Tegmark erklärt in dem Paper auch, inwiefern Identität vorliegt:
| Zitat: | | Whereas the customary terminology in physics textbooks is that the ex- ternal reality is described by mathematics, the MUH states that it[the external reality] is mathematics (more specifically, a mathematical structure). This corresponds to the “ontic” version of universal structural realism in the philosophical terminology of [14, 22]. If a future physics textbook contains the TOE, then its equations are the complete description of the mathematical structure that is the external physical reality. We write is rather than corresponds to here, because if two structures are isomorphic, then there is no meaningful sense in which they are not one and the same [19]. From the definition of a mathematical structure (see Appendix A), it follows that if there is an isomorphism between a mathematical structure and another structure (a one-to-one correspondence between the two that respects the relations), then they are one and the same. If our external physical reality is isomorphic to a mathematical structure, it therefore fits the definition of being a mathematical structure. |
Es steht m.E. alles glasklar da.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 10. Jul 2022 22:15 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | Ich verstehe‘s nicht.
Tegmark spricht von „self-consistent mathematical structures“
|
Wo denn? |
Hier (und in seinem Buch)
https://arxiv.org/pdf/0704.0646.pdf
Bearing these correspondences in mind, let us now discuss the Gödel-inspired worry mentioned above: that the MUH makes no sense because our universe would be somehow inconsistent or undefined. If one accepts David Hilbert’s dictum that “mathematical existence is merely freedom from contradiction” [126], then an inconsistent structure would not exist mathematically, let alone physically as in the MUH.
Our standard model of physics includes everyday mathematical structures such as the integers (defined by the Peano axioms) and real numbers. |
Danke.
Kannst du definieren was die Phrase "inkonsistente Struktur" bedeutet oder mir sagen ob Tegmark sie irgendwo definiert? [EDIT: hat sich, glaube ich, schon erledigt, siehe nächster Beitrag] Kann dich vielleicht der oben verlinkte Blogpost (sowie die dortige Diskussion) davon überzeugen, daß dies Unsinn ist? All dies sind Grundbegriffe der mathematischen Logik. Da kann es nicht viel Spielraum für verschiedene Ansichten geben. Vielleicht hilft es auch wenn wir versuchen die Begriffe "Konsistenz" und "mathematische Struktur" etwas genauer definieren? (siehe unten)
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Die Frage nach der Konsistenz der Peano-Axiome ist sinnvoll. Die Frage nach der Konsistenz der natürlichen Zahlen ist sinnlos. |
s.o.: Our standard model of physics includes everyday mathematical structures such as the integers (defined by the Peano axioms).
|
Ich sehe zwar nicht den Zusammenhang zu meiner Aussage. Aber das ist der nächste Schnitzer. Die natürlichen Zahlen werden nicht durch die Peano-Axiome (oder irgendwelche anderen Axiome) definiert. Das folgt aus der Existenz von Nichtstandardmodellen der Arithmetik, die alle Peano-Axiome erfüllen, aber nicht isomorph zu den natürlichen Zahlen sind. Es folgt auch aus den Gödelschen Unvollständigkeitssätzen: es gibt Aussagen, die auf die natürlichen Zahlen zutreffen, aber nicht aus den Peano-Axiomen folgen.
| Zitat: |
Ich weiß immer noch nicht, welches Problem du damit hast, eine mathematische Struktur als Menge plus Axiomen, Relationen o.ä. aufzufassen. |
Ungefähr dasselbe Problem, das ich damit habe, den Mars als "Planet des Sonnensystems plus Keplersche Gesetze" aufzufassen. Der Mars ist ein Planet und die Keplerschen Gesetze sind Aussagen über diesen Planet--zwei vollkommen verschiedene Dinge.
Analog: Die Menge der Natürlichen Zahlen plus der Nachfolgeoperation (eine Relation) ist eine mathematische Struktur. Die Peano-Axiome sind Aussagen über diese Struktur.
Allgemein: eine Struktur ist eine Menge plus Relationen. Axiome sind Aussagen in einer formalen Sprache. Eine Struktur ist also mehr als eine Menge, aber nicht eine Menge plus irgendwelche Axiome.
Der Zusammenhang zwischen Axiomen und Strukturen besteht vielmehr in der Interpretation der Axiome. Eine Struktur ist ein Modell für eine Menge von Axiomen, wenn jedes Axiom wahr wird, sofern es als Aussage über die Menge interpretiert wird.
Eine Menge P von Aussagen ist konsistent, wenn es nicht möglich ist sowohl eine Aussage p als auch die Negation ~p aus P formal abzuleiten. P ist inkonsistent, wenn P nicht konsistent ist. Ist klar, daß diese Definition nicht den geringsten Sinn in Bezug auf Strukturen wie 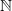 ergibt? Es handelt sich um rein syntaktische Begriffe. Sie haben absolut nichts mit der Bedeutung der Aussagen in P zu tun.
Man kann aber folgendes sagen: 1) Jede konsistente Menge von Axiomen besitzt ein Modell (eine Folge des Gödelschen Vollständigkeitssatzes).
2) Eine inkonsistente Menge von Axiomen besitzt kein Modell. Das ist im Prinzip sofort klar, da es keine Interpretation geben kann, mit der sowohl p als auch ~p wahr wird.
Das ist der Zusammenhang zwischen der Konsistenz eines Axiomensystems und der Existenz einer Struktur. Du (und Tegmark) verballhornst das zur "Konsistenz einer Struktur" und bringst damit zwei vollkommen verschiedene Dinge durcheinander.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt
Zuletzt bearbeitet von index_razor am 10. Jul 2022 22:45, insgesamt 4-mal bearbeitet |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 10. Jul 2022 22:29 Titel: |
|
|
Ergänzung:
| TomS hat Folgendes geschrieben: |
Das Problem ist, dass du die Struktur = “Menge plus Relationen auf der Memge” in die Einzelbestandteile trennen möchtest.
|
Nein, das hast du falsch verstanden. Menge plus Relationen ist ok. Das will ich nicht trennen. (Das war sogar meine ursprüngliche Definition.) Aber eine Menge plus Relationen kann nicht konsistent oder inkonsistent sein, nur Aussagen können das sein.
| Zitat: |
Umgekehrt wüsste ich nicht, dass irgendeine Definition der natürlichen Zahlen ohne die Peano-Axiome oder ein anderes äquivalentes Axiomensystem existiert.
Kennst du eine?
|
Es gibt keine und es kann keine geben, nicht mit den Peano- oder äquivalenten Axiomen oder ohne. Es gibt verschiedene Charakterisierungen der natürlichen Zahlen innerhalb von Modellen der Mengenlehre. (Ungefähr sowas wie "kleinste induktive Menge" etc.)
| Zitat: |
https://de.m.wikipedia.org/wiki/Mathematische_Struktur
| Zitat: | | Eine mathematische Struktur ist eine Menge mit bestimmten Eigenschaften. Diese Eigenschaften ergeben sich durch eine oder mehrere Relationen zwischen den Elementen … Diese Relationen und damit auch die Struktur, die sie definieren, können von sehr verschiedener Art sein. Eine solche Art lässt sich durch gewisse Axiome festlegen, die die definierenden Relationen zu erfüllen haben. |
und viele Beispiele im Folgenden.
Tegmark erklärt das im Anhang A.
|
Aus der Definition im Anhang A.1 geht m.E. klar hervor, daß er 1) Axiome nicht als Teil der Struktur ansieht und daß 2) es sinnlos ist von einer konsistenten Struktur zu reden. Ich vermute ihm ist im Text einfach ein Patzer unterlaufen.
| Zitat: |
Tegmark erklärt in dem Paper auch, inwiefern Identität vorliegt:
|
Ich habe auch keine Einwände gegen die Behauptung der MUH selbst. Ich hatte nur ein Problem mit der Aussage "Eine Struktur existiert genau dann, wenn sie konsistent ist", da sie sinnlos ist.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18049
|
| TomS Verfasst am: 11. Jul 2022 06:50 Titel: |
|
|
Ich weiß nicht, wieviele Zitate du noch sehen möchtest.
https://de.m.wikipedia.org/wiki/Mathematische_Struktur
| Zitat: | Eine mathematische Struktur ist eine Menge mit bestimmten Eigenschaften. Diese Eigenschaften ergeben sich durch eine oder mehrere Relationen zwischen den Elementen … Diese Relationen und damit auch die Struktur, die sie definieren, können von sehr verschiedener Art sein. Eine solche Art lässt sich durch gewisse Axiome festlegen, die die definierenden Relationen zu erfüllen haben. Die wichtigsten großen Typen, in die sich Strukturen klassifizieren lassen, sind algebraische Strukturen …
Eine algebraische Struktur … ist eine Struktur … die nur durch eine oder mehrere Verknüpfungen definiert ist (als Funktionen sind Verknüpfungen spezielle Relationen) …
Zahlbereiche sind die Mengen, mit denen man gewöhnlich rechnet. Grundlage ist die Menge der natürlichen Zahlen. Als algebraische Verknüpfung dienen Addition und Multiplikation … |
https://de.m.wikipedia.org/wiki/Natürliche_Zahl
| Zitat: | | Richard Dedekind definierte 1888 erstmals die natürlichen Zahlen implizit durch Axiome.[2] Unabhängig von ihm stellte Giuseppe Peano 1889 ein einfacheres und zugleich formal präzises Axiomensystem auf … Andere Axiomatisierungen der natürlichen Zahlen, die mit der Peano-Arithmetik verwandt sind, sind beispielsweise die Robinson-Arithmetik und die primitiv rekursive Arithmetik … Man kann die Peano-Axiome auch als Definition der natürlichen Zahlen auffassen. Eine Menge der natürlichen Zahlen ist dann eine solche Menge, die den Peano-Axiomen genügt. Wichtig ist, dass es unendlich viele solcher Mengen gibt. Jedoch verhält sich jede dieser Mengen völlig gleich, die Elemente sind lediglich anders bezeichnet. In der Mathematik sagt man, die Mengen sind isomorph. Dieses Resultat nennt man auch den Eindeutigkeitssatz von Dedekind. |
Wenn also eine mathematische Struktur einer Menge plus Relationen entsprechen, und wenn diese Relationen durch Axiome festgelegt oder zumindest eingegrenzt werden, dann überträgt sich die Konsistenz (oder Inkonsistenz) auch auf die Struktur.
Wenn man “die Peano-Axiome als Definition der natürlichen Zahlen auffassen” kann, dann folgt die Konsistenz (oder Inkonsistenz) der natürlichen Zahlen auch aus der Konsistenz (oder Inkonsistenz) der Peano-Axiome.
Dass du Axiome nicht betrachten möchtest, steht also im Widerspruch zu dem, was andere dazu schreiben.
Was eine “konsistente mathematische Struktur” ist, sollte dann offensichtlich sein: eine Struktur, für die bzw. in der mittels der Relationen bzw. Axiome keine Widersprüche folgen. Die Bedeutung von “inkonsistente mathematische Struktur” ist wohl so offensichtlich, dass Tegmark (oder jemanden anders) sie nicht explizit erwähnt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 11. Jul 2022 08:07, insgesamt einmal bearbeitet |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 11. Jul 2022 07:50 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | Ich weiß nicht, wieviele Zitate du noch sehen möchtest. |
Ich will nicht noch mehr irrelevante Zitate sehen, sondern daß du dich mit den Tatsachen auseinandersetzt. Falls das zu viel verlangt ist, können wir das hier natürlich bleiben lassen.
Ich habe keine Ahnung warum du mir dauernd die Definition von mathematischen Strukturen vorhältst. Ich weiß was das ist. Niemand außer dir, auch nicht Tegmark, definiert eine mathematische Struktur als "Menge plus Relationen plus Axiome". Und nach Tegmarks Definition aus Anhang A.1 ist deine These "eine mathematische Struktur existiert dann und nur dann, wenn sie konsistent ist" Unsinn.
Deine Behauptung "eine mathematische Struktur existiert dann und nur dann, wenn sie konsistent ist", hat nichts mit natürlichen Zahlen zu tun. Selbst wenn es wahr wäre, daß die Peano-Arithmetik natürliche Zahlen "definieren" würde, wäre die Behauptung immer noch Unsinn.
Einige der wichtigsten Stellen aus dem Abschnitt hast du weggelassen. (Er ist aber trotzdem nicht sehr gut.)
"Während sich das ursprüngliche Axiomensystem in Prädikatenlogik zweiter Stufe formalisieren lässt, wird heute oft eine schwächere Variante in Prädikatenlogik erster Stufe verwendet, die als Peano-Arithmetik bezeichnet wird.
[...]
Man kann die Peano-Axiome auch als Definition der natürlichen Zahlen auffassen. Eine Menge der natürlichen Zahlen ist dann eine solche Menge, die den Peano-Axiomen genügt. Wichtig ist, dass es unendlich viele solcher Mengen gibt. Jedoch verhält sich jede dieser Mengen völlig gleich, die Elemente sind lediglich anders bezeichnet. In der Mathematik sagt man, die Mengen sind isomorph.
Der letzte Absatz gilt nur in der Logik zweiter Stufe. Das hilft aber m.E. in dieser Diskussion nicht weiter. Denn es gilt z.B. kein zum Vollständigkeitssatz analoges Resultat in der Logik zweiter Stufe und der Zusammenhang zwischen Konsistenz der Axiome und der Existenz eines Modells, m.a.W. der Kern des Arguments, bricht zusammen. Die ganze Idee stammt aus der Logik erster Stufe.
| Zitat: |
Man kann die Peano-Axiome auch als Definition der natürlichen Zahlen auffassen. Eine Menge der natürlichen Zahlen ist dann eine solche Menge, die den Peano-Axiomen genügt. Wichtig ist, dass es unendlich viele solcher Mengen gibt. Jedoch verhält sich jede dieser Mengen völlig gleich, die Elemente sind lediglich anders bezeichnet. In der Mathematik sagt man, die Mengen sind isomorph. Dieses Resultat nennt man auch den Eindeutigkeitssatz von Dedekind. |
Das bezieht sich auf die Logik zweiter Stufe und ist damit für diese Diskussion irrelevant. Und in der Logik erster Stufe ist es vollkommen falsch. Überabzählbare nichtstandard-Modelle der Peano-Arithmetik -- und um keine anderen Axiome geht es hier -- sind selbstverständlich nicht isomorph zu den natürlichen Zahlen und verhalten sich absolut nicht so. Außerdem gilt dort für Axiomensysteme der Arithmetik der Gödelsche Unvollständigkeitssatz.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 11. Jul 2022 08:00 Titel: |
|
|
| TomS hat Folgendes geschrieben: | Wenn also eine mathematische Struktur einer Menge plus Relationen entsprechen, und wenn diese Relationen durch Axiome festgelegt oder zumindest eingegrenzt werden, dann überträgt sich die Konsistenz (oder Inkonsistenz) auch auf die Struktur.
Wenn man “die Peano-Axiome als Definition der natürlichen Zahlen auffassen” kann, dann folgt die Konsistenz (oder Inkonsistenz) der natürlichen Zahlen auch aus der Konsistenz (oder Inkonsistenz) der Peano-Axiome.
|
Meine Güte. Konsistenz eines Axiomensystems bedeutet, daß man nicht sowohl eine Aussage als auch ihre Negation formal aus den Axiomen beweisen kann. Diese Eigenschaft "überträgt" sich nicht auf Strukturen. Es ist nämlich Nonsens davon zu reden, z.B. eine arithmetische Aussage aus einer Menge von Zahlen zu beweisen.
Stattdessen folgt aus der Konsistenz von Axiomen, die Existenz einer Struktur, die alle Axiome erfüllt (mittels eines einfachen, aber nicht ganz trivialen Arguments). Ist das so schwer?
| Zitat: |
Dass du Axiome nicht betrachten möchtest, steht also im Widerspruch zu dem, was andere dazu schreiben. |
Du hast mich mißverstanden.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18049
|
| TomS Verfasst am: 11. Jul 2022 08:21 Titel: |
|
|
| index_razor hat Folgendes geschrieben: | | Niemand außer dir, auch nicht Tegmark, definiert eine mathematische Struktur als "Menge plus Relationen plus Axiome". |
Ein Strohmann? Das habe ich so nicht zitiert oder geschrieben.
| index_razor hat Folgendes geschrieben: | | Und nach Tegmarks Definition aus Anhang A.1 ist deine These "eine mathematische Struktur existiert dann und nur dann, wenn sie konsistent ist" Unsinn. |
Könntest du das bitte konkret zitieren?
| index_razor hat Folgendes geschrieben: | Einige der wichtigsten Stellen aus dem Abschnitt hast du weggelassen. (Er ist aber trotzdem nicht sehr gut.)
[i]"Während sich das ursprüngliche Axiomensystem in Prädikatenlogik zweiter Stufe formalisieren lässt, wird heute oft eine schwächere Variante in Prädikatenlogik erster Stufe verwendet, die als Peano-Arithmetik bezeichnet wird. |
Das habe ich nicht vergessen, das ist mit durchaus bewusst; ging um ein Beispiel.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 11. Jul 2022 08:34 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Niemand außer dir, auch nicht Tegmark, definiert eine mathematische Struktur als "Menge plus Relationen plus Axiome". |
Ein Strohmann? Das habe ich so nicht zitiert oder geschrieben.
|
Doch hier
| TomS hat Folgendes geschrieben: | | Ich weiß nicht, welches Problem du damit hast, eine mathematische Struktur als Menge plus Axiome, Relationen o.ä. aufzufassen. Ich finde kein Beispiel, das irgendwie nahelegt, dass keine Relationen, Axiome o.ä. notwendig wären. |
Die Axiome sind hier das einzige worauf sich überhaupt der Begriff "Konsistenz" anwenden läßt. Und sie haben als einzige in dieser Aufzählung nichts zu suchen.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Und nach Tegmarks Definition aus Anhang A.1 ist deine These "eine mathematische Struktur existiert dann und nur dann, wenn sie konsistent ist" Unsinn. |
Könntest du das bitte konkret zitieren?
|
In dem Anhang werden, sofern mir nichts entgangen ist, Axiome nicht in der Definition einer Struktur erwähnt, also nichts worauf sich der Begriff "Konsistenz" anwenden ließe.
| Zitat: |
| index_razor hat Folgendes geschrieben: | Einige der wichtigsten Stellen aus dem Abschnitt hast du weggelassen. (Er ist aber trotzdem nicht sehr gut.)
[i]"Während sich das ursprüngliche Axiomensystem in Prädikatenlogik zweiter Stufe formalisieren lässt, wird heute oft eine schwächere Variante in Prädikatenlogik erster Stufe verwendet, die als Peano-Arithmetik bezeichnet wird. |
Das habe ich nicht vergessen, das ist mit durchaus bewusst; ging um ein Beispiel. |
Wenn dein Beispiel Logik zweiter Stufe erfordert, ist es für die MUH m.E. irrelevant. Außerdem müßtest du es nicht für ein Axiomensystem zeigen, sondern für alle.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18049
|
| TomS Verfasst am: 11. Jul 2022 09:34 Titel: |
|
|
Mein zitierter Text enthält kein zweifaches “und”. Den Zusammenhang zwischen Relationen und Axiomen habe ich oben genannt.
Mir schleierhaft, wie du auf die Idee kommst ...
| index_razor hat Folgendes geschrieben: | | Die Axiome sind hier das einzige worauf sich überhaupt der Begriff "Konsistenz" anwenden läßt. Und sie haben als einzige in dieser Aufzählung nichts zu suchen. |
| index_razor hat Folgendes geschrieben: | | In dem Anhang werden, sofern mir nichts entgangen ist, Axiome nicht in der Definition einer Struktur erwähnt, also nichts worauf sich der Begriff "Konsistenz" anwenden ließe. |
... Axiome wären irrelevant.
| Zitat: | | Our standard model of physics includes everyday mathematical structures such as the integers (defined by the Peano axioms) |
| Zitat: | | There are often many mathematical structures that are described by (“are models of”) a given formal system; for example, all specific groups are models of the formal system containing only the group axioms. Conversely, several formal systems may be equivalent descriptions of the same mathematical structure — e.g. gives examples of this. |
Ob ich alle Relationen explizit angebe, oder ob ich Axiome verwende, um sie zu generieren, ist doch letztlich unerheblich (außer dass mal das eine und mal das andere praktischer ist).
Tegmark spricht von “self-consistency”; worauf bezieht sich diese deiner Meinung nach, wenn nicht auf Axiome? und deren Verwendung im Rahmen einer / im Zuge der Definition oder Konstruktion einer mathematischen Struktur?
| index_razor hat Folgendes geschrieben: | | Meine Güte. Konsistenz eines Axiomensystems bedeutet, daß man nicht sowohl eine Aussage als auch ihre Negation formal aus den Axiomen beweisen kann. Diese Eigenschaft "überträgt" sich nicht auf Strukturen. |
Nein?
In welcher Beziehung steht denn die Konsistenz der natürlichen Zahlen zu der Konsistenz der Peano-Axiome?
| index_razor hat Folgendes geschrieben: | | Es ist nämlich Nonsens davon zu reden, z.B. eine arithmetische Aussage aus einer Menge von Zahlen zu beweisen. |
Warum?
Ich nehme i) eine Menge von Zahlen plus ii) Relationen / Axiome / Rechenregeln auf dieser Menge und beweise etwas.
Ohne (ii) ist es natürlich Nonsense, aber das habe ich auch nie behauptet.
| index_razor hat Folgendes geschrieben: | | Stattdessen folgt aus der Konsistenz von Axiomen, die Existenz einer Struktur, die alle Axiome erfüllt (mittels eines einfachen, aber nicht ganz trivialen Arguments). Ist das so schwer? |
Offensichtlich war es schwer, zu diesem Punkt zu gelangen.
Ich hatte dazu oben zitiert
| Zitat: | | Man kann die Peano-Axiome auch als Definition der natürlichen Zahlen auffassen. |
und sehe jetzt keine grundsätzliche Unstimmigkeit.
| index_razor hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | Ich verstehe‘s nicht.
Tegmark spricht von „self-consistent mathematical structures“
|
Wo denn? |
| index_razor hat Folgendes geschrieben: | | Kannst du definieren was die Phrase "inkonsistente Struktur" bedeutet oder mir sagen ob Tegmark sie irgendwo definiert? |
Hier:
https://arxiv.org/pdf/0704.0646.pdf
| Zitat: | Bearing these correspondences in mind, let us now discuss the Gödel-inspired worry mentioned above: that the MUH makes no sense because our universe would be somehow inconsistent or undefined. If one accepts David Hilbert’s dictum that “mathematical existence is merely freedom from contradiction” [126], then an inconsistent structure would not exist mathematically, let alone physically as in the MUH.
Our standard model of physics includes everyday mathematical structures such as the integers (defined by the Peano axioms) and real numbers. |
Ein Beispiel: Wie würdest du die "Dinge" bezeichnen, die Frege in "Grundgesetze der Arithmetik" diskutiert hat? Waren das zum Teil gar keine "mathematischen Strukturen"? Haben sie nie "existiert"? Immerhin wurde es aufgeschrieben. Ist es nicht naheliegend, diese teilweise als "inkonsistente mathematischen Strukturen" zu bezeichnen, wobei die Inkonsistenz durch Russell gezeigt wurde? Und dann festzustellen, dass diese "Dinge" nie im engeren d.h. Hilbertschen Sinne als "(konsistente) mathematische Strukturen" existiert haben?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 11. Jul 2022 11:31, insgesamt 11-mal bearbeitet |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18049
|
| TomS Verfasst am: 11. Jul 2022 09:56 Titel: |
|
|
| index_razor hat Folgendes geschrieben: | | Ich hatte nur ein Problem mit der Aussage "Eine Struktur existiert genau dann, wenn sie konsistent ist", da sie sinnlos ist. |
https://meiner-elibrary.de/media/upload/leseprobe/9783787304820.pdf
“Wenn sich die willkürlich gesetzten Axiome nicht einander widersprechen mit sämtlichen Folgen, so sind sie wahr, so existieren die durch die Axiome definierten Dinge. Das ist für mich das Criterium der Wahrheit und Existenz.”
Hilbert an Frege, 1899
https://archive.org/stream/bub_gb_z4c7AQAAIAAJ/bub_gb_z4c7AQAAIAAJ_djvu.txt
”In der Mathematik kann das Wort: ,existieren‘ nur einen Sinn haben: es bedeutet ,widerspruchsfrei sein‘“
Poincare, 1914 in “Wissenschaft und Methode”
| index_razor hat Folgendes geschrieben: | | Stattdessen folgt aus der Konsistenz von Axiomen, die Existenz einer Struktur, die alle Axiome erfüllt. |
Worüber genau sind wir uns jetzt uneinig?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 11. Jul 2022 18:26 Titel: |
|
|
| TomS hat Folgendes geschrieben: |
| index_razor hat Folgendes geschrieben: | | Stattdessen folgt aus der Konsistenz von Axiomen, die Existenz einer Struktur, die alle Axiome erfüllt. |
Worüber genau sind wir uns jetzt uneinig? |
Du scheinst zu denken (A) "Eine Struktur S existiert genau dann wenn S konsistent ist" sei eine sinnvolle Aussage. Vielleicht denkst du sogar sie besagt dasselbe wie (B) "Wenn P ein konsistentes Axiomensystem ist, existiert eine Struktur S, die P erfüllt". Beides ist falsch, d.h. (A) bedeutet nicht dasselbe wie (B) und nur (B) behauptet überhaupt irgendeinen Sachverhalt (der auch zutrifft). Die Aussage (A) ist vollkommen sinnlos. Ich kann auch kaum glauben, daß du den Unterschied nicht erkennst.
Betrachten wir mal ein Beispiel für die zweite Aussage (B): "Wenn die Peano-Axiome widerspruchsfrei sind, dann existiert eine Struktur, die sie erfüllt." Das ist sinnvoll und korrekt. Es existieren sogar viele Strukturen beliebiger Kardinalität größer gleich abzählbar, die die Peano-Axiome erfüllen. Die natürlichen Zahlen sind eine der abzählbaren Strukturen. Da es aber nicht-isomorphe Strukturen gibt (sowohl abzählbare als auch überabzählbare), kann man, denke ich, kaum sinnvoll davon sprechen, daß die Peano-Axiome die natürlichen Zahlen "definieren". Trotzdem folgt aus der Widerspruchsfreiheit der Peano-Axiome die Existenz der natürlichen Zahlen.
Ein Beispiel für die erste Aussage (A) wäre "Die natürlichen Zahlen existieren genau dann wenn die natürlichen Zahlen widerspruchsfrei sind." Ich habe jetzt mehrfach versucht zu erklären, warum das Unsinn ist. Die Peano-Arithmetik kann widerspruchsfrei sein, die natürlichen Zahlen nicht (sie können nur existieren oder nicht existieren). Vielleicht denkst du auch die natürlichen Zahlen seien irgendwie identisch mit der Peano-Arithmetik. Falls ja, wäre das ein fundamentaler Irrtum. Ungefähr so als würdest du die Keplerschen Gesetze mit dem Sonnensystem verwechseln. (Es ist sinnvoll von der Widerspruchsfreiheit der Keplerschen Gesetze zu reden. Aber zu behaupten, das Sonnensystem sei widerspruchsfrei, ist einfach konfus.)
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 11. Jul 2022 20:29 Titel: |
|
|
| TomS hat Folgendes geschrieben: |
Tegmark spricht von “self-consistency”; worauf bezieht sich diese deiner Meinung nach, wenn nicht auf Axiome? |
Ich meine und meinte immer "Selbstkonsistenz" bezieht sich auf Axiome. Du hattest hingegen gemeint, es bezöge sich auf Strukturen. Hier wieder:
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Meine Güte. Konsistenz eines Axiomensystems bedeutet, daß man nicht sowohl eine Aussage als auch ihre Negation formal aus den Axiomen beweisen kann. Diese Eigenschaft "überträgt" sich nicht auf Strukturen. |
Nein?
In welcher Beziehung steht denn die Konsistenz der natürlichen Zahlen zu der Konsistenz der Peano-Axiome?
|
Nochmal, "Konsistenz der natürlichen Zahlen" ist eine sinnlose Phrase. Ich habe keine Ahnung worauf du denkst, daß sie sich beziehen könnte.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Es ist nämlich Nonsens davon zu reden, z.B. eine arithmetische Aussage aus einer Menge von Zahlen zu beweisen. |
Warum?
Ich nehme i) eine Menge von Zahlen plus ii) Relationen / Axiome / Rechenregeln auf dieser Menge und beweise etwas.
|
Und jetzt nimm dieselbe Menge von Axiomen, ein paar Zahlen, ein paar Relationen und eine Glaskugel. Nun schmeiße die Zahlen, die Relationen und die Glaskugel wieder weg und behalte nur die Axiome. Dann kannst du noch exakt dasselbe beweisen wie vorher. Was sagt dir das? Aussagen kann man nur aus Aussagen beweisen, nicht mithilfe von Zahlen, Relationen oder Glaskugeln.
| Zitat: |
Ein Beispiel: Wie würdest du die "Dinge" bezeichnen, die Frege in "Grundgesetze der Arithmetik" diskutiert hat? Waren das zum Teil gar keine "mathematischen Strukturen"? Haben sie nie "existiert"? Immerhin wurde es aufgeschrieben. |
Ja, sie haben nie existiert. Ich nehme an, du meinst die potentiellen Referenten der aufgeschriebenen Zeichen. Die Zeichen selbst haben natürlich existiert (und tun es vermutlich noch).
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
|
Qubit
Anmeldungsdatum: 17.10.2019
Beiträge: 829
|
| Qubit Verfasst am: 11. Jul 2022 23:01 Titel: |
|
|
| index_razor hat Folgendes geschrieben: |
Ich habe keine Ahnung warum du mir dauernd die Definition von mathematischen Strukturen vorhältst. Ich weiß was das ist. Niemand außer dir, auch nicht Tegmark, definiert eine mathematische Struktur als "Menge plus Relationen plus Axiome" |
Ich habe jetzt hier nicht alles gelesen, vielleicht hast du es auch schon gesagt, aber was ist denn für dich dann eine "mathematische Struktur", wenn nicht eine Menge mit definierten Relationen (Verknüpfungen) und dafür vorgegebenen Axiomen?
Schon so eine typische Struktur wie der algebraische Körper ist doch so konstruiert..
| https://de.m.wikipedia.org/wiki/K%C3%B6rper_(Algebra) hat Folgendes geschrieben: |
Ein Körper ist eine Menge K, versehen mit zwei inneren zweistelligen Verknüpfungen „+“ und „*“ (die Addition und Multiplikation genannt werden), für die folgende Bedingungen erfüllt sind: [AXIOME]
|
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18049
|
| TomS Verfasst am: 12. Jul 2022 00:14 Titel: |
|
|
@index_razor -
Zunächst erkläre mir bitte den Unterschied:
| index_razor hat Folgendes geschrieben: | | (A) "Eine Struktur S existiert genau dann wenn S konsistent ist" … Die Aussage (A) ist vollkommen sinnlos. |
| Zitat: | | In der Mathematik kann das Wort: ,existieren‘ nur einen Sinn haben: es bedeutet ,widerspruchsfrei sein‘ |
| Zitat: | | If one accepts David Hilbert’s dictum that “mathematical existence is merely freedom from contradiction”, then an inconsistent structure would not exist mathematically … |
Warum ist die Aussage (A) sinnlos, im Gegensatz zu Poincares Aussage bezogen auf eine mathematische Struktur S? Was stört an Tegmarks Aussage?
| index_razor hat Folgendes geschrieben: | Man kann aber folgendes sagen: 1) Jede konsistente Menge von Axiomen besitzt ein Modell.
2) Eine inkonsistente Menge von Axiomen besitzt kein Modell.
Das ist der Zusammenhang zwischen der Konsistenz eines Axiomensystems und der Existenz einer Struktur. Du (und Tegmark) verballhornst das zur "Konsistenz einer Struktur" und bringst damit zwei vollkommen verschiedene Dinge durcheinander. |
Wenn es darauf rausläuft, dass Tegmark, Poincare und ich gleichermaßen unsauber formulieren, dann kann ich gut damit leben.
Da wir uns bei deinen und meinen Aussagen im Kreis drehen, könntest du außerdem mal die zitierten Aussagen kommentieren:
| Zitat: | | Ein Körper ist eine Menge K, versehen mit zwei inneren zweistelligen Verknüpfungen „+“ und „*“ (die Addition und Multiplikation genannt werden), für die folgende Bedingungen erfüllt sind: [AXIOME] … |
| Zitat: | | Eine algebraische Struktur ist ein geordnetes Paar bestehend aus einer nichtleeren Menge A und einer Familie innerer Verknüpfungen auf A. Die Eigenschaften der konkret gegebenen Verknüpfungen einer Algebra spezifiziert man näher durch Axiome … |
| Zitat: | | Die Menge der natürlichen Zahlen bildet mit der Addition und der Multiplikation zusammen eine mathematische Struktur, die als kommutativer Halbring bezeichnet wird … Die Peano-Arithmetik (erster Stufe) ist eine Theorie der Arithmetik, also der natürlichen Zahlen, innerhalb der Prädikatenlogik erster Stufe. Als Axiome werden die Peano-Axiome verwendet … |
| Zitat: | | A mathematical structure is a set (or sometimes several sets) with various associated mathematical objects such as subsets, sets of subsets, operations and relations, all of which must satisfy various requirements (axioms). |
Ich hatte bisher den Eindruck, das verstanden und korrekt wiedergegeben zu haben.
Erwähnenswert ist m.E., dass Axiome nicht zwingender Bestandteil der Definition sind, sondern dass die Relationen alleine ausreichen. Z.B. kann man eine Gruppe durch eine Verknüpfungstabelle definieren, ohne sich auf die Gruppenaxiome zu beziehen (sind diese nicht erfüllt, liegt keine Gruppe jedoch immer noch eine mathematische Struktur vor). Jedenfalls erfordert eine mathematische Struktur neben einer Menge einen weiteren Satz von Regeln für Relationen, Verknüpfung etc.
Ich sehe weiterhin kein Problem, allenfalls sprachliche Ungenauigkeiten.
Beispiel: Wenn die Anwendungen der Rechenregeln für + und * der natürlichen Zahlen nie widersprüchliche Ergebnisse liefert, dann bezeichne ich die natürlichen Zahlen als konsistent. Dabei verstehe ich “die natürlichen Zahlen“ wie oben z.B. als geordnetes Paar bestehend aus einer nichtleeren Menge N = {0,1,2,…} und einer Familie innerer Verknüpfungen {+,*} auf A.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 12. Jul 2022 08:24 Titel: |
|
|
| Qubit hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: |
Ich habe keine Ahnung warum du mir dauernd die Definition von mathematischen Strukturen vorhältst. Ich weiß was das ist. Niemand außer dir, auch nicht Tegmark, definiert eine mathematische Struktur als "Menge plus Relationen plus Axiome" |
Ich habe jetzt hier nicht alles gelesen, vielleicht hast du es auch schon gesagt, aber was ist denn für dich dann eine "mathematische Struktur", wenn nicht eine Menge mit definierten Relationen (Verknüpfungen) und dafür vorgegebenen Axiomen? |
Nur die Menge M und die Relationen. Streng genommen kommt noch eine Abbildung hinzu, die angibt, welches n-stellige Relationssymbol bzw. Funktionssymbol zu welcher n-stelligen Relation bzw. Funktion auf M gehört. (Falls es noch Konstanten gibt, wird jeder davon ein Element aus M zugeordnet.) Die präzise Definition ist hier.
Für eine gegebene Signatur S und eine Menge A von S-Axiomen kann man natürlich die Frage stellen welche S-Strukturen A erfüllen. Das definiert ein Prädikat auf der Menge von S-Strukturen, nämlich "erfüllt A" oder "ist ein 'A'". Dieses Prädikat kann man sich durch die Axiome A definiert vorstellen. Aber es umfaßt im allgemeinen sehr viele verschiedene S-Strukturen und definiert nicht eine einzelne davon. Beispiel: Ar=(s,0) bestehe aus einem einstelligen Funktionssymbol und einer Konstanten. Die Peano-Axiome sind eine Menge von Ar-Sätzen und definieren das Prädikat "ist eine Peano-Arithmetik" auf der Menge aller Ar-Strukturen. Aber sie definieren natürlich nicht eine bestimmte Struktur, wie z.B. die natürlichen Zahlen.
Wenn man sagt "Diese und jene Axiome definieren eine Struktur 'A'" dann meint man vermutlich genau, daß die Axiome A das Prädikat "ist ein 'A'" auf einer Menge von Strukturen definieren. Das ist tatsächlich nicht mehr als eine sprachliche Ungenauigkeit und nicht mein Kritikpunkt. Aber zu behaupten eine S-Struktur (oder eine Menge von Strukturen definiert über ein solches Prädikat) sei widerspruchsfrei, ist eine völlig andere Kategorie von Unsinn.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
|
Vice Versa
Anmeldungsdatum: 20.06.2022
Beiträge: 34
|
| Vice Versa Verfasst am: 12. Jul 2022 09:07 Titel: |
|
|
Index_razor und TomS
Ihr beide seit lustig. Meinungs/Wissens-Diskussionen in Textform sind immer sehr sehr heikel. Mann wird in den meisten Fällen mistverstanden und man "redet" aneinander vorbei... Nur schon bei der verbalen Kommunikation kann das ein Problem sein, aber dort ist die "Verständniseffizenz" bedeutend höher  |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 12. Jul 2022 10:28 Titel: |
|
|
| TomS hat Folgendes geschrieben: | @index_razor -
Zunächst erkläre mir bitte den Unterschied:
| index_razor hat Folgendes geschrieben: | | (A) "Eine Struktur S existiert genau dann wenn S konsistent ist" … Die Aussage (A) ist vollkommen sinnlos. |
| Zitat: | | In der Mathematik kann das Wort: ,existieren‘ nur einen Sinn haben: es bedeutet ,widerspruchsfrei sein‘ |
| Zitat: | | If one accepts David Hilbert’s dictum that “mathematical existence is merely freedom from contradiction”, then an inconsistent structure would not exist mathematically … |
Warum ist die Aussage (A) sinnlos, im Gegensatz zu Poincares Aussage bezogen auf eine mathematische Struktur S? Was stört an Tegmarks Aussage?
|
Ich bin mir nicht sicher was Poincare meint. Im Gegensatz zu dir erwähnt er keine "Strukturen". Es ist also möglich, daß er meint Widerspruchsfreiheit eines Dings sei gleichbdeutend mit der Exitenz eines anderen Dings. (Das wäre nicht sinnlos und dasselbe was ich auch behaupte.) Ich kann mir schwer vorstellen (aber auch nicht ausschließen), daß er meint Widerspruchsfreiheit eines Dings sei gleichbedeutend mit der Existenz desselben Dings. Denn handelt es sich bei diesem Ding z.B. um eine Menge von Axiomen, dann steht die Existenz außer frage. Und außerdem existieren widersprüchliche Axiomensysteme genauso gut wie widerspruchsfreie. Die Aussage wäre also offensichtlich falsch. Noch unwahrscheinlicher finde ich, daß er Satz (A) gemeint hat. Ich glaube innerhalb der Mathematik und Logik hat kaum jemand "Widerspruchsfreiheit" auf etwas anderes bezogen als auf eine Menge von Sätzen.
| Zitat: |
| index_razor hat Folgendes geschrieben: | Man kann aber folgendes sagen: 1) Jede konsistente Menge von Axiomen besitzt ein Modell.
2) Eine inkonsistente Menge von Axiomen besitzt kein Modell.
Das ist der Zusammenhang zwischen der Konsistenz eines Axiomensystems und der Existenz einer Struktur. Du (und Tegmark) verballhornst das zur "Konsistenz einer Struktur" und bringst damit zwei vollkommen verschiedene Dinge durcheinander. |
Wenn es darauf rausläuft, dass Tegmark, Poincare und ich gleichermaßen unsauber formulieren, dann kann ich gut damit leben.
|
Seit Poincares Aussage haben Gödel, Skolem und andere ein paar wichtige Beiträge zu den hier diskutierten Themen geleistet, auf die sich Tegmark zum Teil bezieht. Ich verstehe nicht, warum du dich nicht lieber mit dem Thema auseinandersetzt, anstatt über hundert Jahre alte Zitate rauszukramen, die aus einer Zeit stammen, bevor die revolutionärsten Arbeiten auf dem Gebiet überhaupt publiziert wurden. Tegmark hat das sicher getan und man kann über eine einzige unsaubere Formulierung hinwegsehen.
| Zitat: |
Da wir uns bei deinen und meinen Aussagen im Kreis drehen, könntest du außerdem mal die zitierten Aussagen kommentieren:
| Zitat: | | Ein Körper ist eine Menge K, versehen mit zwei inneren zweistelligen Verknüpfungen „+“ und „*“ (die Addition und Multiplikation genannt werden), für die folgende Bedingungen erfüllt sind: [AXIOME] … |
| Zitat: | | Eine algebraische Struktur ist ein geordnetes Paar bestehend aus einer nichtleeren Menge A und einer Familie innerer Verknüpfungen auf A. Die Eigenschaften der konkret gegebenen Verknüpfungen einer Algebra spezifiziert man näher durch Axiome … |
|
Siehe dazu meine Antwort an Qubit. Ich weiß allerdings nicht genau worauf du hinauswillst.
| Zitat: |
| Zitat: | | Die Menge der natürlichen Zahlen bildet mit der Addition und der Multiplikation zusammen eine mathematische Struktur, die als kommutativer Halbring bezeichnet wird … Die Peano-Arithmetik (erster Stufe) ist eine Theorie der Arithmetik, also der natürlichen Zahlen, innerhalb der Prädikatenlogik erster Stufe. Als Axiome werden die Peano-Axiome verwendet … |
|
Das ist genau was ich sage. Beachte den Unterschied zwischen 1) der Menge der natürlichen Zahlen inklusive Funktionen (eine mathematische Struktur) und 2) der Peano-Arithmetik (eine Theorie). Das ist genau der Unterschied auf den ich dich ganz zu Anfang hinweisen wollte und den du dich seither weigerst einzusehen. Widerspruchsfreiheit bezieht sich auf Theorien wie die Peano-Arithmetik, nicht auf Strukturen wie die natürlichen Zahlen.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18049
|
| TomS Verfasst am: 12. Jul 2022 11:30 Titel: |
|
|
Ja, wir drehen uns im Kreis.
Zunächst mal ich weiterhin der Meinung, dass es sich um eine sprachliche Unsauberkeit handelt.
Das fängt m.E. bei dir an, denn
| Zitat: | | (1) die Menge der natürlichen Zahlen (eine mathematisch Struktur) |
ist für sich betrachtet m.E. keine mathematische Struktur.
Es gilt - siehe oben - "a mathematical structure is a set with various associated mathematical objects such as ... operations and relations, all of which must satisfy various requirements (axioms)" bzw. "die Menge der natürlichen Zahlen bildet mit der Addition und der Multiplikation zusammen eine mathematische Struktur".
Insofern ist die Menge der natürlichen Zahlen alleine wohl auch weder konsistent noch inkonsistent.
Also reden wir doch besser von der Menge
und der Struktur
)
Nehmen wir nun an, die folgende Aussage
wäre beweisbar, was im Widerspruch zur ebenfalls beweisbaren Aussage
steht.
Dann wäre das, was ich zum Beweis herangezogen habe, widersprüchlich.
Herangezogen habe ich sicher nicht nur die Menge, sondern die Menge mit den darauf definierten Operationen und deren Eigenschaften (wie z.B. Kommutativität etc.)
Ich fasse das nun so auf, dass die Struktur
inkonsistent wäre.
Nun kannst du gerne folgendes tun: du führst Definitionen D und eine Menge von Axiomen A ein, mittels derer die Menge N sowie Verknüpfungen darauf konstruiert werden können. Wenn nun eine Inkonsistenz vorliegt, dann darfst du gerne behaupten, dass A für sich betrachtet inkonsistent ist.
Möglicherweise ist das genau das, was du meinst, und möglicherweise ist das der formal präzise Weg. Ich sehe den Unterschied übrigens sehr wohl ein, ich sehe nur nicht, dass er für die Diskussion wirklich relevant bzw. was an meiner Denkweise wirklich problematisch ist.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 12. Jul 2022 11:36 Titel: |
|
|
| TomS hat Folgendes geschrieben: | Ja, wir drehen uns im Kreis.
Zunächst mal ich weiterhin der Meinung, dass es sich um eine sprachliche Unsauberkeit handelt.
Das fängt m.E. bei dir an, denn
| Zitat: | | (1) die Menge der natürlichen Zahlen (eine mathematisch Struktur) |
ist für sich betrachtet m.E. keine mathematische Struktur.
|
Da ich befürchtet hatte, daß du dich daran aufhängst, hatte ich inzwischen ergänzt "inklusive Funktionen", so wie ich es vorher schon mehrmals getan hatte. Ich dachte irgendwann ist der Punkt mal rübergekommen und ich muß mich nicht jedesmal so umständlich ausdrücken.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 12. Jul 2022 12:17 Titel: |
|
|
| TomS hat Folgendes geschrieben: |
Insofern ist die Menge der natürlichen Zahlen alleine wohl auch weder konsistent noch inkonsistent.
Also reden wir doch besser von der Menge
und der Struktur
|
Bis hierhin keine relevanten Einwände. Ich habe in meiner Antwort an Qubit nochmal genauer definiert was ich unter einer Struktur verstehe und einen Link gepostet, der es noch präziser definiert. (Es wäre schön gewesen, wenn du das in deiner Kritik berücksichtigt hättest, wenn ich schon darauf hinweise.)
| Zitat: |
Nehmen wir nun an, die folgende Aussage
wäre beweisbar, was im Widerspruch zur ebenfalls beweisbaren Aussage
steht.
|
Ich nehme im folgenden an, "beweisbar" heißt mit den Peano-Axiomen beweisbar.
| Zitat: |
Dann wäre das, was ich zum Beweis herangezogen habe, widersprüchlich.
Herangezogen habe ich sicher nicht nur die Menge, sondern die Menge mit den darauf definierten Operationen und deren Eigenschaften (wie z.B. Kommutativität etc.)
|
Nein, herangezogen hättest du ausschließlich Sätze (die Peano-Axiome). Und diese Sätze wären es, die widersprüchlich sind, sonst nichts.
| Zitat: |
Ich fasse das nun so auf, dass die Struktur
inkonsistent wäre.
|
Wenn die Peano-Axiome widersprüchlich sind, dann existiert überhaupt keine Struktur, die sie erfüllt. "Die Struktur " bezieht sich dann also auf gar nichts. So, als würdest du von "dem runden Quadrat" reden. Es ist weder rund noch quadratisch. Es existiert schlicht nicht, hat also auch keine Eigenschaften.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt
Zuletzt bearbeitet von index_razor am 12. Jul 2022 13:02, insgesamt 2-mal bearbeitet |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18049
|
| TomS Verfasst am: 12. Jul 2022 12:46 Titel: |
|
|
| index_razor hat Folgendes geschrieben: | | Da ich befürchtet hatte, daß du dich daran aufhängst, hatte ich inzwischen ergänzt "inklusive Funktionen", so wie ich es vorher schon mehrmals getan hatte. |
Ok, damit ist das Missverständnis ausgeräumt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Qubit
Anmeldungsdatum: 17.10.2019
Beiträge: 829
|
| Qubit Verfasst am: 12. Jul 2022 13:26 Titel: |
|
|
| index_razor hat Folgendes geschrieben: | Die präzise Definition ist hier.
|
Beziehst du dich also dann auf die sog. "Modelltheorie"?
| Wikipedia hat Folgendes geschrieben: |
In universal algebra and in model theory, a structure consists of a set along with a collection of finitary operations and relations that are defined on it.
Universal algebra studies structures that generalize the algebraic structures such as groups, rings, fields and vector spaces. The term universal algebra is used for structures with no relation symbols.
Model theory has a different scope that encompasses more arbitrary theories, including foundational structures such as models of set theory. From the model-theoretic point of view, structures are the objects used to define the semantics of first-order logic. For a given theory in model theory, a structure is called a model if it satisfies the defining axioms of that theory, although it is sometimes disambiguated as a semantic model when one discusses the notion in the more general setting of mathematical models. Logicians sometimes refer to structures as interpretations.
|
In Modelltheorie bin ich nicht so firm. Aber so wie ich es verstehe, geht man auf recht abstraktem Level von einem Kalkül (formalen System) aus mit zugrundeliegenden Alphabeten/Symbolen, zwischen denen auf "syntaktischer" Ebene formale Relationen vorgegeben sind (Axiome).
Die Frage der Modelltheorie ist nun für mich, ob und welche Modelle (Semantiken) solchen formalen Systemen entsprechen, eben mathematische Strukturen wie zB. Mengen mit Relationen oder geometrische Modelle (zB. mit/ohne Parallelenaxiom).
Im Sinne der Modelltheorie sollte so tatsächlich wohl ein Modell ausreichen, um die Widerspruchsfreiheit des formalen Systems (inkl. Axiome) zu erbringen.
Kannst du nun daraus auf mathematische Strukturen der Natur schliessen? |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18049
|
| TomS Verfasst am: 12. Jul 2022 13:28 Titel: |
|
|
| index_razor hat Folgendes geschrieben: | | Bis hierhin keine relevanten Einwände. |
Danke.
| index_razor hat Folgendes geschrieben: | | Ich nehme im folgenden an, "beweisbar", heißt mit den Peano-Axiomen beweisbar. |
Möglich, aber nicht unbedingt unmittelbar mittels der Peano-Axiome.
Evtl. verwende ich einfach nur die Rechenregeln: https://de.wikipedia.org/wiki/Halbring_(algebraische_Struktur)
| index_razor hat Folgendes geschrieben: | | Zitat: | Dann wäre das, was ich zum Beweis herangezogen habe, widersprüchlich.
Herangezogen habe ich sicher nicht nur die Menge, sondern die Menge mit den darauf definierten Operationen und deren Eigenschaften (wie z.B. Kommutativität etc.) |
Nein, herangezogen hättest du ausschließlich Sätze (die Peano-Axiome). Und diese Sätze wären es, die widersprüchlich sind, sonst nichts |
Wieso? Vielleicht rechne ich ja einfach:
 = \ldots = 0)
| index_razor hat Folgendes geschrieben: | | Zitat: |
Ich fasse das nun so auf, dass die Struktur
inkonsistent wäre. |
Wenn die Peano-Axiome widersprüchlich sind, dann existiert überhaupt keine Struktur, die sie erfüllt. "Die Struktur " bezieht sich dann also auf gar nichts. So, als würdest du von "dem runden Quadrat" reden. Es ist weder rund noch quadratisch. Es existiert schlicht nicht, hat also auch keine Eigenschaften. |
Das ist mir schon klar, das ist ja letztlich die Aussage von Hilbert u.a.
Trotzdem habe ich ein Gebilde
das ich als mathematische Struktur bezeichne und mit dem ich arbeite, bis ich ich nach einiger Zeit mit Schrecken feststelle, dass ich damit zu Inkonsistenzen gelange. Und dann veröffentliche ich einen Artikel "The mathematical structure of the natural numbers is inconsistent". Du würdest mir im Peer Review anraten, den Titel in "The mathematical structure of the natural numbers does not exist" abzuändern.
Im Original sagt Hilbert übrigens "Ich bin nun überzeugt, daß es gelingen muß, einen direkten Beweis für die Widerspruchslosigkeit der arithmetischen Axiome zu finden …"
Also nochmal, mir ist der Unterschied durchaus klar.
Wie gesagt, ich halte "konsistente Struktur" für einen verkürzten und ggf. formal angreifbaren Sprachgebrauch, der jedoch an der Sache selbst wenig ändert.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 12. Jul 2022 16:44 Titel: |
|
|
| TomS hat Folgendes geschrieben: |
| index_razor hat Folgendes geschrieben: | | Ich nehme im folgenden an, "beweisbar", heißt mit den Peano-Axiomen beweisbar. |
Möglich, aber nicht unbedingt explizit.
|
Es wäre auf jeden Fall hilfreich, wenn wir uns auf ein Axiomensystem festlegen. Das müssen nicht unbedingt die Peano-Axiome sein, aber irgendeins benötigen wir um etwas zu beweisen (siehe unten). Und da du selbst in deinem letzten Beitrag keins erwähnt hast, habe ich sie vorgeschlagen. Wir können natürlich auch die Axiome von Halbringen verwenden.
| Zitat: |
Evtl. verwende ich einfach nur die Rechenregeln: https://de.wikipedia.org/wiki/Halbring_(algebraische_Struktur)
| index_razor hat Folgendes geschrieben: | | Zitat: | Dann wäre das, was ich zum Beweis herangezogen habe, widersprüchlich.
Herangezogen habe ich sicher nicht nur die Menge, sondern die Menge mit den darauf definierten Operationen und deren Eigenschaften (wie z.B. Kommutativität etc.) |
Nein, herangezogen hättest du ausschließlich Sätze (die Peano-Axiome). Und diese Sätze wären es, die widersprüchlich sind, sonst nichts |
Wieso? Vielleicht rechne ich ja einfach:
|
Die "Rechenregeln" der Halbringe sind Axiome. Was du als "einfaches Rechnen" bezeichnest, ist auf formaler Ebene nichts anderes als die Anwendung von Schlußregeln auf diese Axiome. Nehmen wir z.B. das erste Distributivgesetz. Das zugehörige Axiom lautet
=a\cdot b + a\cdot c )
Deine Gleichungskette ist, wieder auf formaler Eben, eine Folge von Sätzen. (Die Symbole "0", "1", "2" erfordern strenggenommen sogenannte Definitionserweiterungen der Sprache der Halbringe. Aber davon sehe ich jetzt mal ab, weil es vermutlich keine große Rolle spielt.) In dem Artikel sieht das alles ein bißchen anders aus, weil er nicht streng innerhalb eines formalen Systems arbeitet. Er benutzt z.B. auch naive Mengenlehre um Sachverhalte, die nichts mit den Axiomen der Halbgruppe zu tun haben, wie  etc. auf nicht formale Weise auszudrücken. Das ist auch vollkommen in Ordnung, denn es geht ja dort nicht um die Untersuchung von Strukturen und Axiomensystemen allgemein, wie in dieser Diskussion, sondern nur um Halbringe.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Zitat: |
Ich fasse das nun so auf, dass die Struktur
inkonsistent wäre. |
Wenn die Peano-Axiome widersprüchlich sind, dann existiert überhaupt keine Struktur, die sie erfüllt. "Die Struktur " bezieht sich dann also auf gar nichts. So, als würdest du von "dem runden Quadrat" reden. Es ist weder rund noch quadratisch. Es existiert schlicht nicht, hat also auch keine Eigenschaften. |
Das ist mir schon klar, das ist ja letztlich die Aussage von Hilbert u.a.
Trotzdem habe ich ein Gebilde
das ich als mathematische Struktur bezeichne und mit dem ich arbeite, bis ich ich nach einiger Zeit mit Schrecken feststelle, dass ich damit zu Inkonsistenzen gelange.
|
Nein, genauso ist es nicht. Das Gebilde, mit dem du arbeitest sind Axiome und Schlußregeln. Du nimmst höchstens an, daß es eine Struktur gibt, die alle diese Axiome erfüllt. (Die Annahme kann gute Gründe haben, wie im Falle der natürlichen Zahlen.) Diese Hoffnung zerschlägt sich in dem Moment, in dem du einen Widerspruch in deinen Axiomen feststellst. Aber der Widerspruch war natürlich schon immer da, und irgendeine zugehörige Struktur hat nie existiert. Alle deine Symbole "0", "1", etc. sind sinnlos und waren es schon immer. Sie designieren rein gar nichts.
In deiner Vorstellung verwechselst du wirklich genau die Theorie mit der Struktur. (Eine Theorie ist es strenggenommen nur, wenn sie erfüllbar, also widerspruchsfrei ist.) Die Theorie ist nichts weiter als Sätze zusammengsetzt aus Zeichen nach festgelegter Syntax. (Sie existiert deshalb natürlich immer, man muß es nicht beweisen.) Die Struktur ist das, worauf sich eine konsistente Menge von Sätzen beziehen kann.
| Zitat: |
Und dann veröffentliche ich einen Artikel "The mathematical structure of the integers is inconsistent". Du würdest mir im Peer Review anraten, den Titel in "The mathematical structure of the integers does not exist" abzuändern. |
Es ist mehr als nur eine Sprechweise. Du bist der Meinung, du hättest "konsistente/inkonsistente Struktur" sinnvoll definiert. Das hast du bisher nicht, und ich denke auch nicht, daß das möglich ist. Du ordnest einfach willkürlich irgendeiner Struktur ein Axiomensystem zu -- wahrscheinlich ist dir nicht klar, daß dies vollkommen willkürlich ist --, und erklärst dann die Konsistenz/Inkonsistenz dieses Axiomensystems zur "Konsistenz/Inkonsistenz" der Struktur. Dies sagt aber absolut gar nichts über die betrachtete Struktur aus, sondern ausschließlich über das gewählte Axiomensystem.
Betrachten wir das Vorgehen mal genauer und bleiben wir zur Konkretisierung bei der Signatur ) . (Wichtig: " " und " " sind jetzt Symbole, keine Funktionen.) Nun gibt es eine Menge S-Strukturen, d.h. eine Menge von Mengen mit je zwei zweistelligen Funktionen drauf. Ich glaube wir sind und inzwischen einig, daß an diesen Strukturen "an sich" nichts konsistent oder inkonsistent ist.
Andererseits gibt es unabhängig davon eine Menge von S-Sätzen, wie z.B.  oder auch  . Beliebige solcher Sätze kann man zu Axiomensystemen zusammenfassen. Einige davon sind konsistent und einige unter den konsistenten definieren wiederum das Prädikat "ist ein Halbring". Andere sind inkonsistent und definieren gar nichts, bzw. das leere Prädikat, welches auf nichts zutrifft.
Nun meine Frage: gegeben irgendeine S-Struktur ) (hier stehen nun die Funktionen), wie entscheidest du, ob es sich um eine "konsistente" oder eine "inkonsistente" Struktur handelt? Dafür brauchst du ein S-Axiomensystem. Aber welches? Ich habe nicht vorausgesetzt, daß ein Halbring ist. Ich habe gar nichts vorausgesetzt, außer daß es eine S-Struktur ist, also zwei Funktionen existieren, um deutlich zu machen, daß die Struktur selbst vollkommen unabhängig von irgendwelchen Axiomen ist.
| Zitat: |
Im Original sagt Hilbert übrigens "Ich bin nun überzeugt, daß es gelingen muß, einen direkten Beweis für die Widerspruchslosigkeit der arithmetischen Axiome zu finden …"
|
Das ist eine sinnvolle Aussage.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt
Zuletzt bearbeitet von index_razor am 12. Jul 2022 18:57, insgesamt einmal bearbeitet |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 12. Jul 2022 17:14 Titel: |
|
|
| Qubit hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | Die präzise Definition ist hier.
|
Beziehst du dich also dann auf die sog. "Modelltheorie"?
|
Ja, ganz genau.
| Zitat: |
Kannst du nun daraus auf mathematische Strukturen der Natur schliessen? |
Als Schlußfolgerung würde ich es nicht bezeichnen (mein "Beweis" weiter oben war ja nicht ganz todernst gemeint), aber ich denke Indizien gibt es dafür schon. Die Naturwissenschaften machen ja mathematische Aussagen über die Natur. Ich denke diese Aussagen lassen sich im Prinzip formalisieren. Wenn wir nun eine Theorie besitzen und Grund zu der Annahme haben, daß alle Aussagen dieser Theorie auf die Natur zutreffen, dann muß die Natur eine mathematische Struktur sein. Die "Theorie" hier muß nicht mal eine besonders allgemeine Theorie sein, wie die ART oder das Standardmodell (bzw. Formalisierungen davon). Es kann im Prinzip eine Aufzählung von Fakten sein. Es muß auf keinen Fall eine Theorie sein, aus der sich alle Fakten über die Natur ableiten lassen (also keine TOE). Sowas besitzen wir nämlich für die natürlichen Zahlen auch nicht und werden es auch nie.*)
Ich kann aber nicht genau sagen, welche Eigenschaften so eine Theorie haben müßte, damit der Schluß gerechtfertigt wäre, die Natur als mathematische Struktur anzusehen. (Vielleicht hat Tegmark dazu auch ein paar Ideen.)
Ich kann mir aber andererseits auch nicht vorstellen, welche Eigenschaften die Natur haben könnte, die es absolut ausschließen würden, daß es sich um eine mathematische Struktur handelt. Egal welche Tatsachen wir über die Natur herausfinden, ich behaupte, man kann diese Tatsachen so weit in formalen Sätzen ausdrücken, daß diese Sätze Teil einer mathematischen Theorie sind. Die Natur ist dann also ein "Modell" (im Sinne der Modelltheorie) für diese Theorie und damit eine mathematische Struktur.
_____________
EDIT: *) Hier muß man etws vorichtig formulieren. Natürlich gibt es Theorien, aus denen sich sämtliche Fakten über die natürlichen Zahlen ableiten lassen. Was ich meine sind effektiv axiomatisierbare Theorien.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
|
Haudegen007
Gast
|
| Haudegen007 Verfasst am: 13. Jul 2022 07:32 Titel: |
|
|
Hallo zusammen, nachdem ich aus dieser Diskussion aussteigen musste, habe ich abschließend noch eine Frage: Ist jetzt die folgende Antwort, die mir TomS am Sonntag gegeben hat, korrekt oder hat sich durch die Diskussion nochmal etwas geändert?
| TomS hat Folgendes geschrieben: | | Haudegen007 hat Folgendes geschrieben: | | Das die Phänomene, die wir in der Physik beschreiben/vorhersagen können, in irgendeiner Form mathematisch strukturiert sind, kann ich nun akzeptieren. |
Das tut jeder Physiker.
Der Realist sagt jedoch zudem, dass eine unabhängig von dem ihm zugänglichen Phänomenen objektive Realität existiert. Und ein Physiker, der diese Einstellung hat, wird zudem behaupten, dass die Mathematik eben nicht ausschließlich ein Werkzeug zur Berechnung von Phänomenen ist, sondern dass die gewisse Aspekte dieser objektiven Realität zutreffend beschreibt.
Bsp. QCD: die SU(3) Eichsymmetrie ist in den Phänomenen der Kern- und Teilchenphysik praktisch völlig unsichtbar, dennoch würde der Realist behaupten, diese SU(3) Eichsymmetrie sei ein Aspekt der Realität (es gibt nicht den einen Realismus sondern verschiedene Spielarten).
| Haudegen007 hat Folgendes geschrieben: | | Tegmarks These, alles sei Mathematik, teile ich aber nicht. |
Der Realist würde so etwas sagen wie gewisse Aspekte der objektiv gegebenen Realität werden durch mathematische Strukturen treu / isomorph / zutreffend beschrieben.
Tegmark sagt im wesentlichen, die Realität ist wesensidentisch mit einer mathematischen Struktur.
Am Beispiel oben: die SU(3) sei nicht nur - wie für den Realisten - eine Struktur, die zu bestimmten Aspekten der objektiv gegebenen Realität isomorph ist, sondern - nach Tegmark - die Realität ist identisch mit dieser SU(3) Eichtheorie (natürlich kann das für die SU(3) Eichtheorie nicht stimmen, da sie offensichtlich nicht alle Aspekte der Realität umfasst).
Tegmark hat natürlich das Problem, warum eine ganz bestimmte mathematische Struktur tatsächlich existiert, und was es überhaupt bedeutet, dass diese Struktur existiert. Diese Existenz kann ja nichts sein, was man als zusätzliche Eigenschaft einführt, es muss in der Struktur selbst bereits enthalten sein. Tegmark löst das Problem dadurch, dass er die physikalische und die mathematische Existenz ebenfalls identifiziert, d.h. eine mathematische Struktur existiert dann und nur dann, wenn sie konsistent ist, und genau dann ist sie auch physikalisch existent (was nichts anderes ist als mathematisch existent, die Unterscheidung wird sinnlos). Damit gelangt er zum Mathematischen Multiversum: die physikalische Realität ist wesensidentisch mit der Gesamtheit aller konsistenten mathematischen Strukturen.
(Ich hoffe, meine Erinnerung an das Buch ist einigermaßen zutreffend)
Das unterschreiben sicher nur wenige Physiker und Philosophen. |
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18049
|
| TomS Verfasst am: 13. Jul 2022 08:37 Titel: |
|
|
Vorab:
Ich habe nochmals darüber nachgedacht, woher die Idee stammt, von der Konsistenz einer mathematischen Struktur zu sprechen. Ich denke, es hat damit zu tun, die Definition bzw. Konstruktion der fundamentalen mathematischen Objekte von der Definition weiterer auf diesen Objekten wirkenden Regeln zu trennen. Als Physiker ist man damit vertraut, in Objekten zu denken, die physikalische Sachverhalte beschreiben, z.B. Vektoren oder Funktionen. Diese – zusammen mit elementaren Rechenregeln, die der Mathematiker als Axiome einführen würde – dienen als Ausgangspunkt. Weitere Regeln zur Modellierung physikalischer Sachverhalte ändern die zugrundeliegenden Objekte und die für sie geltenden Regeln nicht.
Während der Mathematiker also einen Satz von Axiomen betrachtet und zu damit verträglichen bzw. durch diese definierten Strukturen gelangt, geht der Physiker gewisser maßen zweistufig vor: er setzt auf diesen Strukturen auf und erweitert sie. Dabei steht oft nicht die mathematische Konsistenz sondern die physikalische Anwendbarkeit im Vordergrund.
(Natürlich ist klar, dass diese physikalische Vorgehensweise bei Tegmarks Ansatz nicht mehr durchgehalten werden kann).
Bsp. Quantenmechanik
Der Physiker denkt in Wellenfunktionen und deren Zeitentwicklung, dafür gelten die bekannten Regeln für den Hilbertraum der quadratintegrablen Funktionen mit einer Familie unitärer Operatoren U(t), d.h. es liegt eine mathematische Struktur
 \right))
vor.
Zur Repräsentation von Observablen (Messgrößen) werden selbstadjungierte Operatoren A eingeführt, die auf den Wellenfunktionen wirken, d.h.
Und genau das geht teilweise schief, da Operatoren die unangenehme Eigenschaft haben können, dass
Erst in diesem Fall ändert der Physiker die zugrundeliegende Struktur, in dem er einen "größeren" Raum zulässt und/oder bestimmte problematische Wellenfunktionen als unphysikalisch ignoriert.
Das ist nun weder eine Inkonsistenz im Sinne Tegmarks, noch eine mathematisch präzise Vorgehensweise; und m.W.n. kann die Vorgehensweise in der nicht-relativistischen Quantenmechanik geeignete formalisiert werden, so dass sie den mathematischen Ansprüchen genügt. Es zeigt jedoch, woher die Idee stammt: man verwendet eine bestehende "konsistente Struktur" und führt darauf zusätzliche Regeln ein. Treten dabei keine Inkonsistenzen auf, so "ist die so erweiterte Struktur konsistent".
Man könnte das für eine Menge M und Regeln R symbolisch wie folgt schreiben:
 \to S^\ast = (S, R^\ast))
Es wird die Verträglichkeit der neuen Regeln R* mit der existierenden Struktur S betrachtet.
Der Mathematiker denkt eher in
 \to (R, R^\ast))
d.h. betrachtet die Konsistenz der Regeln (Axiome) R und R*.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18049
|
| TomS Verfasst am: 13. Jul 2022 08:58 Titel: |
|
|
| Haudegen007 hat Folgendes geschrieben: | | Hallo zusammen, nachdem ich aus dieser Diskussion aussteigen musste, habe ich abschließend noch eine Frage: Ist jetzt die folgende Antwort, die mir TomS am Sonntag gegeben hat, korrekt oder hat sich durch die Diskussion nochmal etwas geändert? |
Die philosophische Frage haben wir hier kaum erörtert.
1) Ich bin weiterhin der Meinung, dass Tegmark tatsächlich (zunächst) mathematische und physikalische Existenz identifiziert, d.h. alles das, was mathematisch existiert, existiert auch als physikalisch Realität. Beide Realitäten sind identisch: "Our external physical reality is a mathematical structure" - nicht: "Our external physical reality is represented as a mathematical structure". Sein Kriterium für mathematische und zugleich physikalische Existenz ist (zunächst) Widerspruchsfreiheit.
2) Tegmark betrachtet im Folgenden jedoch einen modifizierten physikalischen Existenzbegriff, wobei er nicht Widerspruchsfreiheit sondern Berechenbarkeit als Existenzkriterium zugrundelegt. Das haben wir noch nicht erörtert.
3) Nach der Diskussion mit index_razor muss man das Folgende
| TomS hat Folgendes geschrieben: | | ... dass er die physikalische und die mathematische Existenz ebenfalls identifiziert, d.h. eine mathematische Struktur existiert dann und nur dann, wenn sie konsistent ist ... |
mathematisch präzisieren.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 13. Jul 2022 12:00 Titel: |
|
|
| TomS hat Folgendes geschrieben: | Vorab:
Ich habe nochmals darüber nachgedacht, woher die Idee stammt, von der Konsistenz einer mathematischen Struktur zu sprechen. Ich denke, es hat damit zu tun, die Definition bzw. Konstruktion der fundamentalen mathematischen Objekte von der Definition weiterer auf diesen Objekten wirkenden Regeln zu trennen.
|
Was genau meinst du denn mit "Regeln"? Mir ist nicht klar geworden ob du damit Aussagen über eine Struktur meinst oder Operationen auf der Struktur (oder noch etwas anderes). Du scheinst zwischen diesen beiden Auffassungen zu schwanken und die fehlende Unterscheidung könnte das Hauptproblem sein.
Man könnte z.B. das Distributivgesetz als Rechenregel bezeichnen. Es handelt sich um eine Aussage über zwei Operationen auf einer Struktur. Wie schon gesagt, können verschiedene solcher Aussage widersprüchlich sein. Widersprüchliche Aussagen können aber natürlich nicht auf ein und dieselbe Struktur zutreffen. Also entweder gilt das Distributivgesetz in Struktur X oder es gilt eine Aussage, die dem Distributivgesetz widerspricht in Struktur X. Die zutreffende der beiden Aussagen beschreibt quasi eine Eigenschaft der Operationen auf der Struktur. Aber die Operationen selbst können unmöglich widersprüchliche Eigenschaften haben.
Wenn du also mit einer konkreten Struktur anfängst, kann es niemals zu irgendwelchen Widersprüchen kommen. (Alle Aussagen, die dich interessieren sind wahre Aussagen über deine Struktur. Und eine Menge von wahren Aussagen kann nie widersprüchlich sein.) Die Frage der Widersprüchlichkeit einer Aussagenmenge stellt sich überhaupt nur, wenn die Existenz bestimmter Modelle fraglich ist. Das ist für die gewöhnliche Mathematik eine vermutlich eher exotische Situation. Denn schließlich denkt man sich nicht einfach so irgendwelche Axiome aus. Stattdessen startet man mit einer Struktur und trägt Aussagen zusammen, die von der Struktur erfüllt werden. Das ist auch genau der Zusammenhang zwischen den natürlichen Zahlen und den Peano-Axiomen. Die Peano-Axiome sind eine nachträgliche und, wie inzwischen bekannt ist, notwendigerweise unvollständige Beschreibung der natürlichen Zahlen. Die Unvollständigkeit ermöglicht die Existenz von Nichtstandardmodellen der Arithmetik. Aber diese Modelle sind wiederum ein eher esoterisches Thema. Für die meisten Teile der Mathematik ist nur wichtig, welche Aussagen auf die natürlichen Zahlen zutreffen (also wahr sind), nicht welche Aussagen man z.B. aus den Peano-Axiomen beweisen kann (und die folglich in allen Modellen gelten). (Sollte sich z.B. herausstellen das Fermats Theorem nicht aus den Peano-Axiomen folgt, wird das trotzdem keinerlei Zweifel an der Gültigkeit der Aussage verursachen.)
| Zitat: | | Es zeigt jedoch, woher die Idee [der inkonsistenten Strukturen] stammt: man verwendet eine bestehende "konsistente Struktur" und führt darauf zusätzliche Regeln ein. Treten dabei keine Inkonsistenzen auf, so "ist die so erweiterte Struktur konsistent". |
Das ergibt immer noch keinen Sinn für mich. Ich kann mir vorstellen, was eine erweiterte Struktur ist: vielleicht eine Struktur mit größerem Träger oder mehr Operationen/Relationen. Aber ich habe absolut keine Ahnung wie eine erweiterte Struktur "inkonsistenter" sein könnte als die ursprüngliche Struktur. Eine "konsistente Struktur" ist einfach eine Struktur. Nehmen wird doch mal ein konkretes Beispiel einer ziemlich langweiligen Struktur bestehend aus einem Element und einer zweistelligen Operation \mapsto e)) . Jetzt kann ich mir ein paar Aussagen überlegen, die auf X zutreffen, z.B.
(1) 
wobei " " das Symbol für die zweistellige Funktion auf X ist. Oder
(2) 
was besagt, daß der Träger von X nur ein Element enthält. Jetzt erweitere ich die Struktur um ein Element, so daß
\mapsto a, (a,a)\mapsto e, (e,a)\mapsto a, (e,e)\mapsto e)) .
Nun gelten andere Aussagen, z.B. die Negation von (2). Aber (1) gilt immer noch. Zu jeder konkreten Struktur (X oder X') gibt es höchstens einen Widerspruch zwischen Aussagen, die auf diese Struktur zutreffen und Aussagen, die nicht zutreffen. Letztere sind aber irrelevant für diese Struktur.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
|
Haudegen007
Gast
|
| Haudegen007 Verfasst am: 13. Jul 2022 19:23 Titel: |
|
|
| TomS hat Folgendes geschrieben: |
1) Ich bin weiterhin der Meinung, dass Tegmark tatsächlich (zunächst) mathematische und physikalische Existenz identifiziert, d.h. alles das, was mathematisch existiert, existiert auch als physikalisch Realität. Beide Realitäten sind identisch: "Our external physical reality is a mathematical structure" - nicht: "Our external physical reality is represented as a mathematical structure". Sein Kriterium für mathematische und zugleich physikalische Existenz ist (zunächst) Widerspruchsfreiheit.
|
Alles klar, so hatte ich ihn nämlich auch verstanden. Ich denke mir, nur weil z.B. Materie mathematischen Strukturen unterliegt, müssen Materie und mathematische Struktur noch nicht identisch sein. |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 13. Jul 2022 19:54 Titel: |
|
|
| Haudegen007 hat Folgendes geschrieben: |
Ich denke mir, nur weil z.B. Materie mathematischen Strukturen unterliegt, müssen Materie und mathematische Struktur noch nicht identisch sein. |
Die mathematische Struktur wäre in diesem Fall ein Modell für eine (hinreichend formalisierte) physikalische Theorie, wie z.B. das Standardmodell oder eben eine TOE, nicht "Materie". Wenn es tatsächlich so eine TOE gibt, dann wäre die Realität ebenfalls ein Modell und damit eine mathematische Struktur.
P.S. Das "ist" in "Die Realität ist eine mathematische Struktur" bedeutet bei Tegmark übrigens "bis auf Isomorphie gleich" (siehe Abschnitt II D)
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt
Zuletzt bearbeitet von index_razor am 14. Jul 2022 07:11, insgesamt 2-mal bearbeitet |
|
|
Haudegen007
Gast
|
| Haudegen007 Verfasst am: 13. Jul 2022 20:08 Titel: |
|
|
@ index_razor
Für dich ist also die Ansicht Tegmarks unausweichlich richtig, wenn die Physik hinreichend korrekte Naturbeschreibungen liefert, oder wie ist das zu verstehen? Für dich gibt es so gesehen auch keine Materie, sondern alles ist wesensidentisch mit der Mathematik?[/quote] |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 13. Jul 2022 20:18 Titel: |
|
|
| Haudegen007 hat Folgendes geschrieben: | @ index_razor
Für dich ist also die Ansicht Tegmarks unausweichlich richtig, wenn die Physik hinreichend korrekte Naturbeschreibungen liefert, oder wie ist das zu verstehen?
|
Nicht unausweichlich. Die Voraussetzung war "es gibt eine hinreichend formalisierbare TOE". Das ist nicht gerade unausweichlich. Ich denke aber auch ohne diese Voraussetzung sind die Indizien ziemlich stark (siehe meine zweite Antwort an Qubit weiter oben.)
| Zitat: |
Für dich gibt es so gesehen auch keine Materie, sondern alles ist wesensidentisch mit der Mathematik? |
Zu diesem "wesensidentisch" siehe das P.S. aus meinem vorigen Beitrag (bzw. Abschnitt D im MUH-paper "The Mathematical Universe").
Die MUH (zumindest meine Auffassung davon) schließt nicht aus, daß es Materie gibt. Es schließt die Existenz von gar nichts aus. Wenn die Realität z.B. eine Substruktur für eine Quantenfeldtheorie enthält, dann könnte man Materie als "Konfiguration von Fermionenfeldern" o.ä. definieren.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18049
|
| TomS Verfasst am: 13. Jul 2022 20:30 Titel: |
|
|
| index_razor hat Folgendes geschrieben: | | Was genau meinst du denn mit "Regeln"? Mir ist nicht klar geworden ob du damit Aussagen über eine Struktur meinst oder Operationen auf der Struktur. Du scheinst zwischen diesen beiden Auffassungen zu schwanken und die fehlende Unterscheidung könnte das Hauptproblem sein. |
Nee, im Gegenteil.
Gerade wenn man Aussagen zur Definition bzw. Konstruktion der Struktur von Operationen auf der Struktur trennen kann, vereinfacht sich das Bild ganz erheblich. M.E. ist das in der Physik ohnehin zumeist der Fall.
| index_razor hat Folgendes geschrieben: | | Man könnte z.B. das Distributivgesetz als Rechenregel bezeichnen. Es handelt sich um eine Aussage über zwei Operationen auf einer Struktur. Wie schon gesagt, können verschiedene solcher Aussage widersprüchlich sein. Widersprüchliche Aussagen können aber natürlich nicht auf ein und dieselbe Struktur zutreffen. Also entweder gilt das Distributivgesetz in Struktur X oder es gilt eine Aussage, die dem Distributivgesetz widerspricht in Struktur X. Die zutreffende der beiden Aussagen beschreibt quasi eine Eigenschaft der Operationen auf der Struktur. Aber die Operationen selbst können unmöglich widersprüchliche Eigenschaften haben. |
Klar.
| index_razor hat Folgendes geschrieben: | | Zitat: | | Es zeigt jedoch, woher die Idee [der inkonsistenten Strukturen] stammt: man verwendet eine bestehende "konsistente Struktur" und führt darauf zusätzliche Regeln ein. Treten dabei keine Inkonsistenzen auf, so "ist die so erweiterte Struktur konsistent". |
Das ergibt immer noch keinen Sinn für mich. Ich kann mir vorstellen, was eine erweiterte Struktur ist: vielleicht eine Struktur mit größerem Träger oder mehr Operationen/Relationen. Aber ich habe absolut keine Ahnung wie eine erweiterte Struktur "inkonsistenter" sein könnte als die ursprüngliche Struktur. |
Nicht „inkonsistenter“; entweder konsistent oder inkonsistent.
Und es handelt sich doch nur um unpräzisen Sprachgebrauch;und der Begriff „consistent structure“ wird einfach immer wieder verwendet, nicht nur von mir.
Beispiel: ich betrachte (M, +) und gehe zu (M, +, *) mit Distributivgesetz über; das kann funktionieren oder auch nicht. Man kann nun (+, *) mit Distributivgesetz betrachten und ungeeignete Mengen M verwerfen, oder man kann (M, +, *) für ungeeignete Mengen M als „inkonsistent“ bezeichnen und dann verwerfen.
Ich sehe nach wie vor keinen für mich relevanten Unterschied, ich gestehe aber zu, dass ich damit formal einen Fehler begehe oder zumindest schlampig formuliere.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 13. Jul 2022 20:46 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Was genau meinst du denn mit "Regeln"? Mir ist nicht klar geworden ob du damit Aussagen über eine Struktur meinst oder Operationen auf der Struktur. Du scheinst zwischen diesen beiden Auffassungen zu schwanken und die fehlende Unterscheidung könnte das Hauptproblem sein. |
Nee, im Gegenteil.
Gerade wenn man Aussagen zur Definition bzw. Konstruktion der Struktur von Operationen auf der Struktur trennen kann, vereinfacht sich das Bild ganz erheblich.
|
Ja, eben. Dein letzter Beitrag hat das für mich nicht klar getrennt. Was meintest du denn nun mit "Regel"? (Übrigens, "Aussagen, die eine Struktur definieren bzw. konstruieren" läßt mich wieder nichts gutes ahnen. Wie kommst du auf sowas?)
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Zitat: | | Es zeigt jedoch, woher die Idee [der inkonsistenten Strukturen] stammt: man verwendet eine bestehende "konsistente Struktur" und führt darauf zusätzliche Regeln ein. Treten dabei keine Inkonsistenzen auf, so "ist die so erweiterte Struktur konsistent". |
Das ergibt immer noch keinen Sinn für mich. Ich kann mir vorstellen, was eine erweiterte Struktur ist: vielleicht eine Struktur mit größerem Träger oder mehr Operationen/Relationen. Aber ich habe absolut keine Ahnung wie eine erweiterte Struktur "inkonsistenter" sein könnte als die ursprüngliche Struktur. |
Nicht „inkonsistenter“; entweder konsistent oder inkonsistent.
|
Ich meinte auch lediglich, daß "inkonsistent" inkonsistenter ist als "konsistent". Sorry, für die schlechte Ausdrucksweise.
Also nochmal, du startest mit irgendeiner Struktur und erweiterst sie irgendwie. In dem von dir beschriebenen Szenario kann es niemals zu irgendeiner Inkonsistenz kommen. Und eine "konsistente Struktur" ist einfach eine Struktur.
| Zitat: |
Und es handelt sich doch nur um unpräzisen Sprachgebrauch;und der Begriff „consistent structure“ wird einfach immer wieder verwendet, nicht nur von mir.
|
Das mag ja sein. Aber wenn es sinnvoller Sprachgebrauch wäre, dann ließe er sich präzisieren. Das scheint aber nicht der Fall zu sein. Die einzige sinnvolle Interpretation, die mir einfällt, macht das "konsistent" in "konsistente Struktur" zu einem bedeutungslosen Füllwort und "inkonsistente Struktur" zu einem runden Quadrat.
| Zitat: |
Beispiel: ich betrachte (M, +) und gehe zu (M, +, *) mit Distributivgesetz über; das kann funktionieren oder auch nicht.
|
Und hier hast du mich schon verloren. Wie genau sieht dieser Übergang aus und wie kann es möglich sein, daß er nicht funktioniert? Können wir vielleicht bei dem einfachen Beispiel bleiben, daß ich in meinem letzten Beitrag eingeführt habe? Wenn es in irgendeiner Art inadäquat ist, dann erkläre mir bitte genau inwiefern.
| Zitat: |
Man kann nun (+, *) mit Distributivgesetz betrachten und ungeeignete Mengen M verwerfen, oder man kann (M, +, *) für ungeeignete Mengen M als „inkonsistent“ bezeichnen und dann verwerfen.
|
Du redest anscheinend davon irgendwas zu "verwerfen", das gar nicht existiert. Etwas Nichtexistentes kannst du natürlich bezeichnen wie du willst, von mir aus auch als "inkonsistent". Das einzige Problem ist, daß jede Aussage über etwas Nichtexistentes falsch ist.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt
Zuletzt bearbeitet von index_razor am 15. Jul 2022 09:10, insgesamt 3-mal bearbeitet |
|
|
|
|
Registrieren
Login
FAQ
Suchen
