| Autor |
Nachricht |
Mathology
Anmeldungsdatum: 18.10.2013
Beiträge: 415
|
 Mathology Verfasst am: 13. Apr 2017 18:19 Titel: Zwei Federn und ein Massestück Mathology Verfasst am: 13. Apr 2017 18:19 Titel: Zwei Federn und ein Massestück |
 |
|
...
Zuletzt bearbeitet von Mathology am 06. Jul 2017 15:28, insgesamt einmal bearbeitet |
|
 |
willyengland
Anmeldungsdatum: 01.05.2016
Beiträge: 715
|
 willyengland Verfasst am: 13. Apr 2017 21:06 Titel: willyengland Verfasst am: 13. Apr 2017 21:06 Titel: |
 |
|
Ich würde sagen F1 ist 1,7 N und F2 ist 1,5 N.
Wozu man die Gewichtskraft der ersten Feder braucht, ist mir nicht klar.
 cm)
Ohne Gewähr ...
_________________
Gruß Willy |
|
 |
Derfnam
Gast
|
 Derfnam Verfasst am: 13. Apr 2017 21:21 Titel: Derfnam Verfasst am: 13. Apr 2017 21:21 Titel: |
 |
|
| willyengland hat Folgendes geschrieben: |
Wozu man die Gewichtskraft der ersten Feder braucht, ist mir nicht klar. |
Es ist die unbelastete Länge angegeben. unter der eigenen Gewichtskraft wird sich die Zugfeder etwas längen (so deute ich die Angabe)
|
|
 |
willyengland
Anmeldungsdatum: 01.05.2016
Beiträge: 715
|
 willyengland Verfasst am: 13. Apr 2017 23:10 Titel: willyengland Verfasst am: 13. Apr 2017 23:10 Titel: |
 |
|
Ok, nur wie errechnet man dieses "etwas längen"?
_________________
Gruß Willy |
|
 |
Derfnam
Gast
|
 Derfnam Verfasst am: 14. Apr 2017 08:28 Titel: Derfnam Verfasst am: 14. Apr 2017 08:28 Titel: |
 |
|
| willyengland hat Folgendes geschrieben: | | Ok, nur wie errechnet man dieses "etwas längen"? |
f= G/C
f= 0,2N/0,15 N/cm = 1,33 cm.
Die senkrecht hängende Zugfeder längt sich durch das Eigengewicht um 1,33 cm.
|
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 14. Apr 2017 11:14 Titel: Huggy Verfasst am: 14. Apr 2017 11:14 Titel: |
 |
|
| Derfnam hat Folgendes geschrieben: | | willyengland hat Folgendes geschrieben: | | Ok, nur wie errechnet man dieses "etwas längen"? |
f= G/C
f= 0,2N/0,15 N/cm = 1,33 cm.
Die senkrecht hängende Zugfeder längt sich durch das Eigengewicht um 1,33 cm. |
Das ist nicht richtig, denn das Gewicht der Feder greift nicht an ihrem unteren Ende an, sondern verteilt über die Federlänge. Man muss daher die lokalen Längenänderungen der Feder durch das Gewicht des darunterliegenden Teils aufintegrieren. Mit einer von unten nach oben verlaufenden x-Koordinate und
L = Länge der Feder
G = Gewicht der Feder
D = Federkonstante
erhält man für die lokale Längenänderung an der Position x
= \frac {G}{DL^2}xdx)
Die gesamte Längenänderung unter ihrem Eigengewicht ist

also nur halb so groß, als wenn das gesamte Gewicht am unteren Ende angreifen würde.
|
|
 |
Derfnam
Gast
|
 Derfnam Verfasst am: 14. Apr 2017 13:39 Titel: Derfnam Verfasst am: 14. Apr 2017 13:39 Titel: |
 |
|
| Huggy hat Folgendes geschrieben: | | Derfnam hat Folgendes geschrieben: | | willyengland hat Folgendes geschrieben: | | Ok, nur wie errechnet man dieses "etwas längen"? |
f= G/C
f= 0,2N/0,15 N/cm = 1,33 cm.
Die senkrecht hängende Zugfeder längt sich durch das Eigengewicht um 1,33 cm. |
Das ist nicht richtig, denn das Gewicht der Feder greift nicht an ihrem unteren Ende an, sondern verteilt über die Federlänge. Man muss daher die lokalen Längenänderungen der Feder durch das Gewicht des darunterliegenden Teils aufintegrieren. Mit einer von unten nach oben verlaufenden x-Koordinate und
L = Länge der Feder
G = Gewicht der Feder
D = Federkonstante
erhält man für die lokale Längenänderung an der Position x
= \frac {G}{DL^2}xdx)
Die gesamte Längenänderung unter ihrem Eigengewicht ist

also nur halb so groß, als wenn das gesamte Gewicht am unteren Ende angreifen würde. |
Könnte sein.
Die Gewichtskraft greift im SP der Feder an. Und der liegt in der Mitte der Federlänge.
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 14. Apr 2017 17:39 Titel: Myon Verfasst am: 14. Apr 2017 17:39 Titel: |
 |
|
| Derfnam hat Folgendes geschrieben: | Könnte sein.
Die Gewichtskraft greift im SP der Feder an. Und der liegt in der Mitte der Federlänge. |
Wieso das denn? Eine Feder ist kein starrer Körper und es geht auch nicht um eine Translation der Feder; die Gravitationskraft greift letztendlich an jedem Elementarteilchen an. Huggys Integral ist daher sicher richtig. Ob die Aufgabe tatsächlich so gelöst werden soll, geht aus der Aufgabenstellung nicht klar hervor. Konsequenterweise müsste dann auch bei der unteren Feder so verfahren werden.
|
|
 |
Derfnam
Gast
|
 Derfnam Verfasst am: 14. Apr 2017 17:48 Titel: Derfnam Verfasst am: 14. Apr 2017 17:48 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | | Derfnam hat Folgendes geschrieben: | Könnte sein.
Die Gewichtskraft greift im SP der Feder an. Und der liegt in der Mitte der Federlänge. |
Wieso das denn? Eine Feder ist kein starrer Körper und es geht auch nicht um eine Translation der Feder; die Gravitationskraft greift letztendlich an jedem Elementarteilchen an. |
Das hat doch niemand bestritten.
Ein langes, senkrecht hängendes Seil längt sich doch auch bereits unter dem Einfluß des Eigengewichtes.
[as_string: @Derfnam: kannst Du bitte drauf achten, dass Du beim Zitieren auch das schließende quote-Endtag in Deinen Beiträgen korrekt mit rein schreibst. Das funktionioert irgendwie bei Deinen Beiträgen ganz häufig nicht und ich hab es schon ein paar Male selbst ergänzt, weil man sonst nicht so genau sieht, bis wo ein Zitat geht und ab wo Dein Text anfängt. Verwende besser erst die Vorschau und überprüfe Deine Beiträge, bevor Du sie dann endgültig abschickst.]
|
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 15. Apr 2017 07:55 Titel: Huggy Verfasst am: 15. Apr 2017 07:55 Titel: |
 |
|
@Derfnam
Es würde deinem physikalischen Verständnis helfen, wenn du dir klar machst, dass man erst nach Integration der lokalen Dehnungen wissen kann, das eine Rechnung, bei der man das Gewicht der Feder in ihrem Schwerpunkt angreifen lässt, zu dem richtigen Ergebnis führt. Vorher ist das eine reine Vermutung. Es stimmt auch nur, weil eine lineare Federkennlinie angesetzt wird. Bei einer nicht linearen Kennlinie stimmt es nicht.
|
|
 |
Derfnam
Gast
|
 Derfnam Verfasst am: 15. Apr 2017 10:27 Titel: Re: Zwei Federn und eine Massestück Derfnam Verfasst am: 15. Apr 2017 10:27 Titel: Re: Zwei Federn und eine Massestück |
 |
|
| Mathology hat Folgendes geschrieben: | Gegeben sind zwei Schraubenfedern. Die erste ist im unbelasteten Zustand 20 cm lang. Sie hat eine Federhärte von 0,15 N/ cm und eine Gewichtskraft von 0,25 N. Die zweite Feder ist im unbelasteten Zustand 35 cm lang, hat eine
Federhärte von 0,08 N / cm und eine Gewichtskraft von 0,20 N. Die erste Feder hängt an einem Haken. An ihrem unteren Ende wird die zweite Feder befestigt.
Wie lang sind beide Federn zusammen, wenn nun noch an das Ende der zweiten
Feder ein Massenstück gehängt wird, dessen Gewichtskraft 1,5 N beträgt ?
Meine Rechnung ist diese:
Auf die erste Feder wirkt die Kraft der zweiten Feder und des Gewichtsstücks. Also 0,2+1,5 = 1,7 N
Das teile ich durch die Federkonstante 0,15N der ersten Feder und erhalte

Auf die zweite Feder wirkt nur die Kraft des Massestücks also 1,5N. Dann aheb ich 1,5 / 0,08 = 18,75 cm gerechnet.
Alles zusammen addiert mit der länge im unbelasteten zustand = 55cm+11,3cm+18,75cm= 85,05 cm.
Ist das richtig? |
Hallo Mathology,
mach dir mal Gedanken über die Schaltungsart der Federn in deiner Aufgabe.
Vorschlag.
Gruß:
Manni
| Beschreibung: |
|

Download |
| Dateiname: |
20170415Image_00690.pdf |
| Dateigröße: |
98.12 KB |
| Heruntergeladen: |
421 mal |
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 15. Apr 2017 11:41 Titel: Re: Zwei Federn und eine Massestück as_string Verfasst am: 15. Apr 2017 11:41 Titel: Re: Zwei Federn und eine Massestück |
 |
|
| Derfnam hat Folgendes geschrieben: | Hallo Mathology,
mach dir mal Gedanken über die Schaltungsart der Federn in deiner Aufgabe.
Vorschlag. |
Wobei das bei der hier gestellten Aufgabe, bei der die Federn ein Eigengewicht haben und deshalb die Kraft jeweils unterschiedlich auf die Federn wirkt, ja gerade nicht hilfreich ist. Deine Reihenschaltung geht ja vom Ansatz her gerade davon aus, dass auf beide Federn dieselbe Kraft wirkt.
Gruß
Marco
|
|
 |
Mathology
Anmeldungsdatum: 18.10.2013
Beiträge: 415
|
 Mathology Verfasst am: 15. Apr 2017 13:59 Titel: Mathology Verfasst am: 15. Apr 2017 13:59 Titel: |
 |
|
Also was denn jetzt? haha 
|
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 15. Apr 2017 14:38 Titel: Huggy Verfasst am: 15. Apr 2017 14:38 Titel: |
 |
|
Mal selber ein ganz klein wenig denken ist wohl nicht?
Es gibt zwei Varianten:
a) Man berücksichtigt die Dehnung der Federn unter ihrem Eigengewicht.
b) Man tut dies nicht.
a) Ist meiner Meinung nach wahrscheinlicher im Sinne des Aufgabenstellers. Aber für beide Varianten enthalten die bisherigen Beiträge alles, was man für die Lösung braucht.
|
|
 |
Derfnam
Gast
|
 Derfnam Verfasst am: 15. Apr 2017 14:46 Titel: Re: Zwei Federn und eine Massestück Derfnam Verfasst am: 15. Apr 2017 14:46 Titel: Re: Zwei Federn und eine Massestück |
 |
|
| as_string hat Folgendes geschrieben: | | Derfnam hat Folgendes geschrieben: | Hallo Mathology,
mach dir mal Gedanken über die Schaltungsart der Federn in deiner Aufgabe.
Vorschlag. |
Wobei das bei der hier gestellten Aufgabe, bei der die Federn ein Eigengewicht haben und deshalb die Kraft jeweils unterschiedlich auf die Federn wirkt, ja gerade nicht hilfreich ist. Deine Reihenschaltung geht ja vom Ansatz her gerade davon aus, dass auf beide Federn dieselbe Kraft wirkt.
Gruß
Marco |
Menschenskind, was hast du den immer zu klötern ohne selbst konkret etwas zu posten?
Das Eigengewicht der Federn kann er doch zusätzlich berücksichtigen und ergänzend in die Rechnung einfließen lassen. Grundsätzlich ist es doch erst einmal sinnvoll, ihm die Kenntnis unterschiedlicher Feder- Schaltungen zu vermitteln.
Rechne ihm das selbst vor, wenn du an meinen postings was zu meckern hast.
Hier wird viel heiße Luft produziert und verwirrt, anstatt praktisch zuhandeln.
Typisch "Schule" also;-)
Du siehst ja, was Mathology jetzt geantwortet hat.
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 15. Apr 2017 16:33 Titel: Re: Zwei Federn und eine Massestück as_string Verfasst am: 15. Apr 2017 16:33 Titel: Re: Zwei Federn und eine Massestück |
 |
|
| Derfnam hat Folgendes geschrieben: | | Menschenskind, was hast du den immer zu klötern ohne selbst konkret etwas zu posten? |
Es steht in diesem Thread eigentlich schon alles drin. Nur Deine in diesem Kontext falschen Ansätze bringen letztlich die Verwirrung.
Soll er denn mit Deiner Formel rechnen und dann die Eigenmassen der Feder einfach weg lassen oder wie?
Wenn Du ständig etwas falsches schreibst, muss halt irgendjemand das sagen, tut mir ja auch leid, dass das bei Deinen Posts so oft nötig ist!
| Derfnam hat Folgendes geschrieben: | | Das Eigengewicht der Federn kann er doch zusätzlich berücksichtigen und ergänzend in die Rechnung einfließen lassen. |
Aber dann kann er doch mit der Rechnung der Parallel- und Reihenschaltung nichts anfangen, weil er diese Gewichtskräfte schon von Anfang an berücksichtigen müsste.
| Derfnam hat Folgendes geschrieben: | | Grundsätzlich ist es doch erst einmal sinnvoll, ihm die Kenntnis unterschiedlicher Feder- Schaltungen zu vermitteln. |
Ja, das stimmt. Aber wenn es nur grundsätzlich ist und mit der konkreten Aufgabe nur entfernt etwas zu tun hat, sollte man das zumindest deutlich dazu sagen, um eben gerade nicht zu verwirren!
| Derfnam hat Folgendes geschrieben: | Rechne ihm das selbst vor, wenn du an meinen postings was zu meckern hast.
Hier wird viel heiße Luft produziert und verwirrt, anstatt praktisch zuhandeln.
Typisch "Schule" also;-) |
Nein, Du hast eben den Sinn des Forums nicht verstanden: Es geht eben gerade nicht darum, es vor zu rechnen, sondern so viel Hinweise und Erklärungen zu geben, dass er es selbst hin bekommt. i. A. korrigiere ich nur, wenn jemand etwas falsches schreibt, damit es nicht in die falsche Richtung läuft. In letzter Zeit komme ich nicht so häufig dazu, einen Thread durchgängig zu bekleiden, so dass ich mich nicht stärker einbringen will. Aber bitte:
@Mathology:
Im Prinzip steht ja schon alles in diesem Thread, was Du brauchst.
- überlege Dir zuerst, welche Kräfte die untere Feder dehnt. Das ist die Gewichtskraft der angehängten Masse plus nach Huggys Rechnung die Hälfte der Gewichtskraft der Feder selbst. Das kannst Du in das Hooke'sche Gesetz einsetzen und hast die Verlängerung der unteren Feder.
- Für die obere Feder addierst Du wieder die Gewichtskräfte von dem was unten dran hängt, also die von der Masse plus der unteren Feder. Dann wieder die Hälfte der oberen Feder dazu und ins Hooke'sche Gesetz damit.
- Beide Verlängerungen zusammen addiert gibt die gesamte Verlängerung.
- Zur Gesamtverlängerung musst Du noch die Länge der Feder im entspannten Zustand addieren.
Gruß
Marco
|
|
 |
Derfnam
Gast
|
 Derfnam Verfasst am: 15. Apr 2017 22:06 Titel: Re: Zwei Federn und eine Massestück Derfnam Verfasst am: 15. Apr 2017 22:06 Titel: Re: Zwei Federn und eine Massestück |
 |
|
| as_string hat Folgendes geschrieben: | DerfnamSoll er denn mit Deiner Formel rechnen und dann die Eigenmassen der Feder einfach weg lassen oder wie?
Wenn Du ständig etwas falsches schreibst, muss halt irgendjemand das sagen, tut mir ja auch leid, dass das bei Deinen Posts so oft nötig ist!
[quote="Derfnam hat Folgendes geschrieben: | | Das Eigengewicht der Federn kann er doch zusätzlich berücksichtigen und ergänzend in die Rechnung einfließen lassen. |
Aber dann kann er doch mit der Rechnung der Parallel- und Reihenschaltung nichts anfangen, weil er diese Gewichtskräfte schon von Anfang an berücksichtigen müsste.
Gruß
Marco |
Hallo Marco,
er muß nicht von Anfang an damit rechnen, sondern kann das auch erst nachträglich einfließen lassen und ich schreibe auch nicht ständig etwas falsch.
Im übrigen bin ich mit 77 zu alt, um mich noch in "Hahnenkämpfe" verwickeln zu lassen.
Und ein Sendungsbewußtsein für einen Bildungsauftrag verspüre ich auch nicht
Ich werde daher nur noch gelegentlich mitlesen aber keine Vorschläge mehr posten.
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 16. Apr 2017 12:38 Titel: Re: Zwei Federn und eine Massestück as_string Verfasst am: 16. Apr 2017 12:38 Titel: Re: Zwei Federn und eine Massestück |
 |
|
| Derfnam hat Folgendes geschrieben: |
er muß nicht von Anfang an damit rechnen, sondern kann das auch erst nachträglich einfließen lassen |
Äh, verstehe ich nicht: Du präsentierst ihm einen Ansatz, der gleiche Kraft auf beide Federn voraussetzt meinst aber, das wäre nicht verwirrend, während ich darauf hinweise und Du Dich dann aufregst, weil ich verwirren würde? Wie bitte willst Du mit diesem falschen Ansatz anfangen und dann später noch die Massen berücksichtigen? Das was er gleich am Anfang gepostet hatte (was Du übrigens komplett zitiert hast) war da ja schon deutlich richtiger, als Dein Ansatz. Außer dass er die Längung der Federn aufgrund ihres jeweiligen Eigengewichts nicht berücksichtigt hat, wobei wir nicht sicher wissen, ob der Aufgabensteller das überhaupt berücksichtigt hat, stimmt ja seine Rechnung gleich am Anfang sogar.
| Derfnam hat Folgendes geschrieben: | | und ich schreibe auch nicht ständig etwas falsch. |
Naja, zumindest hier im Thread schon. Erst willst Du für die Längung einer Feder ihr komplettes Eigengewicht nehmen, was falsch ist, dann schreibst Du was von "Schwerkraft greift am Schwerpunkt an", was nur bei einem starren Körper einen Sinn ergibt, die Feder aber flexibel ist und dann kommst Du mit dem Ansatz ohne Eigengewicht der Feder, was hier ja schon gar nichts zur Sache tut. Meinst Du nicht, dass das alles eher zur Verwirrung beiträgt als sonst was?
| Derfnam hat Folgendes geschrieben: | Im übrigen bin ich mit 77 zu alt, um mich noch in "Hahnenkämpfe" verwickeln zu lassen.
Und ein Sendungsbewußtsein für einen Bildungsauftrag verspüre ich auch nicht
Ich werde daher nur noch gelegentlich mitlesen aber keine Vorschläge mehr posten. |
Tut mir leid, wenn ich Dich beleidigt oder verletzt habe oder so. Aber was soll ich machen, wenn ich sehe, dass jemand eine falsche oder zumindest missverständliche Antwort gibt? Ich kann das dann doch nicht einfach so lassen, oder? Eigentlich könntest Du mir auch für die Korrektur bzw. Ergänzung danken, das wäre die normale Reaktion. Mit Hahnenkampf hat das nun wirklich nichts zu tun. Tut mir leid, wenn Du das so empfindest!
Gruß
Marco
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 16. Apr 2017 17:04 Titel: GvC Verfasst am: 16. Apr 2017 17:04 Titel: |
 |
|
@as-string
Vielleicht hat Derfnam ja seine Rechtfertigung, dass man das Eigengewicht der Federn zusätzlich berücksichtigen und ergänzend in die Rechnung einfließen lassen könne, anders gemeint, als Du sie verstanden hast. Man kann ja durchaus zunächst die Verlängerung der Reihenschaltung der Federn mit Hilfe der Gesamtfederkonstante bestimmen, muss dann aber noch die jeweilige Verlängerung beider Federn infolge ihres Eigengewichtes und die Verlängerung der oberen Feder infolge des Gewichtes der unteren Feder dazu addieren. Derfnam hat ja nicht gesagt, dass man nur die jeweilge Eigenverlängerung addieren müsse.
Aber ob der TE überhaupt versteht, worüber hier diskutiert wird, ist eher fraglich.
|
|
 |
Derfnam
Gast
|
 Derfnam Verfasst am: 16. Apr 2017 17:22 Titel: Derfnam Verfasst am: 16. Apr 2017 17:22 Titel: |
 |
|
| GvC hat Folgendes geschrieben: | @as-string
Vielleicht hat Derfnam ja seine Rechtfertigung, dass man das Eigengewicht der Federn zusätzlich berücksichtigen und ergänzend in die Rechnung einfließen lassen könne, anders gemeint, als Du sie verstanden hast. Man kann ja durchaus zunächst die Verlängerung der Reihenschaltung der Federn mit Hilfe der Gesamtfederkonstante bestimmen, muss dann aber noch die jeweilige Verlängerung beider Federn infolge ihres Eigengewichtes und die Verlängerung der oberen Feder infolge des Gewichtes der unteren Feder dazu addieren. Derfnam hat ja nicht gesagt, dass man nur die jeweilge Eigenverlängerung addieren müsse.
|
@GvC
Gut so!
Genau so habe ich das gemeint, denn die Reihenfolge der Additionen von Einzeleinfederungen ist ja völlig egal. Man muss das nicht von Anfang an berücksichtigen.
Gruß:
Manni
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 16. Apr 2017 21:45 Titel: as_string Verfasst am: 16. Apr 2017 21:45 Titel: |
 |
|
| GvC hat Folgendes geschrieben: | @as-string
Vielleicht hat Derfnam ja seine Rechtfertigung, dass man das Eigengewicht der Federn zusätzlich berücksichtigen und ergänzend in die Rechnung einfließen lassen könne, anders gemeint, als Du sie verstanden hast. Man kann ja durchaus zunächst die Verlängerung der Reihenschaltung der Federn mit Hilfe der Gesamtfederkonstante bestimmen, muss dann aber noch die jeweilige Verlängerung beider Federn infolge ihres Eigengewichtes und die Verlängerung der oberen Feder infolge des Gewichtes der unteren Feder dazu addieren. |
Aber dass das möglich ist, muss man eigentlich auch erst einmal aufgrund der Linearität des Hookeschen Gesetz zeigen. So ganz selbstverständlich ist es ja nun nicht unbedingt.
| GvC hat Folgendes geschrieben: | | Derfnam hat ja nicht gesagt, dass man nur die jeweilge Eigenverlängerung addieren müsse. |
Das schlimme ist, und das war der Grund warum ich überhaupt gepostet hatte, dass Derfnams Post mit Parallelschaltung/Reihenschaltung als der Ansatz für diese Aufgabe von Mathology verstanden werden könnte und ich einfach nur klar machen sollte, dass es das dann eben noch nicht ist. Warum sich Derfnam dann gleich aufgeregt hat und mir vorgeworfen hat, ich hätte "immer zu klötern" (was auch immer das genau bedeuten mag) und ich würde ja selbst nichts konkretes posten, fand ich dann ziemlich unverschämt und konnte ich auch gar nicht verstehen.
Gruß
Marco
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 16. Apr 2017 23:51 Titel: GvC Verfasst am: 16. Apr 2017 23:51 Titel: |
 |
|
| as_string hat Folgendes geschrieben: | | Aber dass das möglich ist, muss man eigentlich auch erst einmal aufgrund der Linearität des Hookeschen Gesetz zeigen. So ganz selbstverständlich ist es ja nun nicht unbedingt. |
Na ja, dass es sich bei dem hier betrachteten Federsysten um ein lineares handelt, ist durch die beiden konstanten Federkonstanten vorgegeben. Und dass in linearen Systemen das Superpositionsprinzip gilt, ist eine physikalische Grundregel, die direkt aus der Summenregel der Differentialrechnung folgt. Insofern meine ich, dass die Gültigkeit des Superpositionsprinzips in linearen Systemen durchaus selbstverständlich ist.
| as_string hat Folgendes geschrieben: | | Warum sich Derfnam dann gleich aufgeregt hat und mir vorgeworfen hat, ich hätte "immer zu klötern" (was auch immer das genau bedeuten mag) und ich würde ja selbst nichts konkretes posten, fand ich dann ziemlich unverschämt und konnte ich auch gar nicht verstehen. |
Ja, der Ton gerät bei solchen Diskussionen zuweilen aus dem Gleis. Mit mir hat Derfnam das auch schon gemacht. Und mir selber ist das ebenfalls schon passiert. Das scheint einfach menschlich zu sein, weil wir nicht immer in der Lage sind, reine physikalische Logik von den uns Menschen (Gott sei Dank) eigenen Emotionen zu trennen.
Ich schlage deshalb vor, das Kriegsbeil zu begraben und erstmal grundsätzlich jedem, der hier auf Fragen antwortet, den Willen zur Hilfe zu unterstellen. Wenn diese Hilfe zuweilen in die falsche Richtung weist, kann man ja versuchen, das - möglichst emotionslos - zu korrigieren.
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 17. Apr 2017 09:59 Titel: as_string Verfasst am: 17. Apr 2017 09:59 Titel: |
 |
|
@GvC:
Du glaubst also, wenn ich Derfnams Post mit dem "Schaltungsartenanhang" hätte unkommentiert stehen lassen, dann hätte Mathology direkt gesehen: Ah super, das kann ich ja so nehmen und wegen der Linearität des Hookeschen Gesetzes addiere ich dann bei der einen Feder die Eigenlängung und bei der anderen die andere Eigenlängung plus die durch die andere Federgewichtskraft einfach dazu. Ist jetzt alles logisch klar...
Mal abgesehen davon, dass es für diese Aufgabe ein ziemlich umständlicher Weg wäre, würde Mathology da sicher nicht von selbst drauf kommen können.
Ich hätte es ok gefunden, wenn er noch dazu geschrieben hätte, dass bei diesem Ansatz die Eigengewichte der Federn noch nicht berücksichtigt ist und man diese getrennt berechnen und addieren kann. Aber sonst ist es einfach im besten Fall verwirrend und im schlechtesten irreführend.
Aber jetzt habe ich mich schon mehrfach wiederholt und das hilft keinem was. Ich werde mich jetzt einfach raus halten.
Gruß
Marco
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 17. Apr 2017 10:18 Titel: GvC Verfasst am: 17. Apr 2017 10:18 Titel: |
 |
|
| as_string hat Folgendes geschrieben: | @GvC:
Du glaubst also, wenn ich Derfnams Post mit dem "Schaltungsartenanhang" hätte unkommentiert stehen lassen, dann hätte Mathology direkt gesehen: Ah super, das kann ich ja so nehmen und wegen der Linearität des Hookeschen Gesetzes addiere ich dann bei der einen Feder die Eigenlängung und bei der anderen die andere Eigenlängung plus die durch die andere Federgewichtskraft einfach dazu. Ist jetzt alles logisch klar... |
Nein, das glaube ich nicht.
| as_string hat Folgendes geschrieben: | | Mal abgesehen davon, dass es für diese Aufgabe ein ziemlich umständlicher Weg wäre, würde Mathology da sicher nicht von selbst drauf kommen können. |
Da bin ich vollkommen Deiner Meinung. Mein Kommentar sollte nur darauf hinweisen, dass Derfnam das so gemeint haben könnte, wie ich es erläutert habe. Diese Erläuterung hätte natürlich von Derfnam kommen müssen. Was die Lern- oder Erkenntnisfähigkeit von Mathology angeht, möchte ich lieber keinen Kommentar abgeben.
| as_string hat Folgendes geschrieben: | Ich hätte es ok gefunden, wenn er noch dazu geschrieben hätte, dass bei diesem Ansatz die Eigengewichte der Federn noch nicht berücksichtigt ist und man diese getrennt berechnen und addieren kann. Aber sonst ist es einfach im besten Fall verwirrend und im schlechtesten irreführend.
|
Genau.
|
|
 |
Derfnam
Gast
|
 Derfnam Verfasst am: 18. Apr 2017 17:31 Titel: Derfnam Verfasst am: 18. Apr 2017 17:31 Titel: |
 |
|
[quote="GvC"] | as_string hat Folgendes geschrieben: |
Ja, der Ton gerät bei solchen Diskussionen zuweilen aus dem Gleis. Mit mir hat Derfnam das auch schon gemacht.
|
Der Zusammenhang zwischen Ursache u. Wirkung ist aber schon bekannt, oder?
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 18. Apr 2017 19:08 Titel: as_string Verfasst am: 18. Apr 2017 19:08 Titel: |
 |
|
| Derfnam hat Folgendes geschrieben: | | Der Zusammenhang zwischen Ursache u. Wirkung ist aber schon bekannt, oder? |
Du meinst "der hat aber angefangen" oder wie?
Dann geh doch den Thread mal bitte durch (oder auch andere) und sage mir bitte, an welcher Stelle ich zu Dir unfreundlich war oder was Dir "quer gelegen" ist, bevor Du mir vorgeworfen hast, ich hätte immer was zu "klötern ohne selbst konkret etwas zu posten"! Ich empfand auf jeden Fall diese Aussage von Dir als ziemlich beleidigend (Du kannst ja mal schauen, was ich in den letzten Jahren so alles gepostet habe hier und dann nochmal überlegen, ob Deine Aussage mit "nichts konkretes" so zu halten ist) und mir ist beim besten Willen nicht klar, an welcher Stelle ich Dir gegenüber vorher beleidigend gewesen wäre.
Falls Du Korrekturen oder zumindest Ergänzungen als eine Beleidigung auffasst, dann liegt der Fehler jeden Falls eindeutig bei Dir. Denke mal darüber nach!
Gruß
Marco
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 18. Apr 2017 19:13 Titel: GvC Verfasst am: 18. Apr 2017 19:13 Titel: |
 |
|
Hallo Marco,
Derfnam meint nicht Dich, sondern mich. Das ist wegen seiner mangelhaften Zitierfähigkeit allerdings nicht sofort zu erkennen.
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 18. Apr 2017 20:07 Titel: VeryApe Verfasst am: 18. Apr 2017 20:07 Titel: |
 |
|
was ist da in letzter Zeit immer los.
Kann hier überhaupt keiner mehr Kritik vertragen.
Jeder ist sofort beleidigt, wenn ihm einer mal sagt, so funktioniert es nicht.
Das gute daran ist doch das hier etliche Leute was auf den Kasten haben und ihren Senf dazugeben. Keiner kann alles wissen und wenn einer Fehler reinhaut dann kommen die anderen und besseren ihn aus, was ist da schlecht daran.
JEtzt hat Derfnam mit seiner Lösung daneben gehauen, das nächste Mal passts wieder.
Mir kommts in letzter Zeit vor da gehts um einen HAufen Geld. Pro Lösung klingelt die Kasse.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 19. Apr 2017 12:45 Titel: Mathefix Verfasst am: 19. Apr 2017 12:45 Titel: |
 |
|
|
Mein Ergebnis: 87,12 cm
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 19. Apr 2017 13:11 Titel: GvC Verfasst am: 19. Apr 2017 13:11 Titel: |
 |
|
| Mathefix hat Folgendes geschrieben: | | Mein Ergebnis: 87,12 cm |
Mal abgesehen von einem kleinen Rundungsfehler ist das richtig.
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 19. Apr 2017 13:39 Titel: Mathefix Verfasst am: 19. Apr 2017 13:39 Titel: |
 |
|
| GvC hat Folgendes geschrieben: | | Mathefix hat Folgendes geschrieben: | | Mein Ergebnis: 87,12 cm |
Mal abgesehen von einem kleinen Rundungsfehler ist das richtig. |
Du hast recht. Muss 12,17 heissen.
Lt. Aufgabenstellung war eindeutig klar, dass das Eigengewicht der Federn zu berücksichtigen war - wozu sonst die deren Angabe.
Wozu das ganze Bohei?
|
|
 |
Mathology
Anmeldungsdatum: 18.10.2013
Beiträge: 415
|
 Mathology Verfasst am: 19. Apr 2017 14:41 Titel: Mathology Verfasst am: 19. Apr 2017 14:41 Titel: |
 |
|
tut mir leid ich hatte die letzten Tage keine Zeit zum lernen! Bin aber die kommenden Tage hoffentlich bald wieder da.  
|
|
 |
Derfnam
Gast
|
 Derfnam Verfasst am: 20. Apr 2017 10:45 Titel: Derfnam Verfasst am: 20. Apr 2017 10:45 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: |
JEtzt hat Derfnam mit seiner Lösung daneben gehauen, das nächste Mal passts wieder.
|
Aber nur in Bezug auf die Einfederung durch Eigengewicht.
Die Federschaltungen selbst stehen so in jedem Lehrbuch. Da ist also nichts Falsches oder Verwirrendes.
Ich hoffe, ich habe jetzt richtig zitiert. Bei nur 20% Sehkraft auf einem Auge ist das für mich manchmal schwierig zu erkennen.
|
|
 |
Mathology
Anmeldungsdatum: 18.10.2013
Beiträge: 415
|
 Mathology Verfasst am: 20. Apr 2017 14:58 Titel: Mathology Verfasst am: 20. Apr 2017 14:58 Titel: |
 |
|
Also: | Zitat: | | überlege Dir zuerst, welche Kräfte die untere Feder dehnt. Das ist die Gewichtskraft der angehängten Masse plus nach Huggys Rechnung die Hälfte der Gewichtskraft der Feder selbst. Das kannst Du in das Hooke'sche Gesetz einsetzen und hast die Verlängerung der unteren Feder. |
Untere Feder : 1,5 N (Massestück Gewichtskraft) + 0,1 (Hälfte der Gewichtskraft der Feder) sind 1,6N
Dann in das Hooksche Gesetz
s=F/D = 1,6 N / 0,08 N_cm = 20cm
DANN: | Zitat: | | Für die obere Feder addierst Du wieder die Gewichtskräfte von dem was unten dran hängt, also die von der Masse plus der unteren Feder. Dann wieder die Hälfte der oberen Feder dazu und ins Hooke'sche Gesetz damit. |
1,5 N (Masse) + 0,2 N (untere Feder) + 0,125 N (Hälfte der Oberen Feder) = 1,825 N
Dann in das Hook'sche Gesetz
s= F/D = 1,825 N/ 0,15 N_cm = 12,17 cm
Also kommt dann daraus insgesamt: 20cm+35cm+20cm+12,17cm = 87,17 cm
So das wäre dann Richtig?
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 20. Apr 2017 18:34 Titel: Mathefix Verfasst am: 20. Apr 2017 18:34 Titel: |
 |
|
| Mathology hat Folgendes geschrieben: | Also: | Zitat: | | überlege Dir zuerst, welche Kräfte die untere Feder dehnt. Das ist die Gewichtskraft der angehängten Masse plus nach Huggys Rechnung die Hälfte der Gewichtskraft der Feder selbst. Das kannst Du in das Hooke'sche Gesetz einsetzen und hast die Verlängerung der unteren Feder. |
Untere Feder : 1,5 N (Massestück Gewichtskraft) + 0,1 (Hälfte der Gewichtskraft der Feder) sind 1,6N
Dann in das Hooksche Gesetz
s=F/D = 1,6 N / 0,08 N_cm = 20cm
DANN: | Zitat: | | Für die obere Feder addierst Du wieder die Gewichtskräfte von dem was unten dran hängt, also die von der Masse plus der unteren Feder. Dann wieder die Hälfte der oberen Feder dazu und ins Hooke'sche Gesetz damit. |
1,5 N (Masse) + 0,2 N (untere Feder) + 0,125 N (Hälfte der Oberen Feder) = 1,825 N
Dann in das Hook'sche Gesetz
s= F/D = 1,825 N/ 0,15 N_cm = 12,17 cm
Also kommt dann daraus insgesamt: 20cm+35cm+20cm+12,17cm = 87,17 cm
So das wäre dann Richtig? |
JA!
PS
Hast Du auch verstanden, warum die Gewichtskraft des Eigengewichts zur Hälfte in die Dehnung eingeht?
|
|
 |
Mathology
Anmeldungsdatum: 18.10.2013
Beiträge: 415
|
 Mathology Verfasst am: 21. Apr 2017 12:02 Titel: Mathology Verfasst am: 21. Apr 2017 12:02 Titel: |
 |
|
Also wenn ich ehrlich bin nein. Weil ich nicht verstehen wieso die hälfte und nicht das ganze.
Ich weiß das Huggy die Stammfunktion gebildet hat aber rein logisch kann ich die Hälfte in der Formel nicht nachvollziehen. Bzw verstehe nicht den Sinn.
|
|
 |
Derfnam
Gast
|
 Derfnam Verfasst am: 21. Apr 2017 13:38 Titel: Derfnam Verfasst am: 21. Apr 2017 13:38 Titel: |
 |
|
| GvC hat Folgendes geschrieben: | Hallo Marco,
Derfnam meint nicht Dich, sondern mich. Das ist wegen seiner mangelhaften Zitierfähigkeit allerdings nicht sofort zu erkennen. |
Mangelhaft!
Der Herr Lehrer verteilt Schulnoten, ohne in Erwägung zu ziehen, dass es auch andere (altersbedingte) Gründe geben könnte.
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 21. Apr 2017 13:54 Titel: Mathefix Verfasst am: 21. Apr 2017 13:54 Titel: |
 |
|
| Mathology hat Folgendes geschrieben: | Also wenn ich ehrlich bin nein. Weil ich nicht verstehen wieso die hälfte und nicht das ganze.
Ich weiß das Huggy die Stammfunktion gebildet hat aber rein logisch kann ich die Hälfte in der Formel nicht nachvollziehen. Bzw verstehe nicht den Sinn. |
Also, ich versuche es Dir zu erklären:
L = Länge der Feder
m_0 = Masse der Feder
G = Gewichtskraft der Feder
D = Federkonstante
Die Feder ist senkrecht aufgehängt. Die Masse der Feder nimmt vom freien, unteren Ende bis zum Aufhängepunkt bis zu ihrer Länge L linear mit x zu
 =\frac{m_0}{L} \cdot x)
und damit die Gewichtskraft G
 =\frac{m_0}{L}\cdot g \cdot x )
ein infinitesimales Stück dx hat den Längenanteil dx/L und damit die Gewichtskraft
\cdot \frac{dx}{L} = \frac{m_0}{L}\cdot g \cdot x \cdot \frac{dx}{L})
Für die Auslenkung einer Feder gilt:

Infinitesimale Änderung der Auslenkung
 =\frac{dG}{D} )
und
 = \frac{m_0\cdot g}{D\cdot L^{2} } \cdot x\cdot dx)
und die gesamte Auslenkung


Zuletzt bearbeitet von Mathefix am 21. Apr 2017 16:09, insgesamt 6-mal bearbeitet |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 21. Apr 2017 14:01 Titel: GvC Verfasst am: 21. Apr 2017 14:01 Titel: |
 |
|
| Derfnam hat Folgendes geschrieben: | | Der Herr Lehrer verteilt Schulnoten ... |
Bevor ich Lehrer geworden wäre, hätte ich mich lieber umgebracht.
Ich weiß gar nicht, was Du hast. Es ist eine Tatsache, dass Du vielfach falsch (=mangelhaft) zitierst und deshalb nicht klar wird, wen Du gerade angreifst. Dass das seine altersbedingten Gründe hat, mag ja sein. Aber erstens war das bis vor Kurzem nicht bekannt, und zweitens wollte ich ja nur die Stoßrichtung Deines Angriffs, den as_string auf sich bezogen hatte, auf mich umlenken. Denn in meine Richtung sollte der Angriff ja gehen. Oder hattest Du doch as_string gemeint?
|
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 21. Apr 2017 14:12 Titel: Huggy Verfasst am: 21. Apr 2017 14:12 Titel: |
 |
|
@Mathology
Ich versuche es mal sehr elementar und ganz ausführlich zu erklären. Die Notation folgt meinem ersten Beitrag in diesem Thread.
Für die Längenänderung der Feder mit der Länge 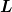 unter der Kraft unter der Kraft  gilt: gilt:

Die Dehnung  der Feder ist dann: der Feder ist dann:

Wen man nun eine gleichartige Feder mit einer anderen Länge 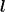 betrachtet, so hat diese zwar eine andere Längenänderung, aber die gleiche Dehnung. Es ist also: betrachtet, so hat diese zwar eine andere Längenänderung, aber die gleiche Dehnung. Es ist also:


Nun unterteilen wir die gegebene Feder in Teilstücke der Länge 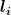 . Die gesamte Längenänderung ist dann die Summe der Längenänderungen der Teilstücke: . Die gesamte Längenänderung ist dann die Summe der Längenänderungen der Teilstücke:

Dabei ist  die auf das Teilstück mit der Nummer die auf das Teilstück mit der Nummer 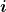 wirkende Kraft. Wenn man die Längenänderung unter dem Eigengewicht betrachtet, ist wirkende Kraft. Wenn man die Längenänderung unter dem Eigengewicht betrachtet, ist

wobei 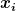 der Abstand des Teilstücks mit der Nummer der Abstand des Teilstücks mit der Nummer 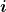 vom unteren Ende ist. Das ergibt: vom unteren Ende ist. Das ergibt:

Die Länge des Teilstücks mit der Nummer 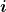 ist der Abstand zwischen aufeinanderfolgender ist der Abstand zwischen aufeinanderfolgender 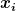 -Werten. Also: -Werten. Also:


Wenn man nun die Zahl der Teilstücke gegen unendlich und ihre Länge gegen Null gehen lässt, geht die Summe in ein Integral über

|
|
 |
|


















