| Autor |
Nachricht |
Erster Admiral
Anmeldungsdatum: 07.05.2021
Beiträge: 69
|
 Erster Admiral Verfasst am: 12. März 2022 15:20 Titel: Propagator eines einzelnen freien Teilchens |
 |
|
Laut https://core.ac.uk/download/pdf/230454912.pdf
ist der Propagator eines freien Teilchens (in einer Dimension), das durch die Schrödingergleichung determiniert wird gegeben durch:
=\sqrt{\frac{m}{2 \pi i \hbar T}}e^{im(x-x')/2 \hbar T}=\sqrt{\frac{m}{2 \pi \hbar T}}e^{-i \pi /4}e^{im(x-x')/2 \hbar T}) .
Das Betragsquadrat dieses Propagators gibt bekanntlich die Wahrscheinlichkeit an, dass sich das Teilchen in der Zeit T von x nach x' bewegt.
|^2=\frac{m}{2 \pi \hbar T} )
Wie kann es sein, dass diese Wahrscheinlichkeit nicht von der Distanz x-x' abhängt?
Hängt es damit zusammen, dass ein freies Teilchen nicht lokalisiert ist und die Wellenfunktion über den gesamten Raum ausgebreitet ist?
Warum nimmt diese Wahrscheinlichkeit mit zunehmendem T ab? |
|
 |
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18078
|
| TomS Verfasst am: 13. März 2022 05:50 Titel: Re: Propagator eines einzelnen freien Teilchens |
|
|
| Erster Admiral hat Folgendes geschrieben: | Laut https://core.ac.uk/download/pdf/230454912.pdf
ist der Propagator eines freien Teilchens (in einer Dimension), das durch die Schrödingergleichung determiniert wird gegeben durch:
. |
Die Form für dein U - üblicherweise immer K - passt nicht ganz; man erhält
^2/2 \hbar T}) .
| Erster Admiral hat Folgendes geschrieben: | | Das Betragsquadrat dieses Propagators gibt bekanntlich die Wahrscheinlichkeit an, dass sich das Teilchen in der Zeit T von x nach x' bewegt. |
Eine Interpretation des Betragsquadrats kenne ich so nicht.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Erster Admiral
Anmeldungsdatum: 07.05.2021
Beiträge: 69
|
| Erster Admiral Verfasst am: 13. März 2022 11:21 Titel: Re: Propagator eines einzelnen freien Teilchens |
|
|
| TomS hat Folgendes geschrieben: |
Eine Interpretation des Betragsquadrats kenne ich so nicht. |
"Der Propagator liefert die Wahrscheinlichkeitsamplitude, ein zum Zeitpunkt t_0 bei x_0 lokalisiertes Teilchen zum Zeitpunkt t bei x zu finden."
- Wikipedia
https://de.wikipedia.org/wiki/Propagator |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 13. März 2022 12:56 Titel: Re: Propagator eines einzelnen freien Teilchens |
|
|
| Erster Admiral hat Folgendes geschrieben: | Laut https://core.ac.uk/download/pdf/230454912.pdf
ist der Propagator eines freien Teilchens (in einer Dimension), das durch die Schrödingergleichung determiniert wird gegeben durch:
.
Das Betragsquadrat dieses Propagators gibt bekanntlich die Wahrscheinlichkeit an, dass sich das Teilchen in der Zeit T von x nach x' bewegt.
Wie kann es sein, dass diese Wahrscheinlichkeit nicht von der Distanz x-x' abhängt?
|
Es wäre |^2) die Wahrscheinlichkeitsdichte für den Aufenthaltsort x zur Zeit T, wenn das Teilchen ursprünglich bei x' lokalisiert war. Daß man das hier nicht so wörtlich nehmen kann, liegt einfach daran, daß die beteiligten Amplituden nicht normierbar sind. Die Betragsquadrate solcher verallgemeinerten Zustände kann man nicht als punktweise definierte Wahrscheinlichkeitsdichten auffassen. Das geht erst, wenn du ) mit einer normierbaren Wellenfunktion  faltest. Wenn du für einfach eine schmale Gaußfunktion und keine Deltafunktion vorwendest, dann definiert
 = \int \dd x' U(x, x', T)\psi_0(x'))
auch eine vernünftige Dichte |^2) zur Zeit T, und sie fällt für festes T auch mit dem Abstand ab.
| Zitat: |
Hängt es damit zusammen, dass ein freies Teilchen nicht lokalisiert ist und die Wellenfunktion über den gesamten Raum ausgebreitet ist?
|
Ja. Ein freies Teilchen kann zwar schon lokalisiert sein. Es delokalisiert aber um so schneller, je stärker es anfänglich lokalisiert ist. Der Extremfall ist natürlich wieder durch die initiale Deltafunktion gegeben.
| Zitat: |
Warum nimmt diese Wahrscheinlichkeit mit zunehmendem T ab? |
Für eine normierbare Wellenfunktion nimmt ja auch die Breite zu. Für den verallgemeinerten Zustand U(x, x', T) selbst ist der Wert der Amplitude eigentlich unerheblich. Die Norm ist ohnehin unendlich, also spielt der Wert eines endlichen Normierungsfaktors keine Rolle mehr.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 13. März 2022 15:12 Titel: Re: Propagator eines einzelnen freien Teilchens |
|
|
| Erster Admiral hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: |
Eine Interpretation des Betragsquadrats kenne ich so nicht. |
"Der Propagator liefert die Wahrscheinlichkeitsamplitude, ein zum Zeitpunkt t_0 bei x_0 lokalisiertes Teilchen zum Zeitpunkt t bei x zu finden."
- Wikipedia
https://de.wikipedia.org/wiki/Propagator |
Ja, das ist nur ein Spezialfall der Bornschen Regel bzw. der statistischen Interpretation der Wellenfunktion. Man kann  = |\langle x |e^{-iHt}\psi\rangle|^2) als die bedingte Wahrscheinlichkeitsdichte für den Aufenthaltsort x zur Zeit t ansehen unter der Bedingung, daß 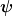 der Zustand zum Zeitpunkt t=0 war. Wenn dieser Initialzustand der Ortseigenzustand  war, dann landet man bei =|\langle x|e^{-iHt}|x'\rangle|^2) , der Wahrscheinlichkeit für den Ort x bei t, wenn der Anfangsort x' war oder m.a.W. der Wahrscheinlichkeit, daß sich das Teilchen während der Zeit t von x' nach x bewegt hat. Das einzige Problem mit dieser Interpretation ist eben, daß die zugehörigen Amplituden singulär sind und keine vernünftigen Wahrscheinlichkeitsmaße definieren.
_________________
It is just this lack of connection to a concern with truth -- this indifference to how things really are -- that I regard as of the essence of bullshit. -- Harry G. Frankfurt |
|
|
Erster Admiral
Anmeldungsdatum: 07.05.2021
Beiträge: 69
|
| Erster Admiral Verfasst am: 17. März 2022 10:54 Titel: |
|
|
|
danke dir @index_razor das beantwortet meine Frage fürs erste. |
|
|
|
|
Registrieren
Login
FAQ
Suchen
