| Autor |
Nachricht |
Physik_Student
Anmeldungsdatum: 01.07.2021
Beiträge: 26
|
 Physik_Student Verfasst am: 05. Sep 2021 19:26 Titel: Potential, Drehimpulserhaltung |
 |
|
Meine Frage:
Hallo,
ich soll in einer Aufgabe verschiedene Potentiale auf Drehimpulserhaltung untersuchen. Leider komme ich nicht auf das, was in der Lösung steht...
Als Beispiel nehme ich das Potential:
 = \frac{1}{2}Dcos(\omega t)r^2)
Dabei ist r=(x,y,z).
Meine Ideen:
Für die Drehimpulserhaltung habe ich 2 Kriterien gefunden: einmal Rotationsinvarianz und einmal Isotropie des Raumes. Um die Isotropie des Raumes zu zeigen, habe ich die partiellen Ableitungen gebildet, weil ich dachte, wenn die partiellen Ableitungen in alle Richtungen gleich sind, dann ist der Raum Isotrop und somit gilt Drehimpulserhaltung in alle Raumrichtungen.
Es gilt:
x)
y)
z)
In der Lösung steht, dass bei diesem Potential die Drehimpulserhaltung nur um die Achse erhalten ist, die durch den Ursprung geht. Mir ist nicht ganz klar, wie man darauf anhand der partiellen Ableitungen kommt. Ist mein Ansatz einfach falsch? Denn natürlich, für x=y=z=0 wäre der Raum isotrop, aber nach dieser Logik müsste ich für andere Potentiale aus der Aufgabe auch dieses Ergebnis bekommen und das ist nicht so. Kann mir jemand helfen?
Danke im Voraus! |
|
 |
curious
Gast
|
| curious Verfasst am: 06. Sep 2021 09:01 Titel: Re: Potential, Drehimpulserhaltung |
|
|
| Physik_Student hat Folgendes geschrieben: | Meine Frage:
Hallo,
ich soll in einer Aufgabe verschiedene Potentiale auf Drehimpulserhaltung untersuchen. Leider komme ich nicht auf das, was in der Lösung steht...
Als Beispiel nehme ich das Potential:
Dabei ist r=(x,y,z).
Meine Ideen:
Für die Drehimpulserhaltung habe ich 2 Kriterien gefunden: einmal Rotationsinvarianz und einmal Isotropie des Raumes. Um die Isotropie des Raumes zu zeigen, habe ich die partiellen Ableitungen gebildet, weil ich dachte, wenn die partiellen Ableitungen in alle Richtungen gleich sind, dann ist der Raum Isotrop und somit gilt Drehimpulserhaltung in alle Raumrichtungen.
Es gilt:
In der Lösung steht, dass bei diesem Potential die Drehimpulserhaltung nur um die Achse erhalten ist, die durch den Ursprung geht. Mir ist nicht ganz klar, wie man darauf anhand der partiellen Ableitungen kommt. |
die Ableitungen hängen doch noch von x, y und z ab?
D.h. das Potential, dass Du siehst, wenn Du z.B. in negative x-Richtung schaust, sieht anders aus, als das, wenn Du in positive x-Richtung schaust.
Solange Du Dich auf einer Kugelschale um den Ursprung bewegst, bleibt das gleich. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 06. Sep 2021 11:24 Titel: |
|
|
Komisch, Nachrechnen liefert einfach einen erhaltenen Drehimpuls:
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 06. Sep 2021 13:06, insgesamt einmal bearbeitet |
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
| DrStupid Verfasst am: 06. Sep 2021 12:47 Titel: Re: Potential, Drehimpulserhaltung |
|
|
| Physik_Student hat Folgendes geschrieben: | | In der Lösung steht, dass bei diesem Potential die Drehimpulserhaltung nur um die Achse erhalten ist, die durch den Ursprung geht. |
Heißt das nicht einfach, dass die Bezugssysteme, mit denen das Potential und der Drehimpuls formuliert werden, den gleichen Ursprung haben? Das würde ich für selbstverständlich halten. Wenn man nur eines von beiden verschiebt und dann blind mit den jeweiligen Koordinaten weiterrechnet, dann ist der Drehimpuls natürlich nicht mehr erhalten. Aber warum sollte man das tun?
Zuletzt bearbeitet von DrStupid am 06. Sep 2021 16:51, insgesamt einmal bearbeitet |
|
|
Physik_Student
Anmeldungsdatum: 01.07.2021
Beiträge: 26
|
| Physik_Student Verfasst am: 06. Sep 2021 13:37 Titel: |
|
|
Hallo,
ich hätte dazu zwei Fragen:
| Zitat: |
|
Wie kommt man auf  ? Das ist ja das Trägheitsmoment, oder?
| Zitat: |
|
Wieso ist  ? Liegt das daran, dass das hier ein Zentralkraftpotential ist und somit die Beschleunigung zum Ursprung zeigt? |
|
|
Physik_Student
Anmeldungsdatum: 01.07.2021
Beiträge: 26
|
| Physik_Student Verfasst am: 06. Sep 2021 13:43 Titel: Re: Potential, Drehimpulserhaltung |
|
|
| Zitat: |
D.h. das Potential, dass Du siehst, wenn Du z.B. in negative x-Richtung schaust, sieht anders aus, als das, wenn Du in positive x-Richtung schaust. |
ja, das ergibt Sinn
| Zitat: |
Solange Du Dich auf einer Kugelschale um den Ursprung bewegst, bleibt das gleich. |
Das verstehe ich nicht wirklich, warum bleibt es gleich, wenn ich mich auf einer Kugelschale um den Ursprung bewege? Dabei ändern sich doch auch die Werte von negativ nach positiv usw.? |
|
|
schnudl
Moderator
Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
| schnudl Verfasst am: 06. Sep 2021 14:30 Titel: |
|
|
| Physik_Student hat Folgendes geschrieben: |
Wieso ist ? Liegt das daran, dass das hier ein Zentralkraftpotential ist und somit die Beschleunigung zum Ursprung zeigt? |
Ja, genau. Die Beschleunigung, also die Kraft zeigt in die selbe Richtung wie r.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 06. Sep 2021 14:47 Titel: |
|
|
| Physik_Student hat Folgendes geschrieben: | | Zitat: |
|
Wie kommt man auf ? Das ist ja das Trägheitsmoment, oder? |
Na ja, J ist nur ein Buchstabe. Wenn ich für den Drehimpuls L verwendet hätte, dann hättest du geschrieben, dass L doch die von mir definierte Lagrangefunktion ist ;-)
J bezeichnet den Drehimpuls, das wird durch den rechts stehenden Term, der letztlich die Definition des Drehimpulses darstellt, doch klar.
| Physik_Student hat Folgendes geschrieben: | | Zitat: |
|
Wieso ist ? Liegt das daran, dass das hier ein Zentralkraftpotential ist und somit die Beschleunigung zum Ursprung zeigt? |
Ja.
Mit der o.g. Bewegungsgleichung
und der Zeitableitung des Drehimpulses
 = \dot{\vec{r}} \times \dot{\vec{r}} + {\vec{r}} \times \ddot{\vec{r}})
verschwindet der zweite Term
Der erste ist ohnehin Null.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Physik_Student
Anmeldungsdatum: 01.07.2021
Beiträge: 26
|
| Physik_Student Verfasst am: 06. Sep 2021 15:44 Titel: |
|
|
| Zitat: |
J bezeichnet den Drehimpuls, das wird durch den rechts stehenden Term, der letztlich die Definition des Drehimpulses darstellt, doch klar. |
Ja stimmt, ich war verwirrt, weil das m vor dem r steht, aber einen Skalar kann man ja im Kreuzprodukt verschieben.
Aber dann ist jetzt immer noch die Frage, wieso die Lösung eine andere ist... |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 06. Sep 2021 15:56 Titel: Re: Potential, Drehimpulserhaltung |
|
|
| Physik_Student hat Folgendes geschrieben: | | In der Lösung steht, dass bei diesem Potential die Drehimpulserhaltung nur um die Achse erhalten ist, die durch den Ursprung geht. |
Das ist mir nicht klar.
Der Drehimpuls ist erhalten, auch wenn überhaupt keine Rotation um eine Achse vorliegt. Z.B. ist der Drehimpuls eines freien, geradlinig bewegten Teilchens erhalten, ohne dass es um eine Achse rotiert.
Außerdem ist die von mir verwendete Definition des Drehimpulses koordinatenfrei, d.h. unabhängig von Koordinatenachsen formuliert.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
| DrStupid Verfasst am: 06. Sep 2021 17:01 Titel: |
|
|
| Physik_Student hat Folgendes geschrieben: | | Aber dann ist jetzt immer noch die Frage, wieso die Lösung eine andere ist... |
Ich vermute (wier oben schon gesagt), dass sich diese Aussage auf verschiedene Bezugssysteme bezieht. Für eine Translation des Bezugssystems gilt gemäß Galilei-Transformation
Wenn man jetzt beim Potential mit den Kordinaten von r und beim Drehimpuls mit denen von r' rechnet (oder umgekehrt), dann kommt man zu einem anderen Resultat. Das macht zwar keinen Sinn, aber das ist die einzige Idee, die ich habe. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 06. Sep 2021 17:13 Titel: |
|
|
Aber das ergibt doch nie Sinn, nicht nur in diesem Fall.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5852
|
| Myon Verfasst am: 06. Sep 2021 17:27 Titel: |
|
|
|
Vielleicht ist einfach gemeint, dass der Drehimpuls bez. des Ursprungs als Bezugspunkt oder bezüglich einer beliebigen Achse durch den Ursprung erhalten bleibt. Für den Drehimpuls bezüglich eines anderen Punktes im Raum (oder bei einem ausgedehnten Körper z.B. bez. dessen Schwerpunkts) gilt das nicht. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 06. Sep 2021 17:45 Titel: |
|
|
Wenn du dir die Definition des Drehimpulses anschaust, dann stellst du fest, dass dies immer der Fall ist - mit Ausnahme des freien Teilchens. Das liegt an der fehlenden Homogenität, d.h. dass eine zeitunabhängige Translation
 \to \vec{r}_a(t) = \vec{r}(t) + \vec{a} )
eine Lösung nicht in eine andere Lösung überführt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
| DrStupid Verfasst am: 06. Sep 2021 18:34 Titel: |
|
|
| Myon hat Folgendes geschrieben: | | Vielleicht ist einfach gemeint, dass der Drehimpuls bez. des Ursprungs als Bezugspunkt oder bezüglich einer beliebigen Achse durch den Ursprung erhalten bleibt. |
Was genau heißt denn "Drehimpuls bez. des Ursprungs als Bezugspunkt oder bezüglich einer beliebigen Achse"? |
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5852
|
| Myon Verfasst am: 07. Sep 2021 08:57 Titel: |
|
|
Ich sehe schon, dass es eigentlich klar ist, dass die Drehimpulserhaltung nur bez. des Ursprungs gilt. Ich dachte aber, dass vielleicht doch dies in der Lösung gemeint war, dass die Drehimpulserhaltung nur bezüglich eines bestimmten Punktes gilt.
| DrStupid hat Folgendes geschrieben: | | Was genau heißt denn "Drehimpuls bez. des Ursprungs als Bezugspunkt oder bezüglich einer beliebigen Achse"? |
Der Drehimpuls bez. eines Punktes r0 ist
\times\vec{p})
Mit dem Drehimpuls bezüglich einer bestimmten Achse 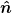 meinte ich einfach
 |
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
| DrStupid Verfasst am: 07. Sep 2021 09:06 Titel: |
|
|
| Myon hat Folgendes geschrieben: | Der Drehimpuls bez. eines Punktes r0 ist
|
Ist das offiziell? Ich kenne den Drehimpuls nur als Kreuzprodukt aus Ortsvektor und Impuls. Was Du als Drehimpuls bez. eines Punktes r0 bezeichnest ist dann der Drehimpuls in einem Bezugssystem mit Ursprung in r0. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 07. Sep 2021 09:27 Titel: |
|
|
| DrStupid hat Folgendes geschrieben: | | Myon hat Folgendes geschrieben: | Der Drehimpuls bez. eines Punktes r0 ist
|
Ist das offiziell? |
Ja, man kann das in einem affinen Raum genau so definieren. Wenn das entsprechend eingeführt wurde, dann ist es natürlich zulässig, vom allgemeinen Fall zu diesem Spezialfall überzugehen.
Ich halte es jedoch für eine mathematische Spitzfindigkeit. Interessanter ist die Frage, was es physikalisch bedeutet. Dazu siehe oben: Die Translation einer Bahnkurve als Lösung der Bewegungsgleichung führt nicht auf eine neue Lösung. Formal ist das natürlich der selbe Ausdruck, aber es ist physikalisch klarer als „Drehimpuls bzgl. eines Punktes“, insbs. wenn sich nichts wirklich um diesen Punkt dreht.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
| DrStupid Verfasst am: 07. Sep 2021 09:40 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | Ich halte es jedoch für eine mathematische Spitzfindigkeit. |
Wenn man in einem Bezugssystem verschiedene Drehimpulse definieren kann, die sich jeweils auf verschiedene Punkte beziehen, dann ist es hier sinnvoll die Drehimpulserhaltung auf denjenigen Drehimpuls zu beschränken, der sich auf den Ursprung bezieht. Wenn es sich aber um denselben Drehimpuls in unterschiedlichen Bezugssystemen handelt, dann muss man das Potential vernünftigerweise mittransformieren und dann ist der Drehimpuls bei einem Zentralpotential immer erhalten. Ich denke das ist mehr als nur eine mathematische Spitzfindigkeit. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 07. Sep 2021 10:19 Titel: |
|
|
Zunächst mal hat nichts mit einer Koordinatentransfornation zu tun; das Potential wird nicht mittransformiert.
Ja, wenn du so willst, dann handelt es sich tatsächlich um unterschiedliche Drehimpulse
 \times p)
bzgl. verschiedener Punkte a. Ich halte das deswegen für künstlich, weil diese Drehimpulse nur dann alle erhalten sind, wenn ein freies Teilchen vorliegt. Ansonsten ist das nicht der Fall, d.h. wir würden unendlich viele Größen einführen, nur um sie dann - mit Ausnahme einer einzigen - wieder zu verwerfen. Wenn es nicht unnatürlich wäre, würde uns das ja auch ständig über den Weg laufen.
Ich halte es für einfacher, schlicht festzustellen, dass für eine Bahnkurve
 )
die die oben diskutierte Bewegungsgleichung löst, die Translation
 + a )
keine neue Lösung der Bewegungsgleichung liefert.
Natürlich liefert das die selbe mathematische Formel, aber eine physikalisch andere Argumentation: Aufgrund der fehlenden Homogenität ist die Translation keine Symmetrie des Problems; man erkennt, dass für eine Lösung
gilt, d.h. die Erhaltung von J_a scheitert an der Impulserhaltung. Das sollte man aber m.E. nicht mit der Drehimpulserhaltung vermischen.
Evtl. kann man sich das mal für untereinander wechselwirkende Teilchen ohne äußeres Potential ansehen; vlt. sieht man dann einen tieferen Sinn in der Einführung der Größen J_a.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
|
Registrieren
Login
FAQ
Suchen
