| Autor |
Nachricht |
WebFritzi
Anmeldungsdatum: 07.02.2008
Beiträge: 13
|
 WebFritzi Verfasst am: 13. Jul 2021 00:49 Titel: Prinzip der stationären Wirkung |
 |
|
Hallo @all.
Ich bin Mathematiker, kein Physiker, versuche aber gerade das Prinzip der stationären Wirkung in konservativen Systemen zu verstehen. Ich weiß, dass es sowohl äquivalent ist zu den Euler-Lagrange-Gleichungen (ELG) als auch zu den Hamiltonischen Gleichungen. Eine Erklärung für eines dieser drei Prinzipien würde mir reichen. Im Falle eines Teilchens in einem Kraftfeld habe ich die ELG mathematisch bestätigen können, mir fehlt jedoch jegliche Intuition. Ich frage mich auch, welchen Sinn es macht, dass  ist, also die Differenz. Steckt da auch irgend eine Intuition dahinter?
Ein mechanisches System heißt ja konservativ, wenn die Gesamtkraft (in verallg. Koordinaten) ein Potential 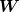 besitzt. Man kann dann zeigen, dass die Gesamtenergie  auf Lösungen der ELG konstant bleibt. Super, denn genau das erwartet man ja von einem konservativen System. Aber ist auch die Umkehrung korrekt? Sprich: Folgt aus der Konstanz von 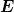 auf allen zulässigen Bahnen des Systems, dass diese den ELG genügen? Ich kann zeigen, dass aus ,\dot q(t)) = 0) folgt, dass \dot q = 0) , aber nicht mehr. |
|
 |
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18074
|
| TomS Verfasst am: 13. Jul 2021 07:57 Titel: |
|
|
Man kann diese Prinzipen physikalisch lediglich motivieren, nicht beweisen. Sie führen in einfachen Fällen auf bekannte Gleichungen aus der Newtonschen Mechanik, sind jedoch einfacher verallgemeinerbar als diese.
Physikalisch anschaulicher ist teilweise der Hamiltonsche Formalismus, da H mit der erhaltenen Energie E identifiziert werden kann. Umgekehrt ist jedoch die Identifizierung von Erhaltungsgrößen in der Lagrangeschen Formulierung aufgrund des Noetherschen Theorems meist einfacher. Beide Ansätze haben also ihre Berechtigung.
Zu deiner letzten Frage: L und H gehen mittels Legendre-Transformation aus einander hervor. Wenn H bekannt ist, dann folgt zunächst L aus H mittels Legendre-Rücktransformation sowie anschließend E = const. aus L auf einer Lösung der Euler-Lagrange-Gleichungen mittels Translationsinvarianz in der Zeit und Noether-Theorem. Umgekehrt folgt wieder H aus L mittels Legendre-Transformation sowie H = const. auf einer Lösung der Hamiltonschen Gleichungen mittels {H,H} = 0.
Der einzige offene Punkt ist, ob und unter welchen Bedingungen H auf einer Lösung der Hamiltonschen Gleichungen mit E = const. identifiziert werden kann. Ich sehe spontan keinen allgemeingültigen Beweis.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
gast_free
Gast
|
| gast_free Verfasst am: 13. Jul 2021 10:55 Titel: |
|
|
Für mich stellt dieser Formalismus eine elegante Methode dar, die Bewegungsleichungen für klassische mechanische Systeme herzuleiten. Man hat nur eine Gleichung, die die gesamte klassische Mechanik beschreibt. Hierzu wird die Lagrange Funktion und die generalisierten Koordinaten eingeführt, die die Zwangsbedingungen gleich mit berücksichtigen.
Diese Beschreibung bleibt auch in beschleunigten Bezugssystemen gültig und ist invariant gegenüber Koordinatentransformationen. Des weiteren ermöglicht dieser Formalismus das Erkennen von Erhaltungsgrößen (Noether Theorem).
Worauf allerdings das Hamiltonsche Prinzip der extremalen Wirkung zurück zu führen ist, bleibt mir unklar. Ich halte es für eine Beschreibung die sich bewährt hat und nicht im Widerspruch z.B. zu den Newtonschen Axiomen und anderen Beobachtungen steht. Die gedanklichen Grundlagen, auf denen die Theorie von Lagrange, Hamilton usw. aufbauen stammen wohl von Maupertius.
Mehr kann ich als einfacher Ingenieur nicht beitragen. |
|
|
WebFritzi
Anmeldungsdatum: 07.02.2008
Beiträge: 13
|
| WebFritzi Verfasst am: 13. Jul 2021 12:47 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | Man kann diese Prinzipen physikalisch lediglich motivieren, nicht beweisen. |
Das ist mir klar. Und genau um eine solche Motivation geht es mir. Es muss doch einen physikalischen Grund geben, warum das Wirkungsfunktional bei Lösungen stationär ist. Die Jungs werden das ja nicht einfach so hingeschrieben haben. Und nur, weil das Prinzip in vielen einfachen Fällen zutrifft, heißt es ja nicht, dass es nicht mal irgendwann schief geht.
| TomS hat Folgendes geschrieben: | | Physikalisch anschaulicher ist teilweise der Hamiltonsche Formalismus, da H mit der erhaltenen Energie E identifiziert werden kann. |
Ja, zumindest hat H eine physikalische Bedeutung, was man von L wohl nicht behaupten kann (?). Dennoch sind mir auch die Hamiltonischen Gleichungen physikalisch nicht klar.
| TomS hat Folgendes geschrieben: | | Umgekehrt ist jedoch die Identifizierung von Erhaltungsgrößen in der Lagrangeschen Formulierung aufgrund des Noetherschen Theorems meist einfacher. Beide Ansätze haben also ihre Berechtigung. |
Das verstehe ich nicht ganz. Ich dachte, das Noethersche Theorem ist bereits innerhalb des Hamiltonischen Formalismus formuliert.
| TomS hat Folgendes geschrieben: | | L und H gehen mittels Legendre-Transformation aus einander hervor. |
Das ist interessant. Schaue ich mir mal an.
| TomS hat Folgendes geschrieben: | | Umgekehrt folgt wieder H aus L mittels Legendre-Transformation sowie H = const. auf einer Lösung der Hamiltonschen Gleichungen mittels {H,H} = 0. |
In dem Zusammenhang habe ich folgende Frage: Sagen wir, das System ist zeitabhängig. Wir setzen dann ) und erhalten aus den Hamiltonischen Gleichungen:
) = \nabla H(x(t))^T\dot x(t) = (\frac{\partial H}{\partial q},\frac{\partial H}{\partial p},\frac{\partial H}{\partial t})\cdot(\frac{\partial H}{\partial p},-\frac{\partial H}{\partial q},1) = \frac{\partial H}{\partial t},)
was i.A. nicht Null ist. Da stimmt doch was nicht.
| TomS hat Folgendes geschrieben: | | Der einzige offene Punkt ist, ob und unter welchen Bedingungen H auf einer Lösung der Hamiltonschen Gleichungen mit E = const. identifiziert werden kann. Ich sehe spontan keinen allgemeingültigen Beweis. |
Ok. Aber mal davon abgesehen, sehe ich diese Frage nicht als "einzigen offenen Punkt". ;-) |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18074
|
| TomS Verfasst am: 13. Jul 2021 16:40 Titel: |
|
|
Die Motivation war m.W.n, mit einem universell gültigen und präzise formulierten Prinzip anstelle einiger loser Axiome nach Newton zu starten. Und das ist ja auch gelungen: wir können heute alle bekannten und etablierten Theorien aus einer geeigneten Wirkung ableiten.
Die genaue Form von L = T - V folgt dann aus der bekannten Form für E sowie der Forderung, dass die Newtonschen sowie die Euler-Lagrangeschen Bewegungsgleichungen übereinstimmen. Lass dich aber nicht von dieser Form von L irritieren, das ist lediglich ein Spezialfall.
Die Hamiltonischen Gleichungen entsprechen genau der Newtonschen Bewegungsgleichung für den Spezialfall dass p = mv sowie F = -dV/dx.
Man kann das Noethersche Theorem für den Hamiltonschen Formalismus geeignet umformulieren. Da Lagrangescher und Hamiltonscher Formalismus strikt äquivalent sind, ist dies auch nicht weiter verwunderlich. Ursprünglich formuliert wurde es jedoch für die Symmetrie der Wirkung S, und in dieser Form ist es oft wesentlich einfacher anzuwenden als für den Hamiltonian H.
Welche zentralen offenen Punkte siehst du denn außer
| TomS hat Folgendes geschrieben: | | ... ob und unter welchen Bedingungen H auf einer Lösung der Hamiltonschen Gleichungen mit E = const. identifiziert werden kann. |
noch?
(Lass' mal zeitabhängige Probleme weg; das machts unübersichtlich und ist nicht unbedingt zielführend; letztlich kann jedes offene System auch als Teil eines abgeschlossenes Systems betrachtet werden)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
WebFritzi
Anmeldungsdatum: 07.02.2008
Beiträge: 13
|
| WebFritzi Verfasst am: 13. Jul 2021 17:14 Titel: |
|
|
| Zitat: | | Die Motivation war m.W.n, mit einem universell gültigen und präzise formulierten Prinzip anstelle einiger loser Axiome nach Newton zu starten. |
Das ist eine Motivation, klar. Ich verstehe, dass das besonders vorteilhaft ist und begeistere mich etwas dafür. Deshalb ja auch meine Fragen
| Zitat: | | Die genaue Form von L = T - V folgt dann aus der bekannten Form für E sowie der Forderung, dass die Newtonschen sowie die Euler-Lagrangeschen Bewegungsgleichungen übereinstimmen. |
Die ELG folgen ja aus dem Prinzip der stat. Wirkung (PSW). Ok, und andersherum. Die Frage ist also, was die Henne ist und was das Ei. Für mich ist das PSW die Henne, die das Ei ELG legt. Man kennt die ELG also nicht, bevor man das PSW formuliert. Daher erkenne ich so nicht an, dass die Form von L aus der bekannten Form für E sowie der Forderung, dass die Newtonschen sowie die Euler-Lagrangeschen Bewegungsgleichungen übereinstimmen folgt. Was ich suche, ist eine physikalische Motivation/Erklärung dafür, dass die Wirkung für die physikalischen Bahnen stationär ist und warum man L so wählt, wie man es wählt (L = T - V).
Beispiel: Ein Ball hat eine gewisse Anfangsgeschwindigkeit, rollt einen Berg hinauf und dann wieder runter. Aufgabe: Erkenne anhand eines Zeit-Geschwindigkeit-Diagramms, wann der Ball am Gipfel ist. Lösung: Da wo die Geschwindigkeit minimal ist. Physikalische Begründung: Solange der Ball den Berg hinauf rollt, verliert er an Geschwindigkeit, und sobald er hinunter rollt, wird er beschleunigt und gewinnt wieder an Geschwindigkeit.
Eine solche Erklärung/Begründung hätte ich gerne für die Extremalität der Wirkung auf physikalischen Bahnen.
| Zitat: | | Lass dich aber nicht von dieser Form von L irritieren, das ist lediglich ein Spezialfall. |
??? Ich dachte, L ist immer die Differenz aus kinetischer und potentieller Energie, also L = T - V. Nicht?
| Zitat: | | Lass' mal zeitabhängige Probleme weg; das machts unübersichtlich und ist nicht unbedingt zielführend; letztlich kann jedes offene System auch als Teil eines abgeschlossenes Systems betrachtet werden |
Du weichst mir aus. Ja, ich mag auch lieber mit zeitunabhängigen Systemen rechnen. Mache ich auch fast nur. Dennoch habe ich mich gewundert, dass die Energie auf Lösungen in zeitabhängigen Systemen offenbar nicht konstant bleibt, obwohl man das System konservativ nennt. Ich dachte, die Definition von "konservativ" wäre gerade, dass die Energie konserviert wird und dass F = -dV/dx genau dies impliziert. Diese Vorstellung ist offenbar falsch. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18074
|
| TomS Verfasst am: 13. Jul 2021 19:49 Titel: |
|
|
| WebFritzi hat Folgendes geschrieben: | | Zitat: | | Die genaue Form von L = T - V folgt dann aus der bekannten Form für E sowie der Forderung, dass die Newtonschen sowie die Euler-Lagrangeschen Bewegungsgleichungen übereinstimmen. |
Die ELG folgen ja aus dem Prinzip der stat. Wirkung (PSW). Ok, und andersherum ... Daher erkenne ich so nicht an, dass die Form von L aus der bekannten Form für E sowie der Forderung, dass die Newtonschen sowie die Euler-Lagrangeschen Bewegungsgleichungen übereinstimmen folgt. Was ich suche, ist eine physikalische Motivation/Erklärung dafür, dass die Wirkung für die physikalischen Bahnen stationär ist und warum man L so wählt, wie man es wählt (L = T - V). |
L = T - V ist keine allgemeingültiger Ansatz; dies ist lediglich anwendbar für spezielle Systeme.
Wir müssen zwei Dinge auseinanderhalten:
A) Das Hamiltonsche Prinzip der stationären Wirkung ist soweit wir das heute verstehen allgemein anwendbar für beliebige Systeme und insbs. alle bekannten Theorien - Newtonsche Mechanik, Elektrodynamik ... ART ... Quantenmechanik, QED, QCD u.a. Quantenfeldtheorien; es besagt, dass die Dynamik eines Systems, das durch ein Wirkungsfunktional S beschrieben wird, aus der Forderung
folgt, wobei in der Variation verallgemeinerte Orte und Geschwindigkeiten als unabhängige Variablen betrachtet werden.
B) Darin ist noch keine Aussage bzgl. der genauen Form von S enthalten. Dies ist je System neu zu finden, und dabei gibt es keine allgemeingültigen Prinzipien - zumindest keine bekannten. Es funktioniert für die o.g. Theorien - Newtonsche Mechanik, Elektrodynamik ... - jeweils unterschiedlich *)
| WebFritzi hat Folgendes geschrieben: | | Beispiel: Ein Ball ... Eine solche Erklärung/Begründung hätte ich gerne für die Extremalität der Wirkung auf physikalischen Bahnen. |
Wie gesagt, dazu gibt es zwei Antworten: erstens das Hamiltonsche Prinzip der stationären Wirkung an sich, und zweitens eine spezielle Form von S für das jeweils betrachtete System.
| WebFritzi hat Folgendes geschrieben: | | Zitat: | | Lass dich aber nicht von dieser Form von L irritieren, das ist lediglich ein Spezialfall. |
??? Ich dachte, L ist immer die Differenz aus kinetischer und potentieller Energie, also L = T - V. Nicht? |
Nur in einfachen Fällen.
In der Newtonschen Mechanik folgt die Bewegungsgleichung eines einzelnen geladenen Teilchens in einem externen elektromagnetischen Feld aus der Wirkung
 - \dot{r}\,A(r)\right)\right])
In der speziellen Relativitätstheorie erhält man für den ersten Term stattdessen
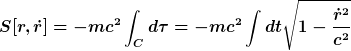
Aus dem zweiten Term kann insbs. die Lorentzkraft abgeleitet werden.
Der erste Term für die SRT, der im wesentlichen die Eigenzeit tau entlang einer Weltlinie C beschreibt, folgt aus Symmetrieüberlegungen. Er besagt, dass sich kräftefreie Teilchen entlang von Weltlinien extremaler Eigenzeit bewegen. Interessanterweise kann dies recht einfach für die ART verallgemeinert werden.
Außerdem reproduziert er natürlich die bekannte Form der kinetischen Energie der Netwonschen Theorie im Grenzfall
Der erste Term liefert eine andere funktionale Form der kinetischen Energie, der zweite Term ist kein Potential.
*) es gibt ein weiteres Prinzip, das speziell auf Quantenfeldtheorien zutrifft, aber das ist sehr spezifisch, technisch, nicht wirklich physikalisch, daher möchte ich das hier besser ausklammern
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
WebFritzi
Anmeldungsdatum: 07.02.2008
Beiträge: 13
|
| WebFritzi Verfasst am: 14. Jul 2021 02:51 Titel: |
|
|
Ich würde gerne bei klassischer Mechanik bleiben.
| Zitat: | | Darin ist noch keine Aussage bzgl. der genauen Form von S enthalten. Dies ist je System neu zu finden, und dabei gibt es keine allgemeingültigen Prinzipien - zumindest keine bekannten. |
Ok, und wie stellt man dann L bzw. S jeweils auf? Darum geht es mir ja. Woher weiß ich, dass eine von mir aufgestellte Funktion L die richtige für das gerade betrachtete System ist?
Ich kenne nur ein Skript, und da steht Folgendes drin:
Ein mechanisches System besteht aus N Masseteilchen und M Constraints (z.B. Kreisbahn eines Pendels). Die Constraints definieren die verallgemeinerten Koordinaten (VK). Nun müssen die Geschwindigkeiten der Teilchen noch in VK ausgedrückt werden. Damit bekommt man dann die kinetische Energie T (in VK). Zusätzlich gibt es jetzt Kräfte, die jeweils auf die Teilchen wirken. Auch die übersetzt man in VK und nimmt an, dass die Gesamtkraft ein Potential V besitzt (konservatives System). So, und jetzt ist L = T - V die Lagrangefunktion (LF). Fertig. Jetzt definiert man noch als S das Integral der LF und behauptet, dass physikalisch realistische Kurven stationäre Punkte von S sind.
Und ich frage: Wieso?
Bei diesem Setting würde ich gerne bleiben. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18074
|
| TomS Verfasst am: 14. Jul 2021 06:39 Titel: |
|
|
| WebFritzi hat Folgendes geschrieben: | Ich würde gerne bei klassischer Mechanik bleiben.
| Zitat: | | Darin ist noch keine Aussage bzgl. der genauen Form von S enthalten. Dies ist je System neu zu finden, und dabei gibt es keine allgemeingültigen Prinzipien - zumindest keine bekannten. |
Ok, und wie stellt man dann L bzw. S jeweils auf? |
Im Rahmen der klassischen Mechanik noch ohne Betrachtung von Constraints typischerweise
„Summe der kinetischen Energien minus Summe der Wechselwirkungsterme“
Letzteres sind, wie du am Beispiel der Wechselwirkung mit einen Magnetfeld erkennst, nicht unbedingt Potentiale.
Die Legendre-Transformation liefert dann die Hamiltonfunktion H, die mit der erhaltenen Energie E assoziiert ist.
| WebFritzi hat Folgendes geschrieben: | | Woher weiß ich, dass eine von mir aufgestellte Funktion L die richtige für das gerade betrachtete System ist? |
Physikalische Intuition plus Bestätigung im Zuge experimenteller Überprüfung.
| WebFritzi hat Folgendes geschrieben: | … Jetzt definiert man noch als S das Integral der LF und behauptet, dass physikalisch realistische Kurven stationäre Punkte von S sind.
Und ich frage: Wieso? |
Es gibt für derartige physikalische Prinzipien keine weitere Begründung. Ob du die Newtonschen Axiome begründen möchtest, die Relativitätstheorie, die spezielle Form eines Wechselwirkungsterms oder das Prinzip der kleinsten Wirkung – es läuft immer auf physikalische Intuition plus geeignete experimentelle Überprüfung hinaus.
Du bist Mathematiker. Auch in der Mathematik kannst du unterschiedliche Entitäten und Modelle einführen, für die du letztlich auf deine Intuition angewiesen bist.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18074
|
| TomS Verfasst am: 14. Jul 2021 08:46 Titel: |
|
|
Mir fällt ein, dass man aus der Quantenmechanik eine Begründung für das Prinzip der kleinsten Wirkung ableiten kann.
Aus der klassischen Hamiltonfunktion folgt der sogenannte Hamiltonoperator H. Die Wellenfunktion psi jedes beliebigen physikalischen Systems gehorcht der Schrödingergleichung. Damit gilt die Zeitentwicklung
 = e^{-iHt} \, \psi(0))
Diese Gleichung ist tatsächlich universell gültig.
Nun hat Feynman gezeigt, dass dies äquivalent ist zur Berechnung von Übergangswahrscheinlichkeiten ist, also zur Fragestellung „wie groß ist die Wahrscheinlichkeit, zum Zeitpunkt t' ein Teilchen bei x' zu finden, unter der Bedingung, dass es sich zum Zeitpunkt t bei x befunden hat?“
Feynman leitet dafür ein Objekt, das sogenannte Pfadintegral
ab, wobei S für die klassische Wirkung mit den o.g. Endpunkten x,t und x',t' steht.
Formal wird dabei über alle möglichen Pfade zwischen diesen Endpunkten integriert, daher das Symbol Dx.
Man kann zeigen, dass der dominierende Beitrag zu Z aus S_0 vom klassischen Pfad x_0 mit stationärer Wirkung stammt, d.h.
Der Term erster Ordnung verschwindet, da x_0 gerade die Euler-Lagrange-Gleichung erfüllt, so dass S_2 nur Terme mindestens zweiter Ordnung in der Abweichung x-Tilde enthält.
Aus der zuerst genannten Gleichung zur Zeitenwicklung eines beliebigen quantenmechanischen Systems folgt demnach, dass der dominierende Beitrag gerade von dem Pfad stammt, der ein Extremum der klassischen Wirkung darstellt.
Damit erscheint das Prinzip der stationären Wirkung als klassischer Grenzfall eines allgemeineren quantenmechanischen Prinzips.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
|
|
Registrieren
Login
FAQ
Suchen
