| Autor |
Nachricht |
annafragt
Anmeldungsdatum: 28.01.2021
Beiträge: 309
|
 annafragt Verfasst am: 26. Apr 2021 16:11 Titel: Vektoren Kreisscheibe annafragt Verfasst am: 26. Apr 2021 16:11 Titel: Vektoren Kreisscheibe |
 |
|
Meine Frage:
Hallo, ich bin leider sehr verwirrt und wollte daher mein Problem kurz darstellen:
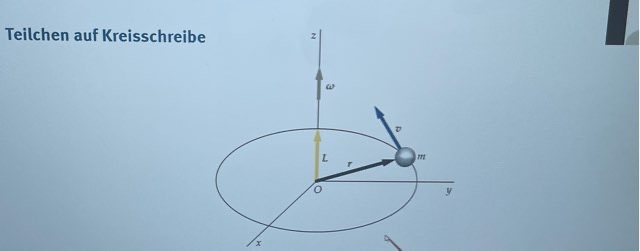
Es geht um folgende Abbildung, wo mein Prof meinte die Winkelgeschwindigkeit Omega steht senkrecht zu der Kreisscheibe, ja das kann ich sehen, und mithilfe der rechten Handregel ist dann der Daumen die winkelgeschwindigkeit und die restliche Hand zeigt die Bewegung des Massenpunktes.
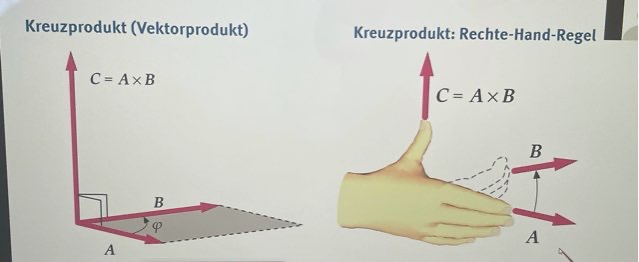
Das kann ich gar nicht nachvollziehen, denn ich dachte, dass w senkrecht auf v steht und r senkrecht auf v steht und dann v das Kreuzprodukt ist laut Definition, aber das kann ich hier in der Abbildung nicht mal so erkennen und auch wurde nicht erklärt, wie ich hier genau die rechte Hand anwenden soll.
Spielt es dann eine Rolle was für den Mittelfinger und was für den Zeigefinger steht?
Am wichtigsten wäre mir aber meine Verwirrung zu klären, wo ich sehe dass r senkrecht zu v und w zu v senkrecht ist.
Und eben wieso w ein Kreuzprodukt ist und von was dann?
Eine Antwort wäre toll, vielen dank
Meine Ideen:
Einen schönen Tag wünsche ich
| Beschreibung: |
|
| Dateigröße: |
18.76 KB |
| Angeschaut: |
2558 mal |
|
| Beschreibung: |
|
| Dateigröße: |
29.19 KB |
| Angeschaut: |
2558 mal |
|
|
|
 |
A.T.
Anmeldungsdatum: 06.02.2010
Beiträge: 343
|
|
 |
annafragt
Anmeldungsdatum: 28.01.2021
Beiträge: 309
|
 annafragt Verfasst am: 27. Apr 2021 07:40 Titel: annafragt Verfasst am: 27. Apr 2021 07:40 Titel: |
 |
|
Danke für die Antwort, folgendes wurde aber in der Vorlesung zusätzlich gesagt und angeblich an folgenden Bildern zu verdeutlichen sein. Ich verstehe aber leider gar nicht, was der Sinn dahinter sein soll bzw ich verstehe es nicht, weil es mich total mit dem dadrüber verwirrt oder vielleicht muss ich es nochmal anders erklärt und evtl ziemlich herunter gebrochen erklärt bekommen:
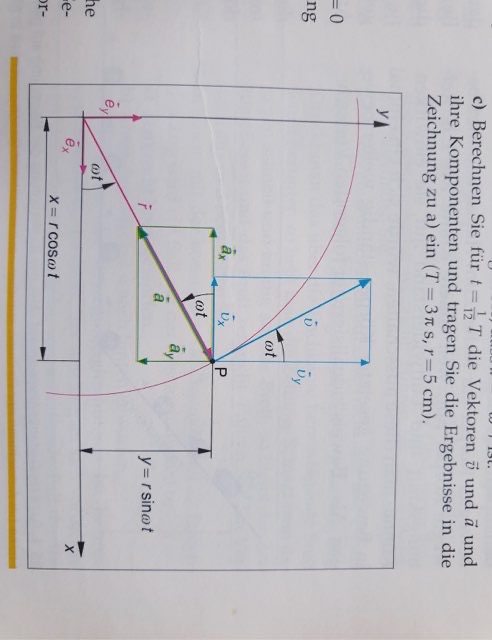
Die rechte Hand Regel soll eine Hilfestellung sein, in welche Richtung der Vektor der Winkelgeschwindigkeit zeigt. Bei der Rotation gegen den Uhrzeigersinn aus der Papierebene heraus, bei der Rotation im Uhrzeigersinn in die Tafelebene hinein. Die Fingerspitzen zeigen in die Bewegungsrichtung. Auch dies kann man mit einem Kreuzprodukt erklären, da ein Punkt S in der Zeit delta t um den Winkel delta alpha zum Punkt S' auf der Kreisbahn bewegt wird und so das Kreissegment, die Bahngeschwindigkeiten zum Punkt S und S' und die Zentripetalbeschleunigung ar gegeben sind.
Aufgrund von Ähnlichkeitsüberlegung (gleicher Winkel zwischen den Ortsvektoren r und r' und den Geschwindigkeiten v und v') können wir zunächst die Richtungen und Beträge aber nicht die Angriffspunkte der Vektoren für Geschwindigkeit v, Winkelgeschwindigkeit w und Ortsvektor r und Zentripetalbeschleunigung a_r betrachten, wobei ar_r antiparallel zu r ist!
Ich würde mich über Erläuterung sehr freuen da ich sehr verwirrt bin. Ich verstehe auch nicht, wofür das wichtig wär.
Vielen Dank schonmal
| Beschreibung: |
|
| Dateigröße: |
58.04 KB |
| Angeschaut: |
2467 mal |
|
| Beschreibung: |
|
| Dateigröße: |
66.67 KB |
| Angeschaut: |
2470 mal |

|
|
|
 |
A.T.
Anmeldungsdatum: 06.02.2010
Beiträge: 343
|
 A.T. Verfasst am: 27. Apr 2021 08:08 Titel: A.T. Verfasst am: 27. Apr 2021 08:08 Titel: |
 |
|
| annafragt hat Folgendes geschrieben: | | ....vielleicht muss ich es nochmal anders erklärt und evtl ziemlich herunter gebrochen erklärt bekommen |
Das wird an vielen Stellen im Internet erklärt, auch mit anschlichen Animationen. Hast du mal gesucht?
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 27. Apr 2021 08:26 Titel: Myon Verfasst am: 27. Apr 2021 08:26 Titel: |
 |
|
Ich weiss nicht, ob das etwas weiterhilft:
Man merkt sich wahrscheinlich am einfachsten
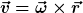
Aber auch 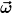 und und 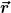 können jeweils als Vektorprodukt der anderen Vektoren ausgedrückt werden. können jeweils als Vektorprodukt der anderen Vektoren ausgedrückt werden.  bilden ein Rechtssystem und können, was die Richtung angeht, jeweils zyklisch vertauscht werden. bilden ein Rechtssystem und können, was die Richtung angeht, jeweils zyklisch vertauscht werden.
Multipliziert man die obige Gleichung von links vektoriell mit 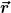 , erhält man , erhält man
=\vec{\omega}(\vec{r}\cdot\vec{r})-\vec{r}(\vec{r}\cdot\vec{\omega})=\vec{\omega}r^2)

Dabei wurde diese Identität benutzt. Es kann also auch für 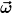 die „Rechte-Hand-Regel“ (oder was immer einem am einfachsten dünkt) verwendet werden, wie oben angegeben. die „Rechte-Hand-Regel“ (oder was immer einem am einfachsten dünkt) verwendet werden, wie oben angegeben.
Analog erhält man

|
|
 |
annafragt
Anmeldungsdatum: 28.01.2021
Beiträge: 309
|
 annafragt Verfasst am: 27. Apr 2021 09:08 Titel: annafragt Verfasst am: 27. Apr 2021 09:08 Titel: |
 |
|
| A.T. hat Folgendes geschrieben: | | annafragt hat Folgendes geschrieben: | | ....vielleicht muss ich es nochmal anders erklärt und evtl ziemlich herunter gebrochen erklärt bekommen |
Das wird an vielen Stellen im Internet erklärt, auch mit anschlichen Animationen. Hast du mal gesucht? |
Danke für die Antwort. Ich habe da irgendwie leider nichts zu gefunden. Kennst du eine Seite mit einer Animation zu dieser Thematik?
Danke nochmal
|
|
 |
annafragt
Anmeldungsdatum: 28.01.2021
Beiträge: 309
|
 annafragt Verfasst am: 27. Apr 2021 09:12 Titel: annafragt Verfasst am: 27. Apr 2021 09:12 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | Ich weiss nicht, ob das etwas weiterhilft:
Man merkt sich wahrscheinlich am einfachsten
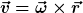
Aber auch 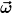 und und 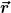 können jeweils als Vektorprodukt der anderen Vektoren ausgedrückt werden. können jeweils als Vektorprodukt der anderen Vektoren ausgedrückt werden.  bilden ein Rechtssystem und können, was die Richtung angeht, jeweils zyklisch vertauscht werden. bilden ein Rechtssystem und können, was die Richtung angeht, jeweils zyklisch vertauscht werden.
Multipliziert man die obige Gleichung von links vektoriell mit 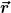 , erhält man , erhält man
=\vec{\omega}(\vec{r}\cdot\vec{r})-\vec{r}(\vec{r}\cdot\vec{\omega})=\vec{\omega}r^2)

Dabei wurde diese Identität benutzt. Es kann also auch für 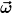 die „Rechte-Hand-Regel“ (oder was immer einem am einfachsten dünkt) verwendet werden, wie oben angegeben. die „Rechte-Hand-Regel“ (oder was immer einem am einfachsten dünkt) verwendet werden, wie oben angegeben.
Analog erhält man
 |
Vielen Dank für die Antwort, doch es hilft.
Ich habe jedoch noch zwei Unklarheiten:
1. das kann ich mir irgendwie nicht vorstellen: Die rechte Hand Regel soll eine Hilfestellung sein, in welche Richtung der Vektor der Winkelgeschwindigkeit zeigt. Bei der Rotation gegen den Uhrzeigersinn aus der Papierebene heraus, bei der Rotation im Uhrzeigersinn in die Tafelebene hinein. Die Fingerspitzen zeigen in die Bewegungsrichtung.
Wo zeigt dann genau welcher Finger (und somit jeder Vektor jeweils hin zB Omega nach oben etc) oder gibt es eine Animation oder sonst irgendwas?
2.
Ich verstehe den Sinn folgender Passage nicht: „Aufgrund von Ähnlichkeitsüberlegung (gleicher Winkel zwischen den Ortsvektoren r und r' und den Geschwindigkeiten v und v') können wir zunächst die Richtungen und Beträge aber nicht die Angriffspunkte der Vektoren für Geschwindigkeit v, Winkelgeschwindigkeit w und Ortsvektor r und Zentripetalbeschleunigung a_r betrachten, wobei ar_r antiparallel zu r ist“
Was bedeutet dass r zu ar_r antiparallel ist?
Danke nochmal
|
|
 |
A.T.
Anmeldungsdatum: 06.02.2010
Beiträge: 343
|
 A.T. Verfasst am: 27. Apr 2021 09:28 Titel: A.T. Verfasst am: 27. Apr 2021 09:28 Titel: |
 |
|
| annafragt hat Folgendes geschrieben: |
Wo zeigt dann genau welcher Finger (und somit jeder Vektor jeweils hin zB Omega nach oben etc) oder gibt es eine Animation oder sonst irgendwas?
|
Siehe links in meinen Post oben.
| annafragt hat Folgendes geschrieben: |
Was bedeutet dass r zu ar_r antiparallel ist?
|
Genau entgegengesetzt.
|
|
 |
annafragt
Anmeldungsdatum: 28.01.2021
Beiträge: 309
|
 annafragt Verfasst am: 27. Apr 2021 12:14 Titel: annafragt Verfasst am: 27. Apr 2021 12:14 Titel: |
 |
|
| A.T. hat Folgendes geschrieben: | | annafragt hat Folgendes geschrieben: |
Wo zeigt dann genau welcher Finger (und somit jeder Vektor jeweils hin zB Omega nach oben etc) oder gibt es eine Animation oder sonst irgendwas?
|
Siehe links in meinen Post oben.
| annafragt hat Folgendes geschrieben: |
Was bedeutet dass r zu ar_r antiparallel ist?
|
Genau entgegengesetzt. |
Okay danke. Und wie kommt man jetzt von den ganzen Überlegungen über Omega auf einmal auf a und packt es damit rein? Das war doch in meinem Kreuzprodukt gar nicht dabei oder?
Kreuzprodukt von w war wie es Myon angegeben hat und Kreuzprodukt von a ist w x v, aber was jetzt der Sinn ist..
Irgendwie löst sich meine Verwirrung nicht. Kann man da noch Licht ins Dunkel bringen? Vielen dank
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 27. Apr 2021 12:56 Titel: Nils Hoppenstedt Verfasst am: 27. Apr 2021 12:56 Titel: |
 |
|
| annafragt hat Folgendes geschrieben: |
Kreuzprodukt von w war wie es Myon angegeben hat und Kreuzprodukt von a ist w x v, aber was jetzt der Sinn ist..
|
Der Sinn dahinter ist, dass v, r, w und a zueinander in einer festen Beziehung stehen. Kennt man zwei der Größen, kann man über die angegebenen Formeln die jeweils anderen beiden Größen ausrechnen.
- Nils
|
|
 |
A.T.
Anmeldungsdatum: 06.02.2010
Beiträge: 343
|
|
 |
Qubit
Anmeldungsdatum: 17.10.2019
Beiträge: 851
|
 Qubit Verfasst am: 27. Apr 2021 16:55 Titel: Qubit Verfasst am: 27. Apr 2021 16:55 Titel: |
 |
|
| annafragt hat Folgendes geschrieben: |
Am wichtigsten wäre mir aber meine Verwirrung zu klären, wo ich sehe dass r senkrecht zu v und w zu v senkrecht ist.
Und eben wieso w ein Kreuzprodukt ist und von was dann?
Eine Antwort wäre toll, vielen dank
|
Du solltest dich intensiver mit dem "Vektorkalkül" (Vektorrechnung) beschäftigen, dann sollte es dir auch klarer werden. Dazu ist immer hilfreich, sich Sachverhalte an einfachsten Beispielen klar zu machen.
Mal zur Motivation:
Winkelgeschwindigkeiten treten da auf, wo du Drehbewegungen beschreiben willst. Um Drehbewegungen zu beschreiben, brauchst du eine Drehachse und einen Drehwinkel. In 3 Dimensionen lässt sich dazu ein "Drehvektor" verwenden.
Betrachte als einfaches Beispiel die Drehung um die z-Achse als Drehachse (Richtung) mit einer ebenen Drehung um einen Winkel  , der Ortsvektor (fixer Abstand R) wird dann gedreht: , der Ortsvektor (fixer Abstand R) wird dann gedreht:
 \\ sin (\varphi) \end{pmatrix})
Hast du eine gleichförmige Drehbewegung, ist der Winkel linear in der Zeit:
 = \omega \cdot t)
Also:
 \\ sin (\omega \cdot t) \end{pmatrix})
Der Geschwindigkeitvektor ist die zeitliche Ableitung:
 \\ cos (\omega \cdot t) \end{pmatrix})
mit
 + cos^2(\omega \cdot t)} = \omega R)
Man sieht auch, dass v und r orthogonal sind:
 \cdot cos(\omega R) + cos(\omega R) \cdot sin(\omega R))= 0)
Ist nun der Ortsvektor nicht in der x-y-Ebene, sondern hat eine z-Komponente (bildet mit der Drehachse einen Winkel), dann ist das Skalarprodukt ebenfalls null, wie man schnell sieht, da die z-Komponente von v ebenfalls Null ist:
 \\ sin (\omega \cdot t) \\ z\end{pmatrix})
 \\ cos (\omega \cdot t) \\ 0\end{pmatrix})

Offenbar hängt der Geschwindigkeitsvektor nur vom orthogonalen Abstand zur Drehachse ab, also vom Sinus des Winkels zwischen Drehachse und Ortsvektor. (mal dir am Besten dazu ein Bild).
Der Betrag des Geschwindigkeitsvektors muss also allgemeiner sein:
)
 : Winkel zwischen Drehachse und Ortsvektor : Winkel zwischen Drehachse und Ortsvektor
Der Beschleunigungvektor ist die zeitliche Ableitung des Geschwindigkeitsvektors:
 \\ sin (\omega \cdot t) \\ 0 \end{pmatrix})
Der Beschleunigungsvektor ist also antiparallel zur Projektion des Ortsvektors in die x-y-Ebene (für z=0 ist er direkt antiparallel).
Wie sieht nun die Drehung als Drehvektor (in 3 Dimensionen) aus?
Offenbar ist nach der letzten Beziehung für den Geschwindigkeitsvektor der Geschwindigkeitvektor so etwas wie ein "Vektorprodukt" aus dem Drehvektor und Ortsvektor.
 \\ sin (\omega \cdot t) \\ z\end{pmatrix} \stackrel{!}{=}
<br />
\omega \cdot R \cdot sin(\alpha) \begin{pmatrix}-sin (\omega \cdot t) \\ cos (\omega \cdot t) \\ 0\end{pmatrix})
Also:

Da v orthogonal zu r ist, lässt sich dies auch als lineare Abbildung (Matrix) schreiben:
 \begin{pmatrix} x \\ y \\ z \end{pmatrix})
Diese Abbildung als Darstellung von omega lässt sich nun verallgemeinern, wenn die Drehachse nicht nur in z-Richtung sondern in einer beliebigen Richtung liegt. Hierfür braucht man etwas lineare Algebra (dazu kannst du etwas recherchieren). Als allgemeine Beziehung bekommst du dann für v:
 \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} -\omega_z \cdot y + \omega_y \cdot z \\ \omega_z \cdot x - \omega_x \cdot z \\ -\omega_y \cdot x + \omega_x \cdot y \end{pmatrix})
omega ist also auch eine antisymmetrische Matrix (genauer: antisymmetrischer Tensor) und das Produkt der Vektoren ist das sogenannte Vektorprodukt:

Dass der Betrag von v gerade die angegebene Parallelogrammfläche der Vektoren von omega und r ist, kann man sich auch geometrisch herleiten:
 = |\vec \omega||\vec r| \cdot \sqrt{1-cos^2(\alpha)} = \sqrt{(|\vec \omega||\vec r|)^2-(|\vec \omega||\vec r|)^2 cos^2(\alpha)})
(\vec r \cdot \vec r)-(\vec \omega \cdot \vec r)^2} = \sqrt{(\omega^2_x + \omega^2_y + \omega^2_z)(x^2 + y^2 + z^2)-(\omega_x \cdot x + \omega_y \cdot y + \omega_z \cdot z)^2})
Den Radikanden kann man nun ausmultiplizieren und umsortieren (das überlasse ich dir), man erhält dann:
^2 +(\omega_z \cdot x - \omega_x \cdot z)^2 +(\omega_x \cdot y - \omega_y \cdot x)^2})
Man sieht auch, dass Geschwindigkeitvektor und Winkelgeschwindigkeitsvektor orthogonal sind:



Jetzt beachte man noch, dass die Winkelgeschwindigkeit ein "axialer Vektor" ist, also invariant unter Punktspiegelungen ist. r und v sind dagegen "polare Vektoren":


PS: du kannst dir ja jetzt mal überlegen, wie die Beziehungen ausschauen, wenn omega und r keine konstanten Beträge haben.
|
|
 |
Tina S.
Gast
|
 Tina S. Verfasst am: 28. Apr 2021 09:44 Titel: Tina S. Verfasst am: 28. Apr 2021 09:44 Titel: |
 |
|
Dazu ist immer hilfreich, sich Sachverhalte an einfachsten Beispielen klar zu machen.

|
|
 |
|




















