| Autor |
Nachricht |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18108
|
 TomS Verfasst am: 04. Feb 2021 23:21 Titel: FAQ - Lichtgeschwindigkeit, universelle Grenzgeschwindigkeit TomS Verfasst am: 04. Feb 2021 23:21 Titel: FAQ - Lichtgeschwindigkeit, universelle Grenzgeschwindigkeit |
 |
|
Ich fasse hier mal die etwas längere Überlegung zur folgenden Frage zusammen: wie kann man mittels der Relativitätstheorie begründen, warum sich nichts schneller als das Licht bewegen kann, warum die Lichtgeschwindigkeit also eine universelle Grenzgeschwindigkeit darstellt?
[Da dies aus einem Thread entstanden ist, muss ich dies evtl. noch etwas straffen]
Teil 1
Prinzipiell vollumfänglich begründen kann man dies überhaupt nicht, da es durchaus mathematische Modelle gibt, die in sich konsistent sind und die beliebige Grenzgeschwindigkeiten einschließlich Unendlich zulassen. Man benötigt also weitere theoretische Annahmen (Axiome, Physiker sprechen eher von Postulaten) sowie daraus abgeleitete, experimentell überprüfbare Vorhersagen, die dann auch tatsächlich durch Beobachtungen bestätigt werden.
Die Frage warum sich nichts schneller als das Licht bewegen kann, läuft dann unweigerlich auf die Frage hinaus, warum gerade diese Postulate vorausgesetzt werden - und keine anderen. Das kann man weitertreiben, es gibt keine letzt- oder endgültige Antwort.
Man kann sich jedoch auf vernünftige, einfache und zugleich mächtige Postulate einigen, so dass aus möglichst wenig elementaren Annahmen möglichst viele, experimentell zutreffende Vorhersagen abgeleitet werden können. Die Postulate, von denen Einstein bei der Entwicklung der Speziellen Relativitätstheorie ausging, sind diesbzgl. ein gutes Beispiel:
Das Relativitätsprinzip: Die Gesetze der Physik nehmen in allen Inertialsystemen die gleiche Form an.
Die Konstanz der Lichtgeschwindigkeit: Die Lichtgeschwindigkeit im Vakuum ist in allen Inertialsystemen gleich.
(Inertialsystem ist ein sehr technischer Begriff und erfordert eine Erklärung; sinngemäß könnte man auch fordern, dass die Gesetze der Physik durch Gleichungen beschrieben werden, die jeder Beobachter in seinem Bezugsystem formulieren kann, und die dabei in allen diesen Bezugsystemen = für alle Beobachter die selbe Form annehmen; Form muss man ebenfalls noch erklären)
Aus dem Relativitätsprinzip folgt, dass jede Geschwindigkeit eines Objekts immer nur eine Relativgeschwindigkeit ist, d.h. sie muss bezüglich eines Bezugs- oder Inertialsystem angegeben werden. Letztlich folgt daraus, dass man Geschwindigkeiten ineinander umrechnen kann und muss, wenn man das Bezugsystem wechselt (dies ist bereits bei Newton der Fall; man spricht vom Relativitätsprinzip nach Galilei).
Das Prinzip von der Konstanz der Lichtgeschwindigkeit bedeutet insbs., dass diese unabhängig von der Geschwindigkeit der Lichtquelle oder des Beobachters ist. Das steht im Widerspruch zum Relativitätsprinzip nach Galilei, demzufolge jede Umrechnung einer Geschwindigkeit zu einem anderen Wert führt (es sei denn, die Lichtgeschwindigkeit wäre unendlich; man kann jedoch experimentell überprüfen, dass dies nicht zutrifft). Wenn ein Beobachter B einem Objekt O die Geschwindigkeit v zuschreibt, so wird ein zweiter Beobachter B‘, der sich bzgl. B mit einer Relativgeschwindigkeit u bewegt, dem Objekt die Geschwindigkeit v‘ = v - u zuschreiben (Spezialfall v=u, B‘ bewegt sich gleich schnell wie O, d.h. v‘ = 0).
Daraus folgt, dass die bekannte Methode der Addition von Geschwindigkeiten modifiziert werden muss, da andernfalls auch c‘ = c - u gelten müsste - im Widerspruch zum Prinzip der Konstanz der Lichtgeschwindigkeit. Rein logisch erfordert dieses Prinzip also einen neuen kinematischen Rahmen, der sich natürlich teilweise auf den Newtonschen Rahmen reduzieren muss, aus dem ja im Alltag zutreffende Vorhersagen folgen.
Das Prinzip von der Konstanz der Lichtgeschwindigkeit hat nun zwei Schächen:
i) es sieht so aus, als gälte es nur speziell für Licht
ii) es erklärt die Konstanz der Lichtgeschwindigkeit nicht, es postuliert sie lediglich.
Ersteres lässt sich historisch dadurch erklären, dass Einstein insbs. die Maxwellsche Theorie der Elektrodynamik bekannt war, die speziell für Licht gilt und aus der die Lichtgeschwindigkeit als Konstante im Sinne dieses Prinzips folgt. Die Maxwellsche Theorie stellt also in gewisser Weise eine spezielle Erklärung für Licht dar.
Ziel solle es jedoch sein, ein anderes, fundamentales Prinzip zu finden, aus dem zusammen mit dem Relativitätsprinzip die Konstanz der Lichtgeschwindigkeit abgeleitet werden kann, besser gesagt, aus dem eine universelle Grenzeschwindigkeit für beliebige Phänomene folgt, wobei die Lichtgeschwindigkeit lediglich einen Spezialfall darstellt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 05. Feb 2021 07:40, insgesamt 2-mal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18108
|
 TomS Verfasst am: 04. Feb 2021 23:22 Titel: TomS Verfasst am: 04. Feb 2021 23:22 Titel: |
 |
|
Einschub
Es gibt diverse Ansätze, auf das zweite Postulat zu verzichten und stattdessen Homogenität und Isotropie zu fordern.
https://zenodo.org/record/1424203
http://synset.com/pdf/100_en.pdf
https://arxiv.org/pdf/physics/0302045v1.pdf
https://arxiv.org/pdf/1412.4018.pdf
Im wesentlichen stimmen die Ansätze darin überein, dass nur drei mögliche linear-affine Transformationen mit dem Relativitätsprinzip sowie Homogenität und Isotropie vereinbar sind
Galilei-Invarianz (entspr. c = ∞)
Lorentz- bzw. Poincare-Invarianz (c)
(c = 0)
Da die Galilei-Invarianz experimentell widerlegt ist (c < ∞), bleibt die Lorentz- bzw. Poincare-Invarianz, die jedoch die Galilei-Invarianz als Grenzfall sehr kleiner Geschwindigkeiten enthält.
Außerdem können mittels Relativitätsprinzip sowie detailliert gruppentheoretisch *) drei „unverbundene“ Klassen von Teilchen identifiziert werden
v < c (m > 0, zeitartige)
v = c (m = 0, lichtartige)
v > c (m² < 0, tachonisch)
Letztere dürfen nicht zu v < c wechseln bzw. mit gewöhnlichen Teilchen in Wechselwirkung treten, da dies eine Verletzung der Kausalität zur Folge hätte *)
*) folgt erst mittels Lorentz- bzw. Poincare-Transformation, die noch abzuleiten ist.
M.E. müssen jedenfalls sämtliche Argumente für die drei Klassen separat untersucht werden.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 05. Feb 2021 07:42, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18108
|
 TomS Verfasst am: 04. Feb 2021 23:23 Titel: TomS Verfasst am: 04. Feb 2021 23:23 Titel: |
 |
|
Teil 2
Zusammenfassend kommen die oben zitierten Arbeiten zu dem Schluss, dass das zweite Postulat in
Das Relativitätsprinzip: Die Gesetze der Physik nehmen in allen Inertialsystemen die gleiche Form an.
Die Konstanz der Lichtgeschwindigkeit: Die Lichtgeschwindigkeit im Vakuum ist in allen Inertialsystemen gleich.
nicht fundamental ist sondern durch Homogenität und Isotropie ersetzt werden kann. Wir gelangen also zu
Das Relativitätsprinzip: Die Gesetze der Physik nehmen in allen Inertialsystemen die gleiche Form an.
Die Homogenität und Isotropie der Raumzeit: Die Geometrie der Raumzeit zeichnet keine Orte oder Richtungen aus.
Aus diesen beiden Postulaten folgt, dass jede physikalische Theorie auf einer derartigen 4-dim. Raumzeit entsprechende Symmetrien aufweisen sollte, d.h. dass die Theorie mittels eines Wirkungsprinzips formuliert wird, wobei die Wirkung invariant unter der 10-dim. Symmetriegruppe dieser homogenen und isotropen Raumzeit ist. Desweiteren kann motiviert werden, dass diese Symmetrien mittels einer linearen Darstellung einer Liegruppe zu implementieren sind (ich sehe nicht, dass diese Argumente mathematisch zwingend sind und dass es keine anders gearteten Symmetriestrukturen geben kann)
Die Arbeiten argumentieren außerdem, dass aus der 4-dim. Darstellung dieser linearen Symmetriegruppe auf den Vierervektoren zwingend folgt, dass diese Symmetriegruppe einen einzigen freien Parameter c mit Dimension einer Geschwindigkeit enthält, und dass die Symmetrie für c = ∞ der Galilei- bzw. für c < ∞ der Poincare-Invarianz entspricht.
Zwischen diesen beiden Möglichkeiten kann experimentell unterschieden werden, der Wert von c wird als Naturkonstante mittels Messungen festgelegt.
In der Hamiltonschen Formulierung mit
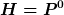
wirken die 10 Größen - 4 Translationen, 3 Rotationen, 3 Boosts -
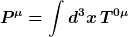
 = x^i \, P^k - x^k P^i)
 = x^0 \, P^i - x^i P^0 \sim \gamma m (vt - x))
als Generatoren der entsprechenden Transformationen der 10-dim. Poincare-Gruppe.
Nach dem Noether-Theorem folgen aus der Invarianz der Wirkung 7 Erhaltungsgrößen. Die Symmetrie bzw. die Ladungserhaltung wird dabei durch die Poisson-Klammern ausgedrückt
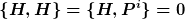
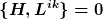
Man beachte, dass diese Argumentation für jede beliebige Theorie gilt, die mit den beiden o.g. Postulaten verträglich ist, d.h. dass zunächst die Symmetriestruktur der Raumzeit fundamental ist und jede entsprechende Theorie diese lediglich „erbt“; außerdem ist der Wert von c universell, d.h. für alle Theorien auf dieser Raumzeit identisch; insofern ist Licht eben nicht ausgezeichnet.
Kurz: Die Existenz einer universellen Geschwindigkeit c basiert auf der geometrischen Struktur der Raumzeit; diese folgt letztlich aus den Postulaten der Homogenität und Isotropie sowie aus dem Relativitätsprinzip.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18108
|
 TomS Verfasst am: 04. Feb 2021 23:24 Titel: TomS Verfasst am: 04. Feb 2021 23:24 Titel: |
 |
|
Teil 3
Zusammenfassung der bisherigen Ergebnisse:
Aus den beiden Postulaten
Das Relativitätsprinzip: Die Gesetze der Physik nehmen in allen Inertialsystemen die gleiche Form an.
Die Homogenität und Isotropie der Raumzeit: Die Geometrie der Raumzeit zeichnet keine Orte oder Richtungen aus.
sowie der Implementierung einer entsprechenden Symmetrie mittels einer linearen, reellen, 4-dim. Darstellung einer Liegruppe auf dem Vektorraum der Vierervektoren folgt eine 10-dim. Symmetriegruppe, die einen einzigen freien Parameter c mit Dimension einer Geschwindigkeit enthält; für die Symmetrie folgen genau zwei Möglichkeiten:
c = ∞ mit Galilei- bzw.
c < ∞ mit Poincare-Invarianz.
Ersteres kann ausgeschlossen werden; c wird experimentell bestimmt (beides mittels der Elektrodynamik)
Der Parameter c ist universell, d.h. er hat für alle Theorien, die auf dieser Raumzeit betrachtet werden (Punktteilchen, Elektrodynamik, Quantenfeldtheorien beliebiger Wechselwirkungen ...) den selben Wert (und muss speziell für die Elektrodynamik mit der Lichtgeschwindigkeit assoziiert werden).
Damit existiert eine universelle Geschwindigkeit c.
Dass diese als universelle Grenzgeschwindigkeit aufgefasst werden kann, ist nun nicht universell. Es existieren drei „unverbundene“ Klassen von Teilchen
v < c (m > 0, zeitartige)
v = c (m = 0, lichtartige)
v > c (m² < 0, tachonisch)
v > c erscheint bei weiteren Überlegungen pathologisch und wird ausgeschlossen, jedoch nur in Verbindung mit weiteren physikalischen Prinzipien; rein geometrisch ist dieser Fall zulässig.
v = c gilt strikt für m = 0, d.h. es folgt rein geometrisch, dass für masselose Teilchen v < c unzulässig ist.
v < c gilt strikt für m > 0, d.h. es folgt ebenfalls rein geometrisch, dass für masselose Teilchen v = c unzulässig ist; dies entspricht der Tatsache, dass v = c eine universelle obere Grenzgeschwindigkeit für massebehaftete Teilchen darstellt.
Viele weiteren „Erklärungen“ für diese Tatsache sind Schlussfolgerung aus diesen geometrischen Überlegungen.
(im folgenden setze ich c = 1)
Relativistische Geschwindigkeitsaddition für massebehaftete Teilchen: diese folgt für Geschwindigkeiten v im wesentlichen aus einem Lorentz-Boost mit Geschwindigkeit u angewandt auf die Vierergeschwindigkeit
)
d.h.
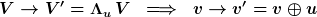
D.h. letztlich stellt die o.g. Poincare-Invarianz sicher, dass Geschwindigkeiten auf < c beschränkt bleiben.
Divergenz der kinetischen Energie für massebehaftete Teilchen: diese folgt im wesentlichen wieder aus einem Lorentz-Boost mit Geschwindigkeit u angewandt auf einen Viererimpuls im Ruhesystem des Teilchens, d.h.
)
mit
 = m \, \gamma_u \, (1,u) )
D.h. letztlich folgt die Divergenz der Energie aus der o.g. Poincare-Invarianz.
Wellengleichungen: Die Grundlegende Idee besteht in der Lösung eines Anfangswertproblems auf raumartigen Hyperflächen; Störungen breiten sich längs der sogenannten Charakteristiken aus. Für Differentialgleichungen wie z.B.
 = 0)
entsprechen die Charakteristiken gerade dem Lichtkegel in x_0
 = x_0 \pm ct )
d.h. Störungen propagieren auf (bzw. für m > 0 innerhalb) des Lichtkegels. Dies folgt letztlich Invarianz des Differentialoperators.
Quantenfeldtheorie: zunächst erzwingt die Poincare-Invarianz Wellengleichungen der Form
 \, \phi(x) = 0)
für ein Skalarfeld (bzw. analoge Gleichungen für Spin > 0)
Daraus folgen die Propagatoren G im Orts- bzw. Impulsraum
 \, G(x-y) = -\delta^{(4)}(x-y))
 \, G(p) = -1)
Die Forderung der Kausalität bzw. der Vorwärts-Propagation in der Zeit erzwingt, dass die retardierten Propagatoren im Ortsraum verschwinden, wenn x-y außerhalb des Lichtkegels liegt, d.h. wenn x und y raumartigen zueinander sind (für den Feynman-Propagator ist das etwas trickreicher).
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18108
|
 TomS Verfasst am: 04. Feb 2021 23:25 Titel: TomS Verfasst am: 04. Feb 2021 23:25 Titel: |
 |
|
Zum Abschluss
Ich fasse kurz zusammen, warum dieser etwas indirekte Zugang notwendig war und was die wesentliche Leistung der RT ist.
Zunächst wurde nach einer Begründung für Lichtgeschwindigkeit als Grenzgeschwindigkeit gefragt. Auf Basis der ursprünglichen Postulate Einsteins kann dies nicht wirklich begründet werden, da die Sonderrolle der Lichtgeschwindigkeit bereits in den Postulaten enthalten ist.
Gesucht ist also ein modifizierter axiomatischer Zugang, der zunächst vollständig ohne eine ausgezeichnete Geschwindigkeit formuliert werden kann, und der darüber hinaus allgemeingültig ist (statt auf das Phänomen „Licht“ verengt, was letztlich historische Gründe hat).
Die Forderung nach Homogenität und Isotropie des Raumes - zusammen mit dem unveränderten Relativitätsprinzip - leisten genau dies.
Ausgehend von diesen Postulaten folgt die SRT als Meta-Theorie; sie schafft einen universellen geometrischen Rahmen für alle weiteren Theorien, die auf dieser Raumzeit formuliert werden.
D.h. die Konstruktionsprinzipien
- die Existenz einer universellen Geschwindigkeit,
- die Poincare-Transformation als Symmetriestruktur der Raum-Zeit
- und aller darauf zu formulierenden Theorien sowie deren zulässige mathematische Strukturen
folgen aus
- zwei fundamentalen Postulaten
- dem experimentellen Nachweis einer endlichen Ausbreitungsgeschwindigkeit masseloser Teilchen.
Dies ist ein extrem starke Vorhersage: es kann keine zwei Feldtheorien geben, die voneinander abweichende Ausbreitungsgeschwindigkeit masseloser Teilchen aufweisen, und die mit der SRT sowie untereinander verträglich sind; anders formuliert: würden neue masselose Teilchen nachgewiesen werden, die eine andere Ausbreitungsgeschwindigkeit aufweisen, würde dies die SRT und alle darauf basierenden Theorien und bisher etablierten Theorien widerlegen. Kurz: der Nachweis eines masselosen, nicht elektromagnetisch wechselwirkenden Teilchens mit einer anderen Ausbreitungsgeschwindigkeit als der des Lichts falsifiziert die SRT sowie das gesamte Standardmodell.
Dies unterscheidet die RT fundamental von anderen physikalischen Theorien; deswegen nenne ich sie Meta-Theorie.
Dies bedeutet beispielsweise, dass die klassischen Phänomene "Licht u.a. el.-mag. Wellen" mit den Eigenschaften "zwei Polarisationen", "konstante Ausbreitungsgeschwindigkeit" und "Linearität" durch die Maxwellsche Theorie beschrieben werden müssen. Ähnliches gilt für weitere Feldtheorien, die wir heute im Standardmodell zusammenfassen oder als Erweiterungen desselben begreifen.
In gleicher Weise stellt die ART eine Meta-Theorie für die Konstruktion weiterer Feldtheorien zur Beschreibung gravitativ wechselwirkender Materie dar (das einzige seit Einstein fundamental neue geometrische Prinzip stellt wohl die lokale Supersymmetrie dar).
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18108
|
 TomS Verfasst am: 05. Feb 2021 07:57 Titel: TomS Verfasst am: 05. Feb 2021 07:57 Titel: |
 |
|
Anmerkungen zur Poincare-Invarianz
Aus der globalen Symmetrie unter den Transformation g einer Gruppe G auf der Raumzeit folgt nach dem Noether-Theorem ein erhaltener Strom j. Im Falle der Poincare-Transformationen sind die Lorentz-Transformationen (Rotationen und Boosts) sowie Translationen. Angewandt auf Vierervektoren
^\mu = \Lambda^\mu_\nu \, x^\nu + a^\mu)
Der erhaltene Strom lautet
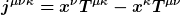
 = \delta_\mu^\nu T^{\mu\kappa} - \delta_\mu^\kappa T^{\mu\nu} = T^{\nu\kappa} - T^{\kappa\nu} = 0)
Dabei steht T für den Energie-Impuls-Tensor der jeweils betrachteten Theorie.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
|
|















