FAQ - Bindungsenergie und Massendefekt

TomS · Moderator Anmeldungsdatum: 20.03.2009 Beiträge: 18067

Hier eine Zusammenfassung einer Diskussion zum Thema Bindungsenergie und Massendefekt.

Im folgenden werden Prozesse diskutiert, bei denen zwei zunächst freie Teilchen ein gebundenes System bilden. Zwei Beispiele sind Einfang bzw. Fusion von i) Proton und Neutron oder ii) zwei Protonen durch die Starke Wechselwirkung / Kernkraft mit Entstehung eines Deuterons unter Aussendung i) eines Photons oder ii) eines Positrons und eines Neutrinos.

Auch wenn der Potentialbegriff für die Starke Wechselwirkung streng genommen nicht zutreffend ist, darf man sich zur Veranschaulichung einen gemeinsamen Potentialtopf für die Nukleonen vorstellen.

Zunächst wird unterscheiden zwischen der initial aufzuwenden Energie zur Überwindung eines Potentialwalls und der Bindungsenergie. Für den Potentialnullpunkt = 0 im Unendlichen, einem Potentialwall > 0 sowie einen Potentialtopf mit Tiefe < 0 müssen die beiden Teilchen - aus dem Unendlichen kommend - den Potentialwall überwinden oder durchtunneln; anschließend nehmen sie gebundene Zustände bei E < 0 im gemeinsamen Potentialtopf ein. Für die Bindungsenergie = Energienullpunkt im Unendlichen minus Tiefe des Energieniveaus ist der Potentialwall irrelevant.

Dann existieren auch Fälle, bei denen aus derartigen Reaktionen keine gebundenen Zustände resultieren: bei schweren Kernen folgt aus der Starken Wechselwirkung kein anziehendes Potential; bei ungeeigneten Kombinationen von Spin und Isospin einzelner Nukleonen folgt ebenfalls kein anziehendes Potential; für ein Di-Proton dominiert das stark abstoßende Coulomb-Potential; für das Di-Neutron existiert bei geeigneter Kombinationen von Spin und Isospin zwar ein schwach anziehendes Potential, das jedoch zu flach ist um gebundene Zustände auszubilden (klassisch nicht erklärbar). Diese Themen werden im Folgenden nicht betrachtet ...

... übrig bleiben Fälle, die man analog zur Atomphysik diskutieren kann, siehe

In beiden Fällen wird Energie frei, die in die kinetischen Energie der entstehende Reaktionspartner eingeht, d.h. in das Deuteron und das Photon.

Im letzten Fall muss zunächst die Coulomb-Abstoßung überwunden werden, die anziehende Kernkraft überwiegt jedoch die abstoßende Coulombkraft.

TomS · Moderator Anmeldungsdatum: 20.03.2009 Beiträge: 18067

Die Bindungsenergie, ein Maß für die Stabilität des entstehenden gebundenen Systems stammt aus der Ruheenergie des vor dem Prozess ungebunden Teilchenpaares z.B. aus Proton und Neutron.

Wenn man das Deuteron D zunächst ohne seine Entstehungsgeschichte betrachtet, dann findet man zunächst eine Masse m_D. Betrachtet man Proton p und Neutron n isoliert, so hat man eine Gesamtmasse m_p + m_n.

Da nun D gebunden ist, ist die Masse m_D kleiner als die Summe der Massen m_p + m_n, d.h. beim Entstehen von D aus p und n wird Energie frei; dies entspricht dem sogenannte Massendefekt, definiert als

Umgekehrt muss dieser Energiebetrag dem Deuteron zugeführt werden, um z.B. durch ein hochenergetisches Photon das Deuteron wieder in Proton und Neutron aufzubrechen; daher spricht man von Bindungsenergie.

Konkrete Rechnung für

Gemäß Energieerhaltung folgt für den betrachteten Prozess

Ganz allgemein gilt für die Gesamtenergie E, Ruhemasse m und Impulsbetrag p der Zusammenhang

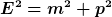
Seien p und n in Ruhe, d.h. ihre Impulse Null; außerdem hat das Photon Ruhemasse Null:

Einsetzen liefert

Wegen der Impulserhaltung hat D den exakt entgegengesetzten Impuls zu gamma, d.h.

Insgesamt folgt

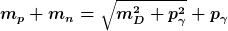
Der Wert von p_gamma ist nicht negativ, er entspricht exakt der Energie des Photons.

Wenn p_gamma exakt Null wäre - was letztlich bedeutet, dass kein Photon existiert - dann wäre

d.h. das System bliebe ungebunden.

Allgemein erhält man durch Umformen

Da die Ruhemassen von p und n größer Null sind, gilt das Gleichheitszeichen genau dann, wenn der Impuls verschwindet - s.o.

Andernfalls ist sicher

d.h. das ungebundene System aus zwei Einzelteilchen Proton p und Neutron n hat mehr Masse bzw. Ruheenergie als das gebundene Deuteron D.