| Autor |
Nachricht |
Till Nikolas
Anmeldungsdatum: 28.01.2021
Beiträge: 7
|
 Till Nikolas Verfasst am: 28. Jan 2021 00:09 Titel: Was genau ist die Bindungsenergie? Till Nikolas Verfasst am: 28. Jan 2021 00:09 Titel: Was genau ist die Bindungsenergie? |
 |
|
Meine Frage:
Hallo, ich frage mich, was genau die Bindungsenergie sein soll? Online stoße ich auf die Aussage, dass dies die Energie sei, die frei wird, wenn man aus einzelnen Protonen und Neutronen einen Kern "zusammenbaut". Mir ist bewusst, dass das Endprodukt eine geringere Masse aufweist, als die einzelnen Nukleonen des Kerns im ungebundenen Zustand. Doch warum? Wobei handelt es sich bei dieser mysteriösen freiwerdenden Energie? Wo kommt diese her?
Der Kern wird aufgrund der starken Wechselwirkung (durch den Austausch von Gluonen oder Quark-Antiquark-Paaren) zusammengehalten. Einige Internetseiten behaupten, dass Energie aufgrund der Anziehenden Kräfte im Kern verloren ginge(Zitat "Aufgrund der anziehenden Kräfte, verliert das System an Energie"). Heißt das etwas, die starke Wechselwirkung verbraucht Energie? Und wenn die starke Wechselwirkung tatsächlich Energie verbrauchen würde, warum würde dann Energie nach einer Kernfusion freiwerden?
Einzelne Nukleonen haben keine Bindungsenergie. Wenn sie zu einem Kern zusammengefügt werden, haben sie plötzlich eine Bindungsenergie. Zwischen welchen Instanzen wirkt die Bindungsenergie? Wodurch entsteht sie? Und vor Allem: Wo kommt sie her?
Meine Ideen:
Ich bin leider ein wenig ratlos und finde zu diesem Thema auch keine vertiefenden Literatur. In allen Büchern und auf allen Internetseiten stehen dieselben oberflächlichen Aussagen. Ich hoffe, jemand kann mir bei meiner Frage weiterhelfen? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 28. Jan 2021 01:44 Titel: TomS Verfasst am: 28. Jan 2021 01:44 Titel: |
 |
|
Fangen wir ganz einfach an.
Wenn sich ein Elektron mit kinetischer Energie > 0 Null und (in sehr großer Entfernung) potentieller Energie ~ 0 auf einen positiv geladenen Atomkern zubewegt, dann kann es von diesem nach den Regeln der Quantenmechanik eingefangen werden. Es geht in einen gebundenen Zustand mit Gesamtenergie < 0 im Coulombpotential des Kerns über.
Für das Elektron gilt also

Die Energiedifferenz

wird in Form eines Photons frei.
Umgekehrt kann ein Photon passender Energie von diesem gebundenen Elektron absorbiert werden. Bei genügend hoher Energie des Photons wird das Atom ionisiert, das Elektron wieder frei. Wenn das Elektron in einem Zustand E < 0 gebunden ist, dann entspricht die Energiedifferenz zu E’ = 0, d.h.
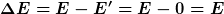
gerade der Ionisierungs- bzw. Bindungsenergie. Das Elektron wäre nach Absorption eines Photons dieser Energie in einem Zustand E’ = 0, der gerade die Grenze zwischen freien und gebundenen Elektronen darstellt.
In diesem Fall stammt die Bindungsenergie aus dem gemeinsamen Feld von Elektron und Atomkern.
Eine typische Größenordnung in der Atomphysik sind einige 10 eV, die Masse des Elektrons entspricht jedoch 511 keV, d.h. die Bindungsenergie ist extrem klein ggü. der Masse des Elektrons (und erst recht ggü. der des Atomkerns) so dass in der Atomphysik der entsprechende Massendefekt zumeist vernachlässigt wird. In der Kern- und Teilchenphysik ist der Massendefekt bezogen auf die Massen der beteiligten Teilchen deutlich größer.
Wenn das soweit klar ist, können wir Nukleonen und Kerne diskutieren.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Till Nikolas
Anmeldungsdatum: 28.01.2021
Beiträge: 7
|
 Till Nikolas Verfasst am: 28. Jan 2021 11:08 Titel: Aber wie sieht es in der Kernphysik aus? Till Nikolas Verfasst am: 28. Jan 2021 11:08 Titel: Aber wie sieht es in der Kernphysik aus? |
 |
|
Danke erstmal für die schnelle Antwort. Was die Bindungsenergie im Bereich der Atomphysik bedeutet ist mir weitestgehend klar. Was ich nicht ganz verstehe, ist was genau die Bindungsenergie in der Kernphysik sein soll. Allein der Name impliziert, dass es sich hierbei um eine Energie handelt, die etwas zusammenbindet?
"In der Kernphysik ist die Bindungsenergie die Energiemenge, die aufgewandt werden muss, um den Atomkern in seine Nukleonen zu zerlegen.[5] Umgekehrt wird eine ebenso große Energie frei, wenn sich Nukleonen zu einem Kern vereinigen." (Wikipedia - Bindungsenergie)
Wieso wird Energie frei, wenn sich Nukleonen zu eine Kern vereinen? Wer gibt diese Energie ab? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 28. Jan 2021 12:23 Titel: TomS Verfasst am: 28. Jan 2021 12:23 Titel: |
 |
|
Letztlich verhält es sich ganz ähnlich wie im Falle der Atomphysik.
Das Potential hat nicht die Form eines Coulomb-Potentials, die Nukleonen übernehmen die Rolle von Elektron und Atomkern, das Photon wäre ein hochenergetisches gamma-Quant.
Stimmt die Aussage “was die Bindungsenergie im Bereich der Atomphysik bedeutet ist mir weitestgehend klar” wirklich?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 28. Jan 2021 12:25 Titel: TomS Verfasst am: 28. Jan 2021 12:25 Titel: |
 |
|
Letztlich verhält es sich ganz ähnlich wie im Falle der Atomphysik.
Das Potential hat nicht die Form eines Coulomb-Potentials, die Nukleonen übernehmen die Rolle von Elektron und Atomkern; das Photon wäre ein hochenergetisches gamma-Quant.
Stimmt die Aussage “was die Bindungsenergie im Bereich der Atomphysik bedeutet ist mir weitestgehend klar” wirklich?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Till Nikolas
Anmeldungsdatum: 28.01.2021
Beiträge: 7
|
 Till Nikolas Verfasst am: 28. Jan 2021 12:37 Titel: Till Nikolas Verfasst am: 28. Jan 2021 12:37 Titel: |
 |
|
Sagen wir es so: Ich verstehe die grundlegende Idee hinter der Bindungsenergie in der Atomphysik. Ich kenne die Ionisierungsenergie, das Anregen von Atomen durch Photonabsorption und habe ein Grundverständnis von den Energiezniveaus im Atom.
Ich verstehe demnach, dass man einen Kern in seine Nukleonen zerlegen kann, wenn man ihm die Bindungsenergie hinzufügt. Das kann ich logisch nachvollziehen.
Was ich nicht verstehe, ist warum Energie frei wird, wenn sich Nukleonen zu einem Kern zusammenfügen. (Es gibt einen Massendefekt und daraus kann man die Bindungsenergie berechnen, aber das erklärt nicht, warum überhaupt Energie freiwird? Sollte nich eher Energie für den Zusammenschluss der Nukleonen verbraucht werden? (das scheint ja nur bei der Kernfusion sehr großer Kerne der Fall zu sein)
Daher würde ich eigentlich annehmen, dass Energie aufgebracht werden muss, um die Coulomb Kraft zwischen den Nukleonen zu überwinden, sodass es zu einer Kernfusion kommen kann. Jetzt höre ich, dass dabei eher Energie entsteht (bei kleinen Kernen). Daher die Frage: Wo kommt diese freiwerdende Energie her? Wer gibt sie ab? |
|
 |
Füsik-Gast
Gast
|
 Füsik-Gast Verfasst am: 28. Jan 2021 14:02 Titel: Strong force Füsik-Gast Verfasst am: 28. Jan 2021 14:02 Titel: Strong force |
 |
|
In der Atomphysik betrachtet man die elektrostatische Wechselwirkung zwischen Elektronen und Atomkern.
In der Kernphysik gibt es die Elektrostatik für die Annäherung gleichartig geladener Teilchen,den Protonen.Sobald die dabei relevante Coulomb-Barriere überwunden ist,greifen die Kernkräfte zwischen den Nukleonen,ungeachtet deren Ladungen.
Dabei wirken die sog. "starken (Kern)kräfte".
Der Energiegewinn beim Zusammenfügen ist bei kleinen Kernen recht groß,
nimmt dann in Richtung schwerer Kerne ab.
Für detailiertere Erklärungen zu den starken Kräften und den Bindungsenergien werden hier sicherlich kompetentere Beiträge noch kommen.
Füsik-Gast. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 28. Jan 2021 14:08 Titel: TomS Verfasst am: 28. Jan 2021 14:08 Titel: |
 |
|
Zunächst mal musst du unterscheiden zwischen der initial aufzuwenden Energie zur Überwindung eines Potentialwalls und der Bindungsenergie. Nimm den Potentialnullpunkt bei E=0, üblicherweise in unendlicher Entfernung, dann einen Potentialwall mit E>0 sowie einen Potentialtopf mit E<0. Aus dem Unendlichen kommend musst du den Potentialwall überwinden (oder durchtunneln), zuletzt fällt das Teilchen in den Topf. Für die Bindungsenergie = Energienullpunkt im Unendlichen minus Tiefe des Energieniveaus im Topfes ist der Potentialwall irrelevant.
Dann vergiss mal die Fälle, in denen eben keine gebundenen Zustände resultieren. Wenn du zwei schwere Kerne zusammenbringen möchtest, dann musst du zunächst Energie aufwenden um die Abstoßung zu überwinden, zudem ist theoretisch gedachte Kern ist instabil und zerfällt sofort wieder; d.h. es existiert kein Topf oder er ist zu flach. Hier zeigt sich lediglich, dass die Idee eines einfachen Potentialtopfes für die Kernkräfte nicht mehr anwendbar ist (können wir später diskutieren *)
Was übrig bleibt sind die Fälle, die du analog zur Atomphysik diskutieren kannst:
Einfang eines zunächst freien Elektrons im gemeinsamen Potentialtopf (Coulomb-Potential) von Elektron und Proton mit Entstehung eines neutralen Wasserstoffatoms unter Aussendung eines Photons.

Einfang (Fusion) von Proton und Neutron im gemeinsamen Potentialtopf (Kernkräfte) mit Entstehung eines Deuterons unter Aussendung eines Photons (mit typischerweise sehr hoher Energie)

Einfang (Fusion) von Proton und Proton im gemeinsamen Potentialtopf (Kernkräfte) mit Entstehung eines Deuterons unter Aussendung eines Positrons und eines Neutrinos

... u.v.a.m.
In allen Fällen wird Energie frei, die in der kinetischen Energie der Reaktionspartner steckt. Im letzten Fall muss zunächst die Coulomb-Abstoßung überwunden werden, aber die anziehende Kernkraft überwiegt letztlich die abstoßende Coulombkraft.
Die drei Fälle laufen analog, die Unterschiede stecken im wesentlichen in den Details, insbs. auch die Frage nach der genauen Form des Potentials einschließlich der Frage, ob die Wechselwirkung überhaupt anziehend oder abstoßend ist (siehe wieder *)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Till Nikolas
Anmeldungsdatum: 28.01.2021
Beiträge: 7
|
 Till Nikolas Verfasst am: 28. Jan 2021 17:18 Titel: Till Nikolas Verfasst am: 28. Jan 2021 17:18 Titel: |
 |
|
Ich verstehe, dass die Kernfusion von verschiedenen Faktoren abhängt. Für kleine Kerne (zum Beispiel Deuterium und Tritium) ist die Coulombbarriere sehr gering, weil nur zwei Protonen vorliegen. Nach der Überwindung dieser Barriere kommt die starke Wechselwirkung zum Zuge und Deuterium und Tritium fusionieren zu einem Heliumkern(4He) und einem Neutron. Dabei wird Energie frei.
Nun die Frage, warum diese freiwerdende Energie den Namen Bindungsenergie trägt? Handelt es sich hierbei lediglich um die freiwerdende kinetische Energie der beiden Ausgangskerne?
Da ist noch eine Lücke in diesem Rätsel. Irgendetwas muss mit der kinetischen Energie passieren, dass sie letztlich nach der abgeschlossenen Fusion freigesetzt wird. Wird sie nicht mehr benötigt? |
|
 |
Füsik-Gast
Gast
|
 Füsik-Gast Verfasst am: 28. Jan 2021 17:31 Titel: Bindungsenergie Füsik-Gast Verfasst am: 28. Jan 2021 17:31 Titel: Bindungsenergie |
 |
|
Die freiwerdende Energie entspricht vom Betrag her eben der Mindestenergie,die benötigt wird,um diese Bindung wieder aufzuheben,nach der Definition für Bindungsenergien allgemein.
Das gilt auf molekolarer,wie auch auf atomarer,nuklearer Ebene.
Je nach dem,welchen Prozeß du betrachtest,das Zusammenfügen(Bildung der Bindng) oder die Dissoziation(Spaltung der Bindung),ist das Vorzeichen für die Energie zu wählen.
Füsik-Gast. |
|
 |
Till Nikolas
Anmeldungsdatum: 28.01.2021
Beiträge: 7
|
 Till Nikolas Verfasst am: 28. Jan 2021 17:35 Titel: Till Nikolas Verfasst am: 28. Jan 2021 17:35 Titel: |
 |
|
|
ABER WO KOMMT DIE BINDUNGSENERGIE HER? Handelt es sich hierbei um die verlbliebene kinetische Energie der Anfangskerne? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 28. Jan 2021 18:17 Titel: TomS Verfasst am: 28. Jan 2021 18:17 Titel: |
 |
|
| Till Nikolas hat Folgendes geschrieben: | | Nun die Frage, warum diese freiwerdende Energie den Namen Bindungsenergie trägt? Handelt es sich hierbei lediglich um die freiwerdende kinetische Energie der beiden Ausgangskerne? |
Ist die obige Erklärung so unklar?
Bei einem Prozess, bei dem aus A und B ein gebundener, stabiler Zustand d.h. insbs. ein Kern C entsteht sowie ggf. weitere Teilchen x wie z.B.

wird Energie frei, die in der kinetischen Energie der entstehenden Teilchen steckt. Wenn ich C wieder in A und B aufbrechen möchte, muss ich mindestens diese Energie reinstecken, damit C in A und B aufgebrochen wird. Diese Energie misst also sozusagen die Festigkeit der Bindung von C und wird daher Bindungsenergie genannt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Till Nikolas
Anmeldungsdatum: 28.01.2021
Beiträge: 7
|
 Till Nikolas Verfasst am: 28. Jan 2021 20:36 Titel: Till Nikolas Verfasst am: 28. Jan 2021 20:36 Titel: |
 |
|
Ahh, verstehe. Aus der Betrachtungsweise macht der Name durchaus Sinn.
Noch eine letzte Frage:
Stammt die Bindungsenergie von den Teilchen A und B, oder vom Endprodukt C? DasZitat "wird Energie frei, die in der kinetischen Energie der entstehenden Teilchen steckt." impliziert, dass die Bindungsenergie aus dem Endprodukt C stammt. Verstehen ich das richtig? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 28. Jan 2021 22:18 Titel: TomS Verfasst am: 28. Jan 2021 22:18 Titel: |
 |
|
| Till Nikolas hat Folgendes geschrieben: | | Stammt die Bindungsenergie von den Teilchen A und B, oder vom Endprodukt C? Das Zitat "wird Energie frei, die in der kinetischen Energie der entstehenden Teilchen steckt." impliziert, dass die Bindungsenergie aus dem Endprodukt C stammt. |
Das besagt lediglich, dass die frei werdende Energie ja irgendwo hin muss. Es wird ein bisschen Masse (Ruhenergie) des System "A + B" in kinetische Energie des Systems "C + x" umgewandelt.
Die Energie stammt aber aus dem System "A + B", in gewisser Weise eben aus den Massen bzw. Ruheenergien.
A + B bilden - solange sie genügend weit voneinander entfernt sind - ein ungebundenes System. Wenn sie nahe genug zusammen, kommen bilden sie einen gebunden Zustand C, in dem die Individualität von A und B mehr oder weniger verloren geht.
Wenn man dieses C ohne seine Entstehungsgeschichte betrachtet, dann findet man zunächst eine Masse m_C.
Betrachtet man A + B isoliert, so hat man eine Gesamtmasse m_A + m_B.
Wenn nun C gebunden ist, dann ist die Masse m_C kleiner als die Summe der Massen m_A + m_B, d.h. beim Entstehen von C wird Energie frei, die "aus A + B stammt".
Konkrete Rechnung für

Ganz allgemein gilt für die Gesamtenergie E, Ruhemasse m und Impulsbetrag p der Zusammenhang
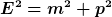
Gemäß Energieerhaltung folgt

Seien A und B vorher in Ruhe, d.h. ihre Impulse seien Null:


Wenn x ein Photon mit Ruhemasse Null ist, dann gilt außerdem


Einsetzen liefert

Wegen der Impulserhaltung hat C den exakt entgegengesetzten Impuls, d.h.

Insgesamt folgt

Der Wert von p_x ist nicht negativ, er entspricht ja der Energie des Photons.
Wenn p_x exakt Null ist - was letztlich bedeutet, dass kein Photon existiert - dann folgt sofort

Das System ist und bleibt ungebunden.
Allgemein erhält man durch Umformen
 - p_x\big]^2 = (m_A + m_B)^2 - 2\,p_x\,(m_A + m_B) +p_x^2)
^2 = - 2\,p_x\,(m_A + m_B) \le 0)
Da die Ruhemassen von A und B größer Null sind, gilt das Gleichheitszeichen genau dann, wenn der Impuls verschwindet.
Andernfalls ist sicher
^2 < 0)
d.h. das ungebundene System aus zwei Einzelteilchen A und B hat mehr Masse bzw. Ruheenergie als das gebundene System C.
PS.: der Massendefekt ist definiert als
)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Till Nikolas
Anmeldungsdatum: 28.01.2021
Beiträge: 7
|
 Till Nikolas Verfasst am: 29. Jan 2021 10:45 Titel: Till Nikolas Verfasst am: 29. Jan 2021 10:45 Titel: |
 |
|
|
Perfekt! Das bringt es auf den Punkt. Vielen Dank! |
|
 |
|
|















