| Autor |
Nachricht |
gnt
Gast
|
 gnt Verfasst am: 21. Jul 2018 18:23 Titel: Gaußsches Gesetz, Topologie, diskreter Raum |
 |
|
Hallo allerseits,
könntet Ihr mir hier bitte etwas auf die Sprünge helfen:
Es wird doch auch experimentell (Herleitung z.B. aus der Stringtheorie) untersucht, ob es bei kurzen Entfernungen Abweichungen vom 1/r-Potential gibt. Ist so etwas rein Folge der Topologie, evtl. abhängig von der Ausdehnung kompakter Dimensionen, oder steckt da mehr dahinter?
Konkret würde mich sowohl für einen kontinuierlichen, als auch vor allem einen diskreten Raum ("schachbrettartig", also eigentlich nichts anderes als Felder mit diskreten statt kontinuierlichen Koordinaten), im Fall von kompakten Dimensionen, interessieren, wie ein Vektorfeld aussieht, wenn man zu den drei normalen Raumdimensionen, eine oder mehrere Dimensionen hinzu fügt.
Im Fall eines offenen Universums mit kontinuierlichen Koordinaten ist mir die Lösung bekannt.
Gruß
gnt |
|
 |
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18078
|
| TomS Verfasst am: 22. Jul 2018 15:30 Titel: Re: Gaußsches Gesetz, Topologie, diskreter Raum |
|
|
| gnt hat Folgendes geschrieben: | Es wird doch auch experimentell (Herleitung z.B. aus der Stringtheorie) untersucht, ob es bei kurzen Entfernungen Abweichungen vom 1/r-Potential gibt. Ist so etwas rein Folge der Topologie, evtl. abhängig von der Ausdehnung kompakter Dimensionen, oder steckt da mehr dahinter?
|
Dahinter steckt zunächst die Topologie, jedoch zusätzlich Details der Geometrie.
Einfaches Beispiel: wir betrachten im Rahmen der Elektrostatik das elektrische Potential als Lösung der Poissongleichung
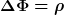
Zur Invertierung dieser Differentialgleichung kann man die Greensche Funktion konstruieren; diese entspricht letztlich dem Potential einer Punktladung. Offensichtlich hängt diese Lösung von der Dimension n ≥ 3 der zugrundeliegenden räumlichen Mannigfaltigkeit ab:
 = \frac{1}{(n-2)S^{(n)}} \frac{1}{r^{n-2}})
Für n =1 bzw. 2 findet man dagegen einen linearen bzw. logarithmischen Verlauf.
Darüberhinaus ergeben sich Unterschiede für gleiches n, jedoch unterschiedliche Topologien, z.B. für die n-Ebene und den n-Torus; das bekannte 1/r Verhalten im 3-dim. euklidischen Raum kann schon alleine aufgrund der Topologie für den ebenfalls flachen n-Torus nicht gelten.
Betrachtet man darüberhinaus gekrümmte Mannigfaltigkeiten, so muss die o.g. Poissongleichung modifiziert werden; der Differentialoperator muss die lokale Geometrie respektieren. Dies gilt z.B. für den Laplace-Beltrami-Operator
für eine Metrik sowie deren Determinante g.
Für die Stringtheorie kommen diverse Komplikationen hinzu, die Grundideen sind jedoch die oben beschriebenen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
gnt
Gast
|
| gnt Verfasst am: 22. Jul 2018 17:19 Titel: |
|
|
Vielen Dank für Deine Antwort!
Gekrümmte Räume wollte ich jetzt gar nicht betrachten, sondern nur auf ganz einfachem Niveau eine Überlegung führen: Wenn man weiß, dass makroskopisch zumindest näherungsweise ein 1/r-Potential gilt, und dass man 3 Dimensionen beobachtet, ist es dann möglich, dass es eine oder mehrere zusätzliche räumliche Dimensionen (gerne auch mit einer Ausdehnung von nur einer Planck-Länge) geben könnte, ohne dass sich diese auch makroskopisch wesentlich auf das 1/r-Potential auswirken, aber im Abstand der Größenordnung der Ausdehnung der Zusatzdimensionen bemerkbar machen? - Ich vermute, dass das zumindest bei Feldern nicht möglich ist - bei einem Punktteilchenstrom sähe das wohl anders aus.
Und die gleiche Überlegung habe ich für Felder mit diskreten Feldkoordinaten angestellt; da ist es noch schwieriger, aber es gibt keine Singularität. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18078
|
| TomS Verfasst am: 22. Jul 2018 17:48 Titel: |
|
|
| gnt hat Folgendes geschrieben: | | Gekrümmte Räume wollte ich jetzt gar nicht betrachten ... |
D.h. du betrachtest z.B. den 3-dim. euklidischen Raum mit weiteren d flachen und kompakten Zusatzdimensionen, z.B. die 3+d dimensionale Mannigfaltigkeit
| gnt hat Folgendes geschrieben: | | Wenn man weiß, dass makroskopisch zumindest näherungsweise ein 1/r-Potential gilt, und dass man 3 Dimensionen beobachtet, ist es dann möglich, dass es eine oder mehrere zusätzliche räumliche Dimensionen geben könnte, ohne dass sich diese auch makroskopisch wesentlich auf das 1/r-Potential auswirken, aber im Abstand der Größenordnung der Ausdehnung der Zusatzdimensionen bemerkbar machen? |
Dazu muss man z.B. die o.g. Greensfunktion des Laplaceoperators auf dieser 3+d dimensionale Mannigfaltigkeit konstruieren. Ich muss mir das mal im Detail ansehen, aber das Ergebnis sollte klar sein; makroskopisch erwartet man wieder 1/r, Abweichungen davon erst bei Längenskalen im Bereich der d kompakten Dimensionen oder darunter.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
gnt
Gast
|
| gnt Verfasst am: 22. Jul 2018 18:18 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | gnt hat Folgendes geschrieben: | | Gekrümmte Räume wollte ich jetzt gar nicht betrachten ... |
D.h. du betrachtest z.B. den 3-dim. euklidischen Raum mit weiteren d flachen und kompakten Zusatzdimensionen, z.B. die 3+d dimensionale Mannigfaltigkeit
|
Ja.
| TomS hat Folgendes geschrieben: | | gnt hat Folgendes geschrieben: | | Wenn man weiß, dass makroskopisch zumindest näherungsweise ein 1/r-Potential gilt, und dass man 3 Dimensionen beobachtet, ist es dann möglich, dass es eine oder mehrere zusätzliche räumliche Dimensionen geben könnte, ohne dass sich diese auch makroskopisch wesentlich auf das 1/r-Potential auswirken, aber im Abstand der Größenordnung der Ausdehnung der Zusatzdimensionen bemerkbar machen? |
Dazu muss man z.B. die o.g. Greensfunktion des Laplaceoperators auf dieser 3+d dimensionale Mannigfaltigkeit konstruieren. Ich muss mir das mal im Detail ansehen, aber das Ergebnis sollte klar sein; makroskopisch erwartet man wieder 1/r, Abweichungen davon erst bei Längenskalen im Bereich der d kompakten Dimensionen oder darunter. |
Hmm. Die kompakte Dimension erfordert eine Gesamtladung 0 - wie der eindimensionale Fall. Wenn ich das richtig sehe, müsste, wenn x Element R und y Element T ist, die Gesamtladung auch für jedes x immer Null sein. Es müsste also für eine positive Ladung bei x=3 auch eine negative bei x=3 mit jeweils beliebigem y vorhanden sein. Dann könnten vermutlich makroskopisch gar keine Ladungen festgestellt werden.
 |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18078
|
| TomS Verfasst am: 22. Jul 2018 19:14 Titel: |
|
|
Nehmen wir stattdessen
mit 3 großen und d kleinen Dimensionen. Gegeben seien die Koordinaten
;\; i = 1..3, a =1..d)
Auf diesem Torus gilt Translationsinvarianz
 = f(x+\ell\hat{e}^i) )
für alle Objekte wie z.B. Funktionen, Operatoren etc.
Betrachte den 3+d Laplacian
mit dem Eigenwertproblem
sowie der Greenschen Funktion
 = \sum_\lambda \lambda^{-1} \, u_\lambda(x) \, u^\ast_\lambda(y))
Ohne die Inverse des Eigenwertes führt die Summe auf die delta-Distribution.
Offenbar müssen die Eigenfuntionen die o.g. Bedingung der Translationsinvarianz erfüllen. Damit erfüllen auch die Greensche Funktion sowie die delta-Distribution die Bedingung der Translationsinvarianz.
Das Verschiwnden der Gesamtladung lautet ja
Dabei ist jedoch eine nicht-verschwindende Ladungsdichte, z.B. als Summe von delta-Funktionen erlaubt, d.h.
}(x-x_q)\delta^{(d)}(\xi-\xi_q))
In einem 3-Bereich V, der eine einzige Ladung q enthält gilt jedoch
}(x-x_q)\delta^{(d)}(\xi-\xi_q) = \int_V \dd^3x \, q\,\delta^{(3)}(x-x_q) = q)
Das xi-Integral liefert dabei immer einen Beitrag, da über die gesamten d-Torus integriert wird, während das x-Integral nur dann einen Beitrag liefert, wenn das gewählte 3-Volumen V auch eine Ladung enthält.
Offenbar ist es makroskopisch egal, wo auf dem d-Torus die Ladung sitzt, während es von erheblicher Relevanz ist, wo auf dem 3-Torus die Ladung sitzt. Wir mitteln hier sozusagen über den d-Torus.
Nochmal zurück zum Laplacian. Das Eigenwertproblem führt mittels Separationsansatz auf gewöhnliche ebene Wellen. D.h. man findet in der Summe zur Darstellung der Greensfunktion Terme der Form
} (\vec{x},\vec{\xi}) = \exp[{2\pi i \vec{n}\vec{x}/L}] \, \exp[{2\pi i \vec{\nu}\vec{\xi}/\ell}] )
Der Fall ohne Extradimensionen entspricht gerade
d.h. dem Fall, dass in den Extradimensionen keine Oszillationen vorliegen.
Das Hinzunehmen der Oszillationen in den Extradimensionen wird auch dem Verlauf der Greenschen Funktion in den 3 großen Dimensionen eine Signatur aufprägen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 24. Jul 2018 07:09, insgesamt einmal bearbeitet |
|
|
gnt
Gast
|
| gnt Verfasst am: 23. Jul 2018 18:08 Titel: |
|
|
Danke für die Erklärung.
Ich habe etliche Stunden lang versucht, das für den Fall 3+1 zu berechnen, war aber leider total erfolglos - es treten Unendlichkeiten auf.
Ich glaube jetzt, dass man sich die Abstandsabhängigkeit grob so vorstellen kann, dass eine modifizierte Norm gilt, in der die kleinen Dimensionen nur im Nahbereich ins Gewicht fallen, eben weil diese so "kurz" sind. |
|
|
|
|
Registrieren
Login
FAQ
Suchen
