| Autor |
Nachricht |
gnt
Gast
|
 gnt Verfasst am: 15. Aug 2017 11:28 Titel: QED Formeln gnt Verfasst am: 15. Aug 2017 11:28 Titel: QED Formeln |
 |
|
Hallo allerseits,
ich versuche, die QED etwas zu verstehen, bin aber von Weinbergs Buch noch immer völlig erschlagen. Deshalb möchte ich jetzt erst einmal die Bewegungsgleichungen der QED analysieren.
Mit der Dirac-Gleichung komme ich inzwischen klar, aber die genauen Formen von psi und A sind mir noch rätselhaft. Zwar habe ich dafür in den Herleitungen in Weinbergs Buch Ausdrücke gefunden, aber die kann ich nicht vollständig interpretieren.
Gibt es denn dafür eine Art Formelsammlung, in der alle Formelbestandteile beschrieben werden, ohne mich durch diese extrem mathematischen Herleitungen kämpfen zu müssen?
Z.B. hier
=(2\pi)^{-3/2}\sum_\sigma \int d^3 p [u_l(p,\sigma)e^{ipx}a(p,\sigma)+v_l(p,\sigma)e^{-ipx}a^{c \dagger}(p,\sigma)])
weiss ich nicht, wofür l und a stehen, und mir ist auch nicht klar, wie man von den Koeffizientenfunktionen mit Null Impuls zu einem bestimmten Impuls kommt - die Formel dafür sehe ich, aber die erscheint mir seltsam (wenn's die richtige ist...).
Bei A geht es mir ähnlich.
Ich hätte gerne einfach etwas, mit dem man zumindest theoretisch rechnen könnte, ohne abstraktes/für Laien, für nicht Mathematiker unverständliches.
Schon 'mal Danke!
Gruss |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 15. Aug 2017 13:05 Titel: index_razor Verfasst am: 15. Aug 2017 13:05 Titel: |
 |
|
Was genau möchtest du denn rechnen? Wenn du elementare QED-Prozesse ausrechnen möchtest, so wie e-e-Streuung z.B., dann brauchst du ein Buch, das möglichst direkt zu den Feynman-Regeln kommt. Der Peskin, Schröder ist so aufgebaut, mit einem Fokus auf QED in den ersten Kapiteln und einer sukzessiven Erweiterung zum Standardmodell der Elementarteilchen in den späteren. Ich glaube das Buch ist bei Studenten, die mit Teilchenphysik zu tun haben, allgemein recht beliebt.
Um zu versuchen deine Fragen noch zu beantworten: ) und und ) stehen für Vernichtungsoperatoren von Teilchen mit festem Impuls und Spin bzw. den Erzeugungsoperatoren der zugehörigen Anti-Teilchen. Im allgemeinen müssen Vernichter und Erzeuger von Teilchen-Anti-Teilchen-Paaren gemeinsam im Feld auftreten, damit die Prozesse der Theorie nichttriviale Erhaltungssätze erfüllen können. (Jeder Vertex im Feynman-Diagramm entsteht durch Vertauschung eines Teilchen-Erzeugers und eines Antiteilchen-Vernichters.) stehen für Vernichtungsoperatoren von Teilchen mit festem Impuls und Spin bzw. den Erzeugungsoperatoren der zugehörigen Anti-Teilchen. Im allgemeinen müssen Vernichter und Erzeuger von Teilchen-Anti-Teilchen-Paaren gemeinsam im Feld auftreten, damit die Prozesse der Theorie nichttriviale Erhaltungssätze erfüllen können. (Jeder Vertex im Feynman-Diagramm entsteht durch Vertauschung eines Teilchen-Erzeugers und eines Antiteilchen-Vernichters.)
Der Index 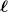 kommt einfach aus dem Lorentz-Transformtionsgesetz der Felder, d.h. im allgemeinen sind die Quantenfelder nicht invariant unter Lorentz-Transformationen, sondern bilden Tupel (Multiplets), von Komponenten, die beim Wechsel des Bezugssystems ineinander überführt werden. In der Sprache der Gruppentheorie handelt es sich bei den kommt einfach aus dem Lorentz-Transformtionsgesetz der Felder, d.h. im allgemeinen sind die Quantenfelder nicht invariant unter Lorentz-Transformationen, sondern bilden Tupel (Multiplets), von Komponenten, die beim Wechsel des Bezugssystems ineinander überführt werden. In der Sprache der Gruppentheorie handelt es sich bei den  also bei mehr als einer Komponente nicht mehr um skalare (triviale) Darstellungen der Lorentz-Gruppe, sondern um spinorielle oder vektorielle Darstellungen. also bei mehr als einer Komponente nicht mehr um skalare (triviale) Darstellungen der Lorentz-Gruppe, sondern um spinorielle oder vektorielle Darstellungen.
| Zitat: |
[...] wie man von den Koeffizientenfunktionen mit Null Impuls zu einem bestimmten Impuls kommt [...] |
Das funktioniert nur für massive Felder. Hierbei macht man sich die erwähnte Lorentz-Transformationseigenschaft der Felder zunutze. Das heißt, man erarbeitet erst die Form des Koeffizienten im Ruhesystem unter Ausnutzung des Transformationseigenschaften für Translation und Drehung, aber ohne ohne Wechsel des Inertialsystems. Dann benutzt man die Tatsache, daß ein massives Feld/Teilchen mit Impuls p nichts anderes als ein lorentz-transformiertes ruhendes Teilchen ist und wendet eine eintsprechende Lorentztransformation auf die Koeffizientenfunktionen an. |
|
 |
gnt
Gast
|
 gnt Verfasst am: 15. Aug 2017 13:35 Titel: gnt Verfasst am: 15. Aug 2017 13:35 Titel: |
 |
|
Vielen Dank für Deine Antwort!
| index_razor hat Folgendes geschrieben: | | Was genau möchtest du denn rechnen? |
Nichts spezielles. Es geht mir mehr um das Verständnis. Aber ich hätte eben gerne alles formelmässige vollständig vor mir, so dass man (vorausgesetzt es gibt oder gäbe die mathematischen Werkzeuge) alles berechnen könnte, und das nicht nur grob "skizziert". Mir ist schon bewusst, dass Physiker auch mit teils extrem kompakter Notation klar kommen, aber dafür muss man die Theorien eben schon durchdrungen haben.
| index_razor hat Folgendes geschrieben: | Um zu versuchen deine Fragen noch zu beantworten: ) und und ) stehen für Vernichtungsoperatoren von Teilchen mit festem Impuls und Spin bzw. den Erzeugungsoperatoren der zugehörigen Anti-Teilchen. stehen für Vernichtungsoperatoren von Teilchen mit festem Impuls und Spin bzw. den Erzeugungsoperatoren der zugehörigen Anti-Teilchen. |
Ja, schon, aber das ist ja nur die Bedeutung. Die sollen wohl auf den Hilbertraum wirken, nur wie tun sie das? Stehen da irgendwelche Ableitungen, Transformationen oder was auch immer drin?
| index_razor hat Folgendes geschrieben: | Der Index 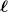 kommt einfach aus dem Lorentz-Transformtionsgesetz der Felder, d.h. im allgemeinen sind die Quantenfelder nicht invariant unter Lorentz-Transformationen, ... kommt einfach aus dem Lorentz-Transformtionsgesetz der Felder, d.h. im allgemeinen sind die Quantenfelder nicht invariant unter Lorentz-Transformationen, ... |
Steht das l hier einfach für die vier Einträge im Dirac-Spinor?
| index_razor hat Folgendes geschrieben: |
| Zitat: |
[...] wie man von den Koeffizientenfunktionen mit Null Impuls zu einem bestimmten Impuls kommt [...] |
Das funktioniert nur für massive Felder. Hierbei macht man sich die erwähnte Lorentz-Transformationseigenschaft der Felder zunutze. Das heißt, man erarbeitet erst die Form des Koeffizienten im Ruhesystem unter Ausnutzung des Transformationseigenschaften für Translation und Drehung, aber ohne ohne Wechsel des Inertialsystems. Dann benutzt man die Tatsache, daß ein massives Feld/Teilchen mit Impuls p nichts anderes als ein lorentz-transformiertes ruhendes Teilchen ist und wendet eine eintsprechende Lorentztransformation auf die Koeffizientenfunktionen an. |
Soweit habe ich das verstanden, jedoch komme ich mit der vermuteten Formel nicht klar. Ich habe hier z.B.:
=\sqrt{m/p^0}D(L(p))u(0,\sigma))
u(0,sigma) ist konstant, L(p) dürfte eine Lorentztransformation für den Impuls p sein, und D eine Matrix daraus machen, aber unter der Wurzel steht ein 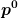 , und das ist doch die Gesamtenergie und damit H. Jetzt ist es aber doch so, dass u(p,sigma) in psi(x) eingesetzt, und auf das wiederum H wirkt, Wenn a die gesuchten Funktionen/Operatoren sind, dann würde doch H sich selbst beinhalten. Das wäre eine Rekursion. So wie ich das sehe, kann es also nicht sein. , und das ist doch die Gesamtenergie und damit H. Jetzt ist es aber doch so, dass u(p,sigma) in psi(x) eingesetzt, und auf das wiederum H wirkt, Wenn a die gesuchten Funktionen/Operatoren sind, dann würde doch H sich selbst beinhalten. Das wäre eine Rekursion. So wie ich das sehe, kann es also nicht sein. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 15. Aug 2017 15:23 Titel: jh8979 Verfasst am: 15. Aug 2017 15:23 Titel: |
 |
|
| gnt hat Folgendes geschrieben: |
Nichts spezielles. Es geht mir mehr um das Verständnis. Aber ich hätte eben gerne alles formelmässige vollständig vor mir, so dass man (vorausgesetzt es gibt oder gäbe die mathematischen Werkzeuge) alles berechnen könnte, und das nicht nur grob "skizziert". Mir ist schon bewusst, dass Physiker auch mit teils extrem kompakter Notation klar kommen, aber dafür muss man die Theorien eben schon durchdrungen haben.
|
In der QFT ist es in der Tat einfacher zu lernen wie man Sachen berechnet, als die Theorie dahinter wirklich zu verstehen. Ich würde Dir daher raten mit konkreten einfachen Berechnungen anzufangen. Hierzu eignet sich der Peskin&Schröder ziemlich gut, besonders wenn Du es Dir nur mit dem Buch selber beibringen willst.
Der Weinberg ist zwar das(!) beste QFT-Buch (auch seine anfangs merkwürdige Notation macht mehr Sinn, wenn man sich länger dam mit beschäftigt), ist aber nicht ganz einfach zu verstehen und zum ersten Mal QFT selber lernen eher schwierig.
| Zitat: |
| index_razor hat Folgendes geschrieben: | Um zu versuchen deine Fragen noch zu beantworten: ) und und ) stehen für Vernichtungsoperatoren von Teilchen mit festem Impuls und Spin bzw. den Erzeugungsoperatoren der zugehörigen Anti-Teilchen. stehen für Vernichtungsoperatoren von Teilchen mit festem Impuls und Spin bzw. den Erzeugungsoperatoren der zugehörigen Anti-Teilchen. |
Ja, schon, aber das ist ja nur die Bedeutung. Die sollen wohl auf den Hilbertraum wirken, nur wie tun sie das? |
Ja tun sie. Schau vllt mal hier:
https://de.wikipedia.org/wiki/Zweite_Quantisierung#Grundbegriffe
| Zitat: |
Soweit habe ich das verstanden, jedoch komme ich mit der vermuteten Formel nicht klar. Ich habe hier z.B.:
=\sqrt{m/p^0}D(L(p))u(0,\sigma))
u(0,sigma) ist konstant, L(p) dürfte eine Lorentztransformation für den Impuls p sein, und D eine Matrix daraus machen, aber unter der Wurzel steht ein 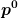 , und das ist doch die Gesamtenergie und damit H. Jetzt ist es aber doch so, dass u(p,sigma) in psi(x) eingesetzt, und auf das wiederum H wirkt, Wenn a die gesuchten Funktionen/Operatoren sind, dann würde doch H sich selbst beinhalten. Das wäre eine Rekursion. So wie ich das sehe, kann es also nicht sein. , und das ist doch die Gesamtenergie und damit H. Jetzt ist es aber doch so, dass u(p,sigma) in psi(x) eingesetzt, und auf das wiederum H wirkt, Wenn a die gesuchten Funktionen/Operatoren sind, dann würde doch H sich selbst beinhalten. Das wäre eine Rekursion. So wie ich das sehe, kann es also nicht sein. |
Richtig. Da steht ja auch p0 und nicht H. Die p's hier sind einfach ein ganz normaler Impuls, ganz normale Zahlen, kein Operator. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 15. Aug 2017 15:26 Titel: index_razor Verfasst am: 15. Aug 2017 15:26 Titel: |
 |
|
| gnt hat Folgendes geschrieben: |
Nichts spezielles. Es geht mir mehr um das Verständnis. Aber ich hätte eben gerne alles formelmässige vollständig vor mir, so dass man (vorausgesetzt es gibt oder gäbe die mathematischen Werkzeuge) alles berechnen könnte, und das nicht nur grob "skizziert". Mir ist schon bewusst, dass Physiker auch mit teils extrem kompakter Notation klar kommen, aber dafür muss man die Theorien eben schon durchdrungen haben.
|
Ich kann nicht ganz nachvollziehen, was du suchst. Einerseits fragst du nach einer "Formelsammlung", andererseits geht es dir ums Verständnis. Zuletzt wolltest du dich nicht durch die mathematischen Herleitungen kämpfen, jetzt willst du alles selbst berechnen und zwar nicht nur grob skizziert. Das klingt recht widersprüchlich. Das Problem ist glaube ich, daß der Weinberg einfach zu anspruchsvoll ist für den Einstieg. Die Behandlung des Themas ist sicher nicht skizzenhaft, aber es ist m.E. einfach ein schweres Buch. Hast du es mal mit einem anderen probiert?
| Zitat: |
| index_razor hat Folgendes geschrieben: | Um zu versuchen deine Fragen noch zu beantworten: ) und und ) stehen für Vernichtungsoperatoren von Teilchen mit festem Impuls und Spin bzw. den Erzeugungsoperatoren der zugehörigen Anti-Teilchen. stehen für Vernichtungsoperatoren von Teilchen mit festem Impuls und Spin bzw. den Erzeugungsoperatoren der zugehörigen Anti-Teilchen. |
Ja, schon, aber das ist ja nur die Bedeutung. Die sollen wohl auf den Hilbertraum wirken, nur wie tun sie das? Stehen da irgendwelche Ableitungen, Transformationen oder was auch immer drin?
|
Was für Ableitungen und Transformationen denn? Die Operatoren wirken auf dem Fockraum: Der Erzeuger ) erzeugt einen Zustand mit einem zusätzlichen Teilchen mit den Quantenzahlen erzeugt einen Zustand mit einem zusätzlichen Teilchen mit den Quantenzahlen  , also , also
|\psi\rangle = N_\psi |p,\sigma,n\rangle|\psi\rangle ) , ,
was auch immer 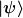 war. war. ) definiert man am besten als "Adjungierten" zu definiert man am besten als "Adjungierten" zu 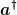 . Im Weinberg wird das alles lang und breit in Kapitel 4 erklärt. Allerdings gibt es wahrscheinlich wiederum bessere Einstiegslektüre, wenn du noch nie etwas vom Fockraum gehört hast. . Im Weinberg wird das alles lang und breit in Kapitel 4 erklärt. Allerdings gibt es wahrscheinlich wiederum bessere Einstiegslektüre, wenn du noch nie etwas vom Fockraum gehört hast.
| Zitat: |
| index_razor hat Folgendes geschrieben: | Der Index 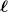 kommt einfach aus dem Lorentz-Transformtionsgesetz der Felder, d.h. im allgemeinen sind die Quantenfelder nicht invariant unter Lorentz-Transformationen, ... kommt einfach aus dem Lorentz-Transformtionsgesetz der Felder, d.h. im allgemeinen sind die Quantenfelder nicht invariant unter Lorentz-Transformationen, ... |
Steht das l hier einfach für die vier Einträge im Dirac-Spinor?
|
Zum Beispiel. Kommt drauf an. Es können auch Multipletts von solchen Spinoren sein oder auch nur mit zwei Einträgen entsprechend den Pauli-Matrizen. Es kann sich auch um 4er-Vektorindizes handeln, wie bei den W- und Z-Bosonen. Das hat alles mehr oder weniger damit zu tun, welchen Symmetrien die Theorie gehorcht, ob es sich um massive oder masselose Teilchen handelt, welchen Spin sie haben, etc.
| Zitat: |
Soweit habe ich das verstanden, jedoch komme ich mit der vermuteten Formel nicht klar. Ich habe hier z.B.:
=\sqrt{m/p^0}D(L(p))u(0,\sigma))
u(0,sigma) ist konstant, L(p) dürfte eine Lorentztransformation für den Impuls p sein, und D eine Matrix daraus machen, aber unter der Wurzel steht ein 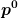 , und das ist doch die Gesamtenergie und damit H. , und das ist doch die Gesamtenergie und damit H.
|
L(p) ist nicht die Lorentz-Transformation "für" den Impuls, sondern eine (ich denke drehungsfreie) Lorentztransformation, die ein ruhendes Teilchen mit Masse m in ein bewegtes Teilchen mit Impuls p und Energie  überführt. überführt.
D ist die Darstellung dieser Transformation auf der Menge der Felder, also im Fall von Spinoren irgendwas mit e hoch Pauli-Matrizen, wenn ich mich nicht irre.
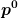 ist nicht die Gesamtenergie oder der Hamiltonoperator, sondern einfach die Energie eines freien massiven Teilchens mit Impuls p. ist nicht die Gesamtenergie oder der Hamiltonoperator, sondern einfach die Energie eines freien massiven Teilchens mit Impuls p. |
|
 |
gnt
Gast
|
 gnt Verfasst am: 15. Aug 2017 17:12 Titel: gnt Verfasst am: 15. Aug 2017 17:12 Titel: |
 |
|
Vielen Dank für Deine Antwort, jh8979!
Die erhöhen bzw. erniedrigen demnach den Eigenwert eines Zustands... Und nicht-abstrakt müsste das einer Multiplikation mit Kronecker- und Dirac-Deltas für die Eigenschaften des zu erzeugenden bzw. vernichtenden Teilchens entsprechen, richtig?
| jh8979 hat Folgendes geschrieben: |
| Zitat: |
Soweit habe ich das verstanden, jedoch komme ich mit der vermuteten Formel nicht klar. Ich habe hier z.B.:
=\sqrt{m/p^0}D(L(p))u(0,\sigma))
u(0,sigma) ist konstant, L(p) dürfte eine Lorentztransformation für den Impuls p sein, und D eine Matrix daraus machen, aber unter der Wurzel steht ein 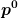 , und das ist doch die Gesamtenergie und damit H. Jetzt ist es aber doch so, dass u(p,sigma) in psi(x) eingesetzt, und auf das wiederum H wirkt, Wenn a die gesuchten Funktionen/Operatoren sind, dann würde doch H sich selbst beinhalten. Das wäre eine Rekursion. So wie ich das sehe, kann es also nicht sein. , und das ist doch die Gesamtenergie und damit H. Jetzt ist es aber doch so, dass u(p,sigma) in psi(x) eingesetzt, und auf das wiederum H wirkt, Wenn a die gesuchten Funktionen/Operatoren sind, dann würde doch H sich selbst beinhalten. Das wäre eine Rekursion. So wie ich das sehe, kann es also nicht sein. |
Richtig. Da steht ja auch p0 und nicht H. Die p's hier sind einfach ein ganz normaler Impuls, ganz normale Zahlen, kein Operator. |
Ah, gut, Danke!
Zuletzt bearbeitet von gnt am 15. Aug 2017 17:33, insgesamt 2-mal bearbeitet |
|
 |
gnt
Gast
|
 gnt Verfasst am: 15. Aug 2017 17:32 Titel: gnt Verfasst am: 15. Aug 2017 17:32 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | gnt hat Folgendes geschrieben: |
Nichts spezielles. Es geht mir mehr um das Verständnis. Aber ich hätte eben gerne alles formelmässige vollständig vor mir, so dass man (vorausgesetzt es gibt oder gäbe die mathematischen Werkzeuge) alles berechnen könnte, und das nicht nur grob "skizziert". Mir ist schon bewusst, dass Physiker auch mit teils extrem kompakter Notation klar kommen, aber dafür muss man die Theorien eben schon durchdrungen haben.
|
Ich kann nicht ganz nachvollziehen, was du suchst. Einerseits fragst du nach einer "Formelsammlung", andererseits geht es dir ums Verständnis. Zuletzt wolltest du dich nicht durch die mathematischen Herleitungen kämpfen, jetzt willst du alles selbst berechnen und zwar nicht nur grob skizziert. Das klingt recht widersprüchlich. |
Nein, finde ich nicht. ;-)
Anhand eines Beispiels aus der QM verdeutlicht, was ich meine: U(t,t0)|psi> wäre mir zu abstrakt, die mathematischen Eigenschaften des Operators U zu untersuchen, ist mir zu viel; beispielsweise wäre exp(-iHt)exp(...) das, was ich gerne sehen würde. So etwas für die Dirac-Gleichung etc. im Rahmen der QED würde es mir erlauben, die Dynamik und die Eigenschaften zu analysieren, und man könnte damit rechnen, aber das muss gar nicht sein - mir würde die Analyse reichen, einfach für's Verständnis, was da passiert.
Aber ein kleines Stückchen bin ich durch diesen Thread schon weiter.
| index_razor hat Folgendes geschrieben: | | Hast du es mal mit einem anderen probiert? |
Ja, ich habe schon auch ein anderes, aber in dem kriegt man die Feynmanregeln vorgesetzt, und dann wird damit gerechnet. Regeln ohne deren Sinn zu kennen abzuarbeiten finde ich frustrierend.
| index_razor hat Folgendes geschrieben: |
Was für Ableitungen und Transformationen denn? |
Ich dachte, dass auf solche Weise evtl. Teilchen erzeugt werden, aber offenbar sind das, wie oben vermutet, die Kronecker- und Dirac-Delta-Funktionen.
| index_razor hat Folgendes geschrieben: |
| Zitat: |
| index_razor hat Folgendes geschrieben: | Der Index 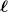 kommt einfach aus dem Lorentz-Transformtionsgesetz der Felder, d.h. im allgemeinen sind die Quantenfelder nicht invariant unter Lorentz-Transformationen, ... kommt einfach aus dem Lorentz-Transformtionsgesetz der Felder, d.h. im allgemeinen sind die Quantenfelder nicht invariant unter Lorentz-Transformationen, ... |
Steht das l hier einfach für die vier Einträge im Dirac-Spinor?
|
Zum Beispiel. Kommt drauf an. ... |
Gut, Danke! |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 16. Aug 2017 09:36 Titel: index_razor Verfasst am: 16. Aug 2017 09:36 Titel: |
 |
|
| gnt hat Folgendes geschrieben: |
Die erhöhen bzw. erniedrigen demnach den Eigenwert eines Zustands... Und nicht-abstrakt müsste das einer Multiplikation mit Kronecker- und Dirac-Deltas für die Eigenschaften des zu erzeugenden bzw. vernichtenden Teilchens entsprechen, richtig?
|
Das ist recht unverständlich ausgedrückt.
Erzeuger und Vernichter erhöhen und verringern jeweils die Anzahl der Teilchen mit den entsprechenden Quantenzahlen innerhalb des Zustands, falls es das ist, was du mit "dem Eigenwert eines Zustands" meinst.
Ihre Wirkung läßt sich nicht durch Multiplikation mit Delta-Funktionen beschreiben. Wie kommst du darauf? |
|
 |
gnt
Gast
|
 gnt Verfasst am: 16. Aug 2017 11:49 Titel: gnt Verfasst am: 16. Aug 2017 11:49 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: |
Ihre Wirkung läßt sich nicht durch Multiplikation mit Delta-Funktionen beschreiben. Wie kommst du darauf? |
Wegen Formel 4.2.3 bei Weinberg:
\Phi_{q_1 q_2 ... q_N}=\sum_{r=1}^{N} (\pm)^{r+1}\delta(q-q_r)\Phi_{q_1...q_{r-1}q_{r+1}...q_N})
Wenn es das nicht ist, wie sieht dann so ein Erzeuger oder Vernichter explizit aus?
Ich hatte jetzt die Vorstellung entwickelt, dass der Fock-Raum durch jede mögliche ein-Teilchen-Wellenfunktion aufgespannt wird, und ein Erzeuger per Kronecker- und Dirac-Delta-Funktion diese Basiszustände zum Systemzustand hinzufügt. War wohl falsch.  |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 16. Aug 2017 13:13 Titel: index_razor Verfasst am: 16. Aug 2017 13:13 Titel: |
 |
|
Das ist alles noch ein bißchen verworren. Gehen wir das mal langsam an.
| gnt hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: |
Ihre Wirkung läßt sich nicht durch Multiplikation mit Delta-Funktionen beschreiben. Wie kommst du darauf? |
Wegen Formel 4.2.3 bei Weinberg:
\Phi_{q_1 q_2 ... q_N}=\sum_{r=1}^{N} (\pm)^{r+1}\delta(q-q_r)\Phi_{q_1...q_{r-1}q_{r+1}...q_N})
Wenn es das nicht ist, wie sieht dann so ein Erzeuger oder Vernichter explizit aus?
|
Diese Formel beschreibt die Wirkung des Vernichtungsoperators auf bestimmte Basiszustände des Fockraums. Schau mal genau hin: Das ist keine Multiplikation mit  . Der Teilcheninhalt des Zustands hat sich geändert. Darauf kommt es an. Rechts fehlt nun je ein Einteilchenzustand mit genau den Quantenzahlen q. . Der Teilcheninhalt des Zustands hat sich geändert. Darauf kommt es an. Rechts fehlt nun je ein Einteilchenzustand mit genau den Quantenzahlen q.
Wenn du solche allgemeinen Formeln besser verstehen willst, wende sie doch einfach auf einen Spezialfall an, z.B. einen Einteilchenzustand  , der genau die Quantenzahlen trägt, die , der genau die Quantenzahlen trägt, die ) vernichtet. Das Ergebnis ist ein Nullteilchenzustand, also das Vakuum vernichtet. Das Ergebnis ist ein Nullteilchenzustand, also das Vakuum
|q\rangle = |0\rangle.)
Wenn stattdessen der initiale Zustand von q verschiedene Quantenzahlen trägt, wird er komplett vernichtet
|q'\rangle = 0)
für  . Würdest du eine oder beide dieser Gleichungen als "Multipliktion mit der Delta-Funktion" beschreiben? . Würdest du eine oder beide dieser Gleichungen als "Multipliktion mit der Delta-Funktion" beschreiben?
| Zitat: |
Ich hatte jetzt die Vorstellung entwickelt, dass der Fock-Raum durch jede mögliche ein-Teilchen-Wellenfunktion aufgespannt wird, und ein Erzeuger per Kronecker- und Dirac-Delta-Funktion diese Basiszustände zum Systemzustand hinzufügt. War wohl falsch. ?( |
Der Fockraum wird nicht durch Ein-Teilchen-Wellenfunktionen aufgespannt, sondern durch Zustände beliebiger Teilchenzahl. Das sind symmetrisierte oder antisymmetrisierte Produkte von Ein-Teilchen-Zuständen.
Deine Beschreibung der Wirkung von 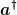 ergibt nach wie vor keinen Sinn für mich. Was soll heißen, daß ein "Basiszustand dem Systemzustand per Kronecker- und Dirac-Delta-Funktion hinzugefügt" wird? ergibt nach wie vor keinen Sinn für mich. Was soll heißen, daß ein "Basiszustand dem Systemzustand per Kronecker- und Dirac-Delta-Funktion hinzugefügt" wird? |
|
 |
gnt
Gast
|
 gnt Verfasst am: 16. Aug 2017 14:12 Titel: gnt Verfasst am: 16. Aug 2017 14:12 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | gnt hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: |
Ihre Wirkung läßt sich nicht durch Multiplikation mit Delta-Funktionen beschreiben. Wie kommst du darauf? |
Wegen Formel 4.2.3 bei Weinberg:
\Phi_{q_1 q_2 ... q_N}=\sum_{r=1}^{N} (\pm)^{r+1}\delta(q-q_r)\Phi_{q_1...q_{r-1}q_{r+1}...q_N})
Wenn es das nicht ist, wie sieht dann so ein Erzeuger oder Vernichter explizit aus?
|
Diese Formel beschreibt die Wirkung des Vernichtungsoperators auf bestimmte Basiszustände des Fockraums. Schau mal genau hin: Das ist keine Multiplikation mit  . Der Teilcheninhalt des Zustands hat sich geändert. Darauf kommt es an. Rechts fehlt nun je ein Einteilchenzustand mit genau den Quantenzahlen q. . Der Teilcheninhalt des Zustands hat sich geändert. Darauf kommt es an. Rechts fehlt nun je ein Einteilchenzustand mit genau den Quantenzahlen q. |
Das fehlende 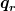 hatte ich übersehen. Man hat es demnach bei dem Phi auf der rechten Seite der Gleichung mit der Menge aller Zustände zu tun, welche um genau ein Teilchen weniger enthalten wie das Phi auf der linken Seite der Gleichung und mit dem hatte ich übersehen. Man hat es demnach bei dem Phi auf der rechten Seite der Gleichung mit der Menge aller Zustände zu tun, welche um genau ein Teilchen weniger enthalten wie das Phi auf der linken Seite der Gleichung und mit dem  wird nur der richtige selektiert. Richtig? Dann ist die Aussage der Gleichung wesentlich geringer als ich dachte, und bezieht sich eigentlich nur auf die korrekte Behandlung von Bosonen und Fermionen. wird nur der richtige selektiert. Richtig? Dann ist die Aussage der Gleichung wesentlich geringer als ich dachte, und bezieht sich eigentlich nur auf die korrekte Behandlung von Bosonen und Fermionen.
| index_razor hat Folgendes geschrieben: |
Wenn du solche allgemeinen Formeln besser verstehen willst, wende sie doch einfach auf einen Spezialfall an, z.B. einen Einteilchenzustand  , der genau die Quantenzahlen trägt, die , der genau die Quantenzahlen trägt, die ) vernichtet. Das Ergebnis ist ein Nullteilchenzustand, also das Vakuum vernichtet. Das Ergebnis ist ein Nullteilchenzustand, also das Vakuum
|q\rangle = |0\rangle.)
Wenn stattdessen der initiale Zustand von q verschiedene Quantenzahlen trägt, wird er komplett vernichtet
|q'\rangle = 0)
für  . Würdest du eine oder beide dieser Gleichungen als "Multipliktion mit der Delta-Funktion" beschreiben? . Würdest du eine oder beide dieser Gleichungen als "Multipliktion mit der Delta-Funktion" beschreiben? |
Nein. Du hast Recht!
Diese Schreibweise besagt aber leider nur was passiert, nicht wie es berechnet wird.
Kannst Du mir im Weinberg eine Formel nennen, mit der für (weil mich ja erst einmal die QED interessiert) z.B. ein Elektron und ein Photon das berechnet wird:
|0\rangle = |q\rangle.)
|q\rangle = |0\rangle.)
Also, ganz ohne Bra-Ket-Notation. Wie sieht |0>, |q>, a und 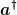 aus? aus?
| index_razor hat Folgendes geschrieben: |
Der Fockraum wird nicht durch Ein-Teilchen-Wellenfunktionen aufgespannt, sondern durch Zustände beliebiger Teilchenzahl. Das sind symmetrisierte oder antisymmetrisierte Produkte von Ein-Teilchen-Zuständen. |
Ach so. Danke!
| index_razor hat Folgendes geschrieben: |
Deine Beschreibung der Wirkung von 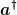 ergibt nach wie vor keinen Sinn für mich. Was soll heißen, daß ein "Basiszustand dem Systemzustand per Kronecker- und Dirac-Delta-Funktion hinzugefügt" wird? ergibt nach wie vor keinen Sinn für mich. Was soll heißen, daß ein "Basiszustand dem Systemzustand per Kronecker- und Dirac-Delta-Funktion hinzugefügt" wird? |
Das war wohl Unsinn. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 16. Aug 2017 14:48 Titel: jh8979 Verfasst am: 16. Aug 2017 14:48 Titel: |
 |
|
| gnt hat Folgendes geschrieben: |
Diese Schreibweise besagt aber leider nur was passiert, nicht wie es berechnet wird.
Kannst Du mir im Weinberg eine Formel nennen, mit der für (weil mich ja erst einmal die QED interessiert) z.B. ein Elektron und ein Photon das berechnet wird:
|0\rangle = |q\rangle.)
|q\rangle = |0\rangle.)
Also, ganz ohne Bra-Ket-Notation. Wie sieht |0>, |q>, a und 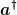 aus? aus?
|
Nein, weil da nichts berechnet wird. Das ist die Definition von a und adagger (oder Wahlweise deines Hilbertraums, je nach Sichtweise).
Zuletzt bearbeitet von jh8979 am 16. Aug 2017 16:52, insgesamt einmal bearbeitet |
|
 |
gnt
Gast
|
 gnt Verfasst am: 16. Aug 2017 16:39 Titel: gnt Verfasst am: 16. Aug 2017 16:39 Titel: |
 |
|
| jh8979 hat Folgendes geschrieben: | | Nein, weil da nichts berechnet wird. Das ist die Definition von a und adages (oder Wahlweise deines Hilbertraums, je nach Sichtweise). |
Bedeutet das, dass die Bewegungsgleichungen nicht einen Zustandsvektor, sondern den ganzen Hilbertraum verändern? |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 16. Aug 2017 16:53 Titel: jh8979 Verfasst am: 16. Aug 2017 16:53 Titel: |
 |
|
| gnt hat Folgendes geschrieben: | | jh8979 hat Folgendes geschrieben: | | Nein, weil da nichts berechnet wird. Das ist die Definition von a und adages (oder Wahlweise deines Hilbertraums, je nach Sichtweise). |
Bedeutet das, dass die Bewegungsgleichungen nicht einen Zustandsvektor, sondern den ganzen Hilbertraum verändern? |
Nein, wieso sollten sie? Der ist ja gegeben, sobald man einmal angefangen hat. |
|
 |
gnt
Gast
|
 gnt Verfasst am: 16. Aug 2017 17:36 Titel: gnt Verfasst am: 16. Aug 2017 17:36 Titel: |
 |
|
| jh8979 hat Folgendes geschrieben: | | gnt hat Folgendes geschrieben: | | jh8979 hat Folgendes geschrieben: | | Nein, weil da nichts berechnet wird. Das ist die Definition von a und adages (oder Wahlweise deines Hilbertraums, je nach Sichtweise). |
Bedeutet das, dass die Bewegungsgleichungen nicht einen Zustandsvektor, sondern den ganzen Hilbertraum verändern? |
Nein, wieso sollten sie? Der ist ja gegeben, sobald man einmal angefangen hat. |
Weil ich nicht mehr sehe, wodurch ein Zustand beschrieben ist, und wo die Zeitentwicklung ansetzen kann.
Wenn man |q> und a nicht anschreiben kann, und in der Dirac-Gleichung psi auf a beruht, dann habe ich den Eindruck, dass da irgendetwas fehlt - oder ich bin weit davon entfernt, das Konzept der QFT zu verstehen. Irgendwie muss doch die Dirac-Gleichung eine Wellenfunktion "ausspucken". Also, es muss doch irgendein Bindeglied zwischen der abstrakten Notation (die ja schön und schlüssig wirkt) und Wellenfunktionen geben.
Den abstrakten Teil in der Bra-Ket-Notation hat ja Tom im Thread https://www.physikerboard.de/topic,51797,-n-teilchensysteme.html schön beschrieben, aber wenn ich jetzt konkret Fermionen und Photonen beschreiben/berechnen will, brauche ich doch die Dirac-Gleichung, und darauf basierend Wellenfunktionen. Ich dachte, das liefe zumindest ähnlich der Behandlung der Schrödingergleichung.
Ich bin total verwirrt. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 16. Aug 2017 18:57 Titel: index_razor Verfasst am: 16. Aug 2017 18:57 Titel: |
 |
|
| gnt hat Folgendes geschrieben: |
Das fehlende 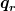 hatte ich übersehen. Man hat es demnach bei dem Phi auf der rechten Seite der Gleichung mit der Menge aller Zustände zu tun, welche um genau ein Teilchen weniger enthalten wie das Phi auf der linken Seite der Gleichung und mit dem hatte ich übersehen. Man hat es demnach bei dem Phi auf der rechten Seite der Gleichung mit der Menge aller Zustände zu tun, welche um genau ein Teilchen weniger enthalten wie das Phi auf der linken Seite der Gleichung und mit dem  wird nur der richtige selektiert. Richtig? wird nur der richtige selektiert. Richtig?
|
Diese Beschreibung kommt dem Sachverhalt schon deutlich näher finde ich.
Was eigentlich passiert ist eine Art Kontraktion des Zustands. Das bedeutet in einem Produkt aus n-Einteilchen-Zuständen bildet man das Skalarprodukt (Hilbertraumprodukt) mit einem der Faktoren und formt so ein Produkt aus n-1 Einteilchenzuständen. Im einzelnen funktioniert das so: ein n-Teilchenzustand hat die allgemeine Form eines (anti-)symmetrisierten Produkts
|\psi_{\pi(1)}\rangle \cdots |\psi_{\pi(n)}\rangle )
(Hier gilt das Minuszeichen, wenn }\rangle \cdots |\psi_{\pi(n)}\rangle) eine ungerade Anzahl von Fermionenvertauschungen gegenüber eine ungerade Anzahl von Fermionenvertauschungen gegenüber  aufweist, ansonsten gilt das Pluszeichen.) aufweist, ansonsten gilt das Pluszeichen.)
Der Operator  , der einen Zustand , der einen Zustand 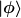 vernichtet, wirkt so vernichtet, wirkt so
^{n_r}\sum_{\mathrm{Perm.'}}(\pm) \langle\phi,\psi_{r}\rangle|\psi_{\pi(1)}\rangle\cdots\widehat{|\psi_{r}\rangle}\cdots |\psi_{\pi(n)}\rangle.)
Hierbei ist  eine Permutation der Indizes 1 bis n ausgenommen r und in eine Permutation der Indizes 1 bis n ausgenommen r und in ^{n_r}) gilt das Minuszeichen, wenn an der r-ten Stelle in gilt das Minuszeichen, wenn an der r-ten Stelle in 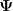 ein Fermion steht, ansonsten das Pluszeichen; Außerdem ist ein Fermion steht, ansonsten das Pluszeichen; Außerdem ist  die Anzahl der Fermionen unter den ersten r-1 Teilchen im Zustand die Anzahl der Fermionen unter den ersten r-1 Teilchen im Zustand 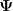 . Das . Das  bedeutet, daß dieser Term auszulassen ist. bedeutet, daß dieser Term auszulassen ist.
Die  -Funktionen kommen nur dadurch ins Spiel, daß Weinberg hier auf der "orthonormierten" Basis der Impulseigenzustände rechnet und dann gilt eben -Funktionen kommen nur dadurch ins Spiel, daß Weinberg hier auf der "orthonormierten" Basis der Impulseigenzustände rechnet und dann gilt eben
)
| Zitat: |
Dann ist die Aussage der Gleichung wesentlich geringer als ich dachte, und bezieht sich eigentlich nur auf die korrekte Behandlung von Bosonen und Fermionen.
|
Was meinst du damit? Fermionen und Bosonen sind ja auch die einzig gängigen Alternativen. Damit ist die Gleichung recht universell gültig.
Edit: Formel und Erläuterung korrigiert.
Zuletzt bearbeitet von index_razor am 16. Aug 2017 23:58, insgesamt 2-mal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 16. Aug 2017 19:09 Titel: TomS Verfasst am: 16. Aug 2017 19:09 Titel: |
 |
|
Die Erzeuger und Vernichter sind so konstruiert (oder definiert, je nach Sichtweise), dass der Feldoperator psi, den du durch die Fourier-Darstellung erhältst, die freie Dirac-Gleichung automatisch löst. Die Zeitentwicklung folgt einfach, indem du je Fourierkomponente das entsprechende


einbaust (bzw. das ist im exp[-ipx] in 4er-Notation implizit enthalten).
Das ist letztlich so wie beim harmonischen Oszillator auch: die Auf- und Absteiger lösen die Zeitentwicklung trivialerweise per Konstruktion.
Du solltest dir mal den Dirac-Hamiltonian anschauen und die Zeitentwicklung bzw. die Heisenbergsche Bewegungsgleichung sowohl für die Erzeuger und Vernichter als auch für den Feldoperator psi im Heisenbergbild durchrechnen, um das zu zeigen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 16. Aug 2017 19:24 Titel: index_razor Verfasst am: 16. Aug 2017 19:24 Titel: |
 |
|
| gnt hat Folgendes geschrieben: |
Weil ich nicht mehr sehe, wodurch ein Zustand beschrieben ist, und wo die Zeitentwicklung ansetzen kann.
|
Das ist eigentlich genau so wie in der nicht-relativistischen Quantenmechanik. Nur der Hamilton-Operator  ist in der relativistischen Feldtheorie von speziellerer Form. ist in der relativistischen Feldtheorie von speziellerer Form.
| Zitat: |
Wenn man |q> und a nicht anschreiben kann, und in der Dirac-Gleichung psi auf a beruht, dann habe ich den Eindruck, dass da irgendetwas fehlt - oder ich bin weit davon entfernt, das Konzept der QFT zu verstehen. Irgendwie muss doch die Dirac-Gleichung eine Wellenfunktion "ausspucken".
|
Die Dirac-Gleichung beschreibt die Entwicklung der fermionischen Felder, nicht der Wellenfunktion. Die Zeitentwicklung der Wellenfunktion wird wie immer durch die Schrödinger-Gleichung beschrieben
 |
|
 |
gnt
Gast
|
 gnt Verfasst am: 16. Aug 2017 21:40 Titel: gnt Verfasst am: 16. Aug 2017 21:40 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | Der Operator  , der einen Zustand , der einen Zustand 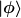 vernichtet, wirkt so vernichtet, wirkt so
 \langle\phi,\psi_{\psi(1)}\rangle|\psi_{\pi(2)}\rangle\cdots|\psi_{\pi(n)}\rangle,)
d.h. er ist linear und wirkt durch Skalarproduktbildung auf dem ersten Element des eines Produktes  . . |
Dem kann ich folgen. Danke!
| index_razor hat Folgendes geschrieben: |
| Zitat: |
Dann ist die Aussage der Gleichung wesentlich geringer als ich dachte, und bezieht sich eigentlich nur auf die korrekte Behandlung von Bosonen und Fermionen.
|
Was meinst du damit? Fermionen und Bosonen sind ja auch die einzig gängigen Alternativen. Damit ist die Gleichung recht universell gültig. |
Ich meinte damit, dass in der Gleichung die eigentliche Vernichtung nicht gezeigt wird - Du hast das mit der obigen Formel mit dem Skalarprodukt getan. |
|
 |
gnt
Gast
|
 gnt Verfasst am: 16. Aug 2017 22:29 Titel: gnt Verfasst am: 16. Aug 2017 22:29 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Die Erzeuger und Vernichter sind so konstruiert (oder definiert, je nach Sichtweise), dass der Feldoperator psi, den du durch die Fourier-Darstellung erhältst, die freie Dirac-Gleichung automatisch löst. Die Zeitentwicklung folgt einfach, indem du je Fourierkomponente das entsprechende


einbaust (bzw. das ist im exp[-ipx] in 4er-Notation implizit enthalten). |
Das ist ja eigentlich das gleiche wie in der nicht-relativistischen QM. Was ich aber noch immer nicht verstanden habe ist, wie durch die Dirac-Gleichung Zustände definiert werden.
Würde ich in der Dirac-Gleichung psi(x) als 4 normale, komplexwertige Funktionen annehmen, wäre mir das Prinzip (also, abgesehen von Mathematischen Problemen) klar - ich müsste eben diese 4 Funktionen errechnen. Aber dann wäre, wenn ich das richtig verstanden habe, nichts quantisiert.
Zur Quantisierung kommt der Feldoperator hinzu, jedoch ist es so, dass psi(x) nur a als freie Funktionen enthält. Demnach müsste a gesucht sein, aber das hat hier nur die Parameter p und sigma. In Kombination mit exp(ipx) und den Dirac-Spinoren der Koeffizientenfunktionen bliebe so wie ich das jetzt sehe für a nur, dass dieses für eben jedes p und jedes sigma eine komplexe Zahl liefert, und damit nur Amplitude und Phase bestimmt. Eingesetzt in psi(x) ergäbe das eine bzw. vier Wellenfunktionen, aber ist das alles? Ist dann der Fockraum letztlich nur definiert durch eine Funktion (a) in Abhängigkeit von p und sigma (und der Teilchenart natürlich)?
| TomS hat Folgendes geschrieben: |
Du solltest dir mal den Dirac-Hamiltonian anschauen und die Zeitentwicklung bzw. die Heisenbergsche Bewegungsgleichung sowohl für die Erzeuger und Vernichter als auch für den Feldoperator psi im Heisenbergbild durchrechnen, um das zu zeigen. |
Danke für den Rat, aber ich verstehe die Aufgabe gar nicht. Den Dirac-Hamiltonian habe ich analysiert. Die Zeitentwicklung müsste dann doch wie üblich "einfach" (d.h.: schwer  ) durch ) durch  U) gegeben sein. gegeben sein. |
|
 |
gnt
Gast
|
 gnt Verfasst am: 16. Aug 2017 22:34 Titel: gnt Verfasst am: 16. Aug 2017 22:34 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Die Dirac-Gleichung beschreibt die Entwicklung der fermionischen Felder, nicht der Wellenfunktion. |
Schreibst Du "Felder", weil meist mehr Komponenten je Feldpunkt (Vektor, Spinor etc.) vorkommen? Sollte ich psi(x), das Dirac-Spinoren beschreibt, nicht als Wellenfunktion bezeichnen? Oder verstehe ich Dich falsch? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 16. Aug 2017 23:12 Titel: TomS Verfasst am: 16. Aug 2017 23:12 Titel: |
 |
|
Ich denke, du vermisst den Schritt der "zweiten Quantisierung".
Die "erste Quantisierung" führt die Wellenfunktion psi ein, dargestellt mittels Fourierkompinenten bzw. Amplituden a und a-dagger.
Die "zweite Quantisierung" geht aus von der Lagrangedichte der Dirac-Gleichung; daraus ergeben sich die kanonisch konjugierten Größen psi und psi-dagger, sowie jetzt in der "zweiten Quantisierung" deren Interpretation als Operatoren sowie die Ersetzung der Poisson-Klammern durch Kommutatoren. Die Amplituden a und a-dagger werden nun ebenfalls so uminterpretiert, dass sie wieder Operatoren mit den gewünschten Kommutatoren entsprechen.
Soweit klar? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 17. Aug 2017 00:02 Titel: index_razor Verfasst am: 17. Aug 2017 00:02 Titel: |
 |
|
| gnt hat Folgendes geschrieben: |
Ich meinte damit, dass in der Gleichung die eigentliche Vernichtung nicht gezeigt wird - Du hast das mit der obigen Formel mit dem Skalarprodukt getan. |
Nach weiterer Überlegung ist mir aufgefallen, daß die Kombinatorik in der Formel deutlich komplizierter ist, als ich erst angenommen hatte. Deswegen habe ich sie und die Erläuterung darunter noch mal korrigiert.
Diese kombinatorischen Komplikationen sind übrigens der Grund warum Weinberg nur mit sehr sorgfältig symmetrisierten Zuständen arbeitet. Lies dir vielleicht nochmal seine Diskussion in dem entsprechenden Abschnitt genau durch. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 17. Aug 2017 00:08 Titel: index_razor Verfasst am: 17. Aug 2017 00:08 Titel: |
 |
|
| gnt hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Die Dirac-Gleichung beschreibt die Entwicklung der fermionischen Felder, nicht der Wellenfunktion. |
Schreibst Du "Felder", weil meist mehr Komponenten je Feldpunkt (Vektor, Spinor etc.) vorkommen? Sollte ich psi(x), das Dirac-Spinoren beschreibt, nicht als Wellenfunktion bezeichnen? Oder verstehe ich Dich falsch? |
Mein Punkt ist, daß das 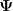 in der Dirac-Gleichung keine Wellenfunktion beschreibt, sondern ein Quantenfeld, also letztendlich einen Operator auf dem Hilbertraum. Dies sollte man nicht mit den Zuständen, also den Vektoren in der Dirac-Gleichung keine Wellenfunktion beschreibt, sondern ein Quantenfeld, also letztendlich einen Operator auf dem Hilbertraum. Dies sollte man nicht mit den Zuständen, also den Vektoren 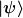 etc. aus dem Hilbertraum verwechseln. Letztere, bzw. deren Darstellung bzgl. einer Basis etc. aus dem Hilbertraum verwechseln. Letztere, bzw. deren Darstellung bzgl. einer Basis =\langle x,\psi\rangle) , sind es, die man normalerweise als "Wellenfunktion" bezeichnet. , sind es, die man normalerweise als "Wellenfunktion" bezeichnet. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 17. Aug 2017 00:18 Titel: jh8979 Verfasst am: 17. Aug 2017 00:18 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: |
Diese kombinatorischen Komplikationen sind übrigens der Grund warum Weinberg nur mit sehr sorgfältig symmetrisierten Zuständen arbeitet. Lies dir vielleicht nochmal seine Diskussion in dem entsprechenden Abschnitt genau durch. |
Das ist übrigens immer ein sehr guter Tipp: Ich habe schon oft nach stundenlangen fachlichen Diskussionen festgestellt, dass es klar und deutlich in einem Satz im Weinberg steht ... man es nur nicht richtig gelesen hat 
(Das ist einer der Gründe, die es Anfängern schwer machen im Weinberg... er ist einfach zu gut  ) ) |
|
 |
gnt
Gast
|
 gnt Verfasst am: 17. Aug 2017 13:48 Titel: gnt Verfasst am: 17. Aug 2017 13:48 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Ich denke, du vermisst den Schritt der "zweiten Quantisierung".
Die "erste Quantisierung" führt die Wellenfunktion psi ein, dargestellt mittels Fourierkompinenten bzw. Amplituden a und a-dagger.
Die "zweite Quantisierung" geht aus von der Lagrangedichte der Dirac-Gleichung; daraus ergeben sich die kanonisch konjugierten Größen psi und psi-dagger, sowie jetzt in der "zweiten Quantisierung" deren Interpretation als Operatoren sowie die Ersetzung der Poisson-Klammern durch Kommutatoren. Die Amplituden a und a-dagger werden nun ebenfalls so uminterpretiert, dass sie wieder Operatoren mit den gewünschten Kommutatoren entsprechen.
Soweit klar? |
Leider nicht.
Für das reelle Skalarfeld habe ich hier einmal eine für mich fast schon verständliche Erklärung gefunden: https://en.wikipedia.org/wiki/Canonical_quantization#Real_scalar_field
Dort wird die Quantisierung auf zweierlei Art gemacht:
1. Der Kommutator von phi(x) und pi(y) wird gleich ) gesetzt. gesetzt.
2. H wird nur aus phi und pi mit ganzzahligem k rekonstruiert. (Wobei mir nicht klar ist, wo das omega dort herkommt.)
In diesem H stehen nur die Fourier-Transformierten der Felder, und das wird dann für die Operatoren 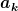 und und  umgeschrieben (warum die in phi und pi gemischten Terme wegfallen ist mir aber auch nicht klar.). umgeschrieben (warum die in phi und pi gemischten Terme wegfallen ist mir aber auch nicht klar.).
Am Ende steht dann für H das, was Du in dem anderen Thread geschrieben hast.
Jedenfalls erscheint es mir so, dass durch die explizit angeschriebene Form von 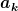 und und  , in denen nur phi(x) und pi(x) unbekannt sind, H wieder etwas greifbarer in dem Sinne wird, wie man es in der Schrödingergleichung hat. Trotzdem: Dort hat man diese zwei Funktionen, in Weinbergs Formel für psi(x) sieht das ganz anders aus, und wenn ich das oben richtig verstanden habe, kann man a und adagger in dem Fall nicht explizit angeben. , in denen nur phi(x) und pi(x) unbekannt sind, H wieder etwas greifbarer in dem Sinne wird, wie man es in der Schrödingergleichung hat. Trotzdem: Dort hat man diese zwei Funktionen, in Weinbergs Formel für psi(x) sieht das ganz anders aus, und wenn ich das oben richtig verstanden habe, kann man a und adagger in dem Fall nicht explizit angeben.
Ist denn dieses
=(2\pi)^{-3/2}\sum_\sigma \int d^3 p [u_l(p,\sigma)e^{ipx}a(p,\sigma)+v_l(p,\sigma)e^{-ipx}a^{c \dagger}(p,\sigma)])
nicht in die Dirac-Gleichung einzusetzen? |
|
 |
gnt
Gast
|
 gnt Verfasst am: 17. Aug 2017 13:59 Titel: gnt Verfasst am: 17. Aug 2017 13:59 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | gnt hat Folgendes geschrieben: |
Ich meinte damit, dass in der Gleichung die eigentliche Vernichtung nicht gezeigt wird - Du hast das mit der obigen Formel mit dem Skalarprodukt getan. |
Nach weiterer Überlegung ist mir aufgefallen, daß die Kombinatorik in der Formel deutlich komplizierter ist, als ich erst angenommen hatte. Deswegen habe ich sie und die Erläuterung darunter noch mal korrigiert. |
Danke!
Die Orthonormierung sollte ja gerade ausschlaggebend sein, dass das mit dem Skalarprodukt funktioniert.
| index_razor hat Folgendes geschrieben: | Mein Punkt ist, daß das 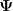 in der Dirac-Gleichung keine Wellenfunktion beschreibt, sondern ein Quantenfeld, also letztendlich einen Operator auf dem Hilbertraum. Dies sollte man nicht mit den Zuständen, also den Vektoren in der Dirac-Gleichung keine Wellenfunktion beschreibt, sondern ein Quantenfeld, also letztendlich einen Operator auf dem Hilbertraum. Dies sollte man nicht mit den Zuständen, also den Vektoren 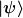 etc. aus dem Hilbertraum verwechseln. Letztere, bzw. deren Darstellung bzgl. einer Basis etc. aus dem Hilbertraum verwechseln. Letztere, bzw. deren Darstellung bzgl. einer Basis =\langle x,\psi\rangle) , sind es, die man normalerweise als "Wellenfunktion" bezeichnet. , sind es, die man normalerweise als "Wellenfunktion" bezeichnet. |
Ja, das verstehe ich. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 17. Aug 2017 14:57 Titel: index_razor Verfasst am: 17. Aug 2017 14:57 Titel: |
 |
|
| gnt hat Folgendes geschrieben: |
Ist denn dieses
=(2\pi)^{-3/2}\sum_\sigma \int d^3 p [u_l(p,\sigma)e^{ipx}a(p,\sigma)+v_l(p,\sigma)e^{-ipx}a^{c \dagger}(p,\sigma)])
nicht in die Dirac-Gleichung einzusetzen? |
Jedes
 = \sum_\sigma \int \dd^3 p\left( f_{\ell,\sigma}(x,p)a_{p,\sigma} + g_{\ell,\sigma}(x,p)a^{c\dagger}_{p,\sigma}\right))
erfüllt doch die Dirac-Gleichung, wenn
f_{\ell,\sigma}(x,p)=0)
und
g_{\ell,\sigma}(x,p)=0)
Das hat doch mit der Definition von  und und 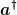 nicht viel zu tun. nicht viel zu tun.
Mir ist nicht klar, wie du darauf kommst  und und 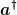 seien nicht "explizit angebbar". Sowohl Erzeuger und Vernichter als auch die Feldoperatoren sind lediglich durch ihre Wirkung auf den Fockraum definiert. Ob du nun die Felder, wie im Weinberg, durch Erzeuger und Vernichter oder umgekehrt ausdrückst, ändert doch an der Situation nichts. seien nicht "explizit angebbar". Sowohl Erzeuger und Vernichter als auch die Feldoperatoren sind lediglich durch ihre Wirkung auf den Fockraum definiert. Ob du nun die Felder, wie im Weinberg, durch Erzeuger und Vernichter oder umgekehrt ausdrückst, ändert doch an der Situation nichts. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 17. Aug 2017 15:31 Titel: index_razor Verfasst am: 17. Aug 2017 15:31 Titel: |
 |
|
Übrigens, kanonische Quantisierung, Lagrange-Formalismus, Feldgleichungen etc. haben m.E. allesamt wenig mit dem zu tun, was du hier nicht verstehst. Sie haben außerdem wenig mit dem Ansatz von Weinberg zu tun (obwohl er sie typischerweise natürlich ebenfalls diskutiert, aber erst weiter hinten im Text).
Deswegen glaube ich eigentlich auch nicht, daß sie uns hier weiterhelfen. |
|
 |
gnt
Gast
|
 gnt Verfasst am: 17. Aug 2017 16:03 Titel: gnt Verfasst am: 17. Aug 2017 16:03 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: |
Mir ist nicht klar, wie du darauf kommst  und und 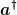 seien nicht "explizit angebbar". seien nicht "explizit angebbar". |
Es geht mir in diesem Thread ja auch im besonderen darum, wie das für das Dirac-Feld und für das Photonfeld genau aussieht. Ich dachte ja, dass man das angeben kann, und eine Form wie  e^{-ikx}) haben sollte, aber dann hat jh8979 im Beitrag vom 16. Aug 2017 14:48 geantwortet: "Nein, weil da nichts berechnet wird.". Diese Antwort habe ich dann offenbar falsch verstanden. haben sollte, aber dann hat jh8979 im Beitrag vom 16. Aug 2017 14:48 geantwortet: "Nein, weil da nichts berechnet wird.". Diese Antwort habe ich dann offenbar falsch verstanden.
| index_razor hat Folgendes geschrieben: | | Sowohl Erzeuger und Vernichter als auch die Feldoperatoren sind lediglich durch ihre Wirkung auf den Fockraum definiert. Ob du nun die Felder, wie im Weinberg, durch Erzeuger und Vernichter oder umgekehrt ausdrückst, ändert doch an der Situation nichts. |
Tut mir leid, dass ich so langsam begreife.
Wäre demnach die Form von a nur das psi(x) nach a umgestellt?
psi(x) sollte ja eine allgemeine Lösung der Dirac-Gleichung sein, aber wie sieht eine spezielle aus? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 17. Aug 2017 16:51 Titel: index_razor Verfasst am: 17. Aug 2017 16:51 Titel: |
 |
|
| gnt hat Folgendes geschrieben: |
Es geht mir in diesem Thread ja auch im besonderen darum, wie das für das Dirac-Feld und für das Photonfeld genau aussieht. Ich dachte ja, dass man das angeben kann, und eine Form wie  e^{-ikx}) haben sollte, aber dann hat jh8979 im Beitrag vom 16. Aug 2017 14:48 geantwortet: "Nein, weil da nichts berechnet wird.". Diese Antwort habe ich dann offenbar falsch verstanden. haben sollte, aber dann hat jh8979 im Beitrag vom 16. Aug 2017 14:48 geantwortet: "Nein, weil da nichts berechnet wird.". Diese Antwort habe ich dann offenbar falsch verstanden.
|
Ist dir denn klar, wie ein Ein-Elektronen-Zustand aussieht; oder ein Mehr-Elektronenzustand? Wenn nicht, ist das anscheinend dein Grundproblem.
Wenn doch, dann mußt du eigentlich nur noch begreifen, daß zu jedem beliebigen Einteilchen-Zustand  ein Operator ein Operator  gehört, der irgendeinen n-Teilchenzustand gehört, der irgendeinen n-Teilchenzustand

auf den (n+1)-Teilchen-Zustand

abbildet (Antisymmetrisierung jeweils inbegriffen.) Das ist wohldefiniert für jeden beliebigen Zustand (zumindest zur Zufriedenheit der Physiker), egal welche Repräsentation du dir für Zustände, den Hilbertraum und seine Operatoren ausdenkst. Wenn du den Zustand z.B. über eine Impulswellenfunktion ) definierst, dann wäre in der Ortsdarstellung definierst, dann wäre in der Ortsdarstellung
}|\psi_1,\cdots,\psi_n\rangle = \frac{1}{\sqrt{2\pi}^3}\int \dd p^3 e^{ipx}\psi_\sigma(p)\psi_{1,\sigma_1}(x_1)\cdots\psi_{n,\sigma_n}(x_n) \\+ \text{vollst. Antisymmetrisierung})
Das ist aber nicht irgendwie "expliziter". Das ist nur kompliziert.
| Zitat: |
Tut mir leid, dass ich so langsam begreife.
Wäre demnach die Form von a nur das psi(x) nach a umgestellt?
|
Du brauchst dich für nichts zu entschuldigen. Von welcher Form sprichst du denn jetzt?
| Zitat: |
psi(x) sollte ja eine allgemeine Lösung der Dirac-Gleichung sein, aber wie sieht eine spezielle aus? |
Eine spezielle Lösung der freien Dirac-Gleichung sieht so aus
=(2\pi)^{-3/2}\sum_\sigma \int \dd^3 p \left(u(p,\sigma)e^{ipx}a_{p,\sigma}+v(p,\sigma)e^{-ipx}a^{c \dagger}_{p,\sigma}\right))
wobei jeweils 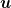 und und  die Gleichung die Gleichung
 u(p,\sigma) = 0 )
und
 v(p,\sigma) = 0 )
erfüllen. Natürlich gibt es noch weit speziellere Lösungen, z.B.  \equiv 0) . Insofern ist schon wichtig zu wissen, worauf deine Frage abzielt. . Insofern ist schon wichtig zu wissen, worauf deine Frage abzielt.
Zuletzt bearbeitet von index_razor am 21. Nov 2018 10:51, insgesamt einmal bearbeitet |
|
 |
gnt
Gast
|
 gnt Verfasst am: 17. Aug 2017 17:30 Titel: gnt Verfasst am: 17. Aug 2017 17:30 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Ist dir denn klar, wie ein Ein-Elektronen-Zustand aussieht; oder ein Mehr-Elektronenzustand? Wenn nicht, ist das anscheinend dein Grundproblem. |
Nachdem Du das fragst, liege ich wohl falsch: Meine Vermutung geht in Richtung einer Wellenfunktion, wie man sie aus der nicht-relativistischen QM kennt, also psi(x, t) (d.h. wie z.B. exp(i(kx-wt)) ), oder bei mehreren Teilchen psi(x1..xn, t) oder eben je nach Darstellung ein dazu analoger Ausdruck. Dass es ganz genau so ist, glaube ich aber allein schon wegen der zum Teil 4 Komponenten nicht - deshalb ja auch meine Frage nach dem Ergebnis von |0>) . .
| index_razor hat Folgendes geschrieben: | | Von welcher Form sprichst du denn jetzt? |
Hiervon:
=(2\pi)^{-3/2}\sum_\sigma \int d^3 p [u_l(p,\sigma)e^{ipx}a(p,\sigma)+v_l(p,\sigma)e^{-ipx}a^{c \dagger}(p,\sigma)])
Das  lässt sich durch lässt sich durch  ersetzen, und dann alles nach ersetzen, und dann alles nach  auflösen. auflösen.
| index_razor hat Folgendes geschrieben: |
Eine spezielle Lösung der freien Dirac-Gleichung sieht so aus
=(2\pi)^{-3/2}\sum_\sigma \int \dd^3 p \left(u(p,\sigma)e^{ipx}a_{p,\sigma}+v(p,\sigma)e^{-ipx}a^{c \dagger}_{p,\sigma}\right)) |
Ich drehe mich vermutlich im Kreis, aber mir ist nicht klar, was  hier ist. Eine Zahl sicher nicht, weil dann hier ist. Eine Zahl sicher nicht, weil dann  keinen Sinn ergäbe. Eine 4x4 Matrix wohl eher auch nicht, weil das mit dem Skalarprodukt dann nicht funktionieren würde. Hat keinen Sinn ergäbe. Eine 4x4 Matrix wohl eher auch nicht, weil das mit dem Skalarprodukt dann nicht funktionieren würde. Hat  noch hier unterdrückte Parameter wie x oder t? noch hier unterdrückte Parameter wie x oder t? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 17. Aug 2017 19:02 Titel: TomS Verfasst am: 17. Aug 2017 19:02 Titel: |
 |
|
Ich weiß nicht, ob es viel bringt, auf lange Formeln zu starren. Man muss die Idee - zunächst ohne Mathematik - Schritt für Schritt verstehen. Wenn ich das jetzt aber nach meiner Vorgehensweise zusammenfasse, passt dies sicher nicht zu Weinberg.
Willst du mit dem Buch weitermachen? Oder eher Neustart?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
gnt
Gast
|
 gnt Verfasst am: 17. Aug 2017 19:20 Titel: gnt Verfasst am: 17. Aug 2017 19:20 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Willst du mit dem Buch weitermachen? Oder eher Neustart? |
Das ist mir eigentlich egal - ich hänge nicht am Weinberg. Gerne würde ich auch erst einmal das Konzept ohne Formeln verstehen, aber am Ende möchte ich natürlich die mathematische Struktur im wesentlichen überblicken, oder den Weg dahin kennen, dass ich mir das dann erlesen kann. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 17. Aug 2017 19:44 Titel: jh8979 Verfasst am: 17. Aug 2017 19:44 Titel: |
 |
|
| gnt hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Willst du mit dem Buch weitermachen? Oder eher Neustart? |
Das ist mir eigentlich egal - ich hänge nicht am Weinberg. Gerne würde ich auch erst einmal das Konzept ohne Formeln verstehen, aber am Ende möchte ich natürlich die mathematische Struktur im wesentlichen überblicken, oder den Weg dahin kennen, dass ich mir das dann erlesen kann. |
Ich würde (wie schon erwähnt) einen anderen Weg vorschlagen:
Zuerst das Rechnen mit einer QFT lernen. Dafür ist der Peskin (gerade zum Selberlernen) super. Dann hast Du eine (grobe) Ahnung worum es eigentlich geht... dann kann mein weiter an den Konzepten feilen.
Und für diese Konzepte: Weinberg!!!!!! ... aber am Anfang wird das zu schwer für Dich sein. Es gibt leider noch kein "How to Read Weinberg's QFT Books"-Guide ... Hätte gern mal Zeit den zu Schreiben.. es würde sich echt lohnen bei den Büchern... aber ohne den ist man als Anfänger ziemlich verloren.
PS: @TomS
| TomS hat Folgendes geschrieben: | Wenn ich das jetzt aber nach meiner Vorgehensweise zusammenfasse, passt dies sicher nicht zu Weinberg.
|
Dann solltest Du Deine Vorgehensweise ändern 
(Konnte ich mir jetzt nicht verkneifen  ) ) |
|
 |
gnt
Gast
|
 gnt Verfasst am: 17. Aug 2017 19:56 Titel: gnt Verfasst am: 17. Aug 2017 19:56 Titel: |
 |
|
| jh8979 hat Folgendes geschrieben: | | gnt hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Willst du mit dem Buch weitermachen? Oder eher Neustart? |
Das ist mir eigentlich egal - ich hänge nicht am Weinberg. Gerne würde ich auch erst einmal das Konzept ohne Formeln verstehen, aber am Ende möchte ich natürlich die mathematische Struktur im wesentlichen überblicken, oder den Weg dahin kennen, dass ich mir das dann erlesen kann. |
Ich würde (wie schon erwähnt) einen anderen Weg vorschlagen:
Zuerst das Rechnen mit einer QFT lernen. Dafür ist der Peskin (gerade zum Selberlernen) super. Dann hast Du eine (grobe) Ahnung worum es eigentlich geht... dann kann mein weiter an den Konzepten feilen. |
Ich kann das natürlich nicht beurteilen.
Aber ich habe mit Tom nur beste Erfahrungen gemacht. 
| jh8979 hat Folgendes geschrieben: | | Und für diese Konzepte: Weinberg!!!!!! ... aber am Anfang wird das zu schwer für Dich sein. Es gibt leider noch kein "How to Read Weinberg's QFT Books"-Guide ... Hätte gern mal Zeit den zu Schreiben.. es würde sich echt lohnen bei den Büchern... aber ohne den ist man als Anfänger ziemlich verloren. |
Das sollte ich erwähnen: Ich bin nicht nur Anfänger, sondern auch nur Hobbyist, bin also nicht einmal angehender Physiker. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 17. Aug 2017 20:03 Titel: jh8979 Verfasst am: 17. Aug 2017 20:03 Titel: |
 |
|
| gnt hat Folgendes geschrieben: |
Aber ich habe mit Tom nur beste Erfahrungen gemacht. 
|
Kann mich auch nicht beklagen  
| Zitat: |
| jh8979 hat Folgendes geschrieben: | | Und für diese Konzepte: Weinberg!!!!!! ... aber am Anfang wird das zu schwer für Dich sein. Es gibt leider noch kein "How to Read Weinberg's QFT Books"-Guide ... Hätte gern mal Zeit den zu Schreiben.. es würde sich echt lohnen bei den Büchern... aber ohne den ist man als Anfänger ziemlich verloren. |
Das sollte ich erwähnen: Ich bin nicht nur Anfänger, sondern auch nur Hobbyist, bin also nicht einmal angehender Physiker. |
Gerade dann würde ich vom Weinberg abraten. Er ist wirklich sehr gut, aber halt auch ziemlich schwer. Peskin&Schröder sind einfacher und bisschen mehr Physiker-like-passt-schon und zeigen einem wie man zu den Rechnungen kommt. Glaube das würde Dir mehr helfen. P&S sind zwar etwas schlampig manchmal, aber nur wenn sie wissen, dass sie es sein können ohne Fehler zu machen (Du wirst das beim ersten Lesen gar nicht merken). |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 17. Aug 2017 21:20 Titel: index_razor Verfasst am: 17. Aug 2017 21:20 Titel: |
 |
|
| gnt hat Folgendes geschrieben: |
Nachdem Du das fragst, liege ich wohl falsch: Meine Vermutung geht in Richtung einer Wellenfunktion, wie man sie aus der nicht-relativistischen QM kennt, also psi(x, t) (d.h. wie z.B. exp(i(kx-wt)) ), oder bei mehreren Teilchen psi(x1..xn, t) oder eben je nach Darstellung ein dazu analoger Ausdruck.
|
Ja, das stimmt auch im Prinzip. (Bei mehreren Elektronen ist noch wichtig, daß der Gesamtzustand antisymmetrisch unter Vertauschung der Einteilchenzustände ist.) Und worin besteht jetzt das Problem, sich einen Operator vorzustellen, der genau einen solchen Einteilchenzustand einem gegebenen Mehrteilchenzustand hinzufügt?
| Zitat: |
Dass es ganz genau so ist, glaube ich aber allein schon wegen der zum Teil 4 Komponenten nicht
|
Welche 4 Komponenten? Du bringst immer noch die Wellenfunktion mit dem Feld durcheinander. Unglücklicherweise werden beide oft mit dem Buchstaben 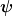 bezeichnet. bezeichnet.
| Zitat: |
- deshalb ja auch meine Frage nach dem Ergebnis von |0>) . .
|
Das ergibt einen Einteilchenzustand beschrieben durch "q", was auch immer q ist. Einen solchen Zustand bezeichnet man dann oft als  oder oder  etc. Aber ohne, daß du verrätst, was "q" sein soll, kann man da nichts konkreteres drüber sagen. etc. Aber ohne, daß du verrätst, was "q" sein soll, kann man da nichts konkreteres drüber sagen.
| Zitat: |
| index_razor hat Folgendes geschrieben: |
Eine spezielle Lösung der freien Dirac-Gleichung sieht so aus
=(2\pi)^{-3/2}\sum_\sigma \int \dd^3 p \left(u(p,\sigma)e^{ipx}a_{p,\sigma}+v(p,\sigma)e^{-ipx}a^{c \dagger}_{p,\sigma}\right)) |
Ich drehe mich vermutlich im Kreis, aber mir ist nicht klar, was  hier ist. Eine Zahl sicher nicht, weil dann hier ist. Eine Zahl sicher nicht, weil dann  keinen Sinn ergäbe. keinen Sinn ergäbe.
|
Es sind zwei verschiedene Operatoren.  vernichtet ein Teilchen mit Impuls vernichtet ein Teilchen mit Impuls 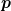 und Spin und Spin 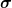 (und eventuell weiteren Quantenzahlen, die nicht explizit mit angeschrieben sind) und (und eventuell weiteren Quantenzahlen, die nicht explizit mit angeschrieben sind) und  erzeugt ein entsprechendes Anti-Teilchen mit demselben Impuls und Spin. Welche Probleme du mit diesen beiden Operatoren hast, ist mir leider nach wie vor absolut schleierhaft. Es hat wohl gar nichts mit Elektronen, Photonen oder Quantenfeldtheorie zu tun. Die Verständnisprobleme scheinen irgendwie fundamentalerer Natur zu sein. erzeugt ein entsprechendes Anti-Teilchen mit demselben Impuls und Spin. Welche Probleme du mit diesen beiden Operatoren hast, ist mir leider nach wie vor absolut schleierhaft. Es hat wohl gar nichts mit Elektronen, Photonen oder Quantenfeldtheorie zu tun. Die Verständnisprobleme scheinen irgendwie fundamentalerer Natur zu sein.
| Zitat: |
Eine 4x4 Matrix wohl eher auch nicht, weil das mit dem Skalarprodukt dann nicht funktionieren würde. Hat  noch hier unterdrückte Parameter wie x oder t? noch hier unterdrückte Parameter wie x oder t? |
Nein, x und t kommen nicht vor. Nur von den Quantenzahlen, die den zu erzeugenden/vernichtenden Zustand vollständig charakterisieren--in diesem Fall Impuls und Spin-- , hängen diese Operatoren ab. |
|
 |
gnt
Gast
|
 gnt Verfasst am: 17. Aug 2017 22:30 Titel: gnt Verfasst am: 17. Aug 2017 22:30 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Und worin besteht jetzt das Problem, sich einen Operator vorzustellen, der genau einen solchen Einteilchenzustand einem gegebenen Mehrteilchenzustand hinzufügt? |
Dann würde der Operator doch im wesentlichen aus einer Multiplikation mit einem Zustand bestehen. Es müsste etwas derartiges gelten:


Die hier stehenden psi sind aber etwas anderes als das psi (=die Lösung) der Dirac-Gleichung.
| index_razor hat Folgendes geschrieben: |
| Zitat: |
Dass es ganz genau so ist, glaube ich aber allein schon wegen der zum Teil 4 Komponenten nicht
|
Welche 4 Komponenten? Du bringst immer noch die Wellenfunktion mit dem Feld durcheinander. Unglücklicherweise werden beide oft mit dem Buchstaben 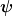 bezeichnet. bezeichnet. |
Es kann sein, dass ich mit den Begriffen Probleme habe. Warum sollte ich bei einem Dirac-Spinor
=\{\psi_1,\psi_2,\psi_3,\psi_4\}
<br />
)
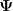 nicht, aber nicht, aber 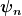 schon als Wellenfunktion bezeichnen? schon als Wellenfunktion bezeichnen? 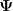 ist doch auch nur eine Wellenfunktion mit 4 (gekoppelten) Komponenten. Oder verstehe ich Dich falsch? ist doch auch nur eine Wellenfunktion mit 4 (gekoppelten) Komponenten. Oder verstehe ich Dich falsch?
| index_razor hat Folgendes geschrieben: |
| Zitat: |
- deshalb ja auch meine Frage nach dem Ergebnis von |0>) . .
|
Das ergibt einen Einteilchenzustand beschrieben durch "q", was auch immer q ist. Einen solchen Zustand bezeichnet man dann oft als  oder oder  etc. Aber ohne, daß du verrätst, was "q" sein soll, kann man da nichts konkreteres drüber sagen. etc. Aber ohne, daß du verrätst, was "q" sein soll, kann man da nichts konkreteres drüber sagen. |
Weinberg fasst mit q die Teilchenart, den Impuls und den Spin zusammen. Ich hätte auch schreiben können:
|0>)
Aber damit sage ich doch eigentlich auch nur, welche Variablen in einer bestimmten Formel welchen Wert bekommen sollen.
| index_razor hat Folgendes geschrieben: |
Nein, x und t kommen nicht vor. Nur von den Quantenzahlen, die den zu erzeugenden/vernichtenden Zustand vollständig charakterisieren--in diesem Fall Impuls und Spin-- , hängen diese Operatoren ab. |
Gut, Danke! |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 17. Aug 2017 23:11 Titel: index_razor Verfasst am: 17. Aug 2017 23:11 Titel: |
 |
|
| gnt hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Und worin besteht jetzt das Problem, sich einen Operator vorzustellen, der genau einen solchen Einteilchenzustand einem gegebenen Mehrteilchenzustand hinzufügt? |
Dann würde der Operator doch im wesentlichen aus einer Multiplikation mit einem Zustand bestehen.
|
Ja, für den Erzeuger stimmt das ja auch im Prinzip. Es ist eine Art tensorielle Multiplikation gefolgt von der Anti-Symmetrisierung aller Faktoren. Der Vernichter kontrahiert dann diesen Zustand wieder durch skalare Multiplikation. Weiter oben hast du behauptet, das wäre die klar. Aber jetzt schreibst du wieder sowas:
| Zitat: |
Es müsste etwas derartiges gelten:


|
Wie kommst du auf die Form für  ? Das widerspricht doch klar der Formel, die du gestern noch aus dem Weinberg zitiert hast. ? Das widerspricht doch klar der Formel, die du gestern noch aus dem Weinberg zitiert hast.
| Zitat: |
Die hier stehenden psi sind aber etwas anderes als das psi (=die Lösung) der Dirac-Gleichung.
|
Ja, ganz genau. Die hier vorkommenden psi beschreiben Vektoren im Hilbertraum, also Zustände. Die Lösungen der Dirac-Gleichung sind in der QFT Operatoren auf dem Hilbertraum. Diese Operatoren vernichten bestimmte Einteilchen-Zustände und erzeugen zugehörige Antiteilchen-Zustände. Aus diesem Grund spielen sie bei der Beschreibung von Prozessen mit Teilchenaustausch eine Rolle.
| Zitat: |
Es kann sein, dass ich mit den Begriffen Probleme habe. Warum sollte ich bei einem Dirac-Spinor
=\{\psi_1,\psi_2,\psi_3,\psi_4\}
<br />
)
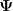 nicht, aber nicht, aber 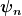 schon als Wellenfunktion bezeichnen? schon als Wellenfunktion bezeichnen?
|
Ich würde weder das eine noch das andere als "Wellenfunktion" bezeichnen. Mit "Wellenfunktion" bezeichnet man normalerweise eine bestimmte Darstellung -- meist die Ortsdarstellung -- eines Zustands, d.h. z.B.  = \langle x|\psi\rangle) . Das hat nichts mit den Feldkomponenten . Das hat nichts mit den Feldkomponenten  zu tun. zu tun.
| Zitat: |
Weinberg fasst mit q die Teilchenart, den Impuls und den Spin zusammen. Ich hätte auch schreiben können:
|0>)
Aber damit sage ich doch eigentlich auch nur, welche Variablen in einer bestimmten Formel welchen Wert bekommen sollen.
|
Solange diese Variablen den zu erzeugenden Zustand vollständig beschreiben, wüßte ich nicht, was dir ein "Erzeugungsoperator" sonst noch sagen sollte. Wenn es darum geht die angeblich fehlende Information zu beschreiben, bist du immer recht unkonkret.
Übrigens, was soll das "v={0,0, 1/2}" hier eigentlich bedeuten? |
|
 |
|
|

















 ) durch
) durch 
 )
)
