| Autor |
Nachricht |
Bubor
Anmeldungsdatum: 24.09.2016
Beiträge: 39
|
 Bubor Verfasst am: 22. Jul 2017 20:07 Titel: Wirkung von Operatoren Bubor Verfasst am: 22. Jul 2017 20:07 Titel: Wirkung von Operatoren |
 |
|
Meine Frage:
Hallo Liebe Leute 
Ich habe folgende Aufgabe: gegeben ist ein Hamiltonoperator im 6-Dimensionalem Hilbertraum mit
 + 2 \gamma B^{+} B ) mit mit
 und und  und und  . .
Ich soll nun die Eigenwerte  und und  bestimmen bestimmen
Meine Ideen:
Also ich kenn ja die Schrödingergleichung:

Ich weiß jetzt nicht wie 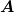 und und 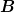 genau wirken aber ich würde einmal denken, wie folgt: genau wirken aber ich würde einmal denken, wie folgt:

Ist das so richtig?
Demnach wäre doch theoretisch meine Gleichung:
 + 2 b_{n}^{+} b_{n} \gamma \left| \Psi \right> )
Stimmt das so??
Wie könnte ich dann aber theoretisch die Eigenwerte explizit bestimmen?
Ich hoffe auf eure Hilfe und bedanke mich schoneinmal dafür 
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 22. Jul 2017 22:48 Titel: index_razor Verfasst am: 22. Jul 2017 22:48 Titel: |
 |
|
Ich denke nicht, daß die Aufgabe vollständig und korrekt wiedergegeben ist. Keine der Angaben scheint die triviale Lösung  (und damit übrigens (und damit übrigens  ) auszuschließen. ) auszuschließen.
|
|
 |
Bubor
Anmeldungsdatum: 24.09.2016
Beiträge: 39
|
 Bubor Verfasst am: 23. Jul 2017 15:52 Titel: Bubor Verfasst am: 23. Jul 2017 15:52 Titel: |
 |
|
Tut mir leid, ich habe übersehen das gelten muss:
 und nicht und nicht 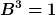
Aber mehr war wirklich nicht gegeben. Das Löst aber jetzt auch weniger das Problem.
Es ist eine Klausur Aufgabe. Demnach haben es Menschen geschrieben die auch fehler machen können. Aber wie sieht die Lösung aus, wenn wir die Triviale Lösung herausnehmen.?
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 23. Jul 2017 16:46 Titel: index_razor Verfasst am: 23. Jul 2017 16:46 Titel: |
 |
|
| Bubor hat Folgendes geschrieben: | Tut mir leid, ich habe übersehen das gelten muss:
 und nicht und nicht 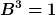
Aber mehr war wirklich nicht gegeben. Das Löst aber jetzt auch weniger das Problem.
Es ist eine Klausur Aufgabe. Demnach haben es Menschen geschrieben die auch fehler machen können. Aber wie sieht die Lösung aus, wenn wir die Triviale Lösung herausnehmen.? |
Selbst dann gibt es noch mehrere Möglichkeiten, z.B.

oder

Es fällt mir doch schwer zu glauben, daß das die gesamte Aufgabe sein soll. Der gegebene Hamiltonoperator hat gar nichts mit der Frage zu tun. Sind irgendwelche Ergebnisse aus vorigen Aufgaben stillschweigend vorausgesetzt, z.B. das Spektrum von H? Ansonsten ergibt das alles irgendwie wenig Sinn für mich.
|
|
 |
Bubor
Anmeldungsdatum: 24.09.2016
Beiträge: 39
|
 Bubor Verfasst am: 23. Jul 2017 18:10 Titel: Bubor Verfasst am: 23. Jul 2017 18:10 Titel: |
 |
|
Ich lade einfach mal die gesamte Aufgabenstellung hoch.
Die anderen beiden Aufgaben beziehen sich nur auf beweisen von Kommutatorrelation, nichts schweres. Und die andere ist auch nur mit einem gegeben Zustand eines Wasserstoff Elektrons rechnen. Auch nichts schweres. Alle Aufgaben sind auch unabhängig voneinander.
| Beschreibung: |
| Das ist einmal die gesamte Aufgabenstellung |
|

Download |
| Dateiname: |
Unbenannt.png |
| Dateigröße: |
58.32 KB |
| Heruntergeladen: |
217 mal |
|
|
 |
APWBDumbledore
Gast
|
 APWBDumbledore Verfasst am: 23. Jul 2017 18:50 Titel: APWBDumbledore Verfasst am: 23. Jul 2017 18:50 Titel: |
 |
|
Unvollständiger kann man eine Aufgabe kaum stellen...
Erstmal folgt aus den Angaben überhaupt nicht, dass A und B überhaupt unitär diagonalisierbar sind. Sagen wir mal, sie sind unitär diagonalisierbar, das ist äquivalent dazu, dass sie normal sind. Dann ist klar, dass A und B unitär sind, denn die Bedingungen A³=B³=1 setzen voraus, dass die Eigenwerte von der Form  sind, insbesondere auf dem Einheitskreis liegen. Und wir erinnern uns, dass ein normaler Operator genau dann unitär ist, wenn sein Spektrum eine Teilmenge des Einheitskreises ist. sind, insbesondere auf dem Einheitskreis liegen. Und wir erinnern uns, dass ein normaler Operator genau dann unitär ist, wenn sein Spektrum eine Teilmenge des Einheitskreises ist.
Nun ist allerdings für einen unitären Operator  , das heißt, es ist unmöglich, aus der Aufgabenstellung Informationen über B zu bekommen. , das heißt, es ist unmöglich, aus der Aufgabenstellung Informationen über B zu bekommen.
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 23. Jul 2017 19:02 Titel: index_razor Verfasst am: 23. Jul 2017 19:02 Titel: |
 |
|
| Bubor hat Folgendes geschrieben: | Ich lade einfach mal die gesamte Aufgabenstellung hoch.
Die anderen beiden Aufgaben beziehen sich nur auf beweisen von Kommutatorrelation, nichts schweres. Und die andere ist auch nur mit einem gegeben Zustand eines Wasserstoff Elektrons rechnen. Auch nichts schweres. Alle Aufgaben sind auch unabhängig voneinander. |
Also, entweder entgeht mir hier etwas oder die Aufgabe ergibt, so wie sie gestellt ist, keinen Sinn. Es ist zwar nicht schwer irgendwelche Lösungen zu finden. Aber diese sind nicht eindeutig und führen im allgemeinen nicht auf dasselbe Spektrum von H. (Zwei, für die H nicht dasselbe Spektrum hat, habe ich schon angegeben.)
Ich denke ohne weitere Voraussetzungen an A und B ist da nicht viel zu machen. Aber, wie gesagt, vielleicht entgeht mir hier irgendwas. Ich denke nochmal drüber nach.
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 23. Jul 2017 19:10 Titel: index_razor Verfasst am: 23. Jul 2017 19:10 Titel: |
 |
|
| APWBDumbledore hat Folgendes geschrieben: |
Erstmal folgt aus den Angaben überhaupt nicht, dass A und B überhaupt unitär diagonalisierbar sind. |
Das muß man m.E. auch gar nicht folgern, d.h. ich könnte mir auch vorstellen, daß es Lösungen gibt, wenn das gar nicht der Fall ist, und A und B irgendwelche windschiefen Eigenbasen haben. Oder ist das ausgeschlossen? Die Selbstadjungiertheit von H wäre ja zumindest nicht betroffen.
|
|
 |
Bubor
Anmeldungsdatum: 24.09.2016
Beiträge: 39
|
 Bubor Verfasst am: 23. Jul 2017 21:24 Titel: Bubor Verfasst am: 23. Jul 2017 21:24 Titel: |
 |
|
@index_razor: Ich wäre deiner Meinung aber kenne mich selbst noch nicht genügend damit aus. Wäre schön wenn APWBDumbledore das näher erläutern könnte
Mir erschien es Anfangs eben auch eigenartig aber ich dachte mir, wenn so eine Aufgabe in der Prüfung dran kam dann werde die sich schon etwas gedacht haben und es schauen ja bei der Erstellung der Prüfung eigentlich mehrere Menschen drauf.
Also fassen wir zusammen das die Aufgabe mit gegeben Mitteln nicht Lösbar ist.
Eine frage am Rande, wie würdet ihr die Aufgabe stellen?
|
|
 |
APWBDumbledore
Gast
|
 APWBDumbledore Verfasst am: 23. Jul 2017 22:36 Titel: APWBDumbledore Verfasst am: 23. Jul 2017 22:36 Titel: |
 |
|
| Bubor hat Folgendes geschrieben: | @index_razor: Ich wäre deiner Meinung aber kenne mich selbst noch nicht genügend damit aus. Wäre schön wenn APWBDumbledore das näher erläutern könnte
|
Klar, mache ich gerne. Was genau möchtest du genauer erläutert haben?
@index_razor: Was meinst du mit "windschiefen Eigenbasen"? Ich kenne windschief nur als Lagebezeichnung für Geraden, die sich weder schneiden, noch parallel zueinander sind.
Also es ist zumindest klar, dass sich A und B, wenn sie denn beide diagonalisierbar sind, in einer gemeinsamen Transformation diagonalisieren lassen, da sie kommutieren. Die Frage ist nur, ob das mit einer unitären Transformation möglich ist.
Allerdings glaube ich bei genauerem Nachdenken, dass zumindest die Diagonalisierbarkeit automatisch folgt. Man könnte von der Jordan-Normalform ausgehen. Dann beachtet man, dass die m-te Potenz eines Jordanblocks  folgendermaßen aussieht: folgendermaßen aussieht:  auf der Hauptdiagonale, auf der Hauptdiagonale,  auf der 1. Nebendiagonale, usw., und 1 auf der m-ten Nebendiagonale (insofern es die aufgrund der Größe des Kästchens gibt). Angenommen, auf der 1. Nebendiagonale, usw., und 1 auf der m-ten Nebendiagonale (insofern es die aufgrund der Größe des Kästchens gibt). Angenommen, 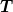 ist die Transformation, die A in die Jordan-Normalform bringt, d.h. ist die Transformation, die A in die Jordan-Normalform bringt, d.h.  , dann muss , dann muss ^3 = J_{\lambda_1 , n_{1,1}}^3 \oplus \dots) , und das kann nur erfüllt sein, wenn alle Jordankästchen die Größe 1 haben, also wenn A diagonalisierbar ist. Ich hoffe, in dem Argument ist kein Fehler. , und das kann nur erfüllt sein, wenn alle Jordankästchen die Größe 1 haben, also wenn A diagonalisierbar ist. Ich hoffe, in dem Argument ist kein Fehler.
Jetzt ist die Frage, was passiert, wenn die Transformation nicht unitär ist. Auf jeden Fall kann man normale A und B finden, die dasselbe leisten. Für ) und und  funktioniert das. Aber leider müssen diese Operatoren nicht simultan diagonalisierbar sein. funktioniert das. Aber leider müssen diese Operatoren nicht simultan diagonalisierbar sein.
Eine Frage war ja zumindest, ob die Operatoren unitär sind. Und die Antwort darauf hängt genau davon ab, ob die Diagonalisierung durch eine unitäre Transformation realisiert ist oder nicht.
|
|
 |
APWBDumbledore
Gast
|
 APWBDumbledore Verfasst am: 23. Jul 2017 23:30 Titel: APWBDumbledore Verfasst am: 23. Jul 2017 23:30 Titel: |
 |
|
Ah, jetzt verstehe ich auch, was index_razor meint mit: "müssen nicht das Spektrum von H liefern".
Das Problem ist, dass, wenn A durch eine Transformation T als Diagonalmatrix  dargestellt wird, nicht automatisch dargestellt wird, nicht automatisch  durch T als durch T als  dargestellt wird. Das ist nur der Fall, wenn die Transformation unitär ist, da im allgemeinen dargestellt wird. Das ist nur der Fall, wenn die Transformation unitär ist, da im allgemeinen ^\dagger \neq T) ist. ist.
|
|
 |
Bubor
Anmeldungsdatum: 24.09.2016
Beiträge: 39
|
 Bubor Verfasst am: 24. Jul 2017 18:49 Titel: Bubor Verfasst am: 24. Jul 2017 18:49 Titel: |
 |
|
Ich habe das so verstanden (was index_razor mit den windschiefen Basen gemeint hat), das die Operatoren in keinster weiße voneinander abhängen. Verstehe ich das richtig?
Aber jetzt nocheinmal einer blöde frage, in deinem Falle ist  ) eine symmetrische Matrix in voraussetzung das das A quadratisch ist. Demnach ist doch auch der Operator A' diagonalisierbar und ich weiß das es Eigenwerte eine symmetrische Matrix in voraussetzung das das A quadratisch ist. Demnach ist doch auch der Operator A' diagonalisierbar und ich weiß das es Eigenwerte 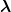 existieren. existieren.
Ich wüsste ja dann auch, das gilt: ^{\dagger} ) ist. ist.
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 24. Jul 2017 19:20 Titel: index_razor Verfasst am: 24. Jul 2017 19:20 Titel: |
 |
|
| APWBDumbledore hat Folgendes geschrieben: |
@index_razor: Was meinst du mit "windschiefen Eigenbasen"?
|
Ich wollte damit nur ausdrücken, daß ich keinen Grund wüßte, warum die Eigenräume von A (oder B) orthogonal zueinander stehen müssen.
|
|
 |
APWBDumbledore
Gast
|
 APWBDumbledore Verfasst am: 25. Jul 2017 19:35 Titel: APWBDumbledore Verfasst am: 25. Jul 2017 19:35 Titel: |
 |
|
| Bubor hat Folgendes geschrieben: |
Aber jetzt nocheinmal einer blöde frage, in deinem Falle ist  ) eine symmetrische Matrix in voraussetzung das das A quadratisch ist. Demnach ist doch auch der Operator A' diagonalisierbar und ich weiß das es Eigenwerte eine symmetrische Matrix in voraussetzung das das A quadratisch ist. Demnach ist doch auch der Operator A' diagonalisierbar und ich weiß das es Eigenwerte 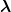 existieren. existieren.
Ich wüsste ja dann auch, das gilt: ^{\dagger} ) ist. ist. |
A ist quadratisch.  (Nur für quadratische Matrizen kann man A², A³ hinschreiben, nur für quadratische Matrizen kann man Eigenwerte diskutieren, und nur quadratische Matrizen sind für die QM relevant) (Nur für quadratische Matrizen kann man A², A³ hinschreiben, nur für quadratische Matrizen kann man Eigenwerte diskutieren, und nur quadratische Matrizen sind für die QM relevant)
A' ist in jedem Fall symmetrisch (im Sinne von konjugiert symmetrisch, also hermitesch), auch wenn A es nicht ist.
Deine letzte Formel ist keine Gleichung, nur ein Term. Falls du schreiben wolltest: ^\dagger = A') , so ist das allerdings falsch. Dafür müsste A' unitär sein, nicht symmetrisch (und es gibt nur sehr wenige Operatoren, die beides sind... das sind genau die, die eine Orthonormalbasis zu Eigenwerten +1 und -1 haben, weil das die Schnittmenge des Einheitskreises, also der Menge, in der unitäre Operatoren ihr Spektrum haben, und der reellen Achse, also der Menge, in der symmetrische Operatoren ihr Spektrum haben, ist). , so ist das allerdings falsch. Dafür müsste A' unitär sein, nicht symmetrisch (und es gibt nur sehr wenige Operatoren, die beides sind... das sind genau die, die eine Orthonormalbasis zu Eigenwerten +1 und -1 haben, weil das die Schnittmenge des Einheitskreises, also der Menge, in der unitäre Operatoren ihr Spektrum haben, und der reellen Achse, also der Menge, in der symmetrische Operatoren ihr Spektrum haben, ist).
|
|
 |
APWBDumbledore
Gast
|
 APWBDumbledore Verfasst am: 25. Jul 2017 19:38 Titel: APWBDumbledore Verfasst am: 25. Jul 2017 19:38 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | APWBDumbledore hat Folgendes geschrieben: |
@index_razor: Was meinst du mit "windschiefen Eigenbasen"?
|
Ich wollte damit nur ausdrücken, daß ich keinen Grund wüßte, warum die Eigenräume von A (oder B) orthogonal zueinander stehen müssen. |
Ah, okay. Die Aufgabenstellung lässt das natürlich zu, aber ich glaube nicht, dass man in diesen Fällen das Spekrum von H mit den Spektra von A und B in Verbindung bringen kann.
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 25. Jul 2017 20:17 Titel: index_razor Verfasst am: 25. Jul 2017 20:17 Titel: |
 |
|
| APWBDumbledore hat Folgendes geschrieben: |
Ah, okay. Die Aufgabenstellung lässt das natürlich zu, aber ich glaube nicht, dass man in diesen Fällen das Spekrum von H mit den Spektra von A und B in Verbindung bringen kann. |
Das wird ja auch nicht verlangt. Aber ich glaube eigentlich auch, daß man A und B als unitär diagonalisierbar voraussetzen soll. Vielleicht sollten wir mal zu diesem Fall zurückkehren. Ich denke so kann man die Aufgabe vielleicht einigermaßen sinnvoll bearbeiten.
|
|
 |
APWBDumbledore
Gast
|
 APWBDumbledore Verfasst am: 25. Jul 2017 20:25 Titel: APWBDumbledore Verfasst am: 25. Jul 2017 20:25 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | APWBDumbledore hat Folgendes geschrieben: |
Ah, okay. Die Aufgabenstellung lässt das natürlich zu, aber ich glaube nicht, dass man in diesen Fällen das Spekrum von H mit den Spektra von A und B in Verbindung bringen kann. |
Das wird ja auch nicht verlangt. Aber ich glaube eigentlich auch, daß man A und B als unitär diagonalisierbar voraussetzen soll. Vielleicht sollten wir mal zu diesem Fall zurückkehren. Ich denke so kann man die Aufgabe vielleicht einigermaßen sinnvoll bearbeiten. |
Ja, das denke ich auch. 
|
|
 |
Bubor
Anmeldungsdatum: 24.09.2016
Beiträge: 39
|
 Bubor Verfasst am: 26. Jul 2017 20:55 Titel: Bubor Verfasst am: 26. Jul 2017 20:55 Titel: |
 |
|
|
Wie würden denn dann ein Ansatz für diese Aufgabe aussehen? Also unter der Vorraussetzung das A und B unitär Diagonalisierbar ist?
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 26. Jul 2017 21:32 Titel: index_razor Verfasst am: 26. Jul 2017 21:32 Titel: |
 |
|
| Bubor hat Folgendes geschrieben: | | Wie würden denn dann ein Ansatz für diese Aufgabe aussehen? Also unter der Vorraussetzung das A und B unitär Diagonalisierbar ist? |
Ich würde damit anfangen zu überlegen, was aus der Vertauschbarkeit der beiden Operatoren folgt.
Du kannst, denke ich, auch von meinen obigen Lösungen ausgehen und die verallgemeinern.
|
|
 |
Bubor
Anmeldungsdatum: 24.09.2016
Beiträge: 39
|
 Bubor Verfasst am: 28. Jul 2017 15:12 Titel: Bubor Verfasst am: 28. Jul 2017 15:12 Titel: |
 |
|
Ahh ok, ja stimmt. Vielen Dank 
|
|
 |
|

















 (Nur für quadratische Matrizen kann man A², A³ hinschreiben, nur für quadratische Matrizen kann man Eigenwerte diskutieren, und nur quadratische Matrizen sind für die QM relevant)
(Nur für quadratische Matrizen kann man A², A³ hinschreiben, nur für quadratische Matrizen kann man Eigenwerte diskutieren, und nur quadratische Matrizen sind für die QM relevant)
