| Autor |
Nachricht |
vektorling
Gast
|
 vektorling Verfasst am: 28. Jun 2014 21:58 Titel: Vektoren als differential Operatoren |
 |
|
Hallo, ich lese grade ein Buch über mathematische Physik und die notation treibt mich in den Wahnsinn. Kann mir jemand den Unterschied zwischen:
 := D_{x} := \sum\limits_{j} [\frac{\partial f}{\partial x^{j}}](p)X^{j})
und
 = \sum\limits_{j} X^{j} \frac{\partial}{\partial x^{j}}|_{p} )
Erklären? Vor allem was soll diese partielle Ableitung wo einfach nur die Ableitung drin steht, ohne das was Abgeleitet werden soll.
Später wird auch noch mal ein Vektorfeld als :
 \frac{\partial}{\partial x^{j}})
Definiert.
Kann mir das jemand mal in normaler Notation erklären?
(Alles spielt sich auf einer Manigfaltigkeit ab)
Gruß |
|
 |
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8583
|
| jh8979 Verfasst am: 28. Jun 2014 22:00 Titel: |
|
|
|
In der zweiten Gleichung fehlt ein f auf der rechten Seite (oder links ist das "(f)" zuviel). |
|
|
vektorling
Gast
|
| vektorling Verfasst am: 28. Jun 2014 22:08 Titel: |
|
|
Bei der zweiten Gleichung muss das f weg.
Gruß |
|
|
Vektorling
Gast
|
| Vektorling Verfasst am: 28. Jun 2014 22:09 Titel: |
|
|
Oh, ja danke  |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8583
|
| jh8979 Verfasst am: 28. Jun 2014 22:10 Titel: Re: Vektoren als differential Operatoren |
|
|
Das hier
ist ein Differentialoperator (der auf Funktionen wirkt), und das hier:
 := D_{x} := \sum\limits_{j} X^{j} \frac{\partial f}{\partial x^{j}}|_{p} )
Ist der Differentialoperator angewandt auf eine Funktion f. |
|
|
Vektorling
Gast
|
| Vektorling Verfasst am: 28. Jun 2014 22:14 Titel: |
|
|
Halt moment, ich hab totalen Quatsch geschrieben. Ich meine den Unterschied zwischen:
:=D_{x}(f):= \sum\limits_{j} [\frac{\partial f}{\partial x^{j}}](p)X^{j})
und
Wieso sind bei einem die Komponenten links und beim anderen rechts??
Gruß |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8583
|
| jh8979 Verfasst am: 28. Jun 2014 22:16 Titel: |
|
|
| Vektorling hat Folgendes geschrieben: |
Wieso sind bei einem die Komponenten links und beim anderen rechts??
|
Das ist egal, da das alles nur Zahlen sind und die vertauschen. |
|
|
vektorling
Gast
|
| vektorling Verfasst am: 28. Jun 2014 22:19 Titel: |
|
|
|
aso hm ok |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8583
|
| jh8979 Verfasst am: 28. Jun 2014 22:22 Titel: |
|
|
Vllt als kleine Ergänzung:
Normalerweise wuerd ich die Komponenten immer links schreiben, da dann keine Ambiguität entsteht ob der Differentialoperator noch auf sie wirken soll (insbesondere wenn es in der Diff-Op.-Schreibweise ohne Funktion die Abgeleitet wird geschrieben wird). |
|
|
Vektorling
Gast
|
| Vektorling Verfasst am: 28. Jun 2014 22:26 Titel: |
|
|
Ja ok, danke ich habs verstanden.  ist ja einfach nur der Basisvektor Koordinatenfrei dargestellt.
Gruß |
|
|
Nobundo
Anmeldungsdatum: 12.03.2014
Beiträge: 168
|
| Nobundo Verfasst am: 28. Jun 2014 22:45 Titel: |
|
|
| Vektorling hat Folgendes geschrieben: | Ja ok, danke ich habs verstanden. ist ja einfach nur der Basisvektor Koordinatenfrei dargestellt.
Gruß |
Die Darstellung ist nicht Koordinatenfrei. Sondern das was du geschrieben hast ist gerade das "j-te Koordinatenfeld" |
|
|
Vektorling
Gast
|
| Vektorling Verfasst am: 29. Jun 2014 14:36 Titel: |
|
|
Ohh, kann mir mal jemand ein Beispiel geben? Auf was wirkt das denn?? Auf eine Skalarfunktion? Oder auf eine Vektorfunktion? Ist das wie der Gradient einer Skalarfunktion? Wenn ich z.B. r(u,v)=(cos u, sin u, v) wie sieht das dann aus?
Gruß |
|
|
Nobundo
Anmeldungsdatum: 12.03.2014
Beiträge: 168
|
| Nobundo Verfasst am: 29. Jun 2014 14:43 Titel: |
|
|
| Vektorling hat Folgendes geschrieben: | Ohh, kann mir mal jemand ein Beispiel geben? Auf was wirkt das denn?? Auf eine Skalarfunktion? Oder auf eine Vektorfunktion? Ist das wie der Gradient einer Skalarfunktion? Wenn ich z.B. r(u,v)=(cos u, sin u, v) wie sieht das dann aus?
Gruß |
Das r(u,v) das du angegeben hast, ist eine Paramtrisierung für einen Zylinder mit Radius 1. In diesem Fall sind die Abletiungen  ,  nach den Koordinaten u,v die Koordinatenfelder. Sie wirken auf skalare Funktionen auf der Mannigfaltigkeit, aber wie gesagt in der Koordinatendarstellung bezüglich u,v. |
|
|
Vektorling
Gast
|
| Vektorling Verfasst am: 29. Jun 2014 14:49 Titel: |
|
|
Hallo, ich meine jetzt als Vektor an einer Manigfaltigkeit.
Gruß |
|
|
Nobundo
Anmeldungsdatum: 12.03.2014
Beiträge: 168
|
| Nobundo Verfasst am: 29. Jun 2014 14:54 Titel: |
|
|
| Vektorling hat Folgendes geschrieben: | Hallo, ich meine jetzt als Vektor an einer Manigfaltigkeit.
Gruß |
Die Tangentialvektoren erhält man in diesem Fall als Ableitungen der Parametrisierung ) bzw ) |
|
|
Vektorling
Gast
|
| Vektorling Verfasst am: 29. Jun 2014 14:54 Titel: |
|
|
Was ist X^{j}? Eine Ableitung? Oder einfach nur eine Komponente.
Gruß |
|
|
Vektorling
Gast
|
| Vektorling Verfasst am: 29. Jun 2014 14:55 Titel: |
|
|
|
Ja dann halt als Vektorfeld. |
|
|
Nobundo
Anmeldungsdatum: 12.03.2014
Beiträge: 168
|
| Nobundo Verfasst am: 29. Jun 2014 15:07 Titel: |
|
|
| Vektorling hat Folgendes geschrieben: | Was ist X^{j}? Eine Ableitung? Oder einfach nur eine Komponente.
Gruß |
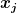 ist die j-te Koordinate deiner Karte/Parametrisierung. Das Vektorfeld  entspricht dann in jedem Punkt dem Tangentialvektor in Richtung  und wirkt auf eine Funktion indem er diese in Richtung 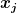ableitet. Meintest du das? |
|
|
Vektorling
Gast
|
| Vektorling Verfasst am: 29. Jun 2014 15:24 Titel: |
|
|
AHH man braucht eine Funktion UND eine Parametrisierung !!! Dann kann man die änderung des Feldes in Richtung z.B. einer Kurve berechnen. Ahh ok, ich wusste nicht ob ich jetzt eine Skalarfunktion oder eine vektorwertige Funktion brauche, das man das auch kombinieren kann daran hab ich gar nicht gedacht.
Ja danke deine Antwort hat geholfen.
Gruß |
|
|
Vektorling
Gast
|
| Vektorling Verfasst am: 29. Jun 2014 15:29 Titel: |
|
|
Ah, das ist doch das gleiche wie wenn man in der Elektrodynamik den Fluss von einem E Feld durch einen Draht berechnet oder?
Gruß |
|
|
Nobundo
Anmeldungsdatum: 12.03.2014
Beiträge: 168
|
| Nobundo Verfasst am: 30. Jun 2014 19:50 Titel: |
|
|
| Vektorling hat Folgendes geschrieben: | Ah, das ist doch das gleiche wie wenn man in der Elektrodynamik den Fluss von einem E Feld durch einen Draht berechnet oder?
Gruß |
Den Zusammenhang sehe ich jetzt nicht direkt, ausser das ein E-Feld auch ein Vektorfeld auf einer Mannigfaltigkeit ist, zb einfach dem R^3.
Kannst du genauer beschreiben wie du das meinst? |
|
|
Vektorling
Gast
|
| Vektorling Verfasst am: 01. Jul 2014 22:34 Titel: |
|
|
Schon ok, Danke für die Hilfe
Gruß |
|
|
|
Registrieren
Login
FAQ
Suchen
