ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3388
|
 ML Verfasst am: 12. Mai 2017 11:41 Titel: FAQ - Induktionsgesetz in integraler Schreibweise, Teil II ML Verfasst am: 12. Mai 2017 11:41 Titel: FAQ - Induktionsgesetz in integraler Schreibweise, Teil II |
 |
|
Experimente
Im folgenden werden zwei Experimente gezeigt, die zeigen, wie das Induktionsgesetz
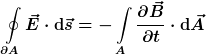
korrekt auf die Experimente "Bewegter Leiterstab im homogenen, zeitlich konstanten Magnetfeld" und "Hering'sches Paradoxon" angewendet wird.
Bewegter Leiterstab im homogenen, zeitlich konstanten Magnetfeld
Der im nebenstehenden Bild skizzierte Messaufbau besteht aus einer ruhenden, elektrisch leitfähigen Schienenanordnung, über die mit der Geschwindigkeit 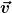 ein Leiterstab gleitet. Die Anordnung befindet sich in einem örtlich und zeitlich konstanten magnetischen Feld mit der Flussdichte ein Leiterstab gleitet. Die Anordnung befindet sich in einem örtlich und zeitlich konstanten magnetischen Feld mit der Flussdichte 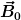 , das durch einen ruhenden Permanentmagneten oder eine ruhende mit Gleichstrom betriebene Spulenanordnung hervorgerufen wird. Die Spannung zwischen den beiden Schienen wird mit einem Voltmeter gemessen. Da der Stromkreis geöffnet ist, fließt kein Strom. , das durch einen ruhenden Permanentmagneten oder eine ruhende mit Gleichstrom betriebene Spulenanordnung hervorgerufen wird. Die Spannung zwischen den beiden Schienen wird mit einem Voltmeter gemessen. Da der Stromkreis geöffnet ist, fließt kein Strom.
 https://upload.wikimedia.org/wikipedia/commons/thumb/3/35/Bewegter_Leiter_im_Feld-Feldlinienbild.svg/512px-Bewegter_Leiter_im_Feld-Feldlinienbild.svg.png https://upload.wikimedia.org/wikipedia/commons/thumb/3/35/Bewegter_Leiter_im_Feld-Feldlinienbild.svg/512px-Bewegter_Leiter_im_Feld-Feldlinienbild.svg.png
Bewegter Leiter im Feld-Feldlinienbild
Es ist bekannt, dass das Voltmeter bei dieser Anordnung
eine Spannung von
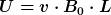
anzeigt.
Irrtümlich wird jedoch häufig behauptet, dass die o. g. (korrekte) Version des Induktionsgesetzes auf diese Anordnung nicht anwendbar sei, da sich der Leiterstab bewege. Dies soll hier widerlegt werden.
Wir berechnen zunächst das Ringintegral über E entlang einer geschlossenen, dem Leiterverlauf folgenden, Kurve. Die Kurve beschreibt einen kompletten Umlauf von der oberen Anschlussklemme des Voltmeters im Uhrzeigersinn laufend über die obere Schiene, den Leiterstab, die untere Schiene und das Messgerät bis zurück zur oberen Anschlussklemme des Voltmeters. Es ergeben sich vier Anteile für das Integral:
- Von der oberen Klemme ausgehend entlang der Schiene (innerhalb des Materials) bis zur oberen Kontaktfläche des sich bewegenden Leiterstabs: Da hier überall eine E-Feldstärke von null herrscht, ist dieser Anteil des Integrals gleich null.
- Von der Kontaktfläche des Leiterstabes bis zur unteren Kontaktfläche des Leiterstabes: Da im Leiterstab keine stromtreibende Kraft wirkt, gilt
 = 0) , also , also 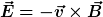 . . 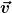 ist hierbei die Geschwindigkeit des Leiterstabes. Die elektrische Feldstärke zeigt, wie im Bild dargestellt, "von oben nach unten", und integriert ergibt sich der Wert ist hierbei die Geschwindigkeit des Leiterstabes. Die elektrische Feldstärke zeigt, wie im Bild dargestellt, "von oben nach unten", und integriert ergibt sich der Wert 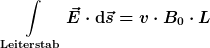 . .
- Von der oberen Kontaktfläche des sich bewegenden Leiterstabs bis zur unteren Anschlussklemme des Voltmeters (innerhalb des Schienenmaterials verlaufend): Da hier überall eine E-Feldstärke von null herrscht, ist dieser Anteil des Integrals gleich null.
- Von der unteren Anschlussklemme des Voltmeters bis zur oberen Anschlussklemme des Voltmeters: Hier ergibt sich der Wert -U, also gerade der Wert, den das Voltmeter anzeigt. Das negative Vorzeichen kommt daher, dass wir entgegen der Richtung des Spannungspfeiles integrieren.
Die rechte Seite des Induktionsgesetzes ergibt:
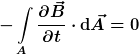 , ,
da voraussetzungsgemäß 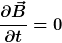 gilt. Es sei angemerkt, dass aus diesem Grund das Experiment eigentlich gar nicht zum Thema "Elektromagnetische Induktion" passt, sondern viel eher zum Thema "Elektrostatik". gilt. Es sei angemerkt, dass aus diesem Grund das Experiment eigentlich gar nicht zum Thema "Elektromagnetische Induktion" passt, sondern viel eher zum Thema "Elektrostatik".
Insgesamt ergibt sich also:
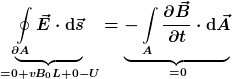
Dieses Ergebnis deckt sich hervorragend mit dem Messergebnis 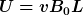 . .
Fehlerhinweis: Viele Menschen denken, dass innerhalb des bewegten Leiterstabes ein E-Feld von null herrsche, da schließlich ein guter Leiter vorliege, und kommen dann zum Ergebnis, dass die (korrekte) Version des Induktionsgesetzes falsch sein müsse.
Dabei verwechseln sie jedoch die Bezugssysteme:
- Betrachtet aus dem gewählte Bezugssystem, für den der Leiterstab sich mit der Geschwindigkeit
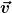 bewegt und für das das Voltmeter ruht (Laborsystem), ist die Feldstärke im Leiterstab ungleich null. Nur in einem Bezugssystem, in dem der Leiterstab ruht, gilt eine Feldstärke von null. Das bedeutet, ein "mitbewegter" Beobachter würde eine Feldstärke von E'=0 messen. bewegt und für das das Voltmeter ruht (Laborsystem), ist die Feldstärke im Leiterstab ungleich null. Nur in einem Bezugssystem, in dem der Leiterstab ruht, gilt eine Feldstärke von null. Das bedeutet, ein "mitbewegter" Beobachter würde eine Feldstärke von E'=0 messen.
- Befürworter des falschen Induktionsgesetzes
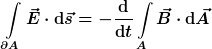
meinen in aller Regel die Näherung des Induktionsgesetzes
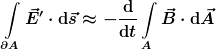 , ,
sie vergessen aber den kleinen Strich am E-Feld.
Hering'sches Paradoxon
Ebenfalls sehr lehrreich für die korrekte Anwendung des Induktionsgesetzes ist das "Hering'sche Paradoxon".
 https://upload.wikimedia.org/wikipedia/commons/thumb/b/b8/Induktion_ohne_Spannungsanzeige.svg/512px-Induktion_ohne_Spannungsanzeige.svg.png https://upload.wikimedia.org/wikipedia/commons/thumb/b/b8/Induktion_ohne_Spannungsanzeige.svg/512px-Induktion_ohne_Spannungsanzeige.svg.png
Induktion ohne Spannungsanzeige
Beim Herin'schen Paradoxon wird ein elektrisch leitfähiger Permanentmagnet entsprechend dem obenstehenden Bild mit der Geschwindigkeit  in eine offene Leiterschleifenanordnung hineinbewegt. Über eine Anordnung mit elektrisch leitfähigen Rollen verbindet der Permanentmagnet dabei die beiden Enden der Leiterschleifenanordnung. in eine offene Leiterschleifenanordnung hineinbewegt. Über eine Anordnung mit elektrisch leitfähigen Rollen verbindet der Permanentmagnet dabei die beiden Enden der Leiterschleifenanordnung.
Die Randlinie 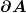 soll im Bereich der (ruhenden) Leiterschleife dem Leiter folgen und im Bereich des Permanentmagneten eine ruhende, direkte Verbindung zwischen den beiden Rollen herstellen. Das bedeutet, dass die Geschwindigkeit soll im Bereich der (ruhenden) Leiterschleife dem Leiter folgen und im Bereich des Permanentmagneten eine ruhende, direkte Verbindung zwischen den beiden Rollen herstellen. Das bedeutet, dass die Geschwindigkeit 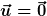 der Flächenrandlinie sich von der Geschwindigkeit der Flächenrandlinie sich von der Geschwindigkeit 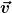 des Permanentmagneten unterscheidet. Als Fläche des Permanentmagneten unterscheidet. Als Fläche  kann jede beliebige orientierte, von kann jede beliebige orientierte, von 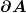 berandete Fläche angenommen werden. berandete Fläche angenommen werden.
Das Experiment wird von vielen als paradox empfunden, da der magnetische Fluss durch die Fläche  sich zwar mit der Zeit ändert, das Voltmeter aber zu keinem Zeitpunkt eine Spannung anzeigt. sich zwar mit der Zeit ändert, das Voltmeter aber zu keinem Zeitpunkt eine Spannung anzeigt.
Dabei ist aus dem betrachteten Bezugssystem gesehen das Ringintegral 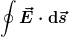 über die elektrische Feldstärke tatsächlich ungleich null. Das zugehörige E-Feld ist bloß an einer anderen Stelle zu finden als erwartet. Es befindet sich nicht im Voltmeter, sondern vielmehr im Magneten. über die elektrische Feldstärke tatsächlich ungleich null. Das zugehörige E-Feld ist bloß an einer anderen Stelle zu finden als erwartet. Es befindet sich nicht im Voltmeter, sondern vielmehr im Magneten.
Zur Klärung berechnen wir wie im ersten Beispiel das Ringintegral über E entlang einer geschlossenen Kurve. Als Kurve wählen wir (im Uhrzeigersinn verlaufend) einen kompletten Umlauf ausgehend von der oberen Anschlussklemme des Voltmeters über die Zuleitung zur oberen Rolle, weiter durch den sich bewegenden Permanentmagneten, die Zuleitung zur unteren Rolle, die unteren Anschlussklemmen und das Voltmeter zurück zu den oberen Anschlussklemmen des Voltmeters.
Es ergeben sich drei Anteile:
- In allen (ruhenden) Zuleitungen ist das E-Feld gleich null.
- Im Voltmeter ist das E-Feld ebenfalls gleich null.
- Im Permanentmagnet herrscht jedoch ein E-Feld von
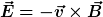 . Es zeigt im Beispiel "von unten nach oben". . Es zeigt im Beispiel "von unten nach oben".
Grund für die Existenz des E-Feldes ist -- wie im oberen Beispiel --, dass sich dort ein Leiter (der Permanentmagnet) im B-Feld bewegt. Da kein Strom fließt, herrscht ein Kräftegleichgewicht von elektrischer Kraft und Lorentzkraft, so dass gilt:  = \vec 0) , also , also 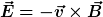 . .
Aufgrund des angedeuteten E-Feldverlaufs ergibt sich für die linke Seite des Induktionsgesetzes:
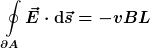
Die rechte Seite des Induktionsgesetzes ergibt ebenfalls:
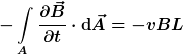 , ,
Damit ist gezeigt, dass das Induktionsgesetz auch auf dieses Beispiel anwendbar ist.
Sehr wenig intuitiv ist bei diesem Beispiel die Tatsache, dass im bewegten Permanentmagnet ein E-Feld von 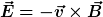 herrscht und nicht -- wie man intuitiv erwarten könnte -- ein E-Feld von null. Hinter der irrtümlichen Vorstellung von E=0 steckt die intuitiv naheliegende, aber physikalisch unsinnige Begründung, dass sich der Magnet ja gar nicht "relativ zum Magnetfeld" bewege. Die Bewegung "relativ zum Magnetfeld" ist in der Elektrodynamik jedoch kein sinnvoller Begriff, wie in einer anderen FAQ ausführlich erläutert wurde. Die Denkweise geht vielmehr folgendermaßen: 1) ein Leiter (=Magnet) bewegt sich und 2) am Ort der Bewegung herrscht ein Magnetfeld. Folgerung: Der Leiter bewegt sich im Magnetfeld. herrscht und nicht -- wie man intuitiv erwarten könnte -- ein E-Feld von null. Hinter der irrtümlichen Vorstellung von E=0 steckt die intuitiv naheliegende, aber physikalisch unsinnige Begründung, dass sich der Magnet ja gar nicht "relativ zum Magnetfeld" bewege. Die Bewegung "relativ zum Magnetfeld" ist in der Elektrodynamik jedoch kein sinnvoller Begriff, wie in einer anderen FAQ ausführlich erläutert wurde. Die Denkweise geht vielmehr folgendermaßen: 1) ein Leiter (=Magnet) bewegt sich und 2) am Ort der Bewegung herrscht ein Magnetfeld. Folgerung: Der Leiter bewegt sich im Magnetfeld.
Überraschenderweise wird das Experiment nur dann als paradox empfunden, wenn man es (wie hier vorliegend) aus einem Bezugssystem heraus beschreibt, in dem sich der Magnet bewegt. Betrachtet man das Experiment hingegen aus einem Bezugssystem, in dem der Magnet ruht, dann ist es für die meisten Leute ausgesprochen intuitiv und leicht verständlich. Denn was sieht ein auf dem Magneten sitzender Beobachter: Er sieht ein paar Drähte und ein Voltmeter, die sich im feldfreien Raum bewegen. Aus diesem Blickwinkel betrachtet ist intuitiv sofort klar, weshalb das Voltmeter eine Spannung von 0 anzeigt. Denn bei dem Experiment passiert überhaupt nichts, was eine Spannung verursachen könnte. |
|
















