ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3388
|
 ML Verfasst am: 29. Apr 2017 16:05 Titel: FAQ - Induktionsgesetz in integraler Schreibweise ML Verfasst am: 29. Apr 2017 16:05 Titel: FAQ - Induktionsgesetz in integraler Schreibweise |
 |
|
Problemstellung
Obwohl seit mehr als 100 Jahren bekannt ist, dass die Maxwellgleichungen mit der speziellen Relativitätstheorie verträglich sind (Albert Einstein, "Zur Elektrodynamik bewegter Körper", 1905) und ihre differentielle Schreibweise allgemein akzeptiert ist, taucht in Diskussionen zur elektromagnetischen Induktion immer wieder die Frage auf, wie das Induktionsgesetz in integraler Schreibeweise korrekt notiert wird.
Je nach Lehrwerk werden vier verschiedene Schreibweisen angeboten:
-

-
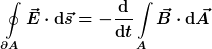 und und
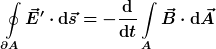
 \cdot \mathrm{d}\vec s = -\frac{\mathrm{d}}{\mathrm{d} t} \int\limits_{A}\vec B \cdot \mathrm{d}\vec A)
Hinsichtlich der differentiellen Schreibweise sind sich fast alle Autoren (inkl. Maxwell und Einstein) einig, dass das Induktionsgesetz korrekterweise durch die Gleichung:
- 1)
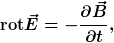
beschrieben wird. Nur wenige Lehrbuchautoren notieren das Induktionsgesetz irrtümlich als
- 2)
, )
verteidigen es aber gegenüber Kritik umso vehementer und nennen diese Form des Induktionsgesetzes das "Induktionsgesetz in seiner allgemeinsten Form".
Die folgende Darstellung stellt klar, welche Schreibweisen richtig sind und in welchem Verhältnis die anderen Gleichungen dazu stehen.
In den Rechnungen wird zunächst davon ausgegangen, dass die Schreibweise 1) und die damit äquivalenten Schreibweisen a) und d) die korrekten Versionen des Induktionsgesetzes sind. Später wird demonstriert, dass die Version 2) und die damit äquivalente integrale Formulierung b) im groben Widerspruch zu einfachen, im Klassenraum leicht durchzuführenden Schulexperimenten steht.
Die Version c) des Induktionsgesetzes nimmt eine Sonderstellung ein. Sie ist nicht ganz falsch, aber auch nicht ganz richtig. Es handelt sich vielmehr um eine Näherung, die für kleine Geschwindigkeiten 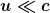 des jeweiligen Linienelements des jeweiligen Linienelements 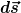 korrekt ist. Insofern lässt sie sich nicht durch einfache Experimente im Klassenraum widerlegen, sondern nur durch theoretische Überlegungen oder durch Experimente, bei denen relativistische Geschwindigkeiten auftreten. korrekt ist. Insofern lässt sie sich nicht durch einfache Experimente im Klassenraum widerlegen, sondern nur durch theoretische Überlegungen oder durch Experimente, bei denen relativistische Geschwindigkeiten auftreten.
Der kleine Strich bei der elektrischen Feldstärke bedeutet, dass die elektrische Feldstärke 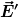 nicht -- wie sonst allgemein üblich -- aus dem für alle Größen identisch gewählten Inertialsystem (Bezugssystem) heraus gemessen wird, sondern jeweils von einem Beobachter gemessen wird, für den das jeweilige Linienelement nicht -- wie sonst allgemein üblich -- aus dem für alle Größen identisch gewählten Inertialsystem (Bezugssystem) heraus gemessen wird, sondern jeweils von einem Beobachter gemessen wird, für den das jeweilige Linienelement 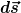 ruht. ruht.
Korrekte Interpretation der Gleichungen und Übergang in die integrale Schreibweise
Für eine korrekte Interpretation der integralen Gleichungen ist es wichtig zu verstehen, dass das Induktionsgesetz per se nur Aussagen über Felder -- die Vektorfelder ) und und ) -- trifft, aber keine Aussagen über Leiterdrähte, die Bewegung von Materie oder über sonstige Kopplungen an Materie trifft. -- trifft, aber keine Aussagen über Leiterdrähte, die Bewegung von Materie oder über sonstige Kopplungen an Materie trifft.
Dies wird besonders deutlich an der differentiellen Schreibweise:
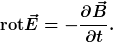
Diese Gleichung besagt, dass die zeitliche Änderung der magnetischen Flussdichte immer einhergeht mit einer lokalen Wirbelstärke der elektrischen Feldstärke. Man kann sich diese Gleichung anschaulich ungefähr so vorstellen, dass um die Feldlinien des Vektorfeldes 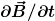 herum kleine geschlossene E-Feldlinien existieren, die sich mit dem restlichen E-Feld der Anordnung überlagern. herum kleine geschlossene E-Feldlinien existieren, die sich mit dem restlichen E-Feld der Anordnung überlagern.
Zur Überführung in die integrale Schreibweise definiert man eine beliebige orientierte Fläche  mit der Randlinie mit der Randlinie 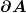 und integriert formal beide Seiten des Induktionsgesetzes über diese Fläche. Es ergibt sich zunächst: und integriert formal beide Seiten des Induktionsgesetzes über diese Fläche. Es ergibt sich zunächst:
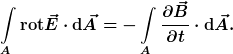
Die linke Seite kann mithilfe des Satzes von Stokes noch weiter umformen. Dieser Satz besagt anschaulich, dass sich bei einer Flächenintegration über die "E-Feld-Kringel" die E-Felder im Inneren der Fläche "wegen Gegenverkehrs" gegeneinander aufheben, so dass nur das Ringintegral über E entlang der Randlinie übrigbleibt. Dies wird im folgenden Link veranschaulicht:
 http://commons.wikimedia.org/wiki/File%3AStokes-patch.png http://commons.wikimedia.org/wiki/File%3AStokes-patch.png
Mithilfe des Satzes von Stokes ergibt sich folglich:
a) 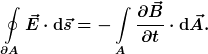
Durch diese Herleitung ist gezeigt, dass die Version des Induktionsgesetzes in der Schreibweise a) die gleichen Aussagen trifft wie von Maxwell und Einstein vorgeschlagene Version 1) der differentiellen Schreibweise, die hier als korrekt bezeichnet wird.
Wie H. Flanders im Artikel "Differential under the integral sign" (American Mathematical Monthly (6), S. 615-627) zeigt, gilt für beliebige gutmütige Vektorfelder 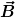 die folgende Gleichung: die folgende Gleichung:
 \cdot \mathrm{d}\vec{s} + \int \limits_A (\nabla \cdot \vec{B}) \cdot \vec{u} \cdot \mathrm{d}\vec{A}.)
Da laut einer Maxwellgleichung die Divergenz des B-Feldes immer gleich null ist (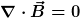 , es gibt keine magnetischen Monopole), trifft für die magn. Flussdichte eine Vereinfachung zu: , es gibt keine magnetischen Monopole), trifft für die magn. Flussdichte eine Vereinfachung zu:
 \cdot \mathrm{d}\vec{s})
In der Umformung wurde 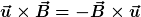 verwendet. Setzt man diese Gleichung in das korrekte Induktionsgesetz nach Schreibweise a) ein und formt ein wenig um, so ergibt sich: verwendet. Setzt man diese Gleichung in das korrekte Induktionsgesetz nach Schreibweise a) ein und formt ein wenig um, so ergibt sich:
d)  \cdot \mathrm{d}\vec s = -\frac{\mathrm{d}}{\mathrm{d}t} \int \limits_A \vec B \cdot\mathrm{d} \vec A.)
Dies ist jedoch gerade die Schreibweise d) des Induktionsgesetzes, die aus diesem Grund ebenfalls als korrekt angesprochen wird.
Bei der Schreibweise d) ist zu beachten, dass 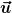 jeweils die Geschwindigkeit eines kleinen Flächenelementes jeweils die Geschwindigkeit eines kleinen Flächenelementes 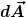 bzw. eines kleinen Elementes bzw. eines kleinen Elementes 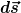 der Randlinie der Fläche ist. der Randlinie der Fläche ist.
Es geht hierbei nicht um irgendwelche Drähte oder andere Leiter, denn in der mathematischen Herleitung sind diese an keiner Stelle eingeführt worden. Der Unterschied zwischen einer Linie und einem Drahtstück besteht darin, dass die Linie ein Objekt ist, das nur in unserer Vorstellung existiert, während Drähte etwas Echtes sind. Bewegungen einer Linie können die Vektorfelder nicht beeinflussen. Das Einfügen eines Drahtstückes und seine Bewegung vermögen dies aber selbstverständlich schon. Im Induktionsgesetz sind nur Linien notiert, nicht Drähte oder sonstige Leiter.
Wählt man in der korrekten Formulierung nach d) die Geschwindigkeit der Randlinie zu 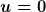 , so ergibt sich daraus die Formulierung b): , so ergibt sich daraus die Formulierung b):
b) 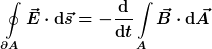
Die Formulierung nach b) ist also offensichtlich ein Spezialfall des Induktionsgesetzes, der immer dann gilt, wenn die Randlinie 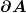 als ruhend angenommen wird oder wenn das Integral als ruhend angenommen wird oder wenn das Integral  \cdot \mathrm{d}\vec s) aus anderen Gründen verschwindet. aus anderen Gründen verschwindet.
Es sei angemerkt, dass man die Formulierung b) in integraler Schreibweise von vielen als äquivalent zur Formulierung 2) in differentieller Schreibweise ansehen wird. Unklar ist dabei jedoch, welchem Objekt formal gesehen die Geschwindigkeit zugeordnet wird. Da die Gleichung 2) die Physik ohnehin nicht korrekt wiedergibt, muss diese Frage für den Zweck dieser FAQ nicht weiter vertieft werden.
Setzt man in der korrekten Formulierung nach d) die Näherung 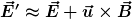 der Lorentztransformation für die elektrische Feldstärke ein, so ergibt sich daraus die Formulierung nach c): der Lorentztransformation für die elektrische Feldstärke ein, so ergibt sich daraus die Formulierung nach c):
c) 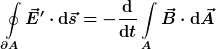 und und
Da man ausgehend von der korrekten Formulierung eine Näherung eingesetzt hat, ist diese Gleichung ebenfalls nur eine Näherung, die für relativistisch kleine Geschwindigkeiten der Randlinie 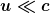 gilt. Es sei angemerkt, dass diese Version ausnahmsweise relativistisch exakt ist, sofern entlang der bewegten Bereiche der Randlinie die Feldstärke E'=0 herrscht. gilt. Es sei angemerkt, dass diese Version ausnahmsweise relativistisch exakt ist, sofern entlang der bewegten Bereiche der Randlinie die Feldstärke E'=0 herrscht.
Experimente
... wird fortgesetzt
Zuletzt bearbeitet von ML am 01. Mai 2017 13:47, insgesamt 3-mal bearbeitet |
|
















